基于观测器的不确定广义系统的时滞依赖无源控制

范桂英,卢永红,肖润梅

（山西大同大学数学与统计学院，山西大同037009）

无源性概念自引入以来，过去的几十年中许多学者对不确定性时滞系统的无源问题做了研究,时滞系统的研究已成为热点并且涌现出许多的研究成果[1-4]。文献[5]针对不确定广义系统研究了其时滞依赖鲁棒镇定问题，文献[6]针对线性系统研究了其基于观测器的时滞依赖无源控制问题，文献[7]针对时滞广义系统的研究了其基于观测器的时滞依赖无源控制，但对控制输入含有时滞同时参数也带有不确定性的广义系统,考虑其观测器设置的时滞依赖无源控制的研究并未见。

1 预备知识

给出如下的不确定时滞广义系统

其中u(t)∈Rn，x(t)∈Rn，z(t)∈Rn分别是控制输入、状态向量、被调输出，w(t)∈Rn是属于L2[0,∞)空间的干扰输入，A，A1，B，B1，C，C1，D，D1，C2分别是适当维数的常数矩阵， ，ΔA1，ΔB，ΔB1，ΔC，ΔC1，ΔD，ΔBw和ΔDw分别是不确定性参数且依次具有形式EiFi(t)Hi，其中Ei，Hi是已知的适当维数的常数矩阵。是lebesgue 可测的。时滞函数d(t)是时变时滞的并满足0 ≤d(t)<

定义1对于系统(1)的自治系统，如果存在一个非负定函数V(x(t)),一个正数η，使得无源不等式V̇(x(t))-2wT(t)z(t)+2ηwT(t)w(t)<0 对于任意的输人信号w(t)和所有容许的不确定性成立, 则称系统(1)的自治系统是无源的，当不等式严格成立时,系统称为严格无源的。

引理1(Schur 补) 对于给定的对称矩阵其中则以下三个条件是等价的

(I)S<0；

引理2对于任意正定对称矩阵M∈Rn×m，标量γ>0 向量函数ω[0γ]→Rn，则下式成立

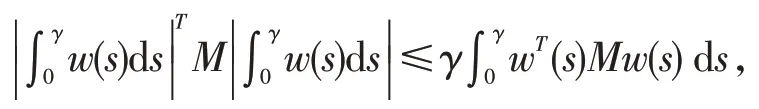
考虑如下基于观测器的控制器

其中，ξ(t)∈Rn为状态x的估计；K∈Rn×q为观测增益矩阵。

令e(t)=x(t)-ξ(t),则由系统(1)与误差动态方程组成的增广闭环系统为

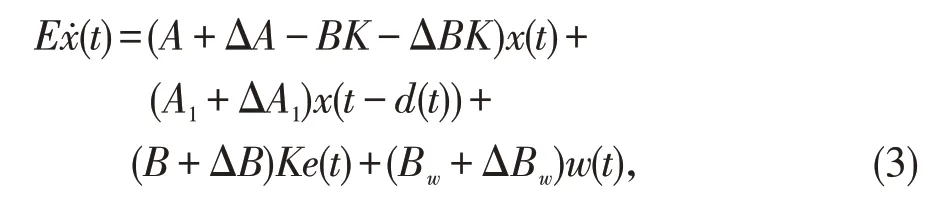
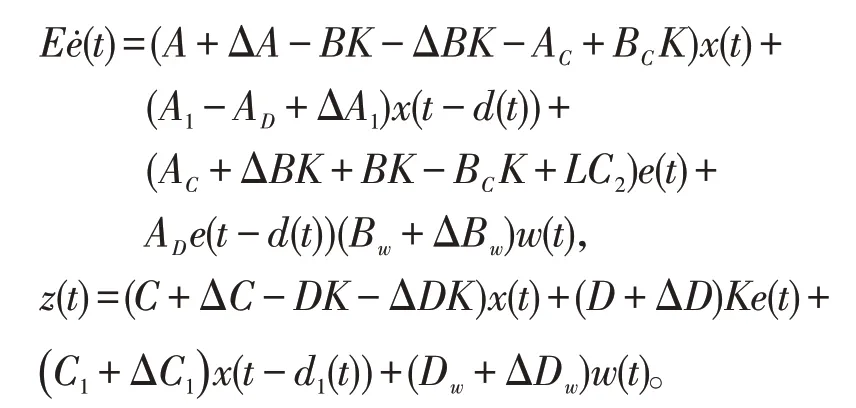
2 主要结论

定理1若存在可逆矩阵P1,P2,S1,S2,R1,R2,矩阵K,L使得满足

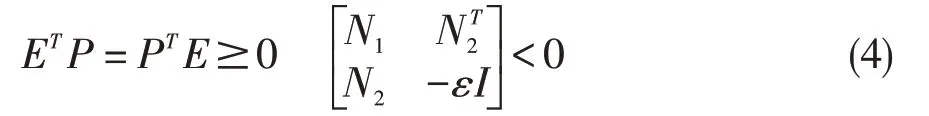
其中

则闭环系统(3)是严格无源的。

证明首先构造Lyapunov函数为

则V(x(t),e(t))是正定的，函数V(x(t),e(t))对时间求导得

其中

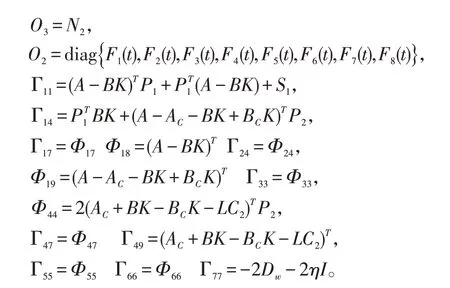
由引理1 与引理2 可得，上式对所有允许的不确定性成立，当且仅当Ω<0，使得

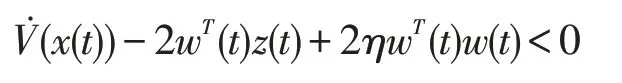
成立，由定义1知系统(3)是严格无源的。证毕。

定理2若存在可逆矩阵P1,P2,S1,S2,R1,R2, 矩阵K,L使得满足

则闭环系统（3）是时滞依赖无源的，并得到控制器增益与观测器增益分别为

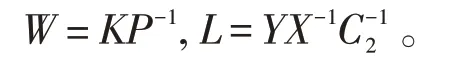
3 结语

主要针对不确定时滞广义系统，通过构造Lyapunov函数,由线性矩阵不等式的方法, 再利用引理得出系统时滞依赖无源的充分条件，同时给出了观测器的设计，也得出了控制器增益矩阵和观测器增益矩阵。