自旋翻转系数对量子点系统热电的影响

许 丽,高彩云

（山西大同大学物理与电子科学学院，山西大同 030009）

量子输运理论中的电荷特性和自旋特性已引起科研工作人员的关注[1-2]。巨磁阻效应于2007年被格姆伯格和佛特发现，标志着自旋可以作为能流和信息的载体。随着自旋动力学的发展，在实验上通过自旋的旋进、自旋的分离等方法实现了对固体态内自旋的调控。Leo Kouwenhoven 小组于2004年通过电荷传感实验可以准确地测量出电子在器件中运动的时间。近年来科研工作者已经实现了对自旋的控制，为进一步实现自旋器件打下了良好的基础[3-4]。由于铁磁电极的磁性特性导致费米面附近自旋向上的载流子与自旋向下的载流子数不相等，在量子输运中出现自旋极化输运，进而在杂化结构中展现出一些新的现象，例如：Fano effect[5],kondo effect[6]。通过调节磁场、翻转系数和磁矩各参数，铁磁电极可以用作自旋的注入和分离，来实现对电子自旋特性的研究。文章通过采用非平衡格林函数方法来研究量子输运问题，我们考虑一个量子点、铁磁电极和金属电极组成的系统，通过调节量子点内的自旋翻转、无量纲常数α和磁化夹角来研究该系统的热电特性。

1 电流公式的推导

我们选择的模型由一个能级简并的量子点、铁磁电极和正常金属电极组成的量子点系统，如图1所示。

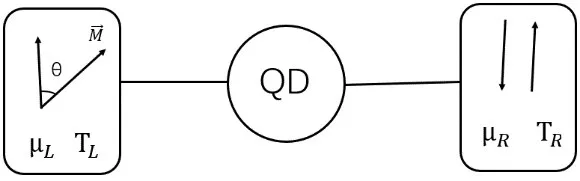
图1 量子点QD通过导线与左右电极相连的模型示意图

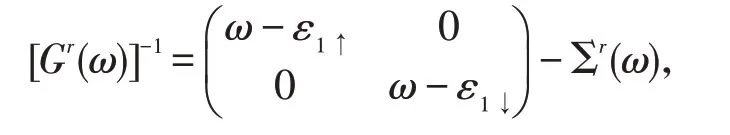
矩阵Σr(ω)是推迟格林函数，它是由点内自旋翻转引起的推迟自能(ω)、点与电极α(α=L,R)间隧穿引起的推迟自能(ω)组成的，即：Σr(ω)=

近似认为能带较宽的条件下[10-11]，是常数。

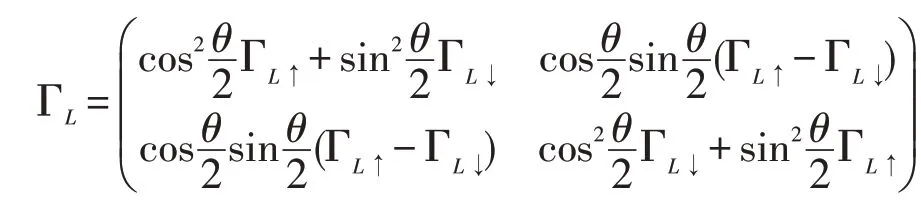
当左右电极的偏压和温度梯度趋近于零时，该系统的热电系数(电导、热电势、热导、热品质因子)的表达式为[12-14]：

2 数值模拟分析

在左右电极化学势为零的条件下，我们通过数值模拟来分析由于温差效应引起量子器件的热电问题。由于量子点内翻转系数的存在，量子点的简并能级被劈裂成有效的双能级ε±=ε±η，与热电输运中spin-minority 电子通道和spin-majority 电子通道相对应。铁磁电极的磁化夹角在电极内也会引起自旋翻转，使系统的热电效应也发生改变。通过调节量子点内翻转系数和铁磁电极的磁化，使量子系统内的热电输运达到最佳的条件。

图2 显示了在系统参数为p=0.5,θ=0.3π ,kBT=0.1Γ, Γ=1meV,α=1 的条件下，系统热电系数（a 电导 G，b 热电势S，c 热电品质因子ZT）随着量子点内翻转系数变化的热电特性。随着点内自旋翻转系数的增加，电导光谱（如图a）的双峰对称的向两边移动, 峰的幅值保持不变。在参数的选取中极化强度和磁化夹角保持不变，电子通道的宽度不变导致电导谱的峰值不变。电导峰的位置对应于自旋翻转系数±η，所以随着的增加，谱峰向两边对称的分开。在spin-majority电子通道中热电势（如图b）几乎不变，而在spin-minority 电子通道中热电势（如图b）增加的幅度较大。热品质因子ZT光谱的变化趋势与热电势相似，但是在±η位置ZT的双峰靠近费能级峰增加的较快，体现了在费米面附近，温度对电子输运的影响较大些。

在实验过程中，很难实现量子点与电极间完全对称地耦合。因而我们在理论模拟中会引入一个左右电极与量子点耦合强度间的一个无量纲比值α=ΓF/ΓN，来分析耦合强度不对称性引起的spinminority 电子通道和spin-majority 电子通道中的热电输运问题。图3 显示了在系统参数为Γ=1meV,η=1Γ,θ=0.3π ,kBT=0.1Γ,p=0.3 的条件下，系统热电系数（a 电导 G，b 热电势S，c 热电品质因子ZT随着无量纲比值α和ε=Eu↑变化的热电特性。随着无量纲比值α的增加，电导光谱（如图a）的双峰位置不变,峰的幅值逐渐的减小。当α增加时，左电极与量子点的耦合强度大于右电极与量子点的耦合强度。相对而言，从左电极输运的电子隧穿率增加，导致电导谱随着α的增加而逐渐的增加。由于自旋翻转系数η不变，导致电导谱峰的位置不变。如图b热电势和图c的热因子ZT随之无量纲比值α的增加而逐渐的降低。

图3 系统热电系数随着无量纲比值α 变化的热电特性

图4(a)显示了在系统参数为Γ=1meV,η=1Γ,θ=0.3π ,kBT=0.1Γ,p=0.3 的条件下，热品质因子ZT 随着ε和α变化的三维图可以看出来，在无量纲常数α极小值范围内展现出最佳的热电效应。随着无量纲常数α的增加，ZT 的值逐渐的减小。

图4(b)显示了在系统参数为Γ=1meV、η=2Γ、p=0.5、kBT=0.1Γ、α=0.05 的条件下，随着铁磁电极的磁化夹角θ逐渐增加，系统电导G光谱随着位能级ε的变化特性。电导谱在±η处波峰保持不变，与磁化夹角无关。在spin-majority 电子通道中的电导光谱逐渐增加，而spin-minority 电子通道中电子光谱逐渐的减小。因为spin-majority电子通道的振幅正弦函数决定，而spin-minority 电子通道的振幅由余弦函数决定。

图4 系统电导G 光谱随着位能级ε 的变化特性

3 结论

我们基于共隧穿来分析点内自旋翻转和电极内翻转对热电的影响。在两电极的化学势均为零的条件下，通过调节量子点内翻转系数和铁磁电极的磁化，来研究由于温差效应引起量子器件的热电问题，进而寻找系统内热电输运的最佳条件。由于量子点内翻转系数的存在，量子点的简并能级被劈裂成有效的双能级ε±=ε±η，相对应于热电输运中spin-minority电子通道和spin-majority电子通道。电导光谱的位置只决定于自旋翻转系数±η，所以随着自旋翻转系数的增加，两个峰的位置逐渐地向两边移动。电子通道的宽度随着电极的极化强度、无量纲比值和铁磁电极磁化的改变而改变，所以电导谱的幅值取决于极化强度、无量纲比值和铁磁电极磁化。随着的无量纲比值α增加，电导谱峰逐渐降低。因为spin-majority电子通道中振幅由正弦函数决定，而spin-minority电子通道中振幅由余弦函数决定。所以随着铁磁电极的磁化夹角θ逐渐增加，在spin-majority电子通道中的电导光谱逐渐增加，而spin-minority电子通道中电导光谱逐渐的减小。在±η位置处，ZT靠近费能级的双峰增加的较快，体现了在费米面附近温度对电子输运的影响较大些。在无量纲常数α极小值范围内可以等到最佳的热电效应。