无刷电机调速系统的仿真研究

董 莹

（青海民族大学物理与电子信息工程学院，青海西宁810007）

无刷直流电机被广泛运用于工业自动化、汽车工业、航天航空等各个领域，具有很强的现实应用价值。调速系统是电机的关键，随着时代与工业化的发展对无刷直流电机的调速系统性能的要求也越来越高，设计具有高性能的电机调速系统对于实际生产非常重要[1]。许多有序的学者致力于无刷直流电机调速系统的研究，石征锦（2016）等人在基于Matlab/Simulink 仿真平台搭建了BLDCM 调速系统仿真模型并进行了仿真实验；邓元望(2018)等人就基于无刷直流电机模型的基础上提出了一种优化的控制算法，并建立了Matlab/ Simulink 仿真模型进行了仿真测试结果显示大幅度提高了系统的稳定性，由此可见无刷电流机系统模型的构建之间影响到电机的性能，是无刷直流电机发展的重点研究内容。对此文章主要建立无刷电流机的双闭环调速系统模型，并利用Simulink模块对无刷直流电机调速系统进行仿真研究，是否达到预期要求，从而指导实际生产。

1 无刷电机双闭环调速系统

1.1 系统的工作原理

调速系统主要是对转速进行控制。与单闭环相比，电流环和转速环双闭环调速系统可以弥补电枢回路电阻的压降。双闭环调速系统电路原理如图1 所示，图中的ASR 代表的是转速调节器，用来调节电动机的转速，而ACR 则代表着电流调节器，用来调节电枢电流。两个调节器串联，转速调节器的输出经过限幅后给到电流调节器的输入，限幅的作用是保护调节器，防止电压电流过高损毁设备，而电流调节器的输出经过限幅后给到电力电子变换器的输入。电流环在内部，被称为内环；转速环在外部，被称为外环。转速调机器和电流调节器的输出都带有限幅，电流调节器ACR的给定电压最大值Uim取决于转速调节器ASR 的输出限幅什Uim，以此类推。

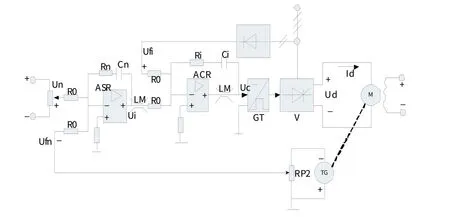
图1 双闭环调速系统电路原理图

1.2 数学模型的建立

本次数学模型的构建参照两极三相无刷直流电机，电动机定子绕组接法采用Y 型接法，绕组形式采用集中整距绕组形式。电动机转子结构是隐极内转子结构。在电动机空间上相隔120度分别放置一个霍尔元件，总共放置三个霍尔元件。根据以上条件，作出以下假设：

(1)假设电机的铁心是不饱和的，同时不计涡流与磁滞损耗;

(2)假设电机不发生电枢反应;

(3)假设不存在齿槽效应，电枢导体均匀分布;

(4)驱动电路的续流二极管和功率元件都具备理想的开关特性。

根据假设条件可得：

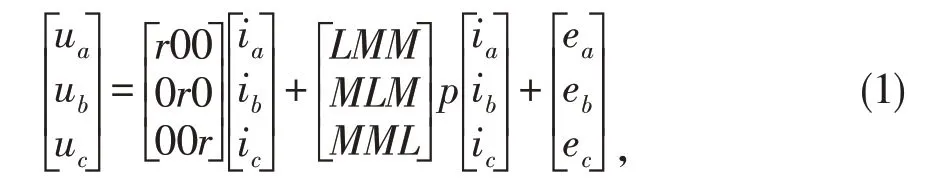
其中，P为微分算子，L为每相绕组的自感，M为每两相绕组的互感。定子绕组的互感，自感均是常数。Ea、eb、ec分别为三相定子反电动势。因三相绕组连接方式为Y型，电动机三相绕组没有中线时，则有[2]：

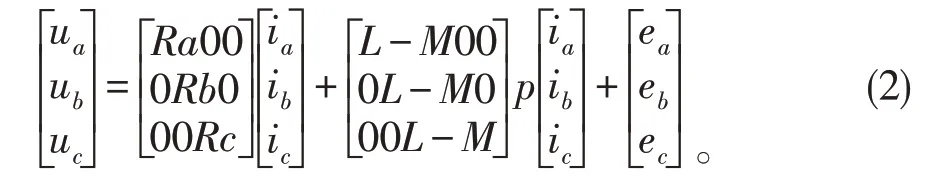
电磁转矩为：Td=(eaia+ebib+ecic)。在直流无刷电动机通电期间，它的带电导体处在相同的磁场下，每一相绕组的电动势都是：

其中，Pm为电动机极对数，N为总导体数，n为电动机转速。则有

所以有：

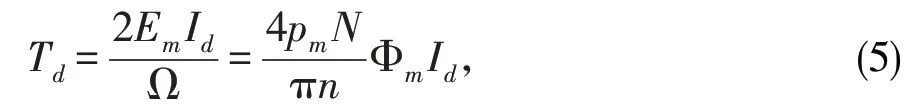
其中，Id为方波电流的幅值，Ω为电机的角速度(rad/s)，Ω 为2πn/60。

由式（5）可以得到以下结论：通过控制逆变器输出波电流幅值就可以控制直流无刷方波电机的电磁转矩。而且电动机转子的运动方程为：

通过进一步化简可得

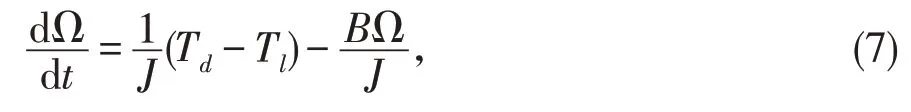
其中：Tl为负载转矩，J为转子与负载的转动惯量，B为粘滞阻尼系数。

本系统中的三相逆变器在任何时刻只有两相导电，而且电机的输出相电压幅值为因此，每相绕组的动态方程式为式（8），其中Us为电源电压

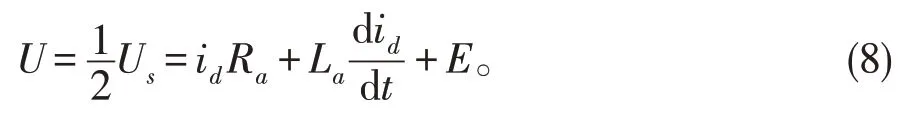
考虑到理想状态下，因此忽略粘性摩擦，那么电动机的转矩平衡方程式为：

由式(8)可得：

在对式(8)和式(10)两边分别进行拉式变换后可得：

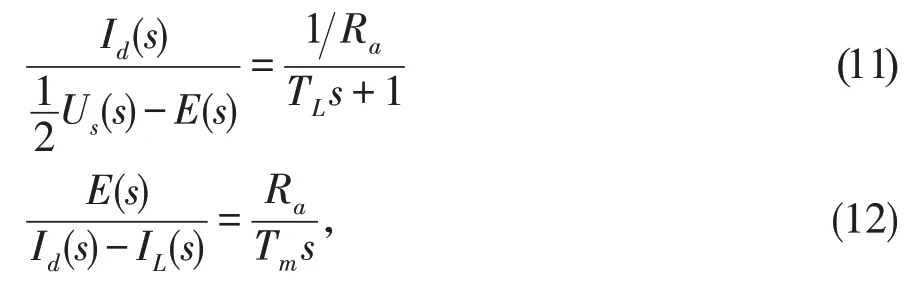
联合式(11)和式(12)，同时考虑到E=Cen，在此可得到直流无刷电机的动态结构图，如图2 所示。其传递函数为：

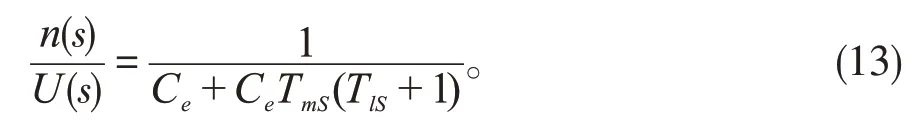
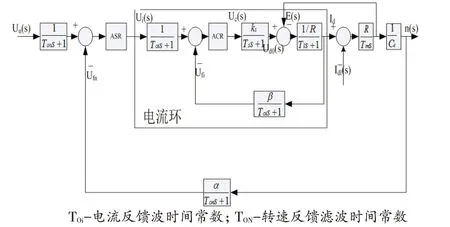
图2 双闭环调速系统的动态结构框图

图2为双闭环调速系统的动态结构框图，该图是由双闭环调速系统与直流无刷电机整合而来，但是因为电流检测信号中存在交流分量，必须施加低通滤波，它的滤波时间常数Toi按需要来整定。因为转速换和电流环相似，所以要在转速给定通道中也配上给定滤波环节，时间常数为Ton。这两个常数根据实际来整定[3]。

2 双闭环直流调速系统调节器设计

2.1 电流调节器的设计

1）确定ASR的时间常数

（1）电路中为了整流需要设置整流装置，整流装置需要确定滞后时间常数，这个常数我们在这设为Ts。那么三相全控桥电路的Ts为0.0017 s。

（2）电路中为了滤波我们需要添加一个滤波装置，该滤波装置的滤波时间常数我们通常设为Toi。在日常的生产中，一个三相全控桥电路种每个波头的时间大约是3.3 ms，波头对实验会产生干扰，所以我们需要滤平波头，在这近似取1 到2 倍的Toi=3.3 ms，那么可得Toi=2 ms=0.002 s。

（3）滞后时间常数加上滤波时间常数即为TΣi。取得TΣi=Ts+Toi=0.0037 s。

2）选择电流调节器的结构

本次设计中，对于静差率的要求是低于5%，即σi≤5%，还要求电流到达稳态时能够与经过比例调节能够恢复到预定值，典型Ⅰ型系统恰恰可以满足这两个条件，所以就按照这个进行电流调节器设计。PI型调节器适用于多种情况，其中包括控制对象是双惯性的，在此，电流环控制的对象恰恰如此，所以可对电流环进行PI设计。传递函数为

对电源电压的抗干扰性能进行检查：Tl/TΣi=0.033/0.0037=8.92,可知典型I型系统的动态抗扰性能，各项指标都在可接受范围之内，所以上述满足条件。

3）电流调节器的参数计算

ACR超前时间常数：τi=Tl=0.033 s。

电流开环增益：要求σi≤5%时，取KITΣi=0.5，因此，

ACR 的比例系数Ki=（KIτiR）/（K是β）=（135.1*0.033*3.7）/(27*0.77)=0.793

故而，我们取R0=40K，则Ri= KiR0=0.793*40=31.72K，Ci=τi/Ri=0.033/31720=1uf，Coi=4Toi/R0=4*0.002/4k=0.2uf。

2.2 转速调节器的设计

1）确定ASR的时间常数

（1）在此我们设电流环ASR 等效时间常数为1/KI。根据上述可知，KITΣi=0.5，得

（2）转速环中需要设置滤波装置，我们设滤波时间常数为Ton，取Ton=0.01 s。

（3）转速环等效时间常数加上滤波时间常数等于TΣn。得

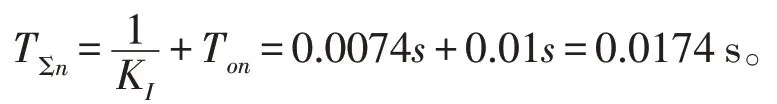
2）选择转速调节器结构

根据设计要求，采用PI调节器，传递环数为

3）计算ASR参数

转速负反馈作为电机转速到达稳态后其主要作用的调节器，不仅需要转速调节器跟随性能好还需要较强的抗干扰的能力，综合考虑取h=5，则ASR的超前时间常数为

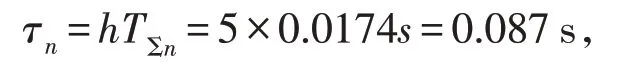
则转速环开环增益

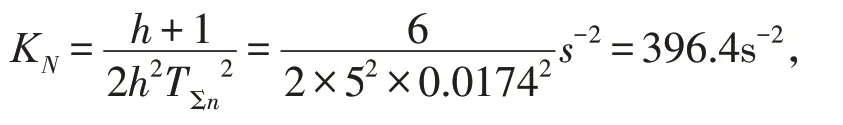
可得ASR的比例系数为

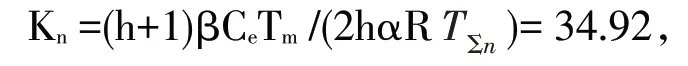
式中：电动势常数Ce=(Un-InRn)/Nn=(220-6.5*3.7)/1500=0.131。

转速反馈系数α=0.007Vmin/r。

取R0为40K，则

RN=KNRO=34.92*40K=1396.8KΩ，

Cn=τi/Rn=0.087/1396.8k=0.06uf，

Con=4Ton/R0=4*0.01/40K=1uf。

3 仿真设计

3.1 模型建立

根据前面构建的系统数据模型，建立仿真模型如下图3 所示。本次实验仿真MATLAB 中的Simulink模块对建立的模型进行仿真效果检验。

3.2 参数设置

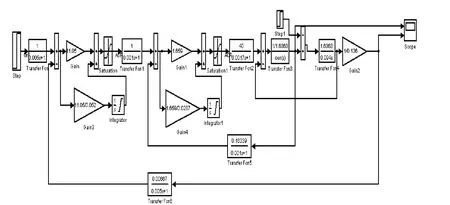
图3 系统动态结构仿真模型图

在建立仿真模型的过程中，对Simulink 模块进行参数设置比较困难，但也是整个仿真的关键。在仿真过程中我们需要对参数进行不断的调整，来获得比较好的仿真效果，从而为现实系统的实现提供设计依据[4]。通过不断的仿真实验，发现Saturation饱和模块1和Integrator 模块1的参数对于两个输出波形影响较小，所以在Saturation饱和模块1中设置的“Upper limit”和“lower limit”分别为10、-2，Integrator 模块 1 的参数“Upper Saturation limit”和“lower Saturation limit”分别为 8、-2。对 Saturation 模块和Integrator 模块两个模块中的“Upper limit”、“lower limit”、“Upper Saturation limit”和“lower Saturation limit”的参数设置分别为5、-2、3、0。

3.3 结果讨论

根据模块设置的参数所得到的调速系统的电流和转速仿真结果如图4 图5 所示。因电动机的额定电压为220 V，赋予仿真以220 V 的阶跃信号应得到1460 r/ min 左右的转速，从仿真结果上显示，构建的无刷电机调速系统模型满足要求。

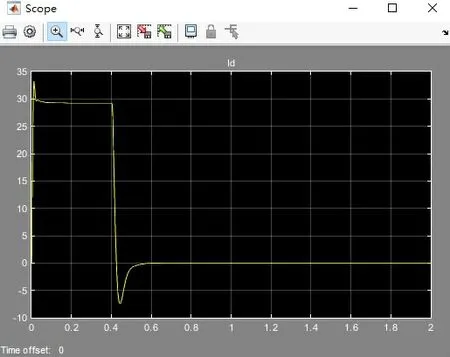
图4 Saturation“上限”为5的电流仿真结果

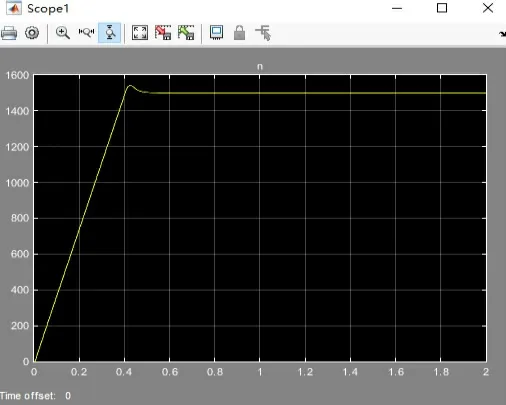
图5 Saturation“上限”为5的转速仿真结果

对Saturation模块参数中的上限“Upper limit”从5调整至10，保持Integrator模块参数设置不变，得到的仿真结果如图6、图7所示。

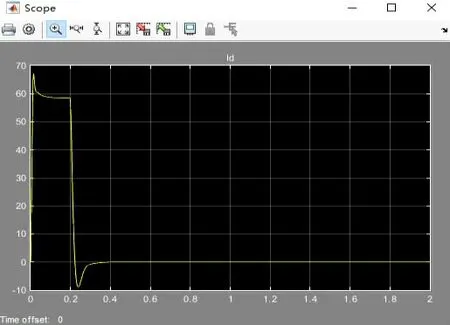
图6 Saturation“上限”为10的电流仿真结果

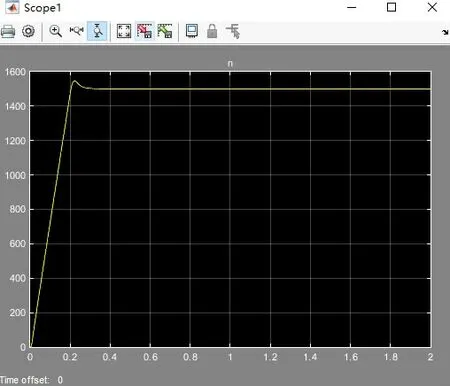
图7 Saturation“上限”为10的转速仿真结果

在上面的参数结果上，当保持Integrator模块参数设置不变，将Saturation模块参数中的上限Upper limit”从10继续上调调整至15时，仿真结果如图8和图9所示。

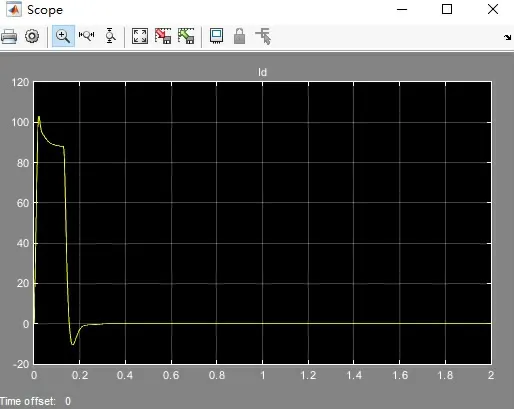
图8 Saturation“上限”为15的电流仿真结果

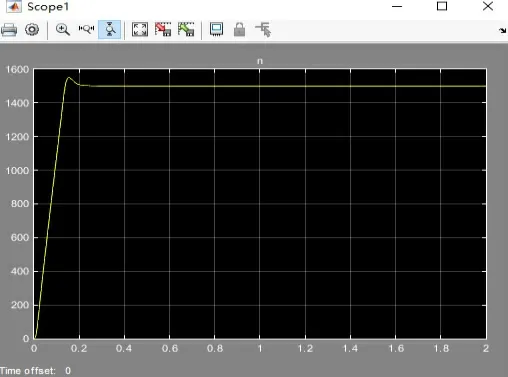
图9 Saturation“上限”为15的转速仿真结果

根据以上的仿真结果图对比不难发现，Saturation 模块设置中的Upper limit 数值决定了电流仿真的数值，当参数越大，电流所达到的最大值越大，在此设置Upper limit为10，电流波形较为正常。通过参数调整，当Saturation模块中的Upper limit数值为 10，Integrator 模块 Upper Saturation limit 为 3 时，仿真效果达到最佳。本次仿真结果显示所构建的无刷电机双闭环调速系统模型具有良好的仿真效果，性能较好，具有很强的系统实用价值。

4 结论

与单闭环调速系统相比，双闭环调速可以依靠电流和转速环两个量的负反馈对转速进行调节，分别利用电流调节器和转速调节器，分工合作，实现自己的功能，具有较强的优势特点。对此，建立采用双闭环调速系统，构建相应的数学模型，并利用simulink 仿真平台进行仿真，仿真结果显示所构建的无刷电机双闭环调速系统模型具有良好的仿真效果，并在Saturation 模块中的Upper limit 数值为10，Integrator 模块 Upper Saturation limit 参数为 3 时达到最佳，达到预期效果。