山西采矿区地质灾害下局部电网的灾变脆弱性评估*
韩俊玉,魏丽峰,梁 灏
(国网山西省电力公司检修分公司,山西 太原 030032)
计算机网络技术的快速发展,电网技术也随之迅速崛起,电网的快速建设、远距离、高压、大容量输电线路的出现形成大规模的电力系统[1]。现阶段地质灾害下局部电网的灾变脆弱性评估中,普遍存在着评估所需时间过长[2-3],准确度较低,脆弱性评估值与实际评估值不符等问题。针对上述问题,能够有效的提出一种具有较高检测效率的方法成为当今社会亟待解决的问题[4-5]。
丁少倩等[6]提出一种基于短路容量的新能源电网脆弱性评估方法。该方法通过对新能源电网进行分析,在新能源电网脆弱性的基础上,利用PAM分类的方法和评价指标来对检测出的电网脆弱节点进行自动分类,以此完成新能源电网脆弱性评估。该方法具有较高的可行性和适用性,但是在进行脆弱性评估的过程中评估所需时间过长。王涛等[7]提出一种基于模糊决策法的电网脆弱性评估方法。该方法利用最小奇异值测量电网电压节点之间的距离,体现各个节点之间电压稳定状态,利用潮流熵网络架构完整程度体现电网系统平均负载率,采用模糊决策法综合评价电网脆弱性节点,完成电网脆弱性评估。该方法在评估所需时间较短,但是在评估过程中利用网络架构完整程度体现电网系统平均负载率容易存在误差,脆弱性准确度较低。
针对上述问题,本文提出一种基于理想解排序法的局部电网灾变脆弱性评估方法。实验结果表明,本文所提出方法脆弱性评估所需时间较短、准确度较高。
1 山西采矿区地质灾害下局部电网的灾变脆弱性评估
1.1 获取局部电网灾变脆弱性量化结果
利用贝叶斯攻击图对山西采矿区地质灾害下局部电网进行建模,结合地质灾害攻击意图和原子攻击的特性,采用不同概率特征对局部电网各属性节点进行更新,通过更新结果得到局部电网灾变脆弱性量化结果。贝叶斯攻击图可以分为局部电网的状态攻击图和电网属性攻击图两部分,电网属性攻击图能够从地质灾害攻击角度展示出电网受到攻击的情况,为了有效的避免地质灾害下局部电网受到攻击时发生的爆炸问题,采用贝叶斯理论与地质灾害下局部电网的属性攻击图相结合,构建贝叶斯攻击图对山西采矿区地质灾害下局部电网进行建模。

P(Ei)=PAV×PAC×PAU。
(1)
式中:PAV、PAC、PAU分别表示攻击途径、身份认证以及攻击难易程度的评分值。
在对地质灾害下局部电网进行攻击时,不同的攻击策略得到的攻击收益具有差异性。在攻击方完全理性的情况下,会选取收益最大的攻击方式对电网进行攻击。攻击方的攻击意识∂(Ei)可根据选取的攻击策略Ei面临的攻击压力Apress以及可取得的最大收益来体现。
攻击最大收益是指攻击方采取某种攻击方式进行单次原子攻击时所面临的风险,主要包含实施攻击策略所付出的代价与成本这两个方面。其中,实施攻击策略需要付出的代价与原子攻击自身的价值以及执行这次攻击对自身的损失有关;实施攻击策略的成本与实施攻击过程中的执行代价和攻击实施成功所需时间相关。以上影响原子攻击的攻击代价以及成本的所有因素均视为攻击目标网络的压力影响因子,其量化形式可根据漏洞评分系统中对脆弱点的量化标准执行。根据攻击压力影响因子所处等级以及相应的权值进行汇总,最终获得原子攻击攻击目标网络的压力量化值。
攻击收益Apress(Ei)是实施单次攻击策略Ei所取得的收益,仅与实施完此次攻击策略后的攻击状态相关,在实施后续攻击策略后并不能获得与单次攻击相同的攻击收益。根据地质灾害下局部电网的实际运行情况,对实施完攻击策略后的攻击状态划分等级,结合专家给出的意见对不同攻击状态等级赋予不同的权重,该值即为攻击方采取某种攻击策略后所得到的最终状态所相应的收益。
攻击方的攻击意识可根据原子攻击目标网络时的压力以及攻击成功情况下所获收益的比值来体现,比值越大,说明该攻击策略被实施的概率越小;相反,则说明该攻击策略被实施的概率越大。综上所述,攻击方采取某种攻击意识的压力与收益之间的比值利用下式表示:
(2)
以公式(2)为基础,利用下式给出攻击方以某种攻击方式进行攻击的攻击意识:
(3)
当满足∂(Ei)=0时,攻击方采取某种攻击策略对目标网络进行攻击时的压力大小不小于攻击成功所取得的攻击收益,攻击方不会选取这种攻击方式;当满足∂(Ei)=1时,攻击方攻击目标网络的压力为0,说明攻击方实施某种攻击策略时不会有任何攻击损失,则攻击方应优先选取此攻击策略;当满足0<∂(Ei)<1时,攻击方会选取攻击意识较强的攻击策略。
局部条件概率主要体现在某个单独的局部电网灾害属性状态节点受到地质灾害攻击威胁的可能性,与父节点到该受到灾害节点的原子攻击有关,地质灾害采用攻击策略Ei从父节点向子节点进行地质灾害攻击时,局部电网灾害属性状态成功转移的概率Pstatus(Ei)与地质灾害攻击者的攻击意图和地质灾害下局部电网原子攻击成功的概率有关,即:
Pstatus(Ei)=P(Ei)×∂(Ei)。
(4)
当Par(Sj)代表山西采矿区地质灾害属性节点Sj的父节点集合,利用父子节点之间互相依赖的关系,则局部条件概率可分为两种情况:
第一种情况,在地质灾害攻击下局部电网父子节点的依赖关系为AND时,即:

(5)
第二种情况,在地质灾害攻击下局部电网父子节点的依赖关系为OR时,即:

(6)
为了能够更准确地评估地质灾害下局部电网的灾变脆弱性状况,需要求出贝叶斯攻击图中各个局部电网属性状态节点的可达概率,根据在地质灾害攻击下局部电网父子节点的情况获取出各个子节点的先验概率,利用下式给出,其表达式为:
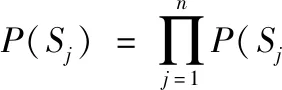
(7)


(8)
利用式(9)和式(10)对式(8)进行更新,可得:

(9)
(10)
通过更新结果得到局部电网灾变脆弱性量化结果:
ε=1-P(ε≤ε0) 。
(11)
1.2 基于理想解排序法的局部电网灾变脆弱性评估方法
根据局部电网灾变脆弱性量化结果,构建局部电网灾变指标层判断矩阵,根据该判断矩阵的最大特征值和特征向量获取各个节点之间的组合权重,对评价指标值进行规范化处理,得到地质灾害下局部电网的灾变脆弱度因子,构建局部电网灾变脆弱性评估模型,完成评估。
根据山西采矿区地质灾害下局部电网的灾变脆弱性量化结果,构建局部电网灾变指标层判断矩阵,利用AHP中经常见的互反性从1~9的标度法,对不同地质灾害因素进行两两比较,得到该判断矩阵为A=(aij)n×n,式中,aij代表地质灾害指标i相对于指标j的重要程度。
根据局部电网灾变指标层判断矩阵A计算出该矩阵的最大特征值和特征向量,得出各个节点之间的组合权重为:
(12)
式中:WP代表局部电网灾变指标层上n上节点相对于λ的组合权重向量,(W1jp,W2jp,…,Wnjp)代表局部电网灾变指标层的权重矩阵。
在山西采矿区地质灾害下局部电网中有m个行为的n个指标层因素构造的决策矩阵B=(bij)m×n,利用下式形成地质灾害局部电网规范化决策矩阵为:
(13)
(14)
以公式(14)为基础,获取地质灾害下局部电网灾变脆弱度因子:
(15)
利用公式(15)中获取的脆弱度因子构建地质灾害下局部电网的灾变脆弱性评估模型:
(16)
2 实验与仿真证明
为了验证本文所提出基于理想解排序法的局部电网灾变脆弱性评估方法的综合有效性,将本文所提出方法与基于短路容量的新能源电网脆弱性评估方法和基于模糊决策法的电网脆弱性评估方法进行对比实验,实验结果如下所示。
将本文所得出的方法与基于短路容量的新能源电网脆弱性评估方法和基于模糊决策法的电网脆弱性评估方法进行脆弱性评估所需时间对比实验,实验结果如表1所示,表1中,方法1代表本文所得出的方法、方法2代表基于短路容量的新能源电网脆弱性评估方法、方法3代表基于模糊决策法的电网脆弱性评估方法。分析表1可知,3种方法都随着样本数量的不断增加,评估所需时间也随之发生着变化,本文得出的方法在样本数量不断增加的同时,评估所需时间也随之增加,当样本数量从20个增加到80个时,评估所需时间相差12 s。基于短路容量的新能源电网脆弱性评估方法当样本数量从20个增加到80个时,评估所需时间相差23 s,基于模糊决策法的电网脆弱性评估方法当样本数量从20个增加到80个时,评估所需时间相差54 s,实验结果表明,本文所得出方法评估所需时间最短,具有较高的应用性能。
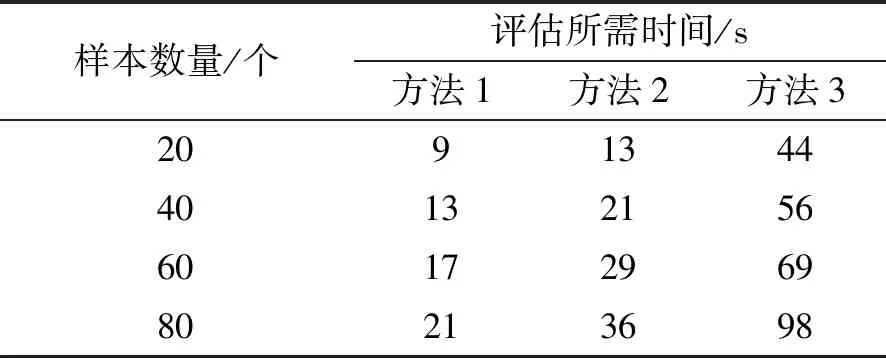
表1 不同方法评估所需时间对比实验
评估准确度对比实验,实验结果如表2所示,表2中,方法1代表本文所得出方法、方法2代表基于短路容量的新能源电网脆弱性评估方法、方法3代表基于模糊决策法的电网脆弱性评估方法。分析表2可知,3种方法都随着样本数量的不断增加,评估准确度都有所降低,当样本数量为11个时,基于短路容量的新能源电网脆弱性评估方法和基于模糊决策法的电网脆弱性评估方法评估准确度与本文所得出方法评估准确度之间分别相差1.88%和4.55%。当样本数量为41个时,基于短路容量的新能源电网脆弱性评估方法和基于模糊决策法的电网脆弱性评估方法的评估准确度与本文所提出方法评估准确度之间分别相差2.13%和6.8%。实验结果表明,本文所给出方法评估准确度相对最高,基于模糊决策法的电网脆弱性评估方法评估准确度最低。

表2 不同方法评估准确度对比实验
电网脆弱性评估与实际评估值对比实验,实验结果如图1所示,图1中,W代表实际评估值,Y代表本文所得出方法评估值,Q代表基于短路容量的新能源电网脆弱性评估方法评估值,H代表基于模糊决策法的电网脆弱性评估方法评估值。分析图1可知,3种方法电网脆弱性评估值都随着样本数据数量的不断增加,也随之发生一定的改变,基于短路容量的新能源电网脆弱性评估方法评估值的电网脆弱性评估值一直在30%以上,距离实际评估值较远,基于模糊决策法的电网脆弱性评估方法评估值一直处于较低的状态,距离实际评估值也相对较远、而本文所提出方法电网脆弱性评估值与实际值之间基本相符,具有相对较高的评估价值。
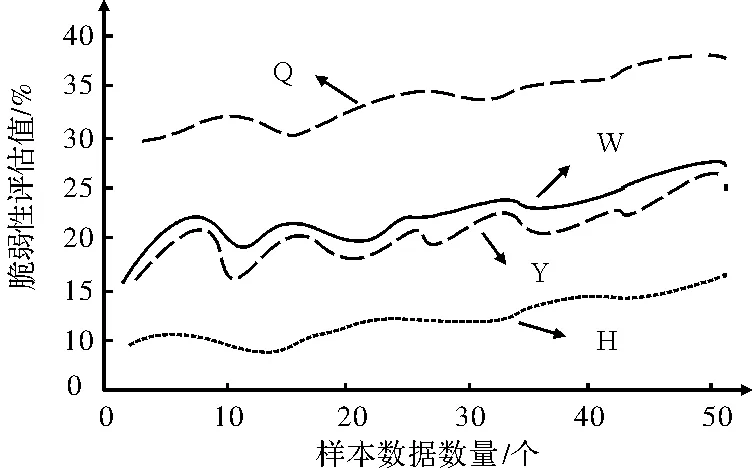
图1 不同方法电网脆弱性评估对比图
3 结束语
(1)山西采矿区地质灾害频发[8-10],电网的大范围覆盖,导致在地质灾害下的灾变损失较大,需要对局部电网的灾变脆弱性进行评估。本文提出了一种基于理想解排序法的局部电网灾变脆弱性评估方法。
(2)利用贝叶斯攻击图对山西采矿区地质灾害下局部电网进行建模,采用不同概率特征对局部电网各属性节点进行更新,通过更新结果得到局部电网灾变脆弱性量化结果。
(3)构建局部电网灾变指标层判断矩阵,根据该判断矩阵的最大特征值和特征向量获取各个节点之间的组合权重,对评价指标值进行规范化处理,得到地质灾害下局部电网的灾变脆弱度因子,构建局部电网灾变脆弱性评估模型,完成评估。
(4)该方法在评估过程中利用网络架构完整程度体现电网系统平均负载率容易存在误差,脆弱性准确度较低。

