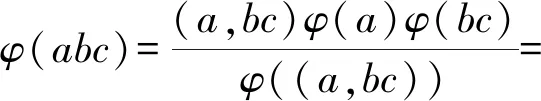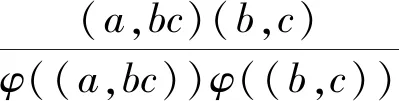三元欧拉函数方程φ(abc)=φ(a)+3(b)+5φ(c)的正整数解

梁晓艳，高 丽，高 倩

(延安大学数学与计算机科学学院，陕西延安716000)

对于任意正整数n，欧拉函数φ(n)表示1，2，…n-1中与n互素的正整数的个数。欧拉函数在数论中有着重要的作用，近年来，有关欧拉函数的性质以及欧拉方程吸引了很多学者的兴趣。在文献[1-7]中分别研究了k=2，4，5，6，7，8，9时欧拉函数方程φ(ab)=k(φ(a)+φ(b))的全部正整数解。文献[8-10]研究了三元欧拉函数方程当k=3，4，5时φ(abc)=k(φ(a)+φ(b)+φ(c)的全部正整数解。文献[11]研究了四元欧拉方程φ(abcd)=2(φ(a)+φ(b)+φ(c)+φ(d)的全部正整数解。文献[12]研究了三元变系数欧拉方程φ(abc)=2φ(a)+3φ(b)+4φ(c)的全部正整数解。本文在前人研究的基础上，利用初等数论的相关知识研究了欧拉函数方程φ(abc)=φ(a)+3(b)+5φ(c)的正整数解。

1 相关引理

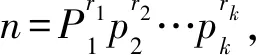
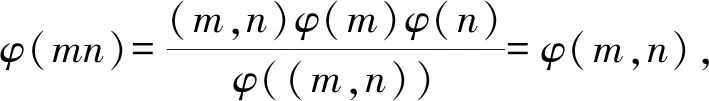
当(m,n)=1时，有φ(mn)=φ(m)φ(n)。

引理3[1]当n≥2时，有φ(n)

引理4[1]在欧拉函数方程φ(abc)=k+hφ(c)中，若φ(ab)≥k+h+1，则该方程无正整数解。

2 结论及证明

定理1 欧拉函数方程φ(abc)=φ(a)+3(b)+5φ(c)共有19组正整数解，其解为：

(a，b，c)=(2，14，2)，(2，18，2)，(3，5，3)，(3，8，3)，(3，10，3)，(3，5，6)，(6，5，3)，(3，4，13)，(4，3，13)，(15，1，2)，(15，2，1)，(16，1，2)，(16，2，1)，(20，1，2)，(20，2，1)，(24，1，2)，(24，2，1)，(30，1，2)，(30，2，1)。

证明：对于欧拉函数方程

φ(abc)=φ(a)+3(b)+5φ(c)

(1)

由引理3所以φ(a)+3φ(b)+5φ(c)=

φ(abc)≥φ(a)φ(b)φ(c)，

φ(a)+3φ(b)=φ(abc)-5φ(c)≥

φ(a)φ(b)φ(c)-5φ(c)，

(φ(a)φ(b)-5)φ(c)≥φ(a)φ(b)-5，

即(φ(a)-3)(φ(b)-1)≤8。

根据φ(a)、φ(b)的不同取值分10种情况分别进行讨论：

情况1：当(φ(a)-3)(φ(b)-1)<0时，则有

φ(a)=1,2,φ(b)>1。

1.1当φ(a)=1,φ(b)>1时，有

1+3φ(b)+5φ(c)=φ(abc)≥φ(b)φ(c)，

即(φ(b)-5)(φ(c)-3)≤16。

(1)当φ(a)=1,φ(b)=2时，φ(c)为任意值时，此时(1)为φ(abc)=7+5φ(c)，经检验，(1)无解。

(2)当φ(a)=1,φ(b)=4时，此时φ(abc)=13+5φ(c)，经检验，(1)无解。

(3)当φ(a)=1,φ(b)=6时，此时φ(c)-3≤16，即φ(c)=1，2，4，6，8，10，12，14，16，18。

若φ(c)=1,φ(abc)=24，即abc=35,39,45,52,56,70,72,78,84,90，又a=c=1,2,b=7,9,14,18，将a,b,c的值因子分解，在a,b,c中寻找相关因子，得(a,b,c)=(2,14,2),(2,18,2)使(1)成立。

若φ(c)=2，4，6，8，10，12，14，16，18时，

φ(abc)=19+5φ(c)，由引理3知(1)无解。

(4)当φ(a)=1,φ(b)=8时，此时φ(c)-3≤5，即φ(c)=1，2，4，6，8。

若φ(c)=1时，φ(abc)=30，即abc=31,62，经检验，(1)无解。

若φ(c)=2，4，6，8时，φ(abc)=25+5φ(c)，由引理3知(1)无解。

(5)当φ(a)=1,φ(b)=10时，此时φ(c)-3≤3，即φ(c)=1，2，4，6。

若φ(c)=1时，φ(abc)=36，abc=37，57，63，74，76，108，114，126，经检验，(1)无解。

若φ(c)=2，4，6时，φ(abc)=31+5φ(c)，由引理3知(1)无解。

(6)当φ(a)=1,φ(b)=12时，此时φ(c)-3≤2，即φ(c)=1，2，4。

若φ(c)=1时，φ(abc)=42，abc=43，49，86，98，经检验，(1)无解。

若φ(c)=2，4时，φ(abc)=37+5φ(c)，由引理3知(1)无解。

(7)当φ(a)=1,φ(b)=14时，此时不存在b使得φ(b)=14成立。

(8)当φ(a)=1,φ(b)=16时，此时φ(c)-3≤1，即φ(c)=1，2，4。

若φ(c)=1时，φ(abc)=54，abc=81,162，经检验，(1)无解。

若φ(c)=2,4时，φ(abc)=49+5φ(c)，由引理3知(1)无解。

(9)当φ(a)=1,φ(b)=18时，此时φ(c)-3≤1，即φ(c)=1,2,4。

若φ(c)=1时，φ(abc)=60，abc=61，77，93，99，122，124，154，186，198，经检验，(1)无解。

若φ(c)=2，4时，φ(abc)=55+5φ(c)，由引理3知(1)无解。

(10)当φ(a)=1,φ(b)=20时，此时φ(c)-3≤1，即φ(c)=1,2,4。

若φ(c)=1时，φ(abc)=66，abc=67,134，经检验，(1)无解。

若φ(c)=2,4时，φ(abc)=61+5φ(c)，由引理3知(1)无解。

(11)当φ(a)=1,φ(b)=22时，此时φ(c)-3≤1，即φ(c)=1,2,4。

若φ(c)=1时，φ(abc)=72，

abc=73,91，95，111，117，135，146，148，152，182，190，216，222，228，234，252，270，

经检验，(1)无解。

若φ(c)=2,4时，φ(abc)=67+5φ(c)，由引理3知(1)无解。

(12)当φ(a)=1,φ(b)≥22时，此时φ(c)-3<0，即φ(c)=1,2。

若φ(c)=1时，φ(abc)=6+3φ(b)，经检验，此时不存在满足φ(abc)=6+3φ(b)且φ(b)≥22的a,b,c，所以(1)无解。同理当φ(c)=2时(1)无解。

1.2当φ(a)=2,φ(b)>1时，有

φ(abc)=2+3φ(b)+5φ(c)。

(1)当φ(a)=2,φ(b)=2时，

φ(abc)=8+5φ(c)≥4φ(c)，

不存在c使(1)式成立。

(2)φ(a)=2,φ(b)=4时，

φ(abc)=14+5φ(c)≥8φ(c)，

即φ(c)≤4，即φ(c)=1，2，4。

当φ(c)=1,4时不存在a,b,c使(1)成立。

当φ(c)=2时，经检验，(a,b,c)=(3,5,3),(3,8,3),(3,10,3),(3,5,6),(6,5,3)。

(3)φ(a)=2,φ(b)=6时，

φ(abc)=20+5φ(c)≥12φ(c)，

即φ(c)≤2，即φ(c)=1,2。

若φ(c)=1时，φ(abc)=25，由引理3知(1)无解。

若φ(c)=2时，φ(abc)=30，abc=31,62，经检验，(1)无解。

(4)φ(a)=2,φ(b)=8时，

φ(abc)=26+5φ(c)≥16φ(c)，

即φ(c)≤2，即φ(c)=1,2。

若φ(c)=1时，φ(abc)=31，由引理3知(1)无解。

若φ(c)=2时，φ(abc)=36，abc=37,57,63,74,76,108,114,126，经检验，(1)无解。

(5)φ(a)=2,φ(b)=10时，

φ(abc)=32+5φ(c)≥20φ(c)，

即φ(c)≤2，即φ(c)=1,2。

若φ(c)=1时，φ(abc)=37，由引理3知(1)无解。

若φ(c)=2时，φ(abc)=42，abc=43,49,86,98，经检验，(1)无解。

(6)φ(a)=2,φ(b)=12时，

φ(abc)=38+5φ(c)≥24φ(c)，

即φ(c)≤2，即φ(c)=1,2。

若φ(c)=1时，φ(abc)=43，由引理3知(1)无解。

若φ(c)=2时，

φ(abc)=48,abc=65，104，105，112，130，140，144，156，168，180，210，

经检验，(a,b,c)=(3,4,13),(4,3,13)。

(7)φ(a)=2,φ(b)≥14时，

φ(abc)=44+5φ(c)≥28φ(c)，

即φ(c)=1。

若φ(c)=1时，φ(abc)为奇数，由引理3知(1)无解。

情况2：当(φ(a)-3)(φ(b)-1)=0时，φ(b)=1，φ(a)为任意值时，此时(1)为

φ(abc)=φ(a)+3+5φ(c)≥φ(a)φ(c)，

即(φ(a)-5)(φ(c)-1)≤8。

(1)当φ(c)=1且φ(a)为任意值时，此时

φ(abc)=8+φ(a)，由引理4知，φ(bc)=1,2≤8+1+1，所以方程有正整数解，

当φ(a)=8时，a=15,16,20,24,30,

有(a,b,c)=(15,1,2),(15,2,1),(16,1,2),(16,2,1),(20,1,2),(20,2,1),(24,1,2),(24,2,1),(30,1,2),(30,2,1)。

(2)当φ(c)=2时，φ(a)-5≤8，

即φ(a)=1,2,4,6,8,10,12。

若φ(a)=1,φ(abc)=14，不存在a,b,c使得

φ(abc)=14，所以(1)无解。

若φ(a)=2,4,6,8,10,12时，

φ(abc)=13+φ(a)，由引理3知(1)无解。

(3)当φ(c)=4时，φ(a)-5≤2，即

φ(a)=1,2,4,6。

若φ(a)=1,φ(abc)=24，即abc=25,39,45,52,56,70,72,78,84,90，经检验，(1)无解。

若φ(a)=2,4,6时，φ(abc)=23+φ(a)，由引理3知(1)无解。

(4)当φ(c)=6时，φ(a)-5≤1，即

φ(a)=1,2,4,6。

若φ(a)=1,φ(abc)=36，即abc=37,57,63,74,76,108,114,126，经检验，(1)无解。

若φ(a)=2,4,6时，φ(abc)=33+φ(a)，由引理3知(1)无解。

(5)当φ(c)=8时，φ(a)-5≤1，即

φ(a)=1,2,4,6。

若φ(a)=1,φ(abc)=44，即abc=69,92,138，经检验，(1)无解。

若φ(a)=2,4,6时，φ(abc)=43+φ(a)，由引理3知(1)无解。

(6)当φ(c)≥10时，φ(a)-5≤0，即

φ(a)=1,2,4。

若φ(a)=1,φ(abc)=4+5φ(c)，经检验，(1)无解。

若φ(a)=2,4时，φ(abc)=φ(a)+3+5φ(c)为奇数，由引理3知(1)无解。

情况3：(φ(a)-3)(φ(b)-1)=1时，则有

φ(a)=4,φ(b)=2，则

φ(abc)=10+5φ(c),a=5,8,10,12,b=3,4,6，

经检验，(1)无解。

情况4：(φ(a)-3)(φ(b)-1)=2时，则有

φ(a)=5,φ(b)=2或φ(a)=4,φ(b)=3，由引理3知(1)无解。

情况5：(φ(a)-3)(φ(b)-1)=3时，则有

φ(a)=4,φ(b)=4或φ(a)=6,φ(b)=2。

当φ(a)=4,φ(b)=4时，则

φ(abc)=16+5φ(c)≥16φ(c)，φ(c)≤1，

当φ(c)=1时，φ(abc)=21，由引理3知(1)无解。

当φ(a)=6,φ(b)=2时，则

φ(abc)=12+5φ(c)≥12φ(c)，φ(c)≤1，

当φ(c)=1时φ(abc)=17，由引理3知(1)无解。

情况6：(φ(a)-3)(φ(b)-1)=4时，则有

φ(a)=5,φ(b)=3或φ(a)=4,φ(b)=5或φ(a)=7，φ(b)=2，由引理3知(1)无解。

情况7：(φ(a)-3)(φ(b)-1)=5时，则有

φ(a)=4,φ(b)=6或φ(a)=8,φ(b)=2。

当φ(a)=4，φ(b)=6时,则

φ(abc)=22+5φ(c)≥24φ(c)，φ(c)≤1，

当φ(c)=1时，φ(abc)=27，由引理3知(1)无解。

当φ(a)=8,φ(b)=2时，则

φ(abc)=14+5φ(c)≥16φ(c)，φ(c)≤1，

当φ(c)=1时φ(abc)=19，由引理3知(1)无解。

情况8：(φ(a)-3)(φ(b)-1)=6时，则有

φ(a)=4,φ(b)=7或φ(a)=5,φ(b)=4或φ(a)=6,φ(b)=3或φ(a)=9,φ(b)=2，由引理3知(1)无解。

情况9：(φ(a)-3)(φ(b)-1)=7时，则有

φ(a)=4,φ(b)=8或φ(a)=10,φ(b)=2。

当φ(a)=4,φ(b)=8时，则

φ(abc)=28+5φ(c)≥32φ(c)，φ(c)≤1，

当φ(c)=1时，φ(abc)=33，由引理3知(1)无解。

当φ(a)=10,φ(b)=2时，则

φ(abc)=16+5φ(c)≥20φ(c)，φ(c)≤1，

当φ(c)=1时φ(abc)=21，由引理3知(1)无解。

情况10：(φ(a)-3)(φ(b)-1)=8时，则有

φ(a)=4,φ(b)=9或φ(a)=5,φ(b)=5或φ(a)=7,φ(b)=3或φ(a)=11,φ(b)=2，由引理3知(1)无解。

综上所述，可知方程φ(abc)=φ(a)+3(b)+5φ(c)有19组正整数解，证毕。