基于MCA的压缩感知彩色图像超分辨率重建

叶坤涛， 刘继锋， 郭振龙， 贺文熙

（江西理工大学理学院，医学信息工程研究所，江西 赣州341000）

0 引 言

高分辨率（high-resolution,HR）图像在遥感监测、视频安全监控、医学MRI（Nuclear Magnetic Resonance Imaging,MRI）和CT（Computed Tomography,CT）影像、视频播放、目标识别与追踪等领域都有广泛的需求[1-3].获取HR的图像，往往对物理成像设备的电子与光学硬件装置有极高要求，因此通过改善硬件装置来获取HR图像的成本较高.图像的超分辨率重建 （super-resolution reconstruction,SRR）是对现有的低分辨率 (lowresolution,LR）图像或图像序列进行信号处理，获得HR图像[2].图像的SRR可在现有物理成像硬件基础上，不增加硬件成本，获得超过成像硬件限制的更高分辨率的图像.

图像的SRR根据图像源个数分为单幅图像SRR和多幅图像SRR.单幅图像SRR主要是恢复图像的高频信息，多幅图像SRR是从一组同场景的LR图像恢复出HR图像[2].在很多没有条件获取一组同场景LR图像序列的情况下，单幅图像SRR就显得尤为重要.此外，单幅图像SRR往往对多幅图像SRR有参考价值.而彩色图像比灰度图像携带更多的信息，更符合人眼对外界感知的实际情况.对彩色图像直接处理，也符合多媒体技术、虚拟现实技术等领域的需求[4].单幅彩色图像SRR的研究工作按照重建时各色彩通道间的关系可分为通道分离重建和通道联合重建两大类.

通道分离重建是彩色图像在各通道上采用单幅灰度图像SRR算法独立进行重建.这些算法主要分为传统插值算法；基于建模的算法，如迭代反投影法[5]、凸集投影法[6]、最大后验概率法[7]等；基于学习的算法，如邻域嵌入法[8]和稀疏表示法[9]等.通道分离重建时，可以根据需求，对不同的通道采用不同的重建算法，大体上可分为三类.

第一类算法，对亮度分量采用基于建模或学习的算法进行SRR，对色度分量进行简单插值；将得到的各通道放大图像融合变换得到HR彩色图像.为了避免颜色失真，这类算法要求通道间低相关，因此通常将通道间高相关的RGB空间转到其他色彩空间，例如HSI空间、YUV空间、HSV空间、YCbCr空间等，然后采用基于建模或学习的算法对亮度分量进行SRR，对色度分量进行简单插值[10].这类算法计算速度虽快，但对色度分量只进行了简单插值，无法利用到先验约束和有用的高频信息，产生的HR图像边缘部分会出现混叠、偏移和模糊等现象，还会造成一定的色彩失真[11].

第二类算法，仍然对亮度分量采用基于建模或学习的算法进行SRR，但将重建后的亮度分量用于指导或约束色度分量的重建[11-12].这类算法能够部分解决色彩失真问题，但在一些亮度分量类似而色度分量截然不同的区域，渗色性将影响重建结果[12].

第三类算法，对亮度分量、色度分量都分别采用基于建模或学习的算法进行SRR.例如2017年Li等[13]在HSV空间上，使用支持向量机作为学习训练工具，通过学习样本库中对应HR与LR图像之间的映射关系，为重建提供指导，从而很好地完成SRR.但在特征向量提取、构造选取混合核函数等方面还可改进，从而进一步获取更准确的HR彩色图像特征.

而通道联合重建是将各通道分量联合稀疏编码或采用四元数联合表示等其他方法表征彩色图像，然后再进行SRR[14-16].这类算法充分考虑了色彩通道间的相关性，从而增加重建图像色彩的逼真度，提高重建质量，并有效弥补了通道分离重建容易造成假色和伪影等不足.通道联合重建主要采用基于学习的算法，重建前期需要训练样本集，重建的效果与性能受限于训练样本的选择机制、算法对训练样本的依赖、算法速度等方面[14].另外，在一些人类还未涉足的地区、航天领域或军事领域进行SRR时，往往无法提供有效的训练样本，而耗时的训练过程也备受诟病.

压缩感知理论自提出以来常被用于图像的超分辨率重建，其中有应用于无训练样本集的情况，如2006年，Sen等[17]在测量前引入高斯低通滤波过程，得到满足等距约束性条件的感知矩阵，然后利用正则化正交匹配追踪算法实现图像在小波域的压缩感知超分辨率重建；也有应用于有训练样本集的情况，如2015年，Sun等[18]先对低分辨率图像双边滤波，然后通过对训练样本集实行K奇异值分解算法，得到冗余字典并对图像稀疏表示，最后实现压缩感知超分辨率重建.一般而言，无训练样本集的方法与有训练样本集的学习方法相比，具有不需要设定训练集、节省前期存储空间和数据运算量的优点.

为了避免大量样本获取和训练耗时的问题，同时考虑到重建后彩色图像的细节特征和色彩保真度，文中提出一种基于形态成分分析（morphological component analysis,MCA）的压缩感知(compressed sensing,CS）彩色图像SRR算法，属于通道分离重建的第三类算法.该算法在不使用外界训练集的情况下，实现单幅彩色图像SRR.首先在低相关的YCbCr色彩空间上，先用MCA的方法对各色彩分量进行分解，对LR的各分量建立伪星形采样的采样方式，然后依据图像不同形态成分的测量值在不同的变换域针对性重建，将得到HR的色彩分量进行线性融合得到最终的HR彩色图像.采用本文算法针对彩色图像进行仿真实验，且将实验结果与传统插值算法和其他MCA相关算法，在客观评价指标和主观视觉体验方面进行比较.本文工作可以看成是曲波变换和快速迭代收缩阈值法的压缩传感超分辨率重建算法[19]，在彩色图像超分辨率重建中方面的推广应用.

1 基于MCA的压缩感知彩色图像SRR

基于压缩感知的SRR的一般思路是将LR图像各通道的信号按照合适的方法稀疏表示，即把信号投影到其他变换域上，将得到的稀疏或近似稀疏的结果看作是原始HR图像信号的采样测量，然后运用重建算法由测量值及投影矩阵重建原始HR图像信号.

信号重构问题可以通过求解最小L0范数问题加以解决，但考虑到最小L0范数问题的NP性，一般转换为最小L1范数优化问题[20].以亮度通道y∈Rn（y分量）为例，从LR图像亮度分量的测量值y′=[y′1，y′2， …，y′M]T恢复重建 HR 图像亮度分量 Y=[Y1，Y2，…，YM]T，可看作求解如式（1）的优化问题：

Φ为测量矩阵 （M×N维矩阵）；Ψ为变换域中的稀疏基（Ψ=[Ψ1,Ψ2,…，ΨN]∈RN，Ψi为 N×1 的基向量）；α 为关于稀疏基 Ψ 的稀疏表示 （α=[α1,α2,…，αN]T∈RN）；ΘM×N为感知矩阵，式（1）求解 α 向量中各元素绝对值之和的最小值，即求解最优的稀疏系数.根据MCA图像分解方法，测量值y′可以用混合基稀疏表示，例如三层MCA稀疏表示为：

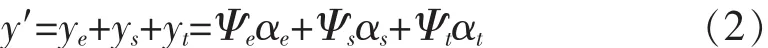
式（2）中：ye为边缘成分；ys为平滑成分；yt为纹理成分；Ψe、Ψs、Ψt分别为对应成分的稀疏基；αe、αs、αt分别为与之对应的稀疏表示.

将式（2）代入式（1），相应的从 LR 测量值 y′恢复重建HR的Y分量，可看作求解如式（3）所示的优化问题：

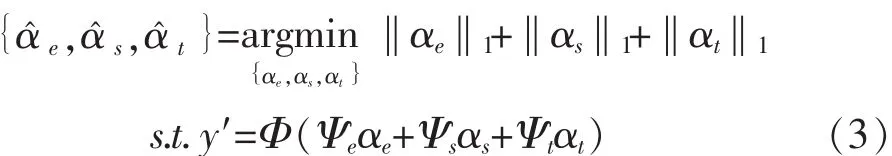
式（3）表示的是一个有条件限制的求极值问题，不易直接实现.为此，加入Lagrange因子，只考虑正则化项η的情况下，则式（3）可近似为无条件约束的优化问题，如式（4）所示：

将其它通道分量按照以上与亮度通道 （y分量）类似的SRR算法进行重建，重建过程主要包括信号的稀疏表示、采样测量和重建算法三个部分，下面针对这三部分做更仔细地论述.

1.1 形态成分分析

形态成分分析是一种基于稀疏表示的信号分解方法，主要思想是利用信号中不同组成成分之间的形态差异性，用不同的稀疏基对各成分进行稀疏表示，最终获得理想的分解效果[21].此外，信号分解后可充分考虑各成分的差异，并进行针对性处理，这比将全部信号作为整体进行处理更为科学，也更接近复杂信号的实际情况.

2010年Jing等[22]利用人类视觉感知和图像梯度特征，将图像根据总变差的方法分解为纹理部分和结构部分，然后采用基于稀疏表示和双三次插值的算法分别重建，进一步融合来实现整个原始LR图像的SRR.2014年胡文谨等[23]将MCA应用到修复唐卡图像领域，采用曲波（Curvelet）变换和局部离散余弦变换 （Local Discrete Cosine Transform,LDCT）分别对图像结构部分和纹理部分进行稀疏表示，采用块坐标松弛算法求解图像修复模型的优化问题.2010年练秋生等[24]将三层MCA应用到图像重构领域，用拉普拉斯塔式分解、圆对称轮廓波和窄带轮廓波变换分别对图像的光滑、边缘和纹理成分进行稀疏表示，采用凸集交替投影算法求解对应的稀疏优化问题实现图像重建.

Curvelet变换不仅具备小波变换的四个特性（稀疏、传播、聚集、方向），还具有另外两个特性（严格采样和各向异性），尤其在方向性上的优势，Curvelet可以表示任意角度，所以在图像的稀疏表示领域中，Curvelet变换能更好地表示图像[25].LDCT是一种典型的局部线性变换，其卷积模板是离散余弦变换块的正交模板，它具有良好的空间域、频率域表征能力，能有效地识别纹理[26].离散平稳小波变换（Discrete Stationary Wavelet Transform,DSWT）是离散小波变换的一种改进，由DSWT每个分解产生的低频和高频部分的尺寸规格等于原始图像尺寸，因此具有平移不变性，可以更有效的表征图像边缘特征[27].故本文用Curvelet变换来表示图像中所占比重较大的平滑成分，DSWT表示图像的边缘成分，LDCT表示图像的纹理成分.本文在文献[21]基础上，实现对y分量进行三层MCA图像分解，具体算法步骤如下：

算法y分量的三层MCA图像分解

输入：y.

输出：ye,ys,yt.

步骤1初始化：迭代次数itermax、正则化参数η、 以及阈值 δ、 停止参数 ε1， 步长 λ=（（δ-ε1））/（（itermax-1）），初始化边缘、平滑部分 ye、 ys为 0，纹理部分 yt=y，αe、αs、αt先置为 0；根据如下步骤迭代itermax次；

步骤2保持ye、ys固定不变，更新yt，首先计算残差 R=（y-Ψeαe-Ψsαs-Ψtαt），然后计算 R+yt，随后对其进行LDCT，最后将变换域系数进行软阈值处理并逆变换获得yt；

步骤3保持ys、yt固定不变，更新ye，首先计算残差 R=（y-Ψeαe-Ψsαs-Ψtαt），然后计算 R+ye，随后对其进行DSWT，最后将变换域系数进行软阈值处理并逆变换得到ye；

步骤4保持yt、ye固定不变，更新ys，首先计算R=（y-Ψeαe-Ψsαs-Ψtαt），然后计算 R+ys，并对其进行Curvelet变换，对变换域系数进行软阈值处理并逆变换得到ys；

步骤 5更新阈值 δ=δ-λ；

步骤6当δ＜λ时，则停止迭代；否则跳到步骤2，直到满足阈值条件；

以Lena图像为例，y分量的三层MCA图像分解结果如图1所示.

图1 彩色图像y分量MCA图像分解

1.2 采样测量方式

对信号做采样测量时，测量矩阵通常为适用于压缩感知的随机投影测量矩阵，例如高斯随机矩阵、伯努利随机矩阵等.在压缩投影和重建过程使用这些随机投影矩阵，面临的问题有：随机数的产生对硬件要求很高；存储和传输这些测量矩阵，对系统要求也很高；随机测量矩阵只在数学统计意义下，使得Θ大概率满足约束等距性和弱相干性，而每次生成的随机Φ不能完全保证Θ满足上述条件，故影响后续精确恢复HR图像[28].

采用构造的确定性测量矩阵，如星形测量矩阵、双星形测量矩阵、星形环状测量矩阵均可有效地完成压缩感知重建过程[29].在此基础上改进的伪星形测量矩阵可有效利用原有的LR图像的全部信息和部分插值后的HR图像有效完成SRR[19].

对y分量包含的各成分都采用这种伪星形采样测量方式，以纹理成分yt为例，超分辨率伪星形测量矩阵的采样方式[19]具体算法步骤如下：

算法超分辨率伪星形测量矩阵的采样方式

输入yt.

输出 Yt′.

步骤1采用双立方插值将LR的yt放大到目标倍数，得到 HR 的 yt′；

步骤2对yt′进行二维快速傅里叶变换（fft2）并重排系数，把低频信息移动到频谱图中心；

步骤3 yt进行fft2，并重排傅里叶系数，把低频信息移动到频谱图中心；

步骤4将步骤2中的频谱图中心维数与yt相同的区域用（3）中的低频频谱图取代，得到 yt′′；

步骤5按照yt′′的维数建立星形采样矩阵；

步骤6将星形采样矩阵的中心，维数与yt相同区域置为1，即构造出伪星形采样矩阵；

步骤7伪星形采样矩阵与yt′′相乘；

步骤8对步骤7的处理结果逆重排系数后，逆FFT2后得到y分量纹理成分的超分辨率测量值Yt′.

其他分量同样采用这种超分辨率伪星形测量矩阵的采样方式，具体采样过程如图2所示.

图2 超分辨率伪星形测量矩阵的采样方式

1.3 恢复重建算法

重建算法在这里是指由y分量纹理成分yt的测量值Yt′重建 HR纹理成分图像 Yt的过程.常见的重建算法主要有匹配追踪算法、迭代阈值法等.考虑到平滑部分Curvelet基的冗余性，如采用匹配追踪重建则需构造高维的稀疏矩阵和测量矩阵，采用迭代收缩阈值算法可解决此问题.为提高重建效率，文中采用一种快速迭代收缩阈值法[30-31]（A Fast Iterative Shrinkage-Thresholding Algorithm,FIST）进行恢复重建，它在每一步迭代中计算近似函数的起止点时，使用前两次迭代过程的结果αtk和αtk-1对其进行简单的线性组合生成下一次迭代的近似函数起始点αtk+1，具体可描述为：

式（5）中，参数pk用来根据前两次变换域系数αtk和αtk-1来确定新的变换域系数αtk+1，参数pk的初值p1为1，其更新算法具体为：

FIST对初值非常敏感，所以很难直接应用于信号重构.但如果能找到一个合适的初值，迭代算法就可找到全局最优解.故本研究采用1.2节中的方式进行采样测量，变换后获得一个具有一定指导意义的初值αtk，然后结合LDCT对最优变换域系数αtk+1进行迭代更新，再经LDCT逆变换即得y分量纹理成分的时域图像Yt.具体算法步骤如下：

算法 基于LDCT和FIST结合的压缩感知重建算法

输入 Yt′.

输出Yt.

步骤1初始化：设定迭代停止参数ε2，迭代系数 γ， 阈 值 σ=max_e*η （max_e是 LR图 像 经Bicubic放大后LDCT变换系数中的最大值，η为正则化因子），收缩因子μ，迭代次数k，采用1.2节中的方式对LR图像采样测量得到yt，初始化 Xtk=yt；

步骤 2对测量图像 Xtk进行 LDCT，αtk=ΨXtk；

步骤 3 计算残差 R=αtk-αtk-1；

步骤 4 迭代更新：αtk+1=αtk+γ*R；

步骤5更新 ttk+1与αtk+1；

步骤6软阈值处理αtk+1；

步骤 7进行 LDCT逆变换：Xtk+1=ΨTαtk+1；

步骤 8 软阈值松弛：σ=σ*μ；

步骤9当σ＜ε2时，则停止迭代；否则跳到步骤2，直到满足阈值条件，即得到重建的y分量纹理成分图像Yt.

在上述基于LDCT和FIST结合的压缩感知重建算法（LDCT-FIST）中，LDCT可替换为DSWT或Curvelet变换，亦可实现基于DSWT和FIST结合的压缩感知图像重建算法（DSWT-FIST）和基于Curvelet变换和FIST结合的压缩感知重建算法（Curvelet-FIST），用来求解 αek+1、αsk+1，从而得到Ye和Ys分量，可并行处理，具体过程如图3所示.

2 实验结果与分析

图3 基于MCA的压缩感知彩色图像超分辨率重建流程

在Windows10系统下使用MTALAB R2016b软件为仿真实验测试环境，从SIPI Image Database的misc标准测试图像中，选取了Lena、Badoon、Pepper、Lady四幅，并预处理为维数256*256*3的YCbCr色彩空间的图像，作为HR原图.4幅原图分别属于人类、动物、植物、油画的类别.

测试时将HR原图降采样为128*128*3的LR图像，并依次采用以下五种算法进行放大2倍的SRR.算法一对YCbCr色彩空间的各通道分量，使用Bicubic插值重建，记为Bicubic；算法二对YCbCr色彩空间的各通道分量，使用基于Curvelet变换的压缩传感超分辨率重建方法进行重建[19]，记为Curvelet-FIST；算法三将YCbCr色彩空间的各通道分量，分解为结构层和纹理层，采用压缩感知的算法对各分量重建，记为MCA2-CS；算法四的分解过程与本文相同，采用三层MCA分解彩色图像，对各分量进行Bicubic插值重建，记为MCA3-Bic；算法五为本文算法，记为Ours，采用三层MCA分解彩色图像，并采用压缩感知的算法对各通道分量重建.在重建彩色图像的各通道分量后，这五种算法都采用相同的融合方式来形成最终的HR彩色图像.

重建效果评价采用峰值信噪比 （Peak Signal Noise Ratio,PSNR）和结构相似指数（Structural Similarity Index Measurement,SSIM）来衡量，其中，PSNR为最常用的评价指数，它的计算公式为：

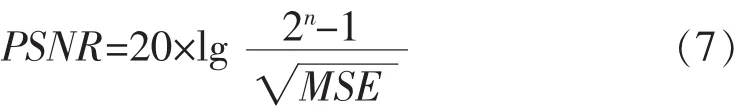
式（7）中，n为像素的比特数，MSE的计算公式为：

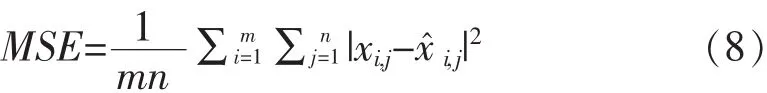
式（8）中：m,n 为图像的长和宽；xi,j为点（i，j）的原始像素值；x^i,j为点（i，j）重构后的像素值.

SSIM则是从图像组成的角度将结构信息定义为独立于亮度、对比度、反映出场景中物体结构的属性，并将失真建模为亮度、对比度和结构三个不同因素的组合[32].用均值作为亮度的估计，标准差作为对比度的估计，协方差作为结构相似程度的度量.计算公式为：

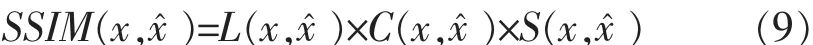
其中，L（x，x^）、C（x，x^）、S（x，x^）的计算公式分别为：

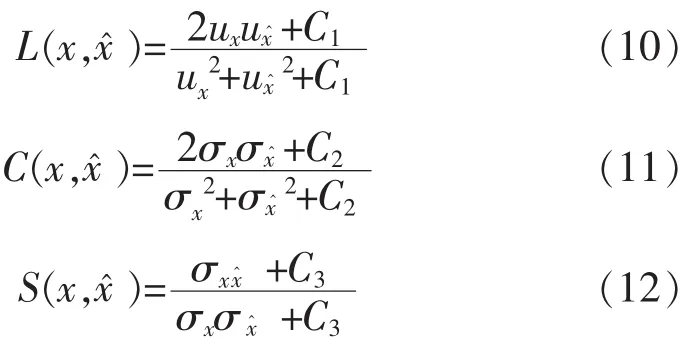
其中，ux、ux^分别 x、x^的均值，σx、σx^分别为 x、x^的标准差，σx2、σx^2分别为 x、 x^的方差，σxx^为 x和x^协方差，C1、C2、C3为常数. 为了避免分母为零而维持稳定， 通常取 C1=（K1×L_max）2、 C2=（K2×L_max）2、C3=C2/2， 一般 K1取 0.01，K2取 0.03，L_max 是像素值的取值范围，此处取255.

当C3=C2/2时，上式可简写为：

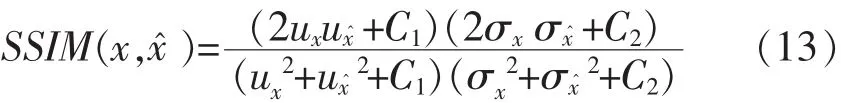
重建过程中，将重建的HR图像的每个通道分量都与原图的通道分量进行对比，计算了每个通道分量的PSNR和SSIM，作为图像重建过程的客观评价指标，如表 1、表 2中的 Y、Cb、Cr列所示.此外，为了比较彩色图像重建的整体效果，还针对每幅彩色图像，计算了三个彩色通道的PSNR的平均值和SSIM的平均值，计算结果如表1、表2中的AVG列所示.此外将原图转为灰度图，并将重建后的彩色图像按同样方法也转为灰度图像，并进行比较，计算的PSNR值和SSIM值如表1、表2中的GRAY列所示，此结果从另一角度反映了彩色图像的整体重建效果.

表1 重建图像的PSNR值/dB

表2 重建图像的SSIM指数

对比表1中AVG列的PSNR值发现，除了Lady图，在其余3幅图像结果中，都是本文算法最高，平均 PSNR值依次为 40.65 dB、34.06 dB、38.98 dB；而对于Lady图，本文算法的平均PSNR值为41.21 dB，低于算法一，但高于算法二、算法三和算法四.而在表1中GRAY列的PSNR值中，本文算法的具体数值依次为 34.81 dB、30.03 dB、35.36 dB、36.11 dB，与其余四种算法相比都更高.

在表2中，虽然对于Lady图的Y分量而言，本文算法的PSNR值为0.9081，略低于算法一，且高于算法二、算法三和算法四，但对于其余分量的结果以及体现重建综合效果的AVG列的SSIM指数、GRAY列的SSIM指数，都是本文算法的结果最高.

综合对表1、表2的数据分析可知，本文算法的整体重建效果优于其他4种算法.

表1、表2客观反映本文方法在色彩方面的重建优势，为了从人眼角度更主观地对比前述5种不同算法的SRR效果，以Lena图像的SRR结果为例，将其转化到RGB色彩空间并显示出来，如图3所示，其中图 4（a）为降采样的 Lena 图像，图 4（b）至图4（f）是将图4（a）经五种不同算法的SRR得到的结果，图 4（g）为原图.

对比发现，本文算法重建的图像不管从整体和细节上都得到了很好的改善，更加平滑自然，得到了很好的还原.其中图4（b）在Lena的发梢、肩膀处有明显的边缘模糊和混叠现象；图4（c）虽有所改善但仍存在此类问题；图4（d）在发梢处明显改善，但仍有个别细节处有模糊现象；图4（e）比图3（d）的重建结果略好，而文中算法在重建图像的色彩保真度和图像形态成分的重建效果显然更好，主观评判整体效果也更为出色.

图4 Lena图像SRR重建效果对比

以Lena图像的SRR结果的发梢、帽子、肩部三个细节为例，选用重建综合效果较好的三种算法对重建图像的细部进一步对比.RGB色彩空间显示的重建图像细部如图5所示，其中图5（a）、图5（e）、图 5（i）为 MCA2-CS 算法得到的细节结果图，图 5（b）、图 5（f）、图 5（j）为 MCA3-Bicubic 算法得到的细节结果图，图 5（c）、图 5（g）、图 5（k）为本文算法得到的细节结果图，图 5（d）、图 5（h）、图 5（l）为原始图像细节部分.通过人眼与原图细节部分进行主观对比，与各算法重建的细部对比发现，图5（c）发梢处细节信息、图 5（g）帽子处纹理信息、图 5（k）肩部的边缘信息和平滑低频信息的恢复效果明显更好.

图5 Lena局部细节图

3 结 论

目前彩色图像SRR算法中的基于学习的重建算法需要大量的训练样本，存在大样本获取和训练耗时等问题，而传统的插值算法重建效果不佳，会造成色彩失真、边缘模糊和混叠等现象.文中针对这些问题，提出一种基于MCA的压缩感知彩色图像SRR算法.该算法在不使用外界训练集的情况下，先将色彩分量分解为不同形态成分，然后根据各成分差异进行针对性重建，最终实现单幅彩色图像SRR，一方面大幅度节省了大量样本获取和训练的时间，另一方面由仿真实验结果可知，该算法较传统插值算法、两层MCA的压缩感知SRR算法以及三层MCA的双立方插值算法，客观评价指标与主观视觉效果均有提高，重建效果较好.