褶皱结构对蜻蜓后翅的气动特性影响分析

罗云，何国毅，王琦，宋航，陈冬慧

(南昌航空大学 飞行器工程学院，南昌 330063)

0 引 言

蜻蜓堪称有翼昆虫界的战斗机，具有优异的飞行本领，是微型扑翼飞行器最合适的仿生对象。蜻蜓通过振动翅膀，产生不同于周围大气的局部不稳定气流，利用气流产生的涡流上升，能在很小的推力下翱翔[1]，甚至可以在几乎不消耗能量的情况下滑翔很长一段距离。蜻蜓高超的飞行能力更体现在它不但可以向前、后、左、右各个方向飞行，还可以进行急转、俯冲、空中悬停等高难度动作，甚至能够短距离上下垂直飞行[2]。蜻蜓飞行常表现为拍动、滑翔和悬停等姿态，尤其是在炎热天气时，滑翔飞行更是蜻蜓最常采用的飞行方式。滑翔飞行不仅可以降低翅膀的扑动频率，减少能量消耗，还可以利用空气对流等方法进行体温调节[3]。此外，蜻蜓单个翅膀的展弦比约为5[4]，远大于其他昆虫，可通过消耗很少的能量得到较好的滑翔飞行能力。

目前大多数的实验研究和数值模拟计算中，人们常将蜻蜓翅膀简化为一个仅具有翅膀外轮廓的平板模型，然而在对蜻蜓翅膀形态和结构的研究中，已经证明蜻蜓翅膀结构复杂，看似一个二维平面结构,实际上是一个空间立体三维褶皱结构。蜻蜓翅膀主要由翅膜和翅脉组成，翅膜是蜻蜓翅膀的主要空气动力学结构，厚度仅为0.04 mm[5]。翅脉是中空圆管结构，又可分为纵脉和横脉，并且纵脉和横脉交织分布形成的脉络结构，是蜻蜓翅膀的主要承载结构。另外，蜻蜓翅膀横截面的形状沿展向上呈褶皱状，整个横截面上的厚度也有细微差异[6]。这种褶皱结构已经被证明能够在减轻蜻蜓翅膀重量的同时，有效改善其应力分布，提高弯曲刚度和挠性，保持蜻蜓翅膀飞行时的稳定性[7-8]。

然而，褶皱结构是否能对蜻蜓翅膀的气动性能产生正面的影响仍存在争议。R.H.Buckholz[9]在对蜻蜓褶皱结构的实验研究中发现，褶皱结构可以降低蜻蜓翅膀的阻力、提高升力，使其拥有较好的气动性能，A.Vargas等[10]的理论计算研究也得到了相似的结果。相反，C.J.C.Rees[11],B.G.Newman[12]和R.Rudolph[13]的风洞实验证明，褶皱结构仅能够推迟大攻角下涡的脱落，并不能改善其空气动力学性能。X.G.Meng等[14]的计算研究也表明褶皱结构具有降低蜻蜓翅膀升力的作用。

不同于其他四翼昆虫，蜻蜓飞行时，其前、后翅既是相互独立又是相互影响的。滑翔飞行时，蜻蜓既可以只振动一对前翅，而将后翅伸展；也可以同时伸直前、后翅进行滑翔[15]。目前对蜻蜓前翅的研究较多，但是对蜻蜓后翅和蜻蜓前、后翅共同作用的研究却寥寥无几。

本文在蜻蜓后翅实际结构特征的基础上，做适当简化，建立接近真实蜻蜓后翅的三维蜻蜓后翅褶皱模型和拥有同样外形的三维平板模型，利用计算流体力学方法分别计算两个模型在不同Re、不同α下滑翔飞行时的气动特性，以探究褶皱结构对蜻蜓后翅气动性能的影响及与Re的相关性。

1 模型和方法

1.1 控制方程

三维不可压无量纲化的N-S方程如下：

(1)

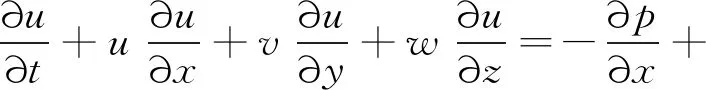
(2)

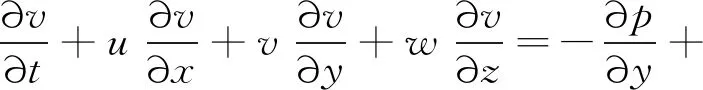
(3)

(4)

式中：u,v,w分别为速度沿x,y,z方向的分量；p,t为压强和时间，Re为雷诺数。

(5)

式中：ρ,U和μ分别为自由流的密度、速度和动力粘性系数；c为蜻蜓后翅的平均弦长。

对蜻蜓翅膀气动性能优劣判断的主要依据为其升力系数和阻力系数，定义分别为：

(6)

(7)

式中：F1为升力；Fd为阻力。

流体控制方程是以SIMPLE算法，采用SSTk-ω模型，通过商业软件STAR-CCM+计算完成。

1.2 几何模型

根据蜻蜓后翅的实际结构特征，本文对三维蜻蜓后翅褶皱模型做出如下四点简化：①不同姿态滑翔时，后翅可能处于前翅的尾流区，其气动特性会受到影响，故忽略滑翔时蜻蜓前翅尾流对蜻蜓后翅气动特性的影响；②不考虑蜻蜓后翅在气动载荷作用下的变形，假设该模型为刚性，忽略柔性对其气动特性的影响；③忽略翅痣和翅结等对其气动特性影响较小的结构；④翅脉和翅膜沿展向和弦向的尺寸变化主要对蜻蜓后翅结构方面的影响较大，故忽略翅脉和翅膜沿展向和弦向的尺寸变化，将翅脉简化为厚度为0.18 mm的中空圆管，翅膜的厚度为0.04 mm。

三维蜻蜓后翅褶皱模型的建立过程如图1所示：在建模软件CATIA中导入蜻蜓后翅的几何结构图，利用样条曲线描绘蜻蜓后翅轮廓，如图1(a)所示；填充后翅轮廓形成的翅膜面，参考文献[6]中实验所得的四个横截面,通过实际测量各截面翅膜的偏转角度来偏转翅膜面，形成蜻蜓后翅的褶皱结构，如图1(b)所示；在对应翅脉的样条曲线上建立空心圆管状翅脉，并且赋予翅脉和翅膜不同的厚度，形成厚度为0.04 mm的翅膜结构、厚度为0.18 mm的中空圆管状翅脉以及脉络结构，如图1(c)所示，其中1为中空圆管状翅脉，2为形状各异的翅膜，3为翅脉形成的脉络结构；三维蜻蜓后翅褶皱模型如图1(d)所示，其中a～d为蜻蜓后翅展向不同位置的褶皱结构。

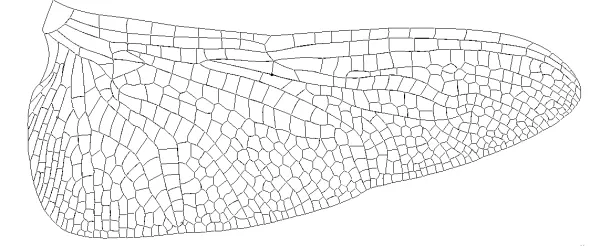
(a) 蜻蜓后翅轮廓

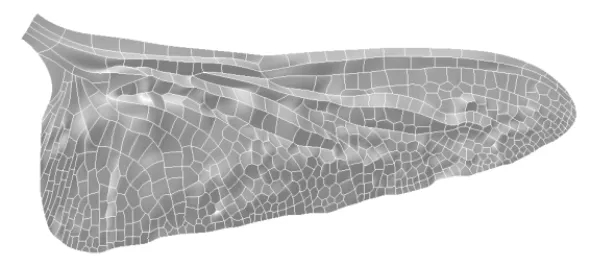
(b) 翅膜面偏转结构示意图

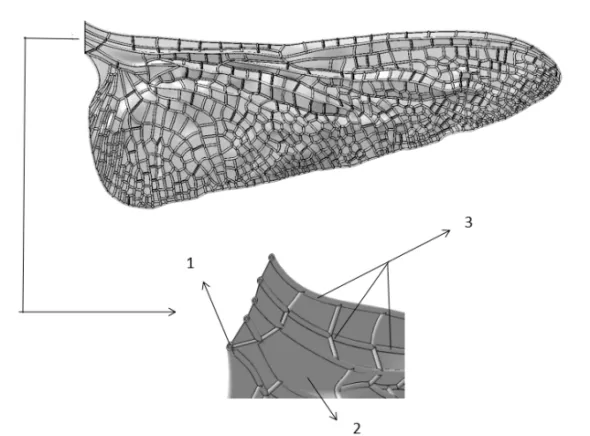
(c) 中空圆管状翅脉以及脉络结构

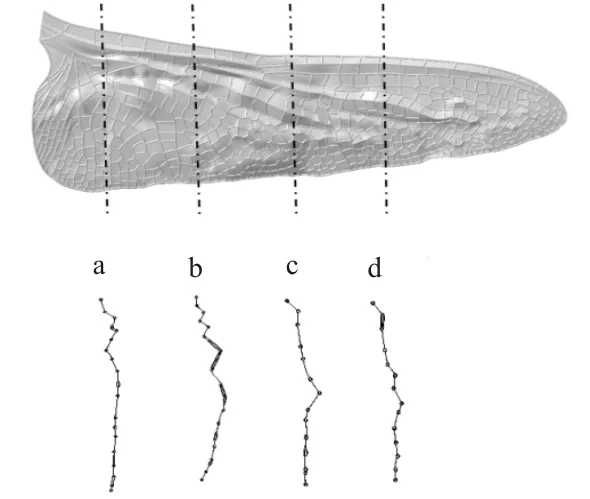
(d) 三维蜻蜓后翅褶皱模型

为了探究褶皱结构对蜻蜓后翅气动效能的影响，建立拥有同样外形的三维平板模型作为对照组。三维平板模型与三维蜻蜓后翅褶皱模型的外形相同，参考面积相同，厚度也与蜻蜓后翅翅脉的外径尺寸一致，为0.18 mm，并且对三维平板模型的外缘做圆弧处理，如图2所示。

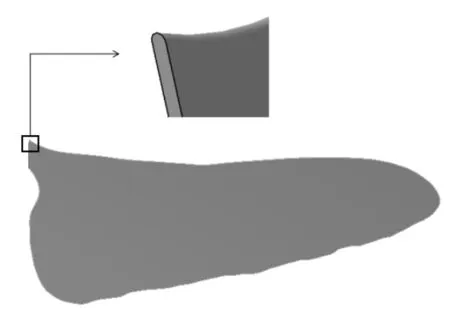
图2 三维后翅平板模型

1.3 计算流域与边界条件

建立计算流域，由前、后、左、右、顶部和底面六个面组成，尺寸如图3所示(其中L为展长)。

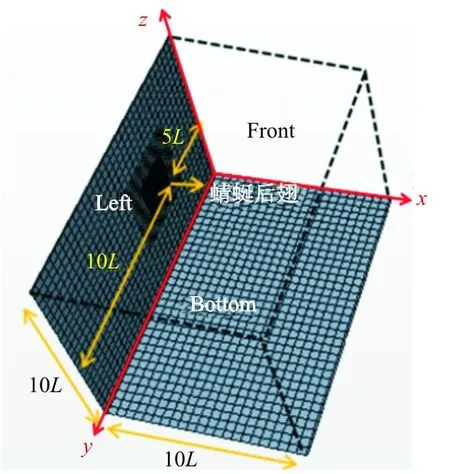
图3 计算流域

三维蜻蜓后翅褶皱模型的翼根处所在平面(即左面)的边界条件设置为对称面，后翅的边界条件设置为壁面。

1.4 网格无关性验证

为了排除网格尺寸对计算结果的影响，在Re=10 000，α为0°的情况下，计算了多组不同网格尺寸的网格模型。计算结果表明：当网格数量为973万个时，蜻蜓后翅的升力系数为0.196，当网格数量增加至1 375万个甚至更多时，升力系数基本维持在0.187，此时可以认为当网格数量大于等于1 375万个时，计算结果与网格数量无关，网格无关性验证趋势如图4所示。权衡计算效率与计算结果的准确性，最终选用网格数量为1 375万个，即网格尺寸为0.04 mm的网格模型作为求解模型，局部模型网格如图5所示。

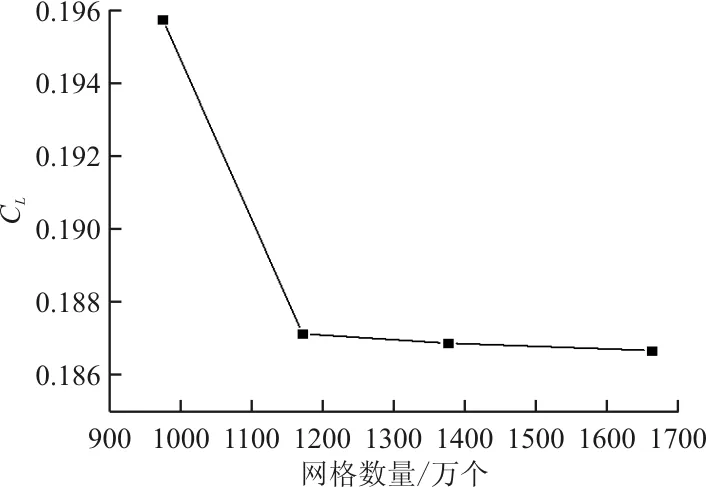
图4 网格无关性验证趋势图

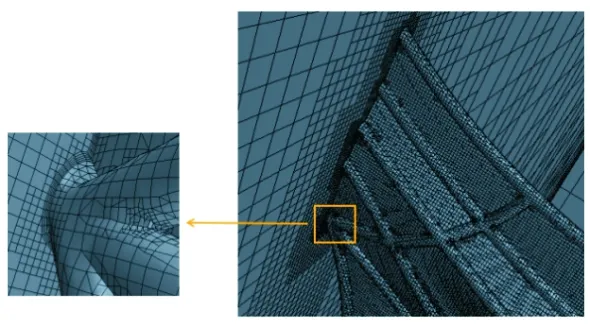
(a) 三维蜻蜓后翅褶皱模型

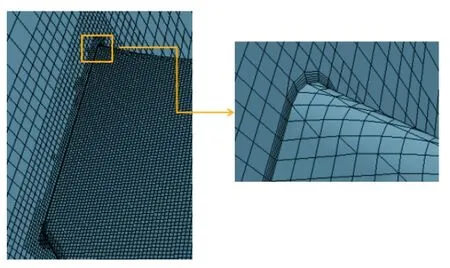
(b) 三维平板模型

2 结果与分析

2.1 相同Re情况(Re=10 000)

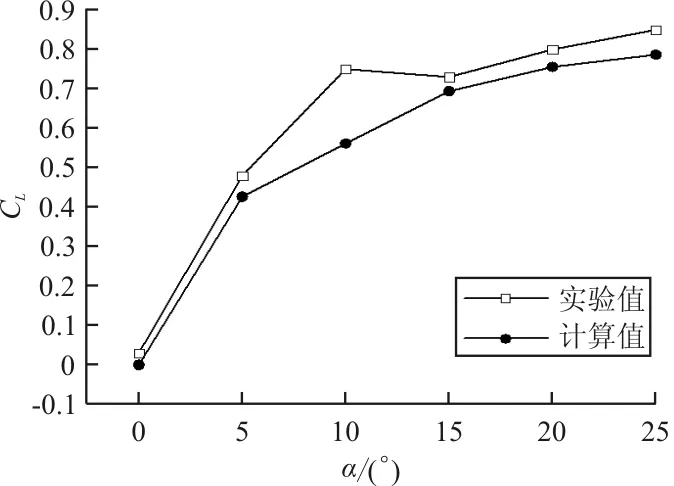
KESEL[3]在Re=10 000的条件下对多种具有褶皱结构的翼型剖面和相对应的平板模型进行了实验研究，得到了相应的升、阻力系数实验值。本文为了探究滑翔时褶皱结构对蜻蜓后翅气动效能的影响，首先计算了Re=10 000时，三维平板模型和三维蜻蜓后翅褶皱模型分别在α介于0°～25°时(α间隔为5°)滑翔飞行的升、阻力系数。

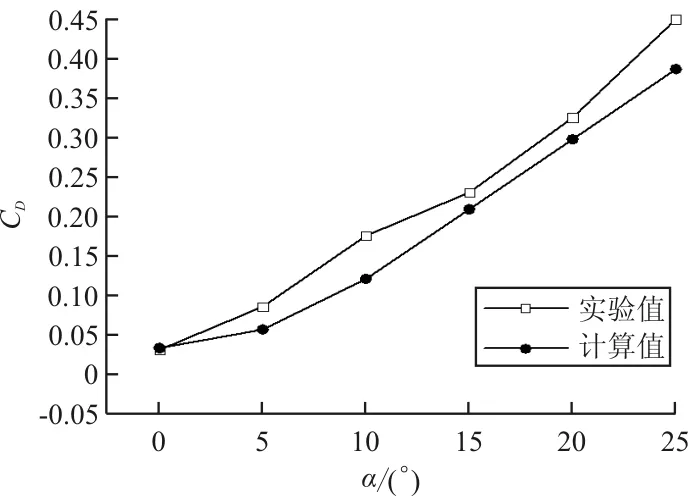
三维平板模型的计算值与KESEL[3]实验值的升、阻力系数对比曲线图(Re=10 000,α=0°～25°，α间隔为5°)如图6所示。

(a) 升力系数

(b) 阻力系数

从图6可以看出：实验值和计算值的升、阻力系数的整体趋势是一致的，并且实验值的升力系数和阻力系数均略大于计算值，原因可能是存在一定的实验误差与计算误差。

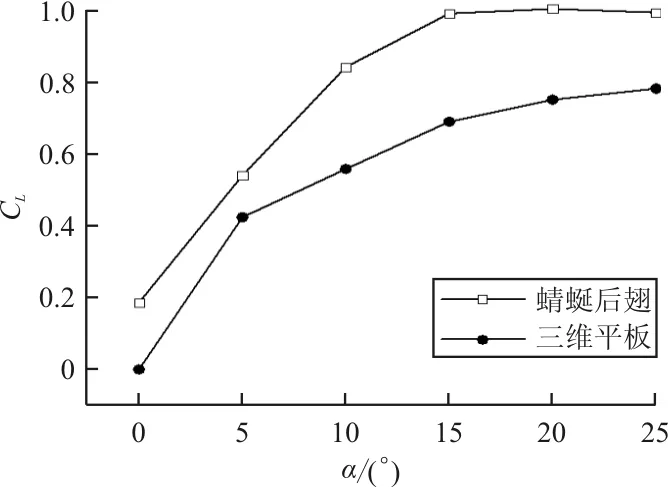
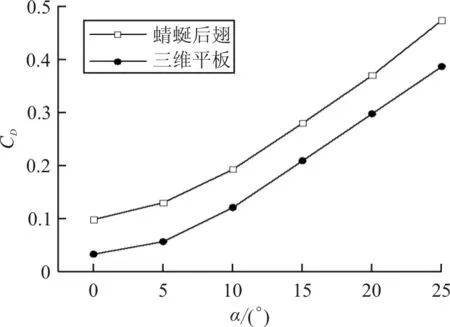
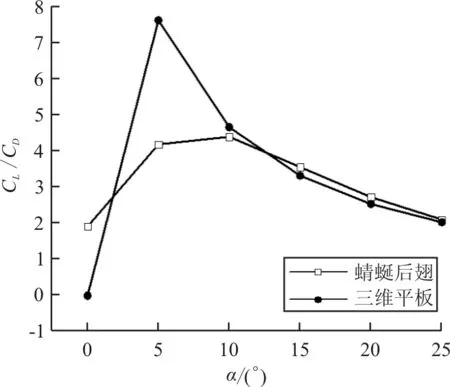
三维蜻蜓后翅褶皱模型和三维平板模型的升、阻力系数计算值的对比曲线图(Re=10 000,α=0°～25°，α间隔为5°)如图7所示。

(a) 升力系数

(b) 阻力系数

(c) 升阻比

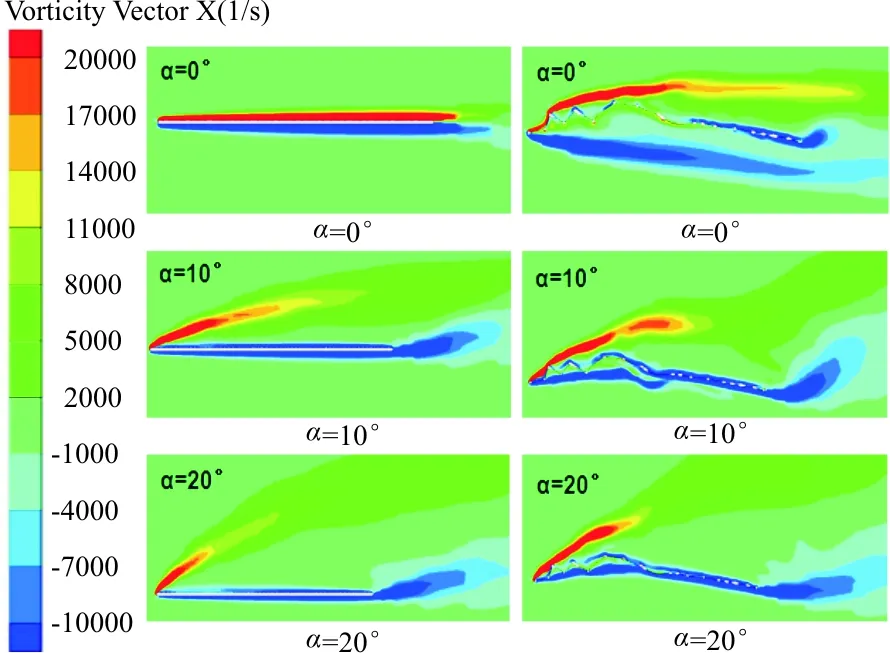
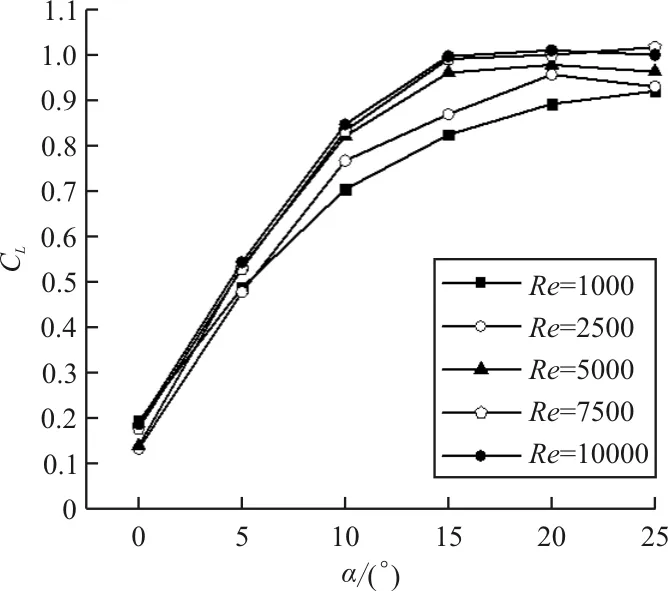
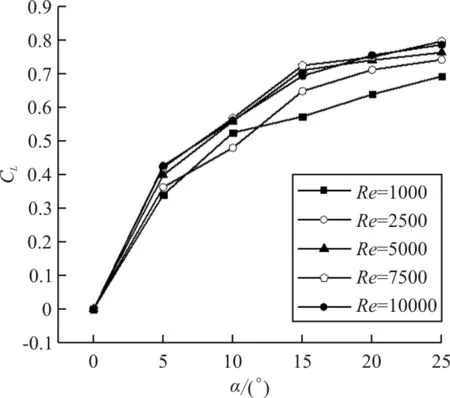
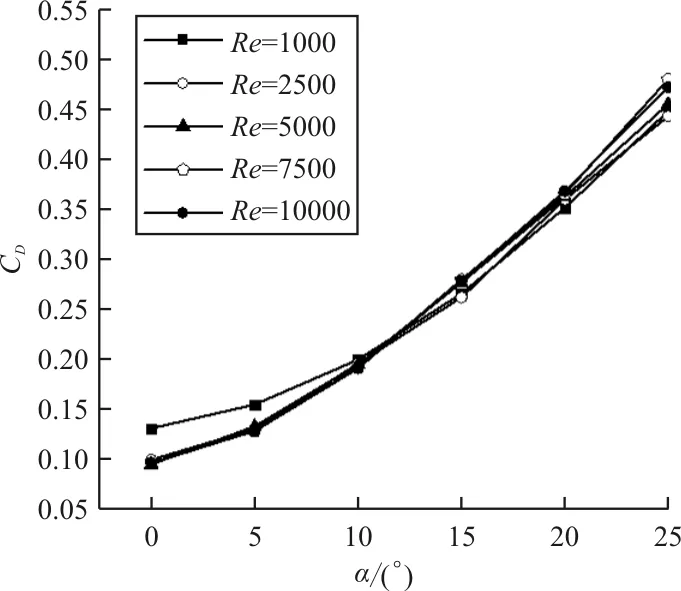
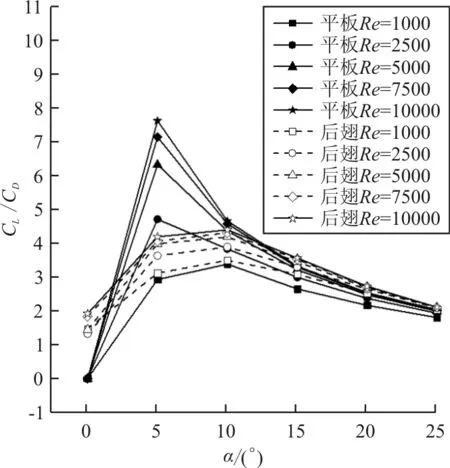
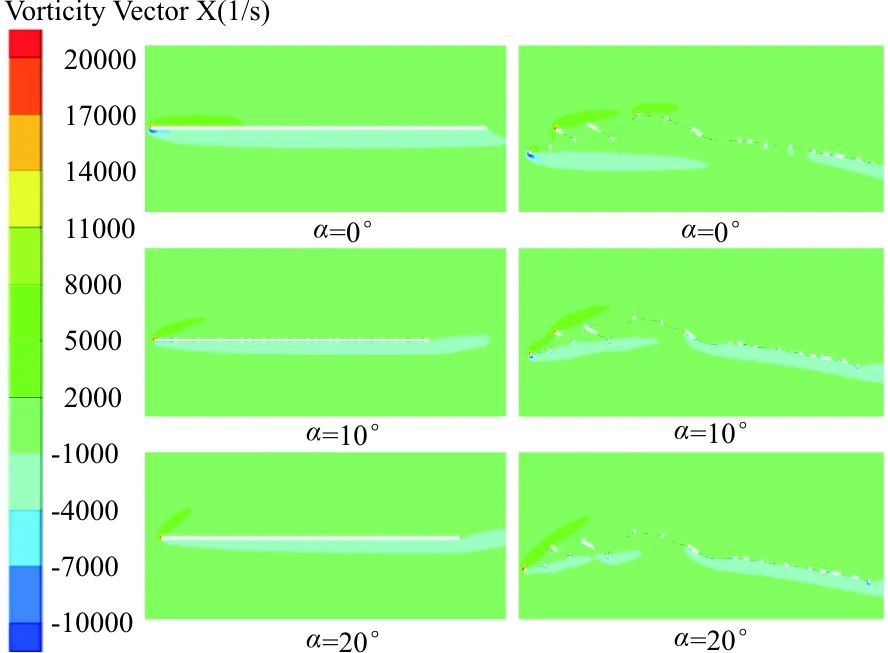
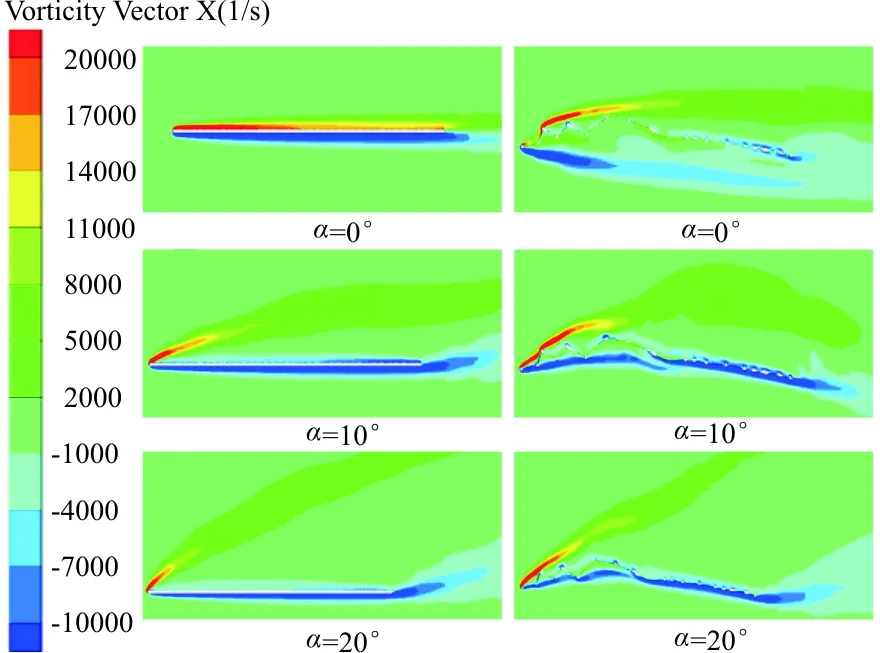
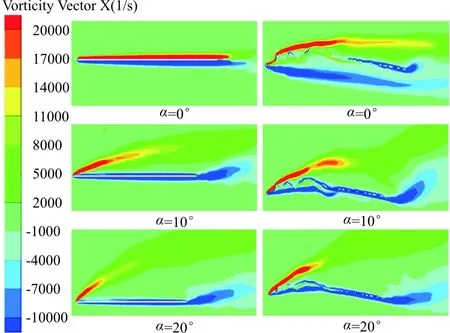
从图7(a)可以看出：α=0°～25°时，蜻蜓后翅的升力系数明显大于三维平板，并且α=0°时，三维平板的升力系数为零，而蜻蜓后翅的升力系数为0.19。蜻蜓后翅的升力系数随α(α=0°～25°，α间隔为5°)增加的增长率分别为65.6%、35.9%、15.0%、1.30%、-1%，α=15°～25°时，蜻蜓后翅升力系数增长速度明显下降；α=0°～25°时，三维平板的升力系数随攻角增加的增长率分别为24.0%、19.1%、8.2%、3.9%。从图7(b)可以看出：α=0°～25°时，蜻蜓后翅与三维平板的阻力系数增长趋势一致，并且蜻蜓后翅的阻力系数计算值均大于三维平板；从图7(c)可以看出：0°≤α≤10°时，三维平板的气动效能明显优于蜻蜓后翅；10°

三维蜻蜓后翅褶皱模型0.2L(L为展长)截面处的流线图(α=20°,Re=10 000)如图8所示。

图8 蜻蜓后翅0.2L(L为展长)截面处的局部流线放大图(α=20°,Re=10 000)

从图8可以看出：褶皱结构上下表面的凹槽结构均被驻留涡填充，并且上表面的驻留涡为顺时针旋转，下表面呈逆时针旋转，与C.J.C.Rees[11]、刘惠祥等[15]人二维褶皱结构的计算结果一致。一方面，驻留涡填充了褶皱结构上下表面的凹槽，使得其流动与光滑流线翼型的流动相似；另一方面，上下表面的驻留涡沿不同方向旋转，使得褶皱结构的压差阻力大于三维平板，从而使得褶皱模型的阻力系数均大于三维平板。

三维平板模型和三维蜻蜓后翅褶皱模型分别在0.2L(L为展长，Re=10 000)截面处的涡量图如图9所示，可以看出：滑翔飞行时，蜻蜓后翅和三维平板的前缘处均产生了一个较强的前缘涡，并且两个模型的前缘涡均随α的增大而逐渐减小；当α相同时，蜻蜓后翅的前缘涡要大于三维平板，而且随着α的增大，尤其在较大α情况时，蜻蜓后翅的前缘涡更明显的要强于三维平板。前缘涡是蜻蜓翅膀产生升力的重要原因之一，相较于三维平板，蜻蜓后翅的褶皱结构能够诱导出更强的前缘涡，并且这种诱导作用随着α的增大而越发明显。

图9 三维平板和蜻蜓后翅0.2L(L为展长)截面处的涡量图(Re=10 000)

2.2 不同Re情况(Re=1 000～10 000)

目前对蜻蜓翅膀褶皱结构的研究发现，滑翔飞行时，蜻蜓翅膀Re的量级一般为102～104。A.Vargas等[10]在α为5°时，对蜻蜓翅膀褶皱结构在Re为500,1 000,5 000和10 000时的气动特性进行了理论计算研究。研究表明Re=10 000时，褶皱结构能够提高蜻蜓翅膀的升力，但Re为其他数值时，褶皱结构的升力均比相对应的平板小。为了探究滑翔时褶皱结构对蜻蜓后翅气动效能的影响是否与Re相关，本文计算了三维平板模型和三维蜻蜓后翅褶皱模型Re为1 000,2 500, 5 000,7 500和10 000时滑翔飞行的升力系数与阻力系数(α=0°～25°，α间隔为5°)。

三维蜻蜓后翅褶皱模型与三维平板模型在Re介于1 000～10 000时(α=0°～25°，α间隔为5°)的升、阻力系数计算值对比曲线图如图10所示。从图10(a)和图10(b)可以看出：随着Re的增大，蜻蜓后翅和三维平板的升力系数均明显增大，并且在较大α情况时，升力系数随Re的变化更明显；但是当Re增大到一定值时，其升力系数的大小几乎不再随Re的增大而增大。从图10(c)和(d)可以看出：Re=1 000时，α较小的情况下，蜻蜓后翅和三维平板的阻力系数均明显要大于其他Re情况。当Re≠1 000时，在计算的所有α情况内，阻力系数几乎不随Re的变化而变化。从图10(e)可以看出：Re=1 000，α=0°～25°时，蜻蜓后翅的气动效能始终略优于三维平板。当Re≠1 000时，本文计算的其他雷诺数情况下，褶皱结构对蜻蜓后翅气动性能的影响与α相关：α较小时，三维平板的气动效能明显优于蜻蜓后翅；α较大时，蜻蜓后翅的气动效能略优于三维平板。

(a) 蜻蜓后翅升力系数

(b) 三维平板升力系数

(c) 蜻蜓后翅阻力系数

(d) 三维平板阻力系数

(e) 升阻比随Re的变化曲线

不同雷诺数下三维平板模型和三维蜻蜓后翅褶皱模型在0.2L(L为展长)截面处的涡量图如图11所示。

(a) Re=1 000

(b) Re=5 000

(c) Re=10 000

从图11可以看出：同一Re情况下，蜻蜓后翅和三维平板的前缘涡均随α的增大而逐渐减小，并且当α相同时，蜻蜓后翅的前缘涡总大于三维平板的前缘涡；Re不同时，蜻蜓后翅和三维平板的前缘涡均随Re的增大而增大。

3 结 论

滑翔飞行时蜻蜓后翅和三维平板的前缘处均产生了一个前缘涡，并且两个模型的前缘涡均随 的增大而逐渐减小；相较于平板结构，褶皱结构的存在可以诱导出更强的前缘涡，从而使三维后翅褶皱模型的气动特性优于平板结构；在不同Re下滑翔飞行时，褶皱结构对蜻蜓后翅气动特性的影响有所不同，较小Re情况时蜻蜓后翅的气动特性略优于三维平板。

褶皱结构的存在可以让蜻蜓在滑翔飞行时拥有更好的气动性能，当设计仿生扑翼微型飞行器时可以考虑采用褶皱结构来代替传统的平板结构，为设计性能更优的微型飞行器提供一定的参考依据。