缝翼结构参数对翼型流场和气动噪声的影响

王红建，罗望，张锐

(西北工业大学 航空学院，西安 710072)

0 引 言

民用航空的快速发展带来日益严重的噪声问题，引起各国航空制造企业与研究学者的关注。国际民航组织(ICAO)制定严格的噪声适航条例来限制民航飞机的噪声[1-2]。欧洲航空研究咨询委员会(ACARE)与美国国家航空航天局(NASA)都制定相应的研究计划以降低民航飞机的噪声水平[3-4]。我国的商用大飞机研制刚刚起步，降低飞机噪声水平不仅可以满足适航要求，而且对提高飞机竞争力有着重要作用。

飞机噪声主要由发动机与机体的噪声组成[5-6]。前者在早期的民航飞机中占主导地位，但随着先进涡轮发动机的研制，尤其是大涵道比涡扇发动机的应用，其噪声水平已经大幅降低。因此对机体噪声水平抑制的研究逐渐变得重要起来。

研究表明[7-9]，在民航客机起飞和着陆过程中，机体噪声的主要来源为起落架和增升装置。其中，前缘缝翼噪声是增生装置噪声的主要部分[1,10]。降低缝翼噪声对机体噪声的减小有重要意义。然而，缝翼为增升装置的一部分，对其噪声的控制可能会对增升性能带来不利影响，因此有必要对其降噪方法及其对升力的影响进行细致的分析。

缝翼噪声源主要由缝翼凹腔处复杂的湍流流动引起[11-12]，减小由缝翼凹腔处湍流流动引起的噪声势必对总体噪声的降低做出重要贡献。为实现这一目标，国内外学者均进行一系列的研究，主要思想为通过主/被动技术来减弱或消除凹腔处回流以及涡流与再附着位置的碰撞。主动技术主要是通过吸/吹气及等离子体控制等方法来降低噪声源强度。如在缝翼压力面上布置吸气槽来抽出缝翼凹腔的回流气泡，以减弱凹腔内的湍流强度[13-14]，进而降低远场噪声辐射；在缝翼尾缘吸力面向外喷气，可对大于2 kHz的噪声有一定的削弱[15-16]；在靠近缝翼尖端(Cusp)的吸力面施加等离子体控制，可削弱窄带噪声[17]等。被动技术主要采用封闭、填充(Slat Sove Filler，简称SCF)及铺设声衬材料等方法来减小甚至消除噪声源：如封闭缝道可以消除凹腔流动，从而显著降低缝翼宽频噪声[18]；采用SCF改变不连续缝翼尖点处的外形[19-24]，使剪切层在尖点处受到抑制，凹腔处的涡流得到削弱，从而有效降低宽频噪声[25-29]；在缝翼凹腔及主翼前缘铺设声衬材料[20]，可保持原气动外形的情况下削弱缝翼噪声等。

C.C.Pagani等[21]及M.Herr等[22]通过实验及仿真手段分别研究了缝翼几何位置和结构变形对缝翼远场噪声的影响，其研究结果显示缝翼几何位置与结构变形均可在一定程度上减小缝翼噪声辐射，并能保持较高的气动性能。然而C.C.Pagani等及M.Herr等主要侧重实验研究，所采用的参数设置也比较有限，而且两者均较少涉及缝翼流场及其远场噪声特性的机理研究。

基于上述分析，本文通过对典型三段翼型的建模和仿真来研究缝翼流场特性以及缝翼噪声产生机理。着重研究调整缝翼几何位置参数和缝翼结构变形两种条件下缝翼流场特性以及缝翼噪声的产生机理，并对远场噪声的分布特性进行深入分析。

1 气动噪声数值计算方法

为有效求解缝翼远场噪声，本文采用LES(大涡模拟)方法计算三段翼瞬态流场，对三段翼的湍流情况进行数值模拟。并在此基础上通过求解Ffcows Williams-Hawings(FW-H)积分方程，获得三段翼的远场噪声。

LES在求解瞬态流场时，将湍流流动分为大尺度涡以及小尺度涡，其中大尺度涡起主导作用，而小尺度涡主要起耗散作用。将湍流中的大尺度涡同小尺度涡通过滤波分离，大尺度涡通过N-S方程求解，小尺度涡通过模型模拟。这种方法相比DNS方法大大减少计算工作量，同时提高湍流的模拟精度。

LES求解过程为：

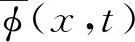
(1)

其中大尺度量为

(2)

式中：D为计算区域范围；G(x,x′)为确定涡尺度的滤波函数。

本文研究对象为不可压流体，采用滤波函数对不可压N-S方程滤波后，可得大涡模拟控制方程：

(3)

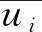
(4)

经过滤波后，控制方程中的亚格子应力项τij为未知项，需要通过构造亚格子模型得到。本文采用Smagorinsky-Lilly亚格子模型求解其亚格子应力。

2 数值计算与结果验证

2.1 缝翼模型及计算网格

本文采用30P-30N三段翼型，如图1所示。收紧弦长采用C=0.457 m，展开时基准翼型缝翼弦长占收紧弦长的15%，襟翼占收紧弦长的30%，两者偏角均为30°，缝翼参数如表1所示。

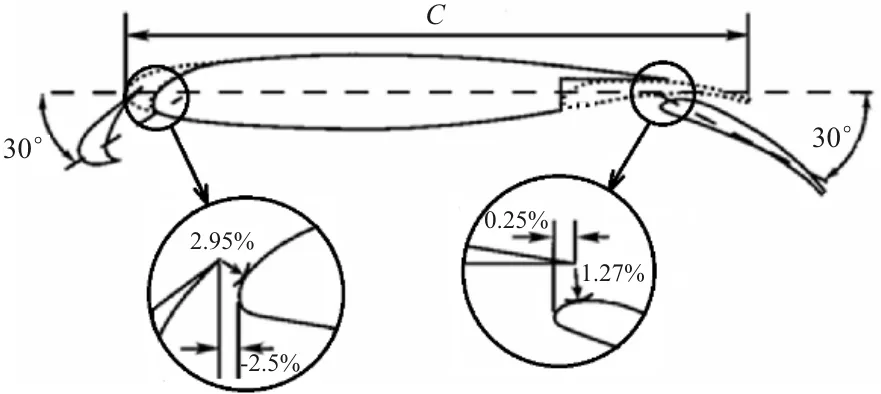
图1 翼型几何构型示例

Table 1 Slat paramenters 单位:%C

计算网格采用“C型”结构网格，计算域为25倍弦长，为了验证网格质量，本文采用一系列网格密度方式进行设计，结果发现在网格精度达到一定精度后，增加网格密度与质量对结果的改善非常有限，计算成本大大提高[29]。考虑到LES计算对网格的严格要求，最后选用网格总数约为33万，空腔处的网格数约为9.2万，占总网格数的1/4以上。第一层网格高度为1×10-5m，对应的Δy+≤1，边界层包含25个节点。其网格分布如图2所示。

(a) 增升装置附近网格

(b) 缝翼附近网格

2.2 流场与远场噪声的数值模拟

基于工况α=8°，Ma=0.17，收紧状态下弦长的雷诺数Re=1.7×106。具体数值模拟过程为：

①采用基于SSTk-ω湍流模型求解RANS方程，获得稳态流场，并计算升力系数；

②然后基于稳态流场结果，采用LES计算瞬态流场，为消除稳态解的影响，选择步长Δt=2×10-6s迭代6 000步，然后再迭代15 000步，获得瞬态流场数据；

③在求解远场噪声特性方面，参考Lockard等[26]文章，固壁积分面与可穿透积分面所得远场噪声特性基本一致，同时，当湍流流过可穿透积分面时，FW-H积分获得的解已不可信[27],由于本文主要关心的噪声频带范围为0～10 kHz,故本文选用缝翼固壁面为积分面，通过FW-H积分方程计算远场噪声分布；

④以收紧翼型前缘点为圆心，十倍弦长为半径，每隔5°计算远场辐射噪声级，以此获得噪声指向性图。

2.3 数值方法验证

基于上述分析方法进行数值计算，对30P-30N翼型的基准状态，并基于上述工况(α=8°,Ma=0.17)进行仿真，所得表面压力系数Cp与LAXA风洞[25]的实验值进行对比(如图3(a)所示)。可见，主翼前缘及压力面基本吻合，吸力面也基本相同。在缝翼后缘部分压力系数稍微有点不同。为进一步验证仿真的正确性，本文对工况α=8.12°，Ma=0.20进行仿真，并与NASA实验[24]进行对比，结果如图3(b)所示。仿真值与实验值基本吻合，充分验证仿真方法可行性。

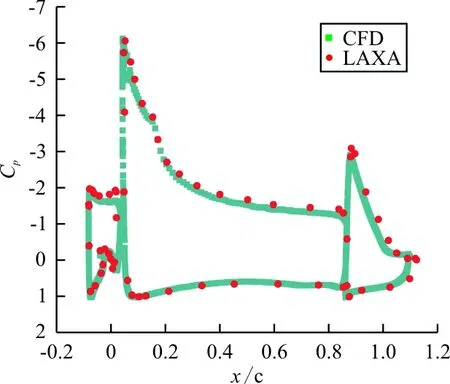
(a) Ma=0.17仿真值与LAXA风洞试验实验值对比

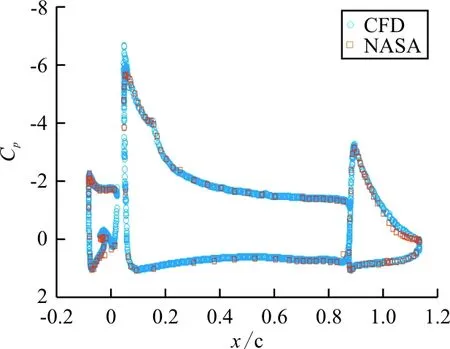
(b) Ma=0.20仿真值与NASA实验值对比

时均速度沿流线方向和垂直于流线方向的速度云图如图4和图5所示，仿真结果与LaRC实验值[21]吻合较好。

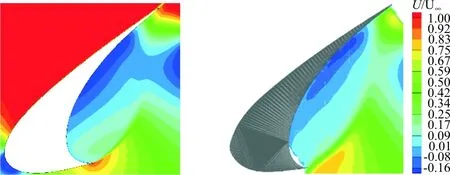
(a) 仿真 (b) LaRC实验

图4 沿流线方向的速度云图对比

Fig.4 Comparison of mean streamwise velocity

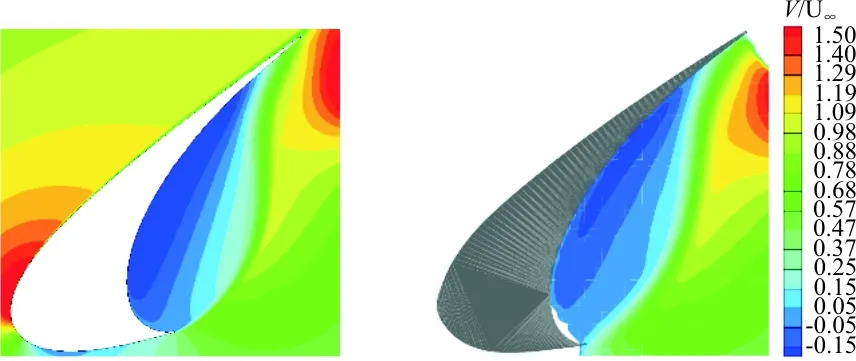
(a) 仿真 (b) LaRC实验

图5 垂直于流线方向的速度云图对比

Fig.5 Comparison of mean vertical velocity

从图4～图5可以看出：缝翼尖端处沿流线方向速度较大，而垂直于流线方向速度最大位置在主翼的前缘位置附近。

缝翼处气流时均涡量与实验值[23]对比如图6所示，剪切层形状与实验值基本一致，证明仿真较好地模拟出了缝翼空腔处涡的流动特性。

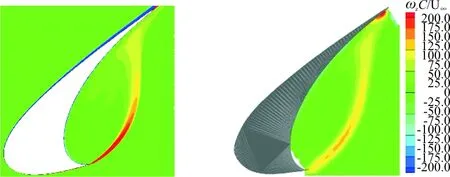
(a) 仿真 (b) LaRC实验

图6 时均涡量对比图

Fig.6 Comparison of time-averaged vorticity

湍动能(TKE)仿真值与实验值[23]对比如图7所示，可以看出二者在分布趋势上基本吻合，再附着位置与剪切层特征的趋势基本一致。

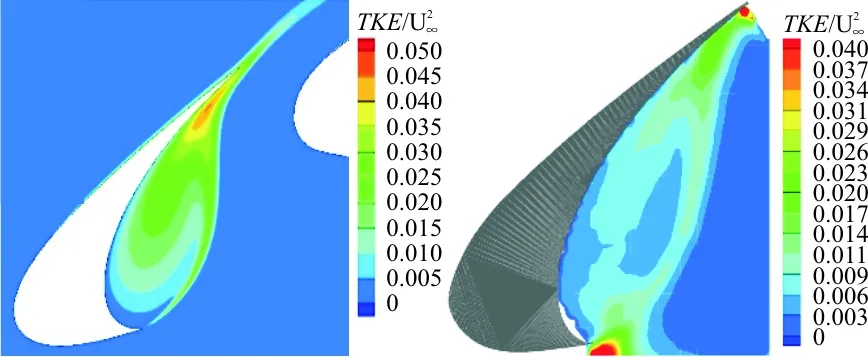
(a) 仿真 (b) LaRC实验

图7 湍动能云图对比

Fig.7 Comparsion of TKE

将原始位置下，监测点(0, -5c, 0)处，仿真所得远场噪声频谱与北航实验数据[30]对比，如图8所示。可看到本文2D仿真结果与北航实验数据吻合较好，由于采用了2D仿真，忽略了展向效应，导致低频噪声峰值仿真效果不理想。本文主要研究不同状态下的宽频噪声抑制情况，通过观察此监测点频谱图可知，二维情况下的噪声数值仿真具有合适精度，捕捉到缝翼噪声大致情况。

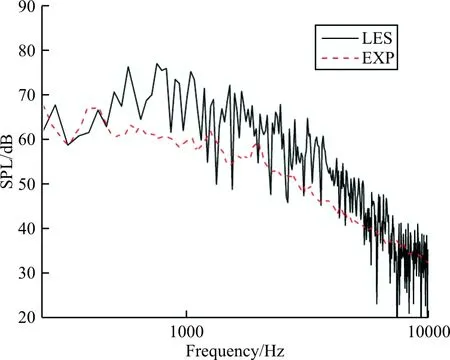
图8 远场噪声对比

3 缝翼几何参数与结构变形对噪声的影响

3.1 缝翼位移参数的影响

为了研究改变缝翼位移参数对翼型气动性能和噪声特性的影响，选择6组缝道宽度(Gap)和7组重叠强度(Overlap)进行组合，组合情况如表2所示。舍弃10个不合理组合后余下32个缝翼位移参数组合。以10C为半径，在翼型下方每隔25°取一个观测点(共7个点)计算远场噪声，最后以这7个点总声压级平均值(OASPL Average,简写为OASPLA)作为衡量噪声强度的依据。

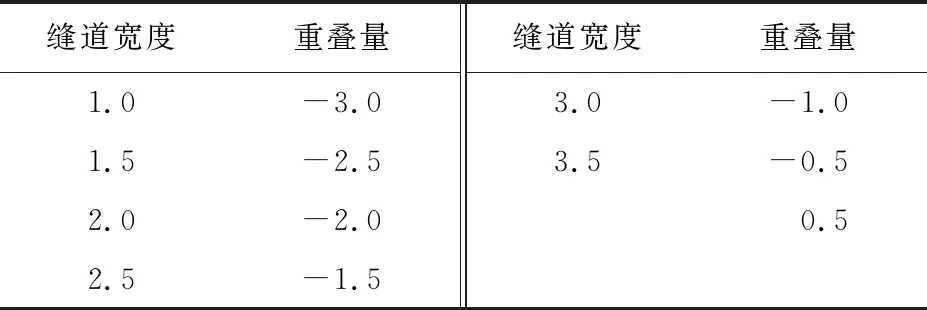
表2 参数设置

3.1.1 总声压及升力系数分析

针对上述32个缝翼位移组合参数，分别计算总声压平均值(OASPLA)与升力系数(CL)，并将结果以数据云图呈现，如图9～图10所示。基于图9选取3条典型线段作为缝翼位移参数变化的分析参数。L1代表噪声持续减小的变化线；L2为基于基准Overlap，只改变Gap的参数变化线；L3为具有较小噪声和较大升力的参数变化线。

分析发现：①当缝翼位移参数沿L1线段变化时，远场噪声变化较小，而CL变化较大；②重叠强度不变，只改变缝道宽度时(沿L2)，辐射噪声先降低再增大，而CL则持续减小；③缝道宽度不变，只改变重叠强度时(沿L3)，辐射噪声先降低再增大，而CL是先增大后减小，且Overlap在[-1.5,-1]区间变化时，噪声变化显著；④当Overlap为-0.5%C且Gap为1%C时，OASPLA最小，为86.6 dB, 比原位置减小了约8 dB(8.36%)，且CL较原始位置增大。

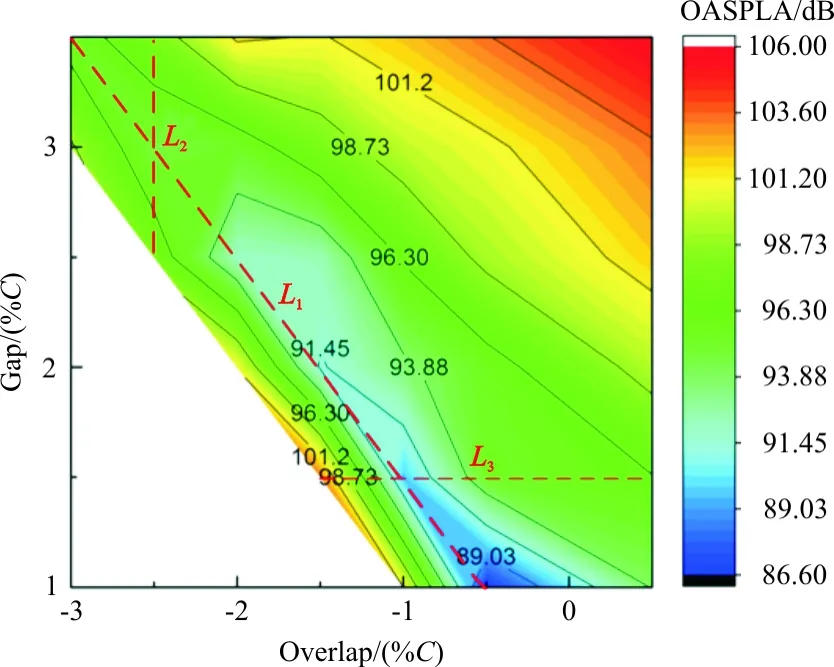
图9 OASPLA与缝翼位移参数的关系

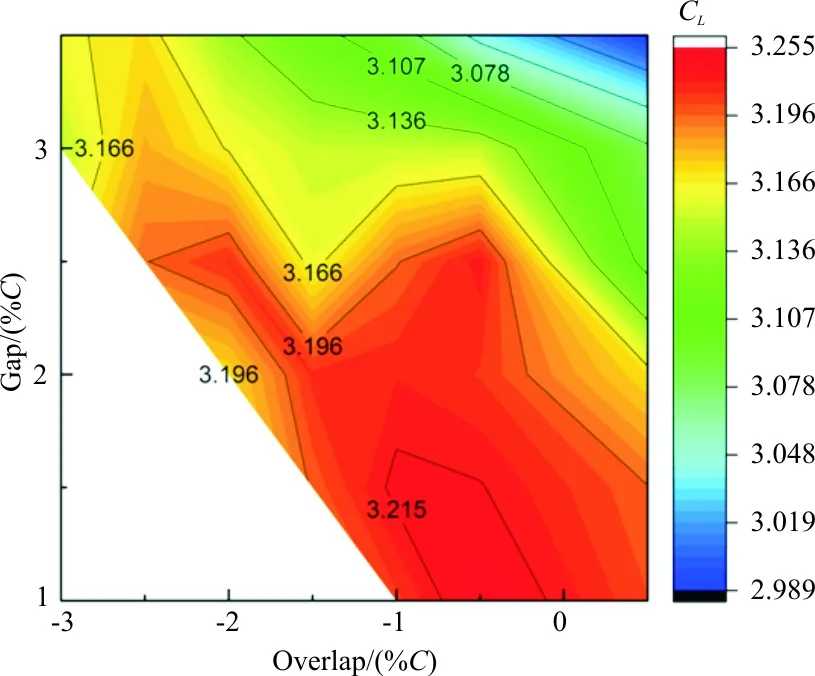
图10 CL与缝翼位移参数的关系

3.1.2 典型位置的湍动能分析

从数据云图中可见，缝道参数沿L1线段有明显的噪声降低特性，且具有较好的气动特性，故沿L1线段选择三个典型位移参数组合进行分析。为了便于说明缝翼位移参数调整相对于初始位置的变化，采用位置命名法，例如：O-2.5G2.95，指代翼型30N-30P的原始位置，即Overlap为-2.5%C，Gap为2.95%C。以下进行湍动能分析：位移参数分别为O-2.5G2.95,O-1.5G2.0,O-0.5G1.0的TKE云图如图11所示。当Gap减小，Overlap增大时，缝翼压力面尾缘处附近(再附着位置)TKE强度逐渐减弱。M.M.Choudhari等[11]和J.Tao等[12]认为缝翼宽频噪声是由剪切层涡流与缝翼尾缘压力面剧烈碰撞(再附着位置)，形成大量离散涡，从而产生较强宽频噪声。对比图8和图11发现：缝翼远场噪声与缝翼再附着位置处的TKE强度有着密切联系，较大的TKE强度是引发宽频噪声的重要因素。

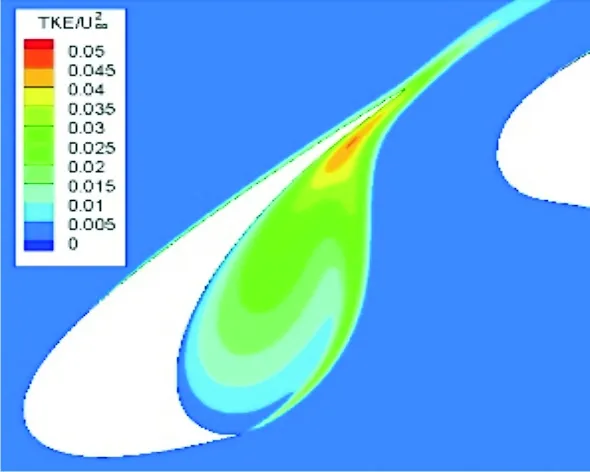
(a) O-2.5G2.95

(b) O-1.5G2.0

(c) O-0.5G1.0

3.1.3 典型位置频率特性分析

沿L1线段上取五个缝翼位移参数组合，取翼型收紧状态前缘点垂直向下10C处为观测点，其1/3倍频谱图如图12所示。在低于6 kHz范围内，Gap减小且Overlap增大时，有利于噪声的减小。位置组合O-0.5G1.0在1 kHz附近降噪尤为明显。

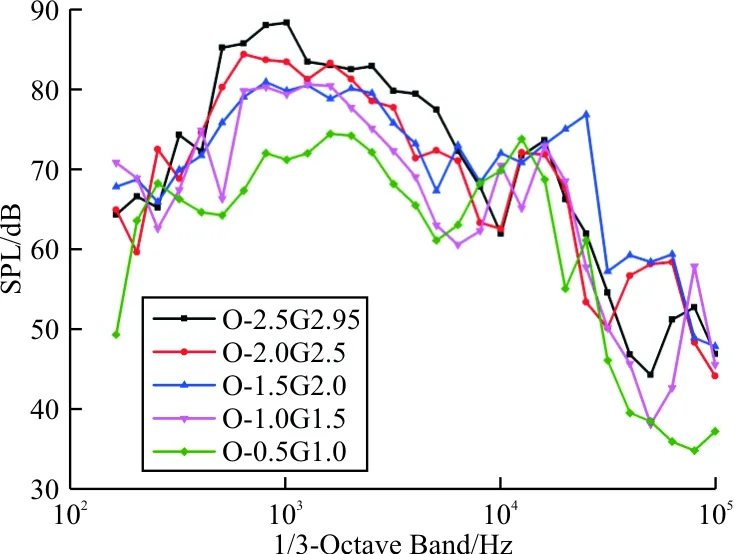
图12 1/3倍频谱图

3.1.4 典型位置OASPL指向性图

沿L1线，取O-2.5G2.95，O-2G2.5，O-1.5G2，O-1G1.5，O-0.5G1.0五个位置，绘制其远场噪声指向性图，如图13所示。

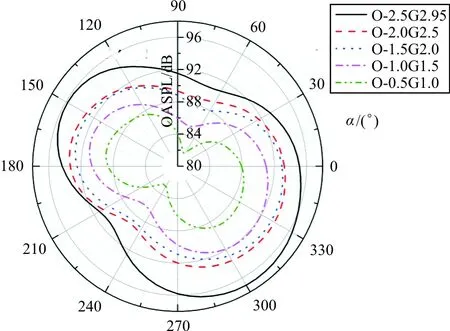
图13 OASPL指向性图

从图13可以看出：缝翼噪声是一个典型的偶极子声源；随着Gap减小和Overlap增大，噪声强度不断减弱；峰值出现在315°附近，该方向与缝翼弦向基本垂直。

3.2 缝翼偏转角的影响

缝翼偏转角δ也是重要的位置参数。以O-0.5G1.0为基准，缝翼尾缘尖端为轴心，顺时针偏转为正。取δ范围为-6°～10°，间隔为2°。缝翼噪声OASPLA和CL随δ的变化情况如图14所示。

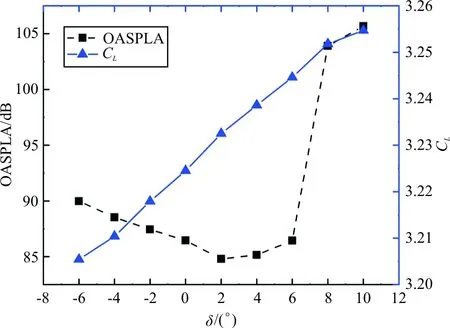
图14 OASPLA和CL随δ的变化

从图14可以看出：CL随着δ增加基本呈线性增大，而OASPLA则先减小后增大，特别是当δ超过6°后，OASPLA迅速增大。因此小幅增加δ(≤6°)有助于降低OASPLA的强度。

3.2.1 0°偏角与8°偏角湍动能对比

δ为0°和8°时的TKE云图如15所示。

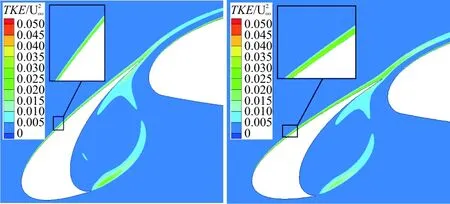
(a) 0°偏角 (b) 8°偏角

图15 TKE云图

Fig.15 TKE cloud pictures

从图15可以看出：δ=8°时，缝翼空腔处的湍动能相对于0°时有略微的减小，但其缝翼上表面出现了较强的湍流，这可能使得该处的噪声强度变大。

3.2.2 典型偏角位置频率特性分析

典型δ的1/3倍频谱图如图16所示，可以看出：δ过大(δ=8°)时，在频率为0.5～10 kHz区域内噪声明显较大；δ为-4°和4°，在0.5～1 kHz区域比0°时噪声大，但在0.25 kHz附近及4～10 kHz处，4°时噪声较小；-4°时，在0.3～1.2 kHz区域宽频噪声及12.5 kHz附近的窄带高频噪声较强。

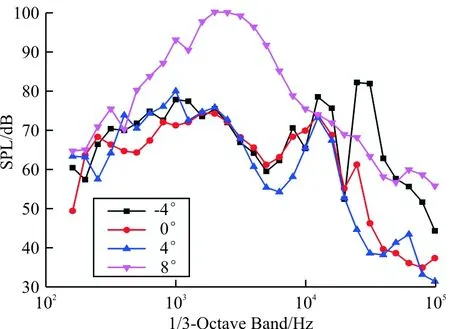
图16 典型δ的1/3倍频谱图

3.2.3 典型偏转角的OASPL指向性图

δ从-4°～8°的OASPL指向性图如图17所示，可以看出：δ较小时的噪声指向性图形状基本一致；δ=8°时，其指向性图发生显著的变化，辐射噪声在各个方向上均较大。

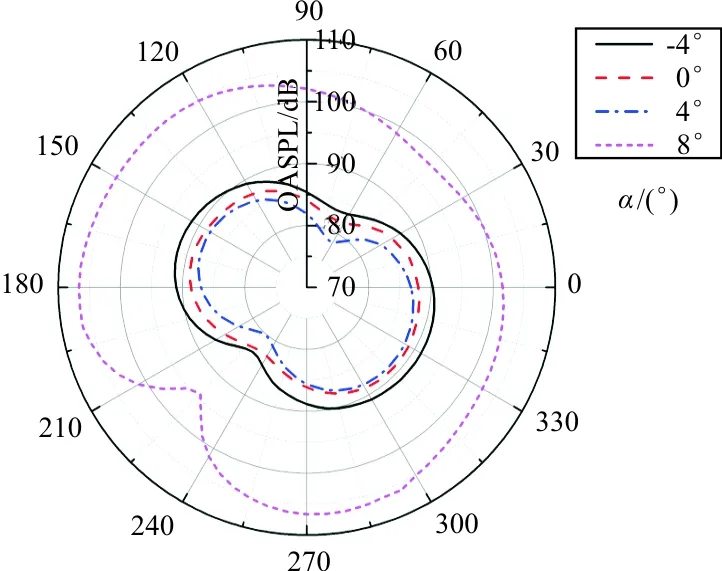
图17 典型δ的OASPL指向性图

3.3 缝翼变形的影响

若通过缝翼自适应变形(利用作动筒将缝翼后缘变形)，将缝道完全封闭，凹腔处的剪切层噪声源以及由剪切层碰撞带来的再附着位置的宽频噪声源将完全消除。因此，本文考虑缝翼结构变形，使缝翼尾缘向下偏转封闭缝道，如图18所示。本文共设计三个典型变形状态：S1(O-1.72G2.5位置下变形)，S2(O-0.29G2.78位置下变形)和S3(O-0.24G1.32位置下变形),以及基准位置S0(O-2.5G2.95)。

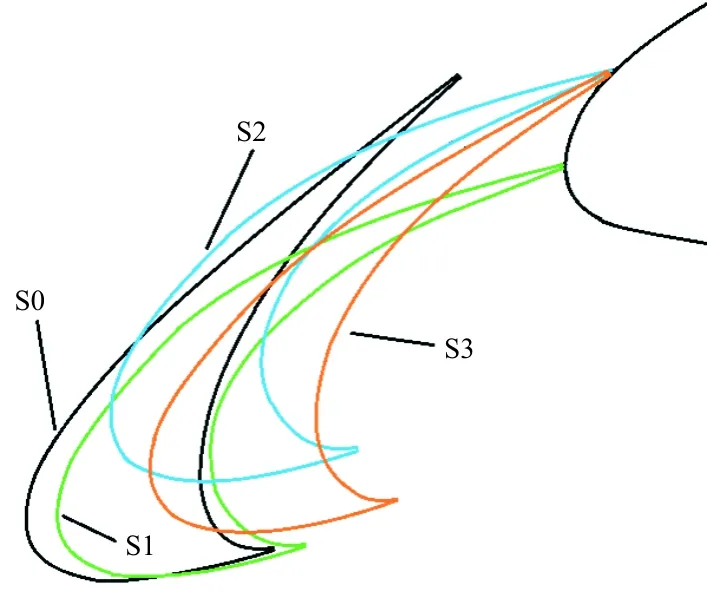
图18 变形前后位置

四种状态下的CL和OASPLA如表3所示，可以看出：封闭缝道可极大地减小缝翼远场噪声辐射，特别是在S3状态下对OASPLA的削弱量达到11.6 dB；同时S1翼型的CL比S0大，S2和S3的CL则略有减小。

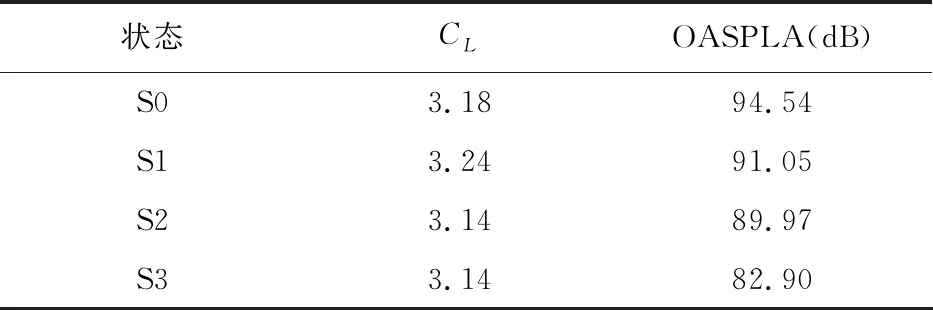
表3 不同变形下CL和OASPLA

3.3.1 不同变形的TKE分析

变形前后的TKE云图如图19所示。可以看出：①封闭缝道后，缝翼凹腔处的TKE明显减小；②当缝翼为S1状态时，由于缝翼与主翼过渡不连续，在封闭位置上端部分附近出现很强的TKE；③当上移封闭位置到S2状态，缝翼与主翼的过渡变得连续，封闭位置上端部分的TKE显著减弱，但吸力面(即框体标识部分)TKE强度增大；④当缝翼为S3状态时，缝翼与主翼的过渡更加连续，同时由于变形量较小，这使得其在封闭位置附近的TKE进一步降低，吸力面(即框体标识部分)有较大TKE。

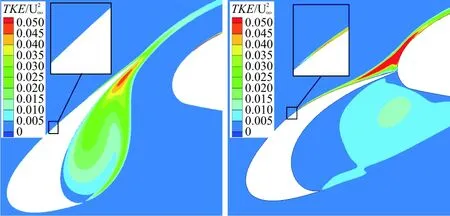
(a) S0状态 (b) S1状态

(c) S2状态 (d) S3状态

图19 变形前后TKE云图

Fig.19 TKE for morphed and original slat

3.3.2 不同变形的频率特性分析

不同变形的1/3倍频谱图如图20所示，可以看出：变形封闭缝道后，在0.23 kHz及0.5～2 kHz的中频噪声相对于基准位置均有减小，但在2 kHz之后，S1，S2噪声相比S0增大，可能是缝翼吸力面以及与主翼相接部分出现较强湍流所致。S3由于封闭位置过渡连续，使其在吸力面的湍流强度得到抑制，从而在频率范围内降噪效果显著。

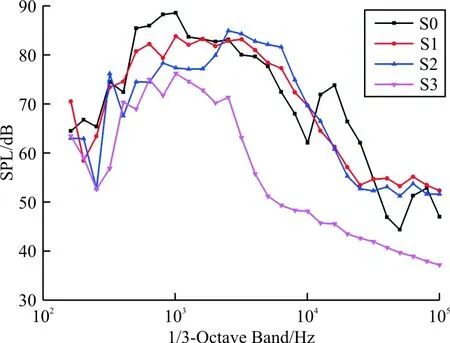
图20 不同变形的1/3倍频谱图

3.3.3 变形前后OASPL指向性图

不同变形的OASPL指向性图如图21所示，可以看出：缝道封闭极大地改变了远场噪声的方向性。除S1在235°和S2在60°～110°噪声比基准位置S0大以外，S1、S2和S3的噪声在各方向上均有所减小。S3由于在消除原有噪声源的基础上几乎没有引入新的噪声源，因此其噪声相对于S0显著减小。

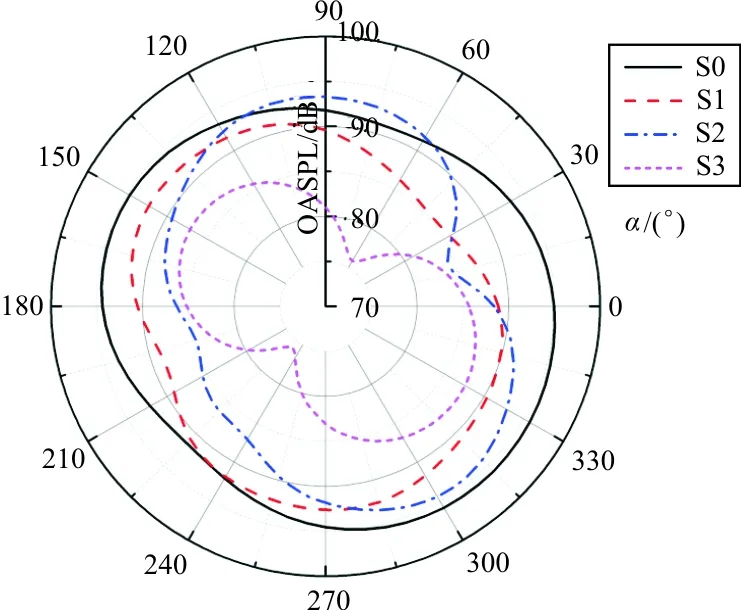
图21 不同变形的OASPL指向性图

4 缝翼参数调整与失速特性分析

基于以上缝翼几何参数与变形对噪声影响的研究，本文选择三种降噪较优的方案：O-0.5G1.0，O-0.5G1.0(4°)(即δ=4°)和S3，对其升力线特性进行研究，如图22所示。可以看出：上述方案的升力线斜率基本不变，而最大升力系数均有所减小，特别是缝道封闭的S3状态，在大攻角下升力下降显著，失速迎角也较小。基于O-0.5G1.0位置向上偏转缝翼，即O-0.5G1.0(4°)，最大升力系数会有所减小。

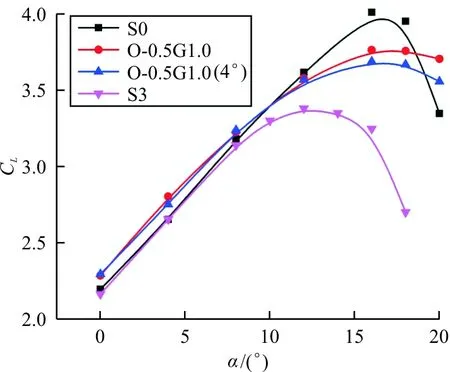
图22 不同缝翼参数下CL随迎角α的变化曲线

5 结 论

(1) 调整缝翼位移参数，可显著减小缝翼宽频噪声，同时保持较大升力。例如在O-0.5G1.0位置，可削弱OASPLA近8.36%。

(2) 基于本文翼型，增大缝翼偏转角δ，可减小远场噪声辐射，但当δ增大到一定值(本文为6°)，缝翼噪声将急剧增大。

(3) 缝翼自适应变形封闭缝道可消除剪切层涡流与压力面的碰撞，减小宽频噪声(S3最大可降低约11.6%)。但封闭的缝翼尾缘应与主翼平滑过渡，这样可避免引入新的噪声源。

(4) 本文所选状态参数下，最大升力系数有一定程度上的减小，尤其是变形封闭缝道的情形，在采用自适应变形缝翼降噪时，需考虑飞行迎角的适用范围。