3D软件入课堂,空间直观提素养
廖小琴 邵贵明

【摘要】《普通高中数学课程标准(2017年版)》提出直观想象是高中数学学科核心素养之一,是学生通过学科学习而逐步形成的正确价值观念、必备品格和关键能力.本文提出使用3D软件辅助教学可以展示空间图形,为学生理解和掌握图形几何结构与特征提供直观.通过例子阐述3D软件在数学课堂中的作用,并探讨了在此技术的辅助下如何引导学生提升几何直观数学素养.
【关键词】3D软件;直观想象;数学核心素养
普通高中数学学科核心素养的六大核心素养——数学抽象、逻辑推理、数学建模、直观想象、数学运算、数学分析中,直观想象是高中学生必须具有的数学核心素养之一.要求学生会借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题.主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律利用图形描述、分析数学问题;建立形与数的联系,构建数学问題的直观模型,探索解决问題的思路.[1]高中立体几何的学习主要在培养空间抽象能力的基础上,发展学生的几何直观能力和空间想象能力.立体几何是中学数学的一个难点,学生普遍反映“几何比代数难学”.其原因就是学生缺乏直观想象力.而高一年级是立体几何学习的起始年级.学生在初中阶段接触的是一些简单的平面几何内容,他们在这一阶段并没有建立起比较强的空间感,所以学起来就更加吃力.
而时下中国信息技术已经进入了3D时代.3D建模技术和3D打印技术实现了用“虚拟”再造“现实”的崭新境界.3D制作当然也离不开考验制作者的直观想象力和几何计算能力.例如,要3D打印一个螺栓和螺帽,那么螺栓圓柱体底面圆的直径要设计多大才能对应到螺帽呢?大了则套不进,小了则会松.所以,在3D打印中,立体几何的直观想象变得尤为重要.故此,作为高中数学教学工作者,我们有责任培养出具有直观想象素养的人才,为学生以后的发展做好能力铺垫.同时,反过来3D软件也可以为我们的教学服务,让立体几何教学更具有生动性、直观性,有利于学生认清空间事物的位置关系、形态变化与运动规律;利用3D图形动态描述、分析解决数学问题,提升几何直观数学素养.下面以例子展开本人在3D软件辅助教学的一些体会.
一、巧用软件认清空间事物的位置关系、形态变化与运动规律
与球组合的几何体问题,一种是内切、一种是外接,这两种特殊的位置关系在高考中既是必考题型,又是难点,但学生往往因缺乏空间想象能力而感到模糊.在“正方体的内切球和外接球”这节课上,内切球和外接球的理解和作图是一个难点.如果我们不做任何的展示,而直接让学生生成直观图时,会出现有一些学生把多种球之间的关系搞混乱:内切球画成了内含球,外接球画成外包球.然而,在传统教学中,我们很难找到现成的教具展示给学生看,到底“切”是怎么切的,而“接”又是怎么个接法.教学上非常需要一个教具让学生从不同的视觉角度观察球内切或外接正方体时正方体的点、线、面与球的球心和半径等要素之间的关系.
如果这个时候,教师及时采用3D软件把球从内含到外包的过程进行动态演示,并在过程中点出内切球的“切”是跟正方体的面的中心相切,而外接球的“接”是跟正方体的各顶点相接.演示过程中就能非常清晰地把球与正方体之间的位置关系形象地展现给学生,而这些动态展示又恰恰是传统教学或实物展示所不能比拟的!
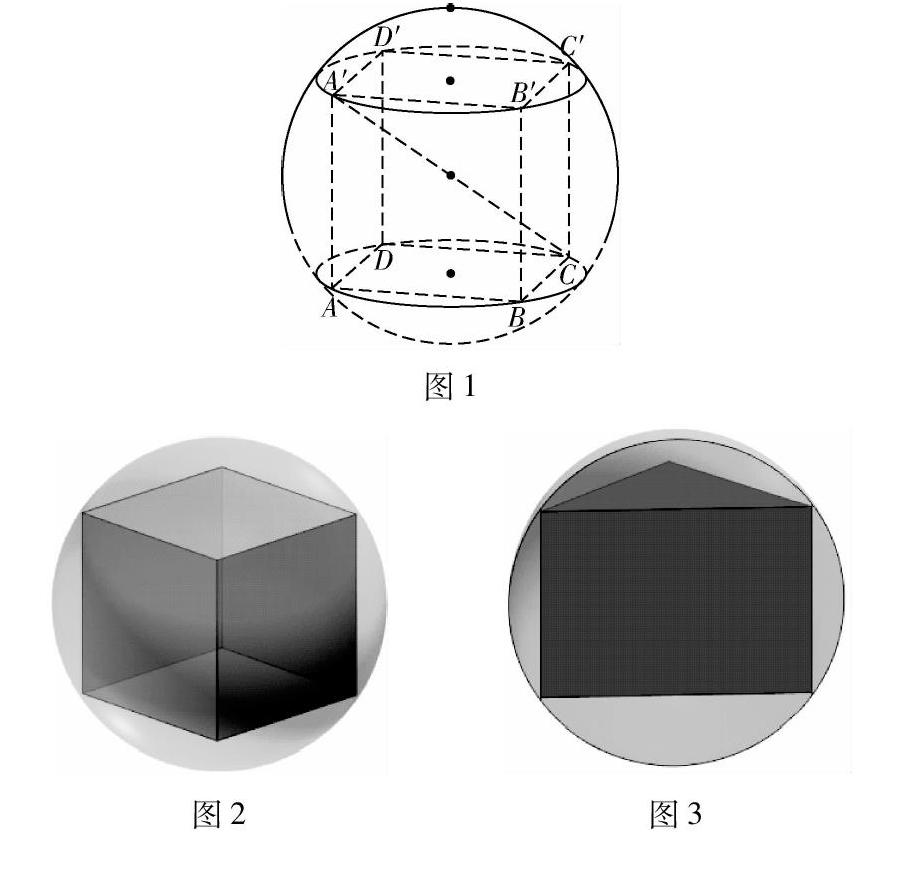
同时,在这节课上学生对外接球直径是正方体体对角线的理解也是一个难点.怎样才能体现正方体的体对角线就是外接球的直径呢?传统教学中很难用语言清晰地描述给学生听.即使采用作图法给出了图1,把正方体画成内接在小圆和大圆搭建的球框架内,也会存在有学生因缺乏空间想象力看不懂直观图而无法理解的情况.在传统教学上我们是通过正方体外接球对角面的截面图展现给学生,学生通过想象还原到正方体当中理解.但为什么要画对角面的截面图呢?传统教学上也是比较难直观地告诉学生.但运用3D软件对实物进行360度的旋转展示,就可以直观地找到如图2所示的视角,非常清晰地展现正方体对角面上的所有点都在球面上,而球心也在面内的对角线上.通过软件还能进一步地在直观图上切割出正方体外接球的对角面(如图3所示),使得学生获得更直观的体验.
著名数学教育家波利亚说:“数学有两个侧面:一方面,是欧几里得式的严谨科学,从这方面看,数学像是一门系统的演绎科学;但另一方面,创造过程中的数学,看起来却像一门实验性的归纳科学.”这节课还可以更有趣的是:再给出一些非正方体的几何体,让学生自己尝试利用3D软件作出其内切球或外接球并通过观察研究出其半径.通过3D软件进入课堂,我们可以将抽象的问题具体化,有效地为学生提供感性材料,化静为动,具有图文并茂、形象直观、动态逼真等特点.它能充分展示立体知识的形成和思维过程,促使学生“知其然并知其所以然”.
二、利用3D图形动态描述、分析、解决数学问题,提升几何直观数学素养
3D软件辅助教学独特的价值,在于通过整合为学生提供逼近真实、富有现实意义的学习情境,以利于学生高阶思维与积极情感的投入,解决复杂问题,从而全面提升学生知识、能力与情意方面的核心素养.[3]其实,在解决空间几何问题时,在直观图中许多原本相等、平行、垂直或异面的直线由于“变形”“倾斜”等原因,学生很难观察出来,而导致问题解决错误或解决不了.但当几何体经过“3D转动”后,或许就能把原本难以理解或想象的问题变得更直观和简单,同时也能更快地培养和锻炼学生的“立体平面图的空间感”,迅速提升直观想象素养.
在这道题中,对刚接触立体几何的高一学生来说,由于缺乏空间感,有些学生就会把AC1与BC理解为相交直线来求,结果就会出现问题.但如果我们在课堂中尝试使用3D软件从不同角度展现该长方体,当出现如图5所示的视角时就能让学生看出AC1与BC这两条直线是异面直线,不相交的关系,从而引导学生通过找平行线的方法找出∠AC1B1就是AC1与BC所成的角的平面角.
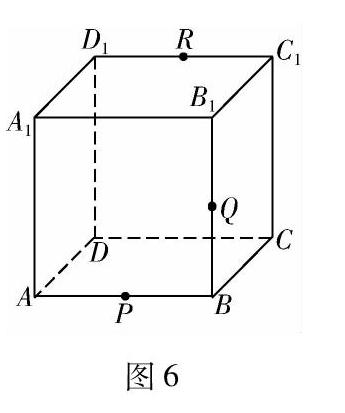
题意是让学生画出PQR平面截取正方体后的形状,也就需要学生把该截面与正方体的其余相交直线画出来.这道题是对学生的空间思维能力提出了更高的要求.很多学生都不能完成.故此,我们可以尝试使用3D软件辅助解题.首先,我们可以在3D软件中建立正方体.
然后,旋转角度连接PQ,并延长PQ,使其与A1B1相交于E点.
再连接RE交B1C1于F点.
此时,不难证出△PQB≌△QB1E≌△B1EF≌△RC1F,所以点F是B1C1中点.而此时相交直线RF与PQ所确定的平面就是我们要找的截面.
如此类推,我们把正方体像骰子般转动,由此而引导学生继续思考探究.问是否能作出該截面在其他平面上的交线呢?通过引导让学生把该截面在正方体其余各面的交线画出来.最后我们再利用3D软件中的切割工具对几何体进行切割,很快就可以得出切面.
同时,再把切割平面转正,由此而检验学生作出的平面是否与软件作出的平面一致,并能直观地看出所截取的平面就是正六边形.
一幅幅的3D动态画面在展示和推导中能不断地带动学生深入分析问题,使学生在不断的观察和分析中形成直观想象素养.深度教学领军人郭元祥教授曾提出:增强课堂的画面感是促进学生知识理解,获得知识的意义增值,达成知识发展价值的基本途径.课堂的画面感通过将知识表征化促进学生对符号知识的深度理解.[4]3D软件参与解题的过程才能引起学生丰富多样的再造想象、创造想象和以后在解题过程中就会自然而然产生的空间几何联想.
直观想象是解决立体几何问题的重要核心素养.通过3D软件对几何体的翻转变换、伸缩变形、切割变化等操作过程有利于提升学生对几何体的直观理解和形成空间想象,降低数学解题的门槛,使得复杂问题直观化.同时,也会促使学生在以后解题中能自动生成换位思想和几何联想,直观想象素养自然而然得到提升.总之,要提升学生发展的核心素养,需要师生每一堂课的积累与努力.教师本身要勇于学习研究3D软件、积极实践,开展学科课堂教学改革,才能有效落实和提升学生核心素养的培养.
【参考文献】
[1]中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2017.
[2]林静.STEAM教育如何对接核心素养[J].师资建设,2017(30):51.
[3]秦德生,孔凡哲.关于几何直观的思考[J].中学数学教学参考,2005(10):9-11.
[4]郭元祥.增强课堂的画面感——谈课程改革的深化(5)[J].新教师,2016(5):13-15.

