中国股票市场指数波动特征研究

摘 要:价格波动性是资本市场微观结构特征中的重要特性之一,本文以GARCH模型理论为基础,选取具有代表性的上证综指作为股票指数研究对象,建立GARCH模型族,探究我国股票市场的波动特征。研究表明我国股票指数日收益率具有波动聚集性、持久性及“尖峰厚尾”等分布特征。同时,发现风险溢价理论在我国市场并不适用。此外,我国股票指数具有非对称特征,表现出明显的杠杆效应。最后本文结合实证分析,从监管者与投资者角度提出相应建议。
关键词:股票指数;波动特征;GARCH模型;价格行为
2018年11月5日,国家主席习近平出席首届中国国际进口博览会开幕式并发表主旨演讲,宣布在上海证券交易所设立科创板并试点注册制。2019年3月18日,科创板发审系统正式上线,中国股市迎来“科创板时期”。科创板独立于现有主板市场,对于中国股市还是新事物。通过研究我国现有主板市场波动特征可以刻画出资产价格行为,更好地实现价格发现过程,这对于科创板稳定运行、健康发展具有一定借鉴意义。
一、波动理论模型
传统的计量经济学对时间序列变量的第二个假设为时间序列变量的波动幅度即方差是固定的。随着经济模型的发展及实证研究的深入展开,研究学者发现这一假定与实际相差较大。对于股票而言,其收益的波动幅度就是随时间而变化的,并非常数。这使得传统的时间序列分析对实际问题并不有效。Engle(1982)在研究英国通货膨胀率的波动性时首次提出了ARCH模型,解决了时间序列的波动性问题,为今后的研究奠定了基础。
(一)GARCH模型
ARCH模型运用于实际情况时,误差项的条件方差会依赖于多期之前的变化量,参数较多的情况存在较难精确估计的缺陷。针对该问题,Bollerslev(1986)提出了广义自回归条件异方差模型——GARCH模型,即用较为简单的低阶GARCH模型代替高阶ARCH模型,降低参数估计的复杂性。GARCH模型可表示为式(1-1)(1-2)与(1-3):
(1-3)
(二)GARCH-M模型
基于投资组合理论,学者考虑到资产价格的波动可能会对收益产生影响。Engle、Lilien和Robins(1987)提出了均值自回归条件异方差模型——ARCH-M模型,在均值方程中引入误差项的条件方差或标准差,如式(1-4)所示:
(三)EGARCH模型
上述模型中,误差项的条件方差是过去误差项平方的函数,且各项系数均要求为正数,误差项的符号并不影响波动情况,即收益率正向或负向变化,波动的反应都是对称的。然而,在实践过程中发现,资产价格对于正负冲击表现出不同的波动大小,通常将这种非对称现象称作“杠杆效应”。
EGARCH模型,即指数广义自回归条件方差模型,即是为了表现市场中存在的“杠杆效应”。该模型的条件方差方程如式(1-5)所示:
二、实证研究
本文的研究对象为上证综指,选取样本区间从2015.1.9至2018.12.28,共计971个交易日的日收盘价数据,进而分析日收益率序列统计特征,并建立GARCH模型族来探究我国股票市场指数的波动特征。
(一)日收益率序列特征
由于篇幅所限,在此不对图表进行展示,仅做出总结。研究发现日收益率分布呈左偏态,且分布的下尾部比上尾部密集,峰度值大于正态分布的峰度值3,说明其分布的尾部比正态分布厚。因而,上证综指日收益率分布并不是正态分布,而是表现出“尖峰厚尾”的特征。此外,上证综指日收益率时序列较为平稳,通过了单位根检验,并做了自相关检验进一步验证结论。同时,收益率序列的波动表现出聚集现象。
(二)日收益率序列建立模型
本文首先对上证综指的日收益率序列建立了ARCH模型的均值方程,表明其存在自回归条件异方差性,且存在高阶ARCH效应,因此考虑建立GARCH模型族,刻画股票指数收益率的波动特征。
1.GARCH模型
建立GARCH(1,1)、GARCH(1,2)、GARCH(2,1)、GARCH(2,2)模型来确定合适的滞后阶数,通过比较系数的显著性等条件,表明GARCH(1,1)模型对数据的拟合效果比较好。模型拟合参数结果如表1所示:
相对于OLS估计的方程结果(篇幅所限未列出),该模型的可绝系数、AIC等各个指标都有所改进,说明GARCH(1,1)模型拟合的较为合理。其次,本文对拟合方程进行ARCH-LM检验,结果如表2所示。由其可知,残差序列的置信概率均大于显著性水平,因此接受序列不存在自回归条件异方差的原假设,说明GARCH(1,1)模型很好地消除了日收益率殘差序列的异方差成分。
2.GARCH-M模型
均值方程P! 7上,黄凝——中国股票市场指数波动特征项系数为正值但不显著的结果表明股票指数波动率增大并不会对收益率产生较为显著的影响,说明投资者持有高风险资产不一定能获得相应的收益补偿,市场上或许存在大量非理性的投机行为。
3.EGARCH模型
接下来,本文对上证综指日收益率建立EGARCH模型,分析市场对于非对称冲击的反应。条件方差方程估计的参数如表3所示。
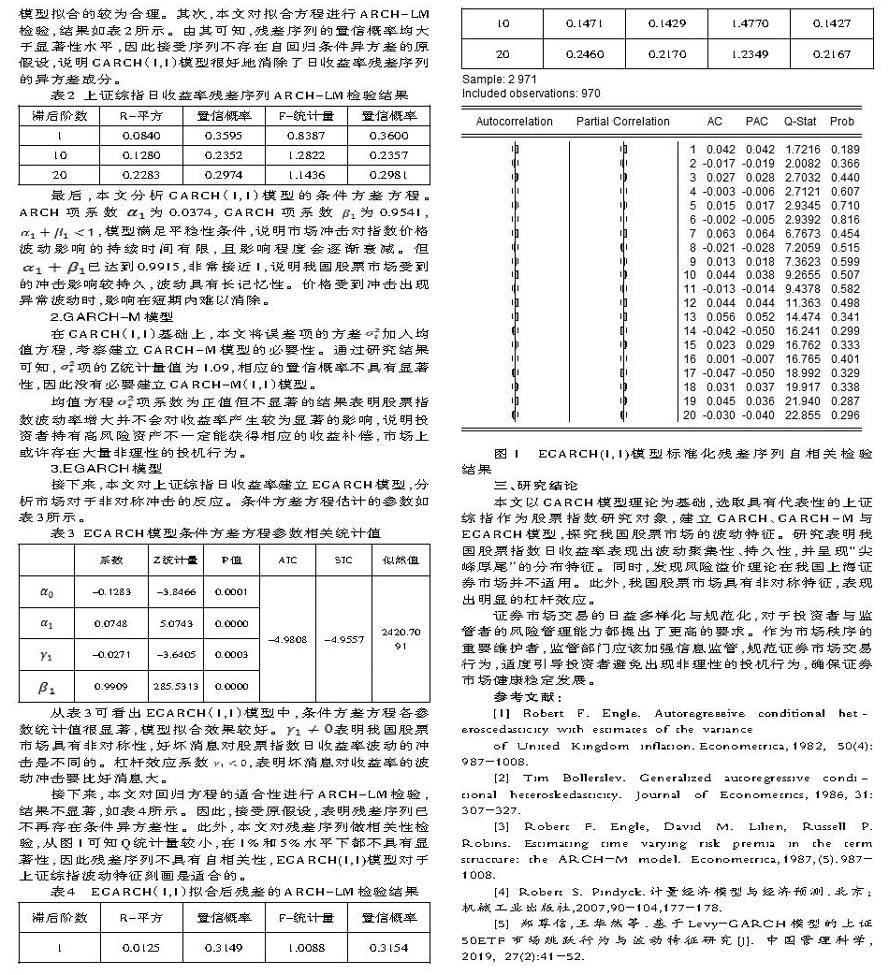
接下来,本文对回归方程的适合性进行ARCH-LM检验,结果不显著,如表4所示。因此,接受原假设,表明残差序列已不再存在条件异方差性。此外,本文对残差序列做相关性检验,从图1可知Q统计量较小,在1%和5%水平下都不具有显著性,因此残差序列不具有自相关性,EGARCH(1,1)模型对于上证综指波动特征刻画是适合的。
三、研究结论
本文以GARCH模型理论为基础,选取具有代表性的上证综指作为股票指数研究对象,建立GARCH、GARCH-M与EGARCH模型,探究我国股票市场的波动特征。研究表明我国股票指数日收益率表现出波动聚集性、持久性,并呈现“尖峰厚尾”的分布特征。同时,发现风险溢价理论在我国上海证券市场并不适用。此外,我国股票市场具有非对称特征,表现出明显的杠杆效应。
证券市场交易的日益多样化与规范化,对于投资者与监管者的风险管理能力都提出了更高的要求。作为市场秩序的重要维护者,监管部门应该加强信息监管,规范证券市场交易行为,适度引导投资者避免出现非理性的投机行为,确保证券市场健康稳定发展。
参考文献:
[1] Robert F. Engle. Autoregressive conditional heteroscedasticity with estimates of the variance
of United Kingdom inflation.Econometrica,1982, 50(4):987-1008.
[2] Tim Bollerslev. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics,1986,31:307-327.
[3] Robert F. Engle, David M. Lilien, Russell P. Robins. Estimating time varying risk premia in the term structure: the ARCH-M model. Econometrica,1987,(5).987-1008.
[4] Robert S. Pindyck.计量经济模型与经济预测.北京:机械工业出版社,2007,90-104,177-178.
[5] 郑尊信,王华然等.基于Levy-GARCH模型的上证50ETF市场跳跃行为与波动特征研究[J]. 中国管理科学, 2019, 27(2):41-52.

