例谈纸片在初中数学实验中的教育功能
魏玉华
(江苏省苏州高新区实验初级中学)
数学实验是学生运用有关工具(如纸片、剪刀、模型、测量工具、作图工具,以及计算机等),在数学思维活动的参与下进行的验证或探究活动.近年来,数学实验在初中数学教学和教研中蓬勃发展,从理论探寻到实践研究,从实验设计到工具开发,数学实验正悄然改变着初中数学教与学的方式.在众多的实验工具中,纸片以其易观察、可移动、成本低、易操作等优点,被广泛应用于数学实验教学中,并在不同层面发挥着诸多教育功能.
一、从知识理解看:促进知识的意义建构
数学概念和定理是数学知识体系的基本单位,让学生正确理解、掌握和运用数学概念和定理是教学中一项非常重要的任务.数学概念和定理的教学,通常包含三个环节:概念(定理)的引入、概念(定理)的讲解、概念(定理)的运用和巩固.这三个环节是一个循序渐进、环环相扣的有机整体,缺一不可.在实际教学中,常有忽视前两个环节,将概念、定理课上成习题课的情况发生,从学生的认知发展规律来看,不利于学生对概念和定理的理解,也不利于学生能力和素养的提升.某些概念和定理具有一定的抽象性,倘若借助数学实验,选取适当的教学工具,在“做”中实现概念、定理的意义建构,这对概念、定理的学习是非常有意义的.
案例1:图形的旋转.
活动1:操作与观察.
(1)将透明纸覆盖在图1中的△ABC上,描出△ABC,用大头针在点C处将透明纸片固定,再将透明纸片上的△ABC逆时针旋转一定的角度,得到△DEC.∠ACD和∠BCE有怎样的数量关系?改变旋转的角度和方向,结论依然成立吗?

图1
(2)将透明纸片分别覆盖在图2、图3的△ABC上,描出△ABC,用大头针在点O处将透明纸片固定,再将透明纸片上的△ABC旋转到△DEF的位置,说出旋转方向和旋转角度.

图2

图3
(3)图形旋转前后,其形状和大小有怎样的变化?
活动2:操作与思考.
(1)将透明纸覆盖在图4的△ABC上,描出△ABC,用大头针在点O处将透明纸片固定,再将透明纸片上的△ABC顺时针旋转一定的角度,得到△DEF.连接点O与三角形各顶点,图中有哪些相等的线段和相等的角?改变旋转的角度和方向,结论依然成立吗?

图4
(2)图5和图6中的△ABC经过旋转可以与△DEF重合.试确定图4和图5的旋转中心O,并借助透明纸进行验证.说说你是怎样确定旋转中心的?

图5
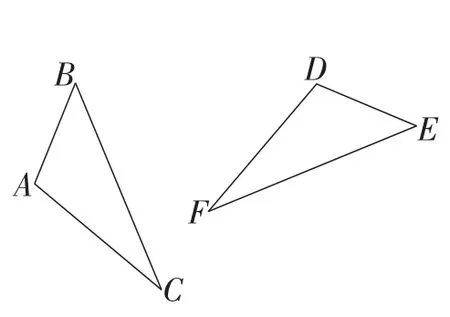
图6
活动3:思考与画图.
(1)在网格纸中画出△ABC绕点O顺时针旋转90°,180°,270°后的图形;
(2)画出将四边形ABCD绕点O按逆时针方向旋转120°所得到的四边形.
通过对摩天轮、钟摆旋转的观察引入课题,此时对旋转概念的理解是初步的,对旋转三个要素的认识还不够清晰.通过“操作与观察”环节(1)中的操作活动,借助透明纸的可覆盖、可移动、易观察的特点,使旋转不仅可视化,而且可操作化,在动手实践中感受旋转是图形绕一个定点转动一定角度的图形运动,体会旋转中心、旋转方向、旋转角在旋转运动中的作用.通过环节(2)及时巩固旋转的概念及三要素.在环节(1)(2)的基础上获得旋转的第一个性质,即旋转不改变图形的形状和大小.
“操作与思考”环节(1)是对旋转性质的进一步探究,通过图4的操作获得猜想,借助透明纸的可移动性,旋转任意的角度来进一步检验猜想.环节(2)是对性质的应用,先确定旋转中心,再借助透明纸进行验证.
“思考与画图”是对概念和性质的综合应用.有了前面两个环节的铺垫,此时学生可以脱离透明纸的辅助,利用获得的旋转的性质,熟练画出旋转后的图形.
二、从情感态度看:激发学生的学习兴趣
提起数学,很多人联想到的是数字、符号、定义、定理、计算、证明……很多学生对数学望而生畏,甚至讨厌数学.笔者认为,学生只看到了数学的一个方面,更为准确的说,是教师只为学生呈现了数学的一个方面,使得数学像置于X光下的妙龄少女,看到的只有骨骼.数学也有有趣和赏心悦目的一面,这一面可以改变学生对数学固有的认识,激发学生的学习兴趣,而实现这一转变的方式有很多,或许只用一张小小的纸片就可以实现.
案例2:设计轴对称图形.
活动1:欣赏.
(1)欣赏生活中的各种标志,观察哪些是轴对称图形?画出轴对称图形的对称轴.
(2)欣赏一组剪纸作品,观察哪些是轴对称图形?画出轴对称图形的对称轴.
(3)仔细观察这些轴对称的剪纸作品,说一说它们是如何剪出来的?
活动2:剪纸.
(1)取一张矩形纸片,将其对折后展开,沿着对折线画出如图7(1)所示的图案,再将其沿对折线折叠后,沿着图案的轮廓线剪下,展开后,你看到了怎样的图案?它是轴对称图形吗?为什么?

图7
(2)取一张彩色纸片,用上面的方法设计并剪出一个轴对称图形.
活动3:剪出有多条对称轴的轴对称图形.
(1)选取一张正方形纸片,按如图8所示的步骤折叠,在折叠后的纸片上画一个图案,沿着图案的轮廓剪下并展开,观察图案并思考:这个图案是轴对称图形吗?如果是,它有几条对称轴?

图8
(2)取一张彩色正方形纸片,仿照上面的方法设计并剪出一个有3条对称轴的轴对称图形.
设计轴对称图形是苏科版《义务教育教科书·数学》八年级上册第二章第三节的内容,在此之前学生刚掌握了轴对称与轴对称图形的概念、轴对称的性质.本节课旨在通过欣赏自然界和现实生活中的轴对称图形,帮助学生感受数学丰富的文化价值,使学生能够利用轴对称设计简单的图案.在实际教学中,很多教师将这一课时用很短的时间一带而过,甚至直接跳过.这样处理看似没有知识上的缺失,甚至节省了教学时间,但是却忽视了学生情感的共鸣、数学文化的熏陶,以及创新能力提升的机会.笔者按照上述三个环节开展教学,循序渐进地带领学生欣赏美、创造美,学生十分感兴趣,不仅巩固了知识,而且体会了数学中的对称美,更是发挥了各自的想象力和创造力,呈现了许多有寓意、有创造性的剪纸图案,对后续学习产生了积极的助推作用.
三、从能力培养看:培养学生的实践能力
《普通高中数学课程标准(2017年版)》指出,学生学习应当是一个生动活泼的、主动的和富有个性的过程.除了接受学习以外,动手实践、自主探索与合作交流同样是学习数学的重要方式.学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等过程.
案例3:探究无盖长方体纸盒的最大容积.
活动1:操作与比较.
取一张正方形纸片按如图9所示的方法进行操作.

图9
(1)与同伴制作的无盖长方体纸盒进行比较,估计谁制作的无盖长方体纸盒容积要大一些?
(2)猜想:在什么情况下,制作的无盖长方体纸盒的容积最大?
活动2:计算与发现.
(1)若正方形纸片的边长是10 cm,随着减去的小正方形边长的变化,所制成的无盖长方体纸盒的容积是怎样变化的?
(2)在上述计算过程中,你发现该纸盒的容积是如何变化的?你有何猜想?你还可以继续探究下去吗?试试看.
活动3:实践与应用.
(1)利用一张边长为60 cm的正方形纸片,制作容积最大的无盖长方体纸盒,如何制作?
(2)利用一张长30 cm、宽20 cm的长方形纸片,制作底面积为200 cm2的无盖长方体纸盒,请设计制作方案.
本实验是一个实践性强、探究味十足的数学实验.首先通过制作无盖的长方体纸盒,让学生直观感受到纸盒的容积有大有小,进而探寻影响无盖长方体纸盒容积的因素,为接下来的探究做准备.接着,通过计算初步验证:无盖长方体纸盒的容积随剪去的小正方形的边长的变化而变化,并从数据中发现变化规律,随后进一步探究、验证规律.最后,通过建立一元二次方程模型来解决实际问题.
四、从思维提升看:发展学生的直观思维
直观思维是不经过逐步分析,而迅速对问题的答案做出合理的猜测、设想或顿悟的一种跃进式思维.逻辑思维是人脑的一种理性活动,是把感性认识阶段获得的对于事物认识的信息材料抽象成概念,运用概念进行判断,并按一定逻辑关系进行推理,从而产生新的认识.逻辑思维具有规范、严密、确定和可重复的特点,是一种重要的数学思维.在实际教学中,常有忽视直观思维,过分重视逻辑思维的情况发生,考虑到初中生的年龄特征和思维发展水平,在学习中仍需借助直观感知来理解知识,这就需要教师创造合适的情境,借助恰当的实验工具,加以引导.
案例4:分割三角形.
活动1:分割等腰三角形.
通过折纸,分别将顶角为36°、顶角为90°、顶角为108°的等腰三角形分割成两个小等腰三角形.说说你的分割过程.
活动2:分割直角三角形.
(1)将普通的直角三角形纸片分割成两个小等腰三角形.探究这条折痕的长和直角三角形斜边长的关系,你有怎样的发现?再任取一张试试看,结论依然成立吗?
(2)将含30°角的直角三角形纸片分割成两个小等腰三角形.探究各条线段的长,你有怎样的发现?说明理由.
活动3:分割一般三角形.
(1)如图10所示的锐角三角形和钝角三角形纸片,分别在纸片上画一条线,将每个三角形分割成两个三角形,使其中一个是等腰三角形,试试看.这样的分割线最多能画多少条?并与同伴交流.
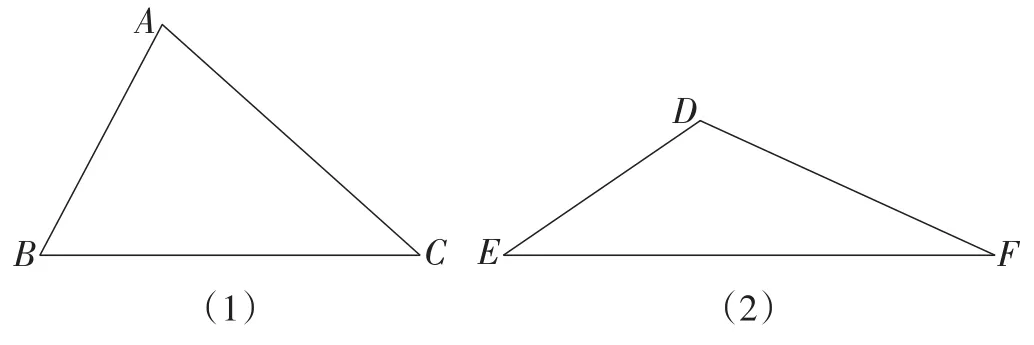
图10
(2)不同分类下产生的分割线会不会重合呢?在怎样的条件下会重合?借助几何画板软件验证你的猜想.
案例4中的三个实验活动均具有直观性、操作性等特点,且循序渐进,可以通过“观察—尝试—验证—说理”等过程完成探究.观察是一种直观感知,尝试是将感知付诸实践操作,验证是初步检验尝试的正确性,说理则跳出感性上升到理性,四个环节的思维活动水平逐步提高,活动3更是具有发散性和探究性,如何分类讨论?何时分割线重合?对学生思维品质的要求更高.
小小的纸片看似平常无奇却在数学实验中发挥着巨大的教育功能:促进知识的理解、激发学生的兴趣、提高学生的能力、提升数学思维、改进教学形式,等等.真正做到了从转变教师教的方式,到转变学生学的方式.实现从“学数学”到“做数学”到“玩数学”的转变,真正做到了手脑协同、启思明理、关注能力、提升素养.

