城市物流配送订单分配排序优化研究

师嘉欣，高更君

（上海海事大学 物流研究中心，上海 201306）

0 引言

随着经济的快速发展，城市物流配送已经成为城市经济发展与居民生活的重要支撑系统，需求日趋旺盛。为提高城市物流配送的整体效率、满足客户的多种差异化需求，如何对大量客户订单进行合理分配使配送时间最短已成为国内外学者研究的热点问题之一，典型的研究有：朱孟高[1]等面对庞大的客户规模，将同一路段的客户点和末梢客户点进行合并，提出集束式算法解决城市物流配送问题；王雪萍[2]在考虑车辆有容量约束的情况下，以配送时间最短为目标，运用节约算法对城市配送问题进行求解；Anna Franceschettia[3]等把城市配送问题转化为城市区域划分的问题，用动态规划算法求得时间最短的配送方案。这些研究通过对订单配送时间的优化为解决城市物流配送问题提供了思路，但都未考虑订单装载时间对整体配送效率的影响。订单货物的装载和配送是物流系统的重要环节，它们相互联系、制约，影响订单的整体配送效率。基于此，本文尝试综合考虑订单装载时间与配送时间对整体配送效率的影响，利用成组分批排序的理论和方法对解决资源和任务分配问题的优势来解决城市物流配送订单分配排序优化问题，以实现配送过程整体最优，从而提高整体配送效率和客户满意度。

1 城市物流配送订单分配排序问题描述

城市物流配送依托城配中心来完成客户的订单配送任务，在运营过程中城配中心面临着大量的订单配送需求，需要通过集货、分拣、装载和配送等物流作业，按客户的要求对订单货物有计划的运输并送到指定地点以完成订单配送服务[4]。本文研究的是一个城市配送中心为多个客户需求点提供配送服务的订单分配排序问题，具体可以描述为城市配送中心在满足客户订单需求及车载量限制等约束条件下，对客户订单进行分配，每批订单开始配送前有一个批订单货物装载时间，订单货物装载完成后，每辆车从配送中心出发对客户点完成服务后回到配送中心。要求确定合适的订单分配和客户服务顺序，使订单货物装载和配送的总完工时间最短，提高整体配送效率。

2 城市物流配送订单分配排序模型建立

2.1 排序论概述

排序论作为运筹学的一个分支，对提高效率、资源的开发和配置、工程进展的安排以及经济运行等方面都能起到辅助科学决策的作用，是解决资源和任务分配组合优化问题的一种理论和方法[4]。其中，成组分批排序理论是排序论中的一个组成部分，在成组分批排序理论中，每组工件在开始加工前，都需要一定的安装时间，而且安装时间会影响工件加工顺序，在加工过程中工件不允许中断，并且同一客户的工件不可以分批进行加工，与本文研究的装载和配送组合优化的订单分配排序问题比较相似。并且对于制造系统中多品种、多频次、小批量的工件加工需求，运用成组分批排序理论可以提高加工效率，实现资源最优调配，因此用成组分批排序理论解决本文研究的问题有一定的优势。

2.2 模型假设及参数设定

2.2.1 模型假设

为了便于建模，作出假设：

1）车辆型号相同，在配送过程中匀速行驶，不考虑道路拥堵问题；

2）客户的商品需求量和地点是已知的；

3）车辆的载货量有限，任何一个客户订单需求的物品总量不能超过车辆的载货量限制，订单物品可以混装；

4）不考虑车辆在客户需求点停留的时间，即到即卸；

5）每辆车从配送中心出发并返回配送中心；

6）一辆车可以为多个客户服务，但是一个客户不能由多辆车服务。

2.2.2 参数设定

参数设定如下：

1）N表示需要配送的订单集合，N=（N1，N2，…，Nn）；

2）M表示需要配送的车辆数，M=（M1，M2，…，Mm）；

3）X表示配送中心和客户需求点编号X=（0，1，2，…，x），其中0表示配送中心，其余的点为客户需求点x；

4）B表示订单的分批批数，B=（1，2，…，b）；

5）Q为车辆的最大载货量，以t为单位；

7）Yi表示在客户点i需要配送的货物量，以t为单位；

8）α表示车辆行驶速度；β表示装货的效率；

2.3 模型建立

根据本文提出的问题，将城市物流配送订单中的每个货物视为工件，车辆视为机器，将车辆在配送中心装载货物的时间视为工件的批安装时间，将车辆行驶到每个客户需求点的时间视为工件的标准加工时间，将车辆从一个客户需求点行驶到另一个客户需求点的时间视为工件的实际加工时间，以总完工时间最短作为目标，建立模型如下：

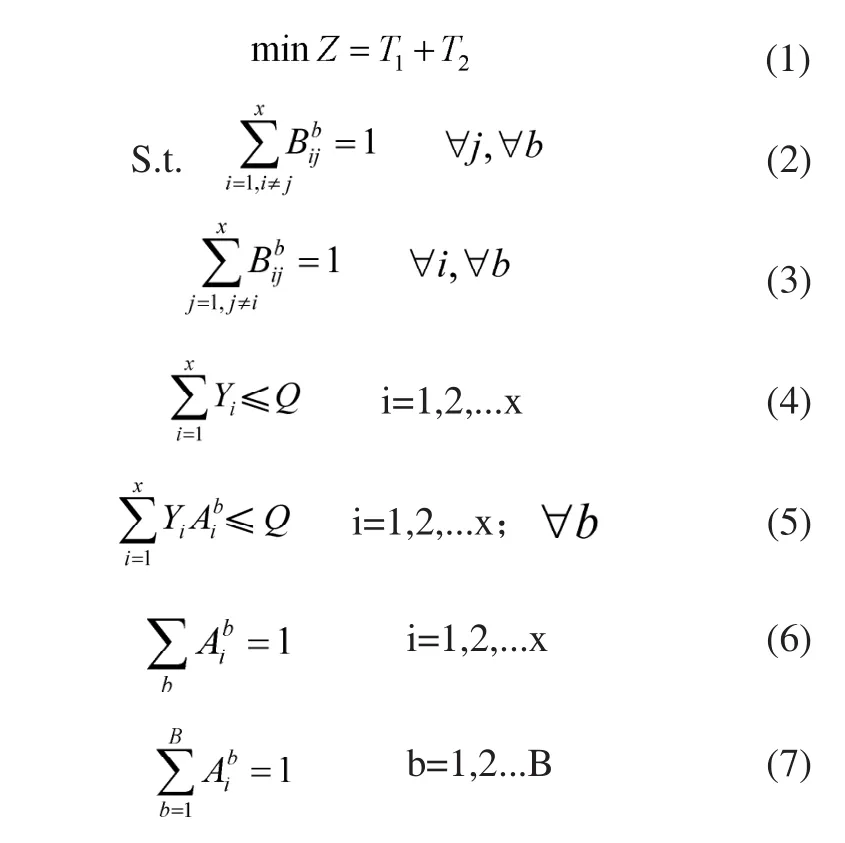
式(1)表示目标函数即总完工时间最短，T1为在配送中心装载货物的时间，即工件的安装时间之和；T2为车辆的总行驶时间，即所有工件的加工时间之和；式(2)、式(3)表示每批订单的配送路径都形成一个哈密顿回路，即每批工件在一个机器上加工完后机器停止工作；式(4)表示任意订单需要货物量都不能超过车辆最大载货量，即任意工件都可以在一台机器上完成加工；式(5)表示任意批次订单所需货物量都要低于该批次车辆的最大载货量，即车间每台机器的加工容量有限；式(6)、式(7)表示客户订单不可以分割，一个客户只能由一辆车服务，即同一客户的工件不能分批加工。

3 模型算法设计

启发式算法求解整数规划模型可以降低计算难度，提高计算效率，所以本文用启发式算法对模型进行求解，本文的启发式算法原理是首先把所有工件依次分配给机器得到初始可行解，然后再重复互换最大完工时间最大和最大完工时间最小的两台机器的工件，直到没有可改进的解，从而得到最优排序[6]。工件的交换方法和算法的具体步骤如下：

以M1和M2两台机器为例，如图1所示，则工件交换方法如下：

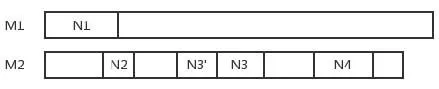
图1 工件交换图示

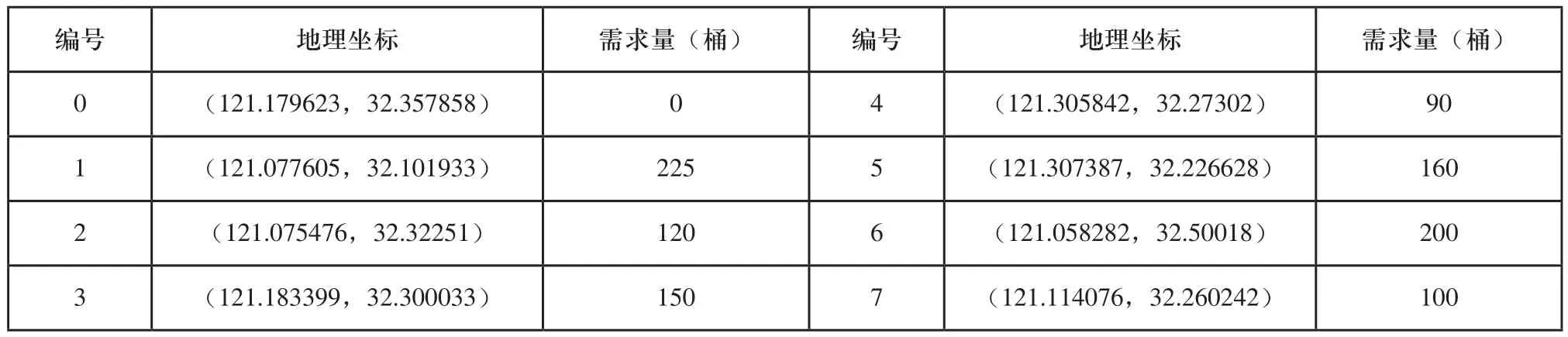
表1 配送地理位置及需求分布

通过上述交换方法，对于工件N1最多需要进行两次交换，使算法复杂度降低，提高了计算效率。

2）算法步骤

（1）将工件和机器依次编号，令N1为M1上的第一个工件。

（2）把剩下的工件依次分配给最先空闲下来的机器，当多台机器同时空闲下来时，优先选择编号小的机器，得到初始可行解。

（3）根据（2）中得到的工件顺序计算每批的安装时间和加工时间之和求得总完工时间，寻找互换后能使当前总完工时间变小的工件，若存在，转（4），否则转（5）。

（4）按照（1）中的交换方法将工件进行交换，交换完成后把两台机器上的工件顺序重新排列使总完工时间最小。

（5）寻找可互换的工件，若存在，则转（4）；否则，停止。

根据本文建立的城市物流配送订单分配排序模型，在LINGO11.0上进行程序设计，运用上述启发式算法求解可以得到总完工时间最小的订单分配排序方案。

4 算例模拟

为了验证模型和算法的有效性，假设有一个配送中心向七个客户送桶装水，配送中心与各个客户的地理位置和每个客户的需求如表1所示。已知配送中心有三辆型号相同的车，每辆车的最大载重量为10t，每桶水为0.02t，装货效率为12t/h，车辆的行驶速度为50km/h，车辆完成配送后返回配送中心[2]，通过合理的订单分配排序方案，使总完工时间最短。

运用LINGO 11.0对算例求解，得到最优订单分配排序方案如图2所示，客户订单的分配排序方案为：第一批0-7-1-0；第二批0-2-6-0；第三批0-3-4-5-0，总完工时间为4.798h，则每个订单的平均完工时间为（0.778+1.1 48+0.741+1.149+0.789+1.027+1.133）/7=0.966h。

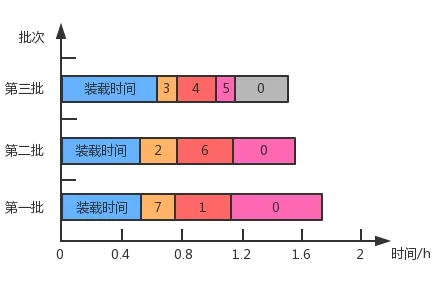
图2 订单分配排序方案

由文献[2]的研究成果可知若加上每批订单货物的装载时间，则通过节约算法对订单分配优化的总完成时间为2.678+1.249+1.125=5.052h，每个订单的平均完工时间为（1.09+1.196+1.708+0.825+0.977+1.127+1.249+0.729）/7=1.272h。可得出本文研究的对客户订单装载时间和配送时间组合优化所得到的总完工时间小于只对订单配送时间优化所得到的总完工时间，同时可以降低每个订单的平均完工时间，减少城市配送中心车辆的占用和其余客户订单的等待时间，实现资源的最优调配，提高整体配送效率和客户满意度。

5 结论

城市物流配送问题的解决能够促进城市经济健康快速发展，提高居民生活水平。通过本文的研究，建立了城市物流订单配送总完工时间最短的目标函数模型，运用启发式算法对算例进行求解，结果表明对客户订单的装载时间和配送时间组合优化可以提高订单整体配送效率，减少城市配送中心车辆的占用和其余订单的等待时间，实现资源的最优调配，希望为以后城市物流订单配送问题提供新思路。