运筹学在施工企业机械管理中的应用研究

孟凡磊，庄荟燕

（1.中交一公局第四工程有限公司；2.广西奕皇科技发展有限公司，广西 南宁 530000）

随着我国现代化建设的深入推进，大量建设工程纷纷展开，机械化施工的应用更加广泛，以道路和桥梁施工为例，大面积使用机械化施工，如推土机、装载机、平地机、挖机、土方车、泵车、架桥机、塔式起重机等。在各种类型工程的施工建设过程中，加强机械设备的维修与管理，选择合理的设备更换、维修方案，改善设备的使用状况，不仅保证了施工质量和工期，还降低了机械成本，最大限度的提高了企业的经济效益。

1 运筹学概述

运筹学是利用数学方法研究各种系统优化问题的学科，是一种非常有效的数学工具。其可以针对实际工作，提炼并构建数学模型，以求解最优方案形式制定相应的优化措施。运筹学在工程建设领域中有很大的应用空间，如投标项目的选择；生产计划的制定；人、材、机各项费用的控制；采购和库存计划；设备的更新问题；工程投标决策问题；资金运作问题等。常用的运算研究方法包括排队论、线性规划、图网法、对偶论、存储理论、决策理论等。其理论和方法在建设项目管理活动领域中已得到普及，产生十分可观的经济效益。本文对运筹学在设备维修、更新中的应用进行了举例分析和论述，并探讨了其在工程机械管理中的推广应用。

2 利用排队论对设备维修问题进行简单分析

排队论，或称随机服务系统理论，是运筹学中理论、应用都比较成熟的分支。通过对服务对象到达和服务时间的统计研究，得到这些定量指标（等待时间、排队长度、忙期长短等）的统计规律，然后对服务系统进行改进和优化，使之能够满足需要，又能有良好的经济指标或其他指标。

排队论模型在设备管理中可应用于维修调度、故障排除等方面。机械设备的维修可以看作需求源为有限的排队模型（M/M/1/∞/m），这种系统在机械维修中使用较多。假设对系统的需求是m，当排队系统中有n个需求时，服务系统外的新潜在需求减少到m-n个。假设每个单位时间、每个需求到达排队系统的概率或平均次数都是相同的λ，然后是系统外需求对系统的平均到达率λn=(m-n)λ。显然，平均到达率随着系统n的状态而变化。

例如施工现场有5台混凝土泵车。每辆泵车的连续运行时间呈负指数分布，平均连续运行时间为120min。1名修理工负责为泵车更换清理泵管，每次更换或清理时间服从负指数分布，每次平均15min。求该排队系统的数量指标Po、Ls、Lq、Ws、Wq和 τ。

解决方案。假设每小时每台泵车的平均故障次数服从泊松分布，因此排队系统为系统，其中：

λ=1/120，m=5，μ=1/15，ρ=λ/μ=0.125

（1）工人空闲的概率。

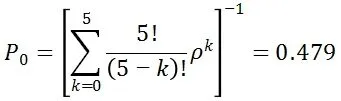
（2）出故障的平均泵车数。

（3）等待修理的平均泵车数。

（4）平均停工时间。

（5）平均等待修理的时间。

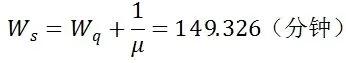
（6）泵车利用率。

3 利用网络图最短路线方法解决机具更新问题

Dijkstra算法指求解。指定两点Vs、Vt之间的最短路径，或是从指定点Vs到另外一点的最短路径，现在来说是Wij≥0下求最短路问题的最好方法。

其基本思路基于以下原理：假设P是从Vs到Vt的最短路径，Vi是P中的一个点，则Vs到Vi的最短路径就是Vs沿P到Vi的那条路。

采用标记法：T标记与P标记。T标记为暂定的标记，P标记为永久性标记。给Vi点一个P标记时，该标记表示从Vs到Vi点的最短路权，并且该点的标记不再变化。当给出T标记时，T标记表示从Vs到Vi点的最短路权的上限，这是其临时标记。凡没有得到P标记的点都有T标记。算法的每个步骤都将某个点的T标记更改为P标记。当终点Vt得到P标记时，结束以上的计算。

例如在建筑工地使用1台设备，并且在每年年初决定是否更新。若购买新设备，则必须支付购买金额；若使用老设备，则要支出维修费用。尝试制定5年更新计划，以最大限度地降低总成本。

假设已知在不同年份购买的设备和不同机器役龄时的残值和维护成本，如表1所示。

表1

解：将该问题化为最短路问题。

Vi表示第i年购买了一台新设备，虚设点V6表示第5年结束；弧（Vi、Vj）表示在第i年开始的时候购买的设备一直使用到第j年开始（第j-1年年底）；弧（Vi、Vj）旁的数字表示第i年购买的设备，一直使用到第j年初所需支付的采购、维修的全部费用。设备更新问题就变为求从V1到V6的最短路径，具体计算结果如表2、图1所示。

表 2 万元

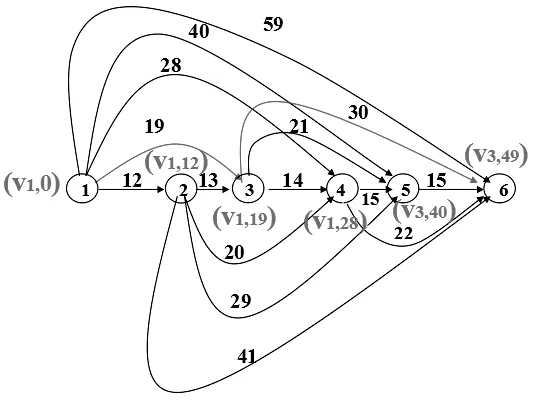
图1

由计算结果可知，v1→v3→v6为最短路，路长为49。那么第1年、第3年初各采购一台新设备最划算，5年的支出之和为49万元。

4 结语

综上所述，将机械设备管理中的实际问题构建成数学模型，然后应用运筹学思维，用一些数学方法进行定量分析，求得合理的工作效率、费用等最佳方案，是机械管理中一种非常有效的方法和手段。由此可知在机械设备管理的实际工作中，及时总结归纳遇到的各类问题和数据，构建合适的模型，并运用一些科学的方法加以分析，使解决方法更经济、更效率，即可提高施工企业的机械管理水平。