基于混合核的超球面支持向量机车牌字符识别
胡 霖
(中国石油大学胜利学院 教学科研处,山东 东营 257000)
车牌字符识别算法直接影响车牌识别的效果,目前最常用的方法有以下3种:模板匹配、人工神经网络以及支持向量机[1]。其中,支持向量机方法因可以有效避免局部极值问题得到更广泛应用。对支持向量机在实际应用中的研究,主要采用以下两种方法:一是与另外的分类算法相组合;二是优化核函数提高其自身性能。但当把经典支持向量机推广到多分类领域时[2-3],计算复杂程度均较高。Tax[4]等人首次采用球体形式来包含样本数据。朱美琳[5]等人研究将这种球体形式加入支持向量机,改进其分类策略。施隆照[6]等人提出一种组合支持向量机方案,算法采用一类超球面和标准SVM进行车牌字符识别,过程较繁琐,且默认采用径向基核作为核函数,没有深入论证分类正确率与核函数选择关系问题。在车牌字符识别应用中,超球面支持向量机虽然能够获得比传统支持向量机更好的分类效果,但对其核函数的选取仍然没有成熟方案。针对以上不足,本文提出一种超球面混合核支持向量机(MHS-SVM),在分析了超球支持向量机分类计算方法和各种核函数的基础上,采用多项式核函数与径向基核函数两者的线性组合构建混合核函数进行优化。该算法首先对选取的车牌字符图片进行特征提取,然后分别将单一径向基核函数和混合核函数应用到超球面支持向量机决策函数中,找到径向基核函数参数和线性组合交叉概率的最优取值。通过对加州理工学院Computational Vision研究小组Cars 1999 (Rear) 2数据集[7]进行测试,最后将本文算法结果与已有方案进行比对,算法在车牌字符识别上提高了识别正确率,同时保持了较高的识别速率。
1 超球面+核函数
1.1 超球面支持向量机
超球面支持向量机目前得到了越来越广泛的关注,相比于传统支持向量机,它力求找到一个半径最小的超球面来分类数据,而不是为待分类样本寻找超平面[8]。该方法将数据映射到Hilbert空间,可通过改进的多类分类策略获得比传统支持向量机更好的学习能力和分类效果。
超球面支持向量机将同质数据尽量用半径最小的超球面来包含,数据空间被分割成了几个超球,类似在立体空间中的一个个肥皂泡。图1以三超球重叠来示意样本分布。构造出的每一个超球对应一类样本数据,采用这种方案可以使算法的复杂性降低,明显减少二次规划难度从而使大样本处理成为可能。另外,如果针对新来的样本需要新增类别,只需添加一个该类别的新超球,大大提高了可扩展性。

图1 样本分布在重叠三超球中的情况
假定现在使用超球面支持向量机对样本进行k类划分:k个元素集维度设为n,对于每个集合用Vm表示,找出一个最小超球面,vm是最小超球面的球心,Rm是最小超球面的半径,使得最小的超球面包含所有采样点xim。目标函数为
(1)
利用Lagrange优化方法转化为对偶问题:

(2)
目标是拉格朗日乘数。将公式(2)中的内积运算用核函数代替,推导出用于特征空间中分类超球的二次规划公式:
为验证本文提出的空间圆弧拟合优化方法的准确性,对图2中的数据点云,用基于拉格朗日乘子法的空间圆弧拟合方法进行拟合。分别进行2组各5次拟合实验,其中一组应用了RANSAN算法剔除错误点,拟合结果如表3所示,分析结果如图4所示。同时,将本文优化方法与传统空间圆弧拟合方法进行比较,拟合结果如表4所示,分析结果如图5所示。
(3)
决策函数力求找到样本点x到球心的最小距离,具体函数如下:
fm(x)=[K(x,x)-2K(x,am)+K(am,am)]-(Rm)2,
m=1,…,k.
(4)
通过将准备好的车牌字符集代入公式(4)中训练,可以标识出各类超球的相对位置。在实际应用中,用决策函数求出新样本点与各类超球的距离,距离最小的超球所代表的类型即是该样本点的类型。核函数的选取会直接影响最终的分类效果。接下来将详细论证混合核函数的构造过程。
1.2 核函数
传统支持向量机处理的是线性样本数据,但数据往往并不是理想化的,对非线性状态的数据的识别和分类是有必要的。核函数可以将低维的非线形状态的数据转映为高维,克服低维空间的不利因素,从而成功地构筑出超平面。内核函数的选择会对支持向量机的执行效果产生很大的影响。
核函数计算如公式(5)所示:
K(X,Z)=〈ω(X)·ω(Z)〉.
(5)
线性核、多项式核、Sigmoid核以及径向基核是核函数的4种主要类型[9]。
(1)线性核:

(6)
公式(6)表示线性核计算内积来对数据进行处理。经过这种处理可以把原始区域和映射后区域的数据进行整合。
(2)多项式核:

(7)
公式(7)计算多项式空间内积,注重整体的数据。为了降低计算复杂度,往往需要将多项式中高维的计算转换成低维。
(3)Sigmoid核:

(8)
公式(8)核函数关注全面最优样本数据。
(4)Gauss径向基核(RBF):

(9)
公式(9)性能受参数选择和局部扰动,映射维度可以任意。特征空间参数越小映射维度越低,参数越大拟合度越严重。自由度高和可控性强使得径向基核在实际应用中被广泛采用。设置较小的参数可以有效地提高分类的能力,但同时泛化能力会降低。
RBF学习性能较强,但泛化不足,而多项式核泛化性能较强,将两者结合起来构成混合核,可进一步提高超球面支持向量机分类性能。
对混合核创建一个矩阵M=mij,选择多项式核和RBF进行线性的组合[10],矩阵单个元素表达式为
mij=mmulti(xi,xj)=ampoly(xi,xj)+(1-a)mRBF.
(10)
式中,a为权值,a∈(0,1)。
通过式(10)替换式(4)中的核函数部分,将上述MHS-SVM算法应用到车牌字符识别中,对径向基核函数的参数以及线性组合权值选取不同区间的值,确定不同参数对识别结果的影响,抉择出最终解。
2 特征提取
2.1 数据来源
车牌图片数据均取自加州理工学院Computational Vision研究小组Cars 1999 (Rear) 2数据集,样例图片如图2所示。数据集中包括126张汽车车牌图片,每张图片采用896×592的jpg格式,每个车牌包含7个字符。将汽车车牌图片随机排序后分成X、Y、Z三个图片数量相同的样本集,首先训练Y、Z,用X来测试结果;第二次训练X、Z,用Y来测试结果;最后选取X、Y作为训练样本,Z作为测试样本;三次试验得到识别率的平均值作为试验的最终结果。

图2 Cars 1999 (Rear) 2数据集样例
归一化采取简单处理。将牌照字符图像存储到计算机中采用的是矩阵形式,字符‘O’存储的矩阵(以9*9为例)如图3所示。要方便支持向量机利用其进行训练和试验,有必要将它们降维转换成一维形式,为保证识别的准确性,计算的简单性和硬件的易于实现特性,将字符矩阵转换为一维矢量,根据直线拼接提取特征。
对上述字符‘O’的直线拼接即是从第一行开始,每一行链接到前一行最后一个元素而构成一维矢量。这样处理的一维矢量虽然很长,但因为核函数的选取并没有带来计算的增加,而且避免了复杂处理过程中字符矩阵的复杂处理和特征损失。

图3 无干扰情况下字符‘O’的9*9存储矩阵
3 试验与分析
3.1 试验过程
首先对训练样本集中的字符进行分割和特征提取转换为一维矢量。第一步将公式(10)的权值a设置为0,仅用RBF作为核函数,测试结果如表1所示。表中X|YZ表示的是将Y、Z作为训练集,X作为测试集,其他类似。从测试数据可以看出,选定γ=1.8,径向基核支持向量机具有最优的识别正确率。
第二步,在γ值确定的情况下,当权值a分别取不同值时,测试结果表明,引入混合核以后的算法在识别正确率上有所提升(表2)。

表1 纯径向基核测试数据

表2 线性组合不同权值下测试数据
由上述试验数据得出参数γ与a对算法识别正确率影响曲线如图4,5所示。
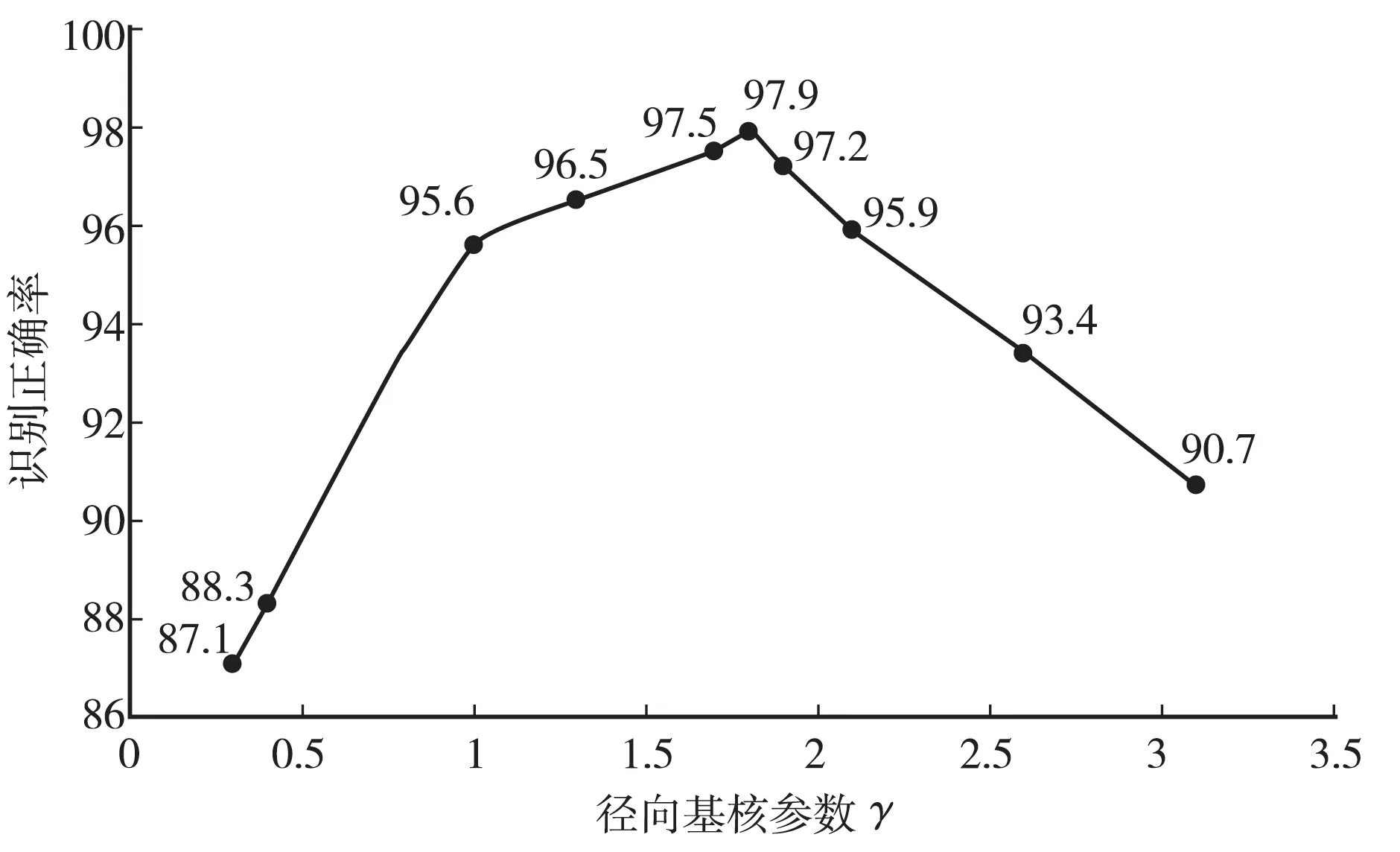
图4 纯径向基核超球平均识别正确率

图5 混合核超球平均正确率
3.2 试验分析
通过3.1中试验步骤,针对测试数据集最终将径向基核参数调为1.8,权值为0.35获取最优识别正确率。表3中列出本文测试结果与其他算法的对比情况。

表3 与其他算法对比情况
可以看出,本文提出的MHS-SVM算法较文献[6]和[11]识别正确率有所提高。由于引入了多项式核函数计算量增多,识别时间较文献[6]稍有增加,但比文献[11]已有较大改进。
4 结束语
针对支持向量机在车牌字符识别中应用存在的问题,利用基于混合核的超球面支持向量机进行改进。新算法识别速率快,使用多项式核与径向基核线性组合方式,并在此基础上试验决出针对车牌字符识别的最优核参数与线性组合权值,进一步提高了识别正确率。下一步研究方向将尝试其他核函数组合方案,并结合结构化学习对核参数进行深度优化。

