电磁感应中焦耳热问题的题型归类与解题策略

湖南

电磁感应中的焦耳热问题是电磁感应知识学习中的一个重难点。此类问题主要考查考生的理解能力、推理能力以及综合分析能力，对考生的物理思维能力要求较高。在求解过程中需要把握以下几点：

(1)明确电磁感应的类型，分析清楚闭合回路的磁通量如何变化，回路中形成的是动生电动势还是感生电动势。通过法拉第电磁感应定律或者切割模型公式计算电动势的大小，结合闭合电路欧姆定律计算回路的电流大小。

(2)明确研究系统中的能量转化过程，分析清楚是何种形式的能量转化成闭合导体回路中的电能。

(3)注意题中需要求解的是哪一时间段内的焦耳热，同时注意求解的是整个闭合回路产生的焦耳热还是某一个电阻产生的焦耳热。分析清楚后，通过焦耳定律或者能量守恒定律求解电路中相应的焦耳热。

1.电流恒定

【例1】做磁共振检查时，对人体施加的磁场发生变化时会在肌肉组织中产生感应电流。某同学为了估算该感应电流对肌肉组织的影响，将包裹在骨骼上一圈肌肉组织等效成单匝线圈，线圈的半径r=5.0 cm，线圈导线的横截面积A=0.80 cm2，电阻率ρ=1.5 Ω·m，如图1所示，匀强磁场方向与线圈平面垂直，若磁感应强度B在0.3 s内从1.5 T均匀地减小为零，求(计算结果保留一位有效数字)

(1)该圈肌肉组织的电阻R；

(2)该圈肌肉组织中的感应电动势E；

(3)0.3 s内该圈肌肉组织中产生的热量Q。

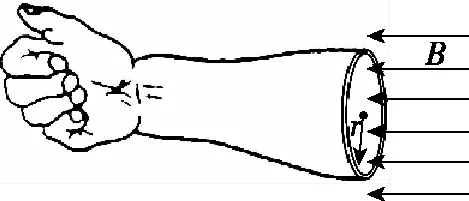
图1

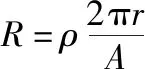
解得R=6×103Ω

解得E=4×10-2V

(3)由焦耳定律知Q=I2RΔt

解得Q=8×10-8J

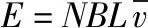
2.正(余)弦交变电流

图2

【解析】由题知，金属棒产生的瞬时感应电动势满足

电动势的最大值为Em=BLv0

由焦耳定律知R上产生的热量Q=I2Rt

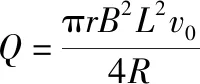
3.非正(余)弦规律变化电流

【解题策略】当闭合导体回路中的电流不是恒定电流，同时也不是正(余)弦交变电流时，直接利用焦耳定律Q=I2Rt难以求解。此时，求解回路中的焦耳热往往需要通过能量守恒定律Q=ΔE其他或者利用电路中总焦耳热等于电路中克服安培力做功的大小，即Q=W求解。

【例3】如图3所示，在匀强磁场中有一倾斜的平行金属导轨。导轨间距为L，长为3d，导轨平面与水平面的夹角为θ，在导轨的中部刷有一段长为d的薄绝缘涂层。匀强磁场的磁感应强度大小为B，方向与导轨平面垂直。质量为m的导体棒从导轨的顶端由静止释放，在滑上涂层之前已经做匀速运动，并一直匀速滑到导轨底端。导体棒始终与导轨垂直，且仅与涂层间有摩擦，接在两导轨间的电阻为R，其他部分的电阻均不计，重力加速度为g。求：

(1)导体棒与涂层间的动摩擦因数μ；

(2)导体棒匀速运动的速度大小v；

(3)整个运动过程中，电阻产生的焦耳热Q。

图3

【解析】(1)在绝缘涂层上，导体棒受力平衡有

mgsinθ=μmgcosθ

解得μ=tanθ

(2)在光滑导轨上，导体棒产生感应电动势为E=BLv

由安培力公式知F安=BIL

导体棒匀速运动时，由受力平衡知F安=mgsinθ

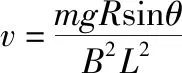
(3)导体棒与涂层摩擦产生的热量为QT=μmgdcosθ

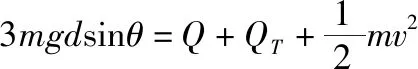
联立解得，电阻产生的焦耳热

【点评】导体棒从静止开始下滑过程中，进入涂层前做加速度逐渐减小的加速运动，当导体棒受到的安培力与导体棒所受重力沿导轨向下的分力平衡时，导体棒开始做匀速运动。进入涂层前，闭合回路形成的为非正(余)弦规律的电流。导体棒在绝缘涂层上运动时，闭合回路无感应电流。导体棒穿过涂层继续沿导体向下匀速运动的过程中，闭合回路产生恒定电流。因此求解整个过程闭合回路中电阻R产生的焦耳热，不能直接利用焦耳定律Q=I2Rt求解，需要利用能量守恒定律求解。导体棒下滑过程中，减小的重力势能转化为导体棒自身的动能、导体棒与涂层摩擦产生的内能以及闭合导体回路中的焦耳热。在利用能量守恒定律解决电磁感应中的焦耳热问题时，需要注意研究系统能量转化的途径及大小，同时注意是否有摩擦。

【例4】如图4所示，两条平行的金属导轨相距L=1 m，金属导轨的倾斜部分与水平方向的夹角为37°，整个装置处在竖直向下的匀强磁场中。金属棒MN和PQ的质量均为m=0.2 kg，电阻分别为RMN=1 Ω和RPQ=2 Ω。MN置于水平导轨上，与水平导轨间的动摩擦因数μ=0.5，PQ置于光滑的倾斜导轨上，两根金属棒均与导轨垂直且接触良好。从t=0时刻起，MN棒在水平外力F1的作用下由静止开始以a=1 m/s2的加速度向右做匀加速直线运动，PQ则在平行于斜面方向的力F2作用下保持静止状态。t=3 s时，PQ棒消耗的电功率为8 W，不计导轨的电阻，水平导轨足够长，MN始终在水平导轨上运动。求：

(1)磁感应强度B的大小；

(2)t=0～3 s时间内通过MN棒的电荷量；

(3)求t=6 s时F2的大小和方向；

(4)若改变F1的作用规律，使MN棒的运动速度v与位移x满足关系：v=0.4x，PQ棒仍然静止在倾斜轨道上。求MN棒从静止开始到x=5 m的过程中，电路中产生的焦耳热量。

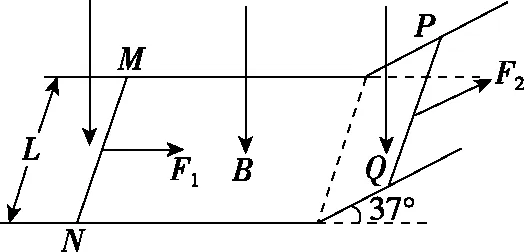
图4

【解析】(1)当t=3 s时，设MN的速度为v1，由匀变速运动公式知v1=at=3 m/s

由电磁感应规律知E1=BLv1

由闭合电路欧姆定律知E1=I(RMN+RPQ)

由电功率公式知P=I2RPQ

联立解得B=2 T

回路磁通量变化ΔΦ=BLx

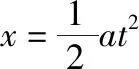
代入数据解得q=3C

(3)当t=6 s时，设MN的速度为v2，由匀变速运动公式知v2=at=6 m/s

由电磁感应规律知E2=BLv2=12 V

由安培力公式知F安=BI2L=8 N

规定沿斜面向上为正方向，对PQ进行受力分析可得

F2+F安cos37°=mgsin37°

代入数据得F2=-5.2 N(负号说明力的方向沿斜面向下)

(4)MN棒做变加速直线运动

由速度公式v=0.4x①

电动势公式E=BLv②

安培力公式F安=BIL④

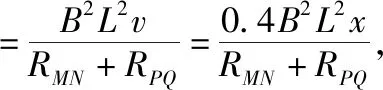
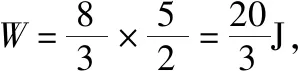
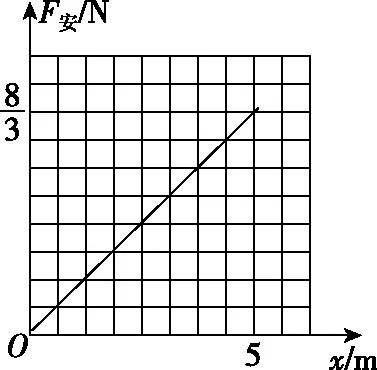
图5