基于图像自相似性的多尺度稀疏表示肺4D-CT图像超分辨率重建

王婷婷，张煜

1.南方医科大学南方医院设备器材科，广东广州510515；2.南方医科大学生物医学工程学院，广东广州510515

前言

四维计算机断层摄影（Four-Dimensional Computed Tomography,4D-CT）能够真实准确地反映靶区的运动范围及动态特征，被广泛地应用于肺癌的精确放射治疗之中并取得良好的效果［1］。然而，CT 的高剂量照射特性以及持久的扫描时间，致使数据沿纵向（Z轴方向）无法实现密集采样，导致数据层间分辨率远低于层内分辨率，造成各项数据异性，不仅影响图像可视化而且妨碍数据分析［2-3］。超分辨率（Super Resolution,SR）重建算法是一种提高肺4D-CT 图像分辨率的有效方法。将数据中不同相位、对应位置的图像作为多“帧”低分辨率（Low Resolution,LR）图像输入，经过SR重建处理，获得高分辨率（High Resolution,HR）输出图像。

本研究提出一种基于图像自相似性的多尺度稀疏表示SR重建方法，它是一种基于机器学习的重建算法［4-6］，主要解决以下两大难点：（1）基于稀疏表示的SR重建方法，一般需要相对应的HR和LR图像块两两组对作为训练集，以训练得到反映HR 和LR 图像之间关系的字典。但是对于肺4D-CT 图像而言，各项数据异性致使无法获取冠矢状面的HR 图像。在此种情形下，该如何构建训练集数据？（2）考虑到肺4D-CT 图像的解剖结构特征存在于不同尺度之下，应该如何选取图像块的大小，才能做到同时捕获不同尺度下的解剖信息？针对第一个问题，笔者引入自相似性的概念。图像自相似性［7］是源自于对图像的观察，发现一些细小的结构在整幅图像中重复出现。此概念已经被广泛应用到图像压缩［8］、图像复原［9］、非局部均值去噪［10］以及SR 重建［11］中。我们探索发现，肺4D-CT 数据冠矢状面图像和横断面图像不同尺度下的组织结构均存在一定的相似性。因此，笔者利用横断面图像来代替冠矢状面图像，构成HR 和LR 图像块对，作为训练集。具体内容将在第1.2 节中详细阐述。针对第二个问题，引入多尺度策略。图像多尺度分析最早可以追溯到1980年，源自于高斯和拉普拉斯金字塔的提出［12］。鉴于多尺度分析的优越性，大量算法引入此策略构建不同的多尺度 字 典，典 型 的 包 括Wavelets［13］、Contourlets［14］、Curvelets［15］等。笔者根据四叉树原理将“根”图像块划分为各个尺度的子图像块，并建立全局多尺度字典，详细内容将在第1.3节中具体介绍。

不同于基于模型的SR 重建算法，本研究算法不仅能避免运动估计，更能够改善HR图像细微结构的显示质量。对比单一尺度稀疏表示的SR算法，本研究的多尺度算法能有效地捕获肺部不同尺度下的解剖结构特征，重建出细节信息更为丰富的HR 图像。同时，量化评价指标也体现了本研究算法的优越性。

1 材料与方法

1.1 算法综述

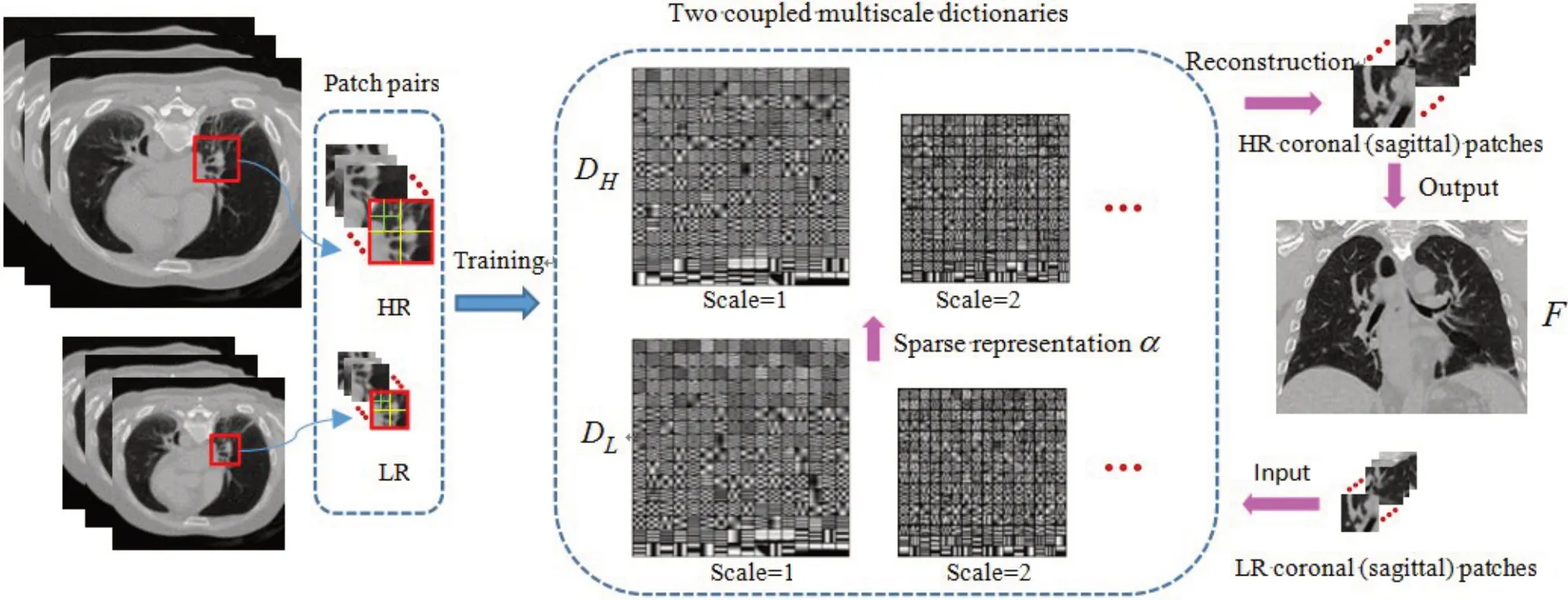
图1 基于图像自相似性的多尺度稀疏表示肺4D-CT图像SR重建算法示意图Fig.1 Overview of self-similarity-based multiscale sparse representation for lung 4D-CT image super-resolution reconstruction

第一步：利用横断面图像组成HR 和LR 图像块对构成训练集，训练得出成对的全局多尺度HR字典DH和LR 字典DL；第二步：输入的每一个LR 图像块PLi，寻求其经过LR字典DL表示后的稀疏系数α，由该系数及HR字典DH重建出此LR图像块对应的HR图像块PHi。最终，通过拼接所有的HR图像块以输出完整的HR图像。

1.2 肺4D-CT图像自相似性

本节中，结合后续依照四叉树原理所构造的多尺度分析，分别探究了图像块尺寸为16×16、8×8和4×4 的冠矢状面图像同横断面图像之间的自相似性［16］。利用结构相似性（Structure Similarity,SSIM）这一指标来度量图像块之间的相似性，其计算公式可以表示为：

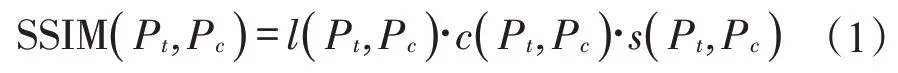
其中，Pt表示横断面图像块，Pc表示冠矢状面图像块，l(Pt,Pc)、c(Pt,Pc)、s(Pt,Pc)分别为：

其中，μ(Pt)、μ(Pc)分别表示图像块Pt和Pc的均值，σ(Pt)和σ(Pc)分别为Pt和Pc方差，σ(Pt,Pc)为Pt和Pc的协方差，C1、C2、C3均为常数。

图2给出冠矢状面图像同横断面图像之间自相似性的验证结果。其中，图2a 显示的是针对肺4D-CT 数据自相似性的量化评价结果。对于大小为16×16的图像块来说，74%的冠矢状面图像块能够在横断面上找到至少一个相似块；而能够找到50 个相似块的比例占到了55%。随着图像块尺寸的减小，该比例也在显著提高。当图像块大小为4×4 时，95%的冠矢状面图像块能够在横断面上找到20 个相似块。图2b给出冠矢状面图像同横断面图像之间自相似性的图像块示例。其中，冠状面与横断面的相似结构用红色方框标出；矢状面与横断面的相似结构用黄色方框标出。

图2 冠矢状面图像同横断面图像之间自相似性的验证结果Fig.2 Verification result of cross-scale self-similarity between coronal/sagittal images and transverse images

由此，笔者通过实验从定量和定性两个方面对冠矢状面图像同横断面图像之间的自相似性进行验证。基于此相似性，面对缺失冠矢状面HR图像的情形，笔者采用横断面HR和LR图像块作为训练集，来联合训练HR和LR字典。

1.3 多尺度稀疏表示SR重建

考虑到肺部图像解剖结构特征存在于不同尺度之下的数据特性，引入多尺度策略，采用四叉树划分原则［17］，构建多尺度图像块，利用基于稀疏表示的SR重建算法［18］，以横断面HR和LR图像块作为训练集，联合训练得出一对全局多尺度字典：HR 字典DH和LR 字典DL，并使得每一对HR 和LR 图像块具有相同的稀疏系数，而后对输入的LR图像块寻求其经LR 字典DL表示后的稀疏系数，直接由该系数及HR字典DH来估计得到相应的HR 图像块，实现基于图像自相似性的多尺度稀疏表示肺4D-CT 图像SR重建。

1.3.1 多尺度模型 如图3所示，根据四叉树原理将“根”图像块依次向下划分，得到各个尺度下的子图像块。假设“根”图像块的大小是n，则依照四叉树原则其子图像块的大小为其中s=0,1,…,S-1表示四叉树的深度，S表示尺度的个数。

对于尺度s来说，四叉树上共存在4s个位置。Ds∈Rns×ks表示尺度为s下任意一个位置的字典，该字典由ks个原子构成，每个原子是维数为的列向量。为了能够同时抓取多尺度数据特性，需要构建一个全局含有所有尺度下各个位置信息的字典D∈Rn×k。因此，对于多尺度字典D而言，它共含有个原子。

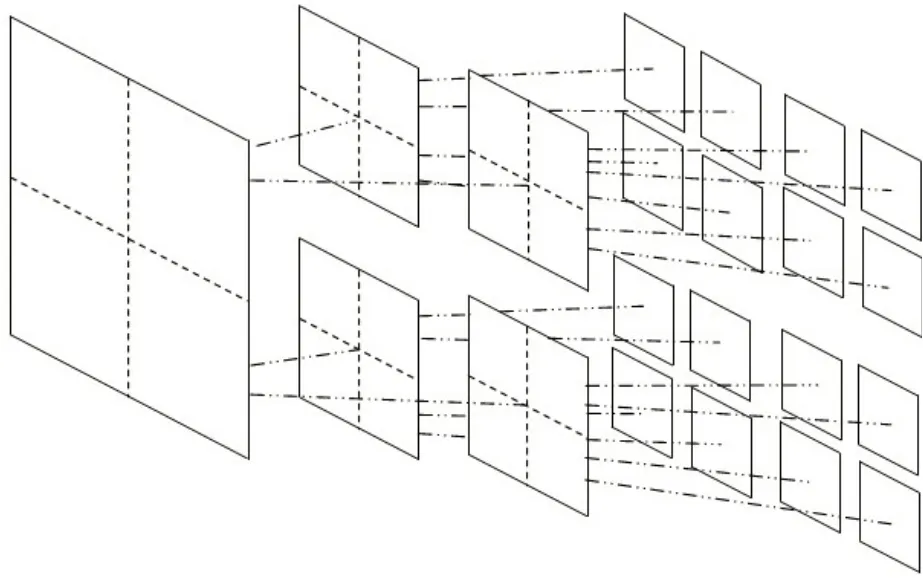
图3 四叉树分块方式示意图Fig.3 Quad-tree model selected for the proposed multiscale framework

由于尺度s的不同，构成单个尺度字典Ds的原子维数ns会发生相应变化。在全局多尺度字典D中如何设定原子的维数呢？笔者设定原子的维数为n，对于维数为ns=的原子，用零将其填满成n维。图4给出尺度个数S=3的全局多尺度字典中不同尺度下的原子示例。

图4 尺度个数S=3的全局多尺度字典中不同尺度下的原子示例Fig.4 Example of multiscale global dictionary atoms with 3 scales

1.3.2 SR重建 通过联合训练阶段，学习得到成对的全局多尺度HR 字典DH和LR 字典DL。它们可以使得训练集中成对的HR和LR图像块具有相同的稀疏系数，稀疏编码问题表示如下：

其中，XH={x1,x2,...,}xm表示从训练集取样的一系列HR图像块，YL={y1,y2,...,}ym表示与之对应的LR图像块，XH和YL构成了成对的训练集图像块为l0范数，它表示非零项的个数。Z分别为图像块XH和YL的稀疏表示系数矩阵。N和M分别表示HR和LR图像块向量形式下的维数。可以将式（5）改写为：

其中，

由于目标函数式（6）关于自变量Dc和Z为非凸函数，无法采用一般优化算法有效求解。但是二者中若一项固定，那么对于另一项来说，上述目标函数是凸函数。因此，一般采用两步迭代的方法求解。初始化字典Dc之后，循环进行稀疏编码阶段和字典学习阶段，直到目标函数收敛或达到预设的迭代次数为止。

（1）稀疏编码：首先固定全局多尺度字典Dc，通过OMP 算法计算获得训练集中“根”图像块Xc的稀疏表示系数矩阵Z：

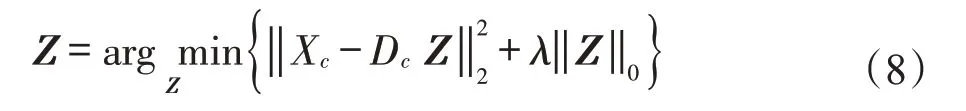
OMP 算法在计算“根”图像块Xc的稀疏系数时，是针对“根”图像块下的每一个尺度依次计算的，从s=0 到s=S-1，在同一尺度下再逐一计算每一个位置，共计4s位置。

（2）更新字典：与稀疏编码的方式相同，更新字典中的每一个原子dsl(1≤l≤ks) 也是逐一尺度，逐一位置进行的。在尺度s下，选出所有使用到第l个原子的子图像块：

其中，[s,p表]示位于“根”图像块Xc尺度为s、位置为p的子图像块；z(s,l,p)是对应子图像块其系数矩阵的第l行。

对于每一个子图像块[s,p]∈wsl，重新计算残差，此时参与计算的是字典中非dsl的其他原子：

其中，Tsp表示二元矩阵用以从“根”图像块中提出子图像块[s,p。]以wsl中所有子图像块的残差elsp为列向量，就构成矩阵对Esl进行SVD 分解，即：

用矩阵U的第一列更新字典原子，用矩阵V的第一列乘以Δ(1,1)来更新系数向量z(s,l,p)中集合wsl对应的元素。得到全局多尺度字典Dc即得到成对的多尺度HR 字典DH和LR 字典DL。重建阶段，给出LR图像Y的图像块y，需要通过LR字典DL得到它的稀疏系数α：

其中，λ为均衡系数，以权衡稀疏近似误差和非零项个数的比重。同样地，采用OMP 算法来求解此稀疏表示最优化问题。

得到LR图像块的稀疏系数α之后，HR图像X的图像块x就可表示为x=DHα，从而重建出HR图像块，将所有的HR图像块拼接后即可输出最终HR图像。

2 实验结果

分别采用仿真数据和真实数据对所提算法进行实验验证，同时从视觉和量化两方面评价实验结果。

2.1 训练数据

由于肺4D-CT 数据在轴向是低分辨率的，导致无法获取冠矢状面的HR图像。由此，通过实验对冠矢状面图像同横断面图像之间自相似性进行定性及定量的分析，验证其有效性。基于此相似性，采用横断面HR和LR图像块作为训练集，来联合训练HR和LR字典。

按照图像退化模型式（13）对真实的HR 图像进行降质处理，得到与之对应的LR图像：

其中，gk表示第k幅LR 观测图像，F表示原始HR 图像，Mk表示运动变形矩阵，Bk表示模糊矩阵，D表示降采样矩阵，nk表示加性噪声。

首先进行降采样，其系数为2；其次，通过叠加肺部的运动变形场来模拟图像变形；最后采用高斯函数使图像模糊。图5显示了一组横断面的HR 和LR图像。将所有HR和LR图像分块后，每个HR图像块和与其对应的LR 图像块组对，构成图像块对Pair={XH,YL}，以此作为训练集，为下一步字典训练奠定基础。

2.2 多尺度字典

图5 横断面HR和LR图像举例Fig.5 Example of high-resolution and low-resolution transverse images

图6显示了一组3 个尺度下（S=3）的全局HR 字典DH={Dh0,D1h,D2h}。该全局字典DH由3 个尺度下的字典构成，分别是：图6a 中s=0 时，字典Dh0；图6b 中s=1时，字典Dh1；图6c中s=2时，字典Dh2。实验中，设定每个尺度下的原子个数均为256。与图像自相似性验证实验中图像块的尺寸一致，这里设定“根”图像块的大小为16×16，子图像块的大小分别是8×8和4×4。因此，字典Dh0中每个原子维数n0=256，字典Dh1中每个原子维数n1=64，字典Dh2中每个原子维数n2=16。特别说明的是，联合训练的方式致使与全局HR 字典DH一同得到的还有LR 字典DL，其组成结构与DH相同。

2.3 仿真实验

本节同样采用横断面图像作为仿真数据，从视觉和量化评价两方面对实验结果进行比较。仿真数据的构造与2.1节中的方式相一致，此处不再赘述。

2.3.1 视觉评价 图7给出不同算法下横断面图像的重建结果图。左侧第1列显示的是真实HR图像。第2、3、4列给出基于单一尺度稀疏表示的SR算法重建结果，其图像块大小依次为4×4、8×8、16×16。本章提出基于多尺度的算法结果显示在第5列，实验中尺度个数设定为3，“根”图像块的大小为16×16，子图像块依照四叉树原则依次为8×8和4×4。各图中的红色方框区域图像均被放大后放置在其下方，以便加强对比。得益于多尺度的分析及处理，本章提出的算法与单一尺度算法相比，可以有效地捕获肺部不同尺度下的解剖结构特征，从而得到细节信息更为丰富的HR图像。

图8给出本章算法与双线性插值算法及POCS算法的横断面重建结果对比图。同样左侧第1 列显示的是真实HR图像。双线性插值算法和POCS算法的重建结果分别显示在第2、3 列。第4 列展示的是本章算法结果。将各图中的红色方框区域图像放大后置于第2行便于直观比较。对比双线性插值算法，本章算法重建出的HR 图像清晰度显著提升；对比POCS算法，本章算法不仅重建得到边缘有所增强的HR 图像，更避免了POCS 算法中对结果速度及精度造成限制的图像配准步骤。

图6 3个尺度下的全局HR字典DH= {Dh0,D1h,Dh2}Fig.6 Learned 3-scale global high-resolution dictionaryDH= {D0h,D1h,Dh2}

图7 不同算法下横断面图像的重建结果图Fig.7 Reconstruction results obtained by different algorithms

图8 本章算法与双线性插值算法及POCS算法的横断面重建结果对比图Fig.8 Transverse views of reconstructed images for comparison of the proposed approach with bilinear interpolation and POCS algorithm

2.3.2 量化评价 利用均方根误差（RMSE）对仿真数据结果进行量化评价。RMSE 值表征两组数据之间的离散程度，可以衡量真实图像和重建图像之间的偏差，其值越小代表两幅图像越接近。用公式表示如下：

其中，I表示真实图像，I表示重建图像。

根据式（14），分别计算5组数据对不同分块大小下单一尺度稀疏表示算法、双线性插值算法、POCS算法和本章算法重建结果的RMSE值，结果如表1所示。双线性插值算法所得的RMSE 值最高。虽然基于单一尺度稀疏表示的算法分别采用了与多尺度算法中“根”图像块及子图像块一致的分块大小，但是单一的处理方式使得大块中较小结构无法细化，小块与其所在的局部较大结构也无法保持良好的一致连续性，致使重建效果不佳。而与之相反的多尺度分析，不仅可以把握图像不同尺度下的结构特征，同时还是一个由大到小、由粗到精的优化处理过程。因此，它所重建出图像的RMSE值更低，也更为准确。本章算法尽管与POCS 算法重建结果的RMSE 值相差并不显著，但是本章算法有效避免了运动估计的过程。

2.4 多平面重建结果

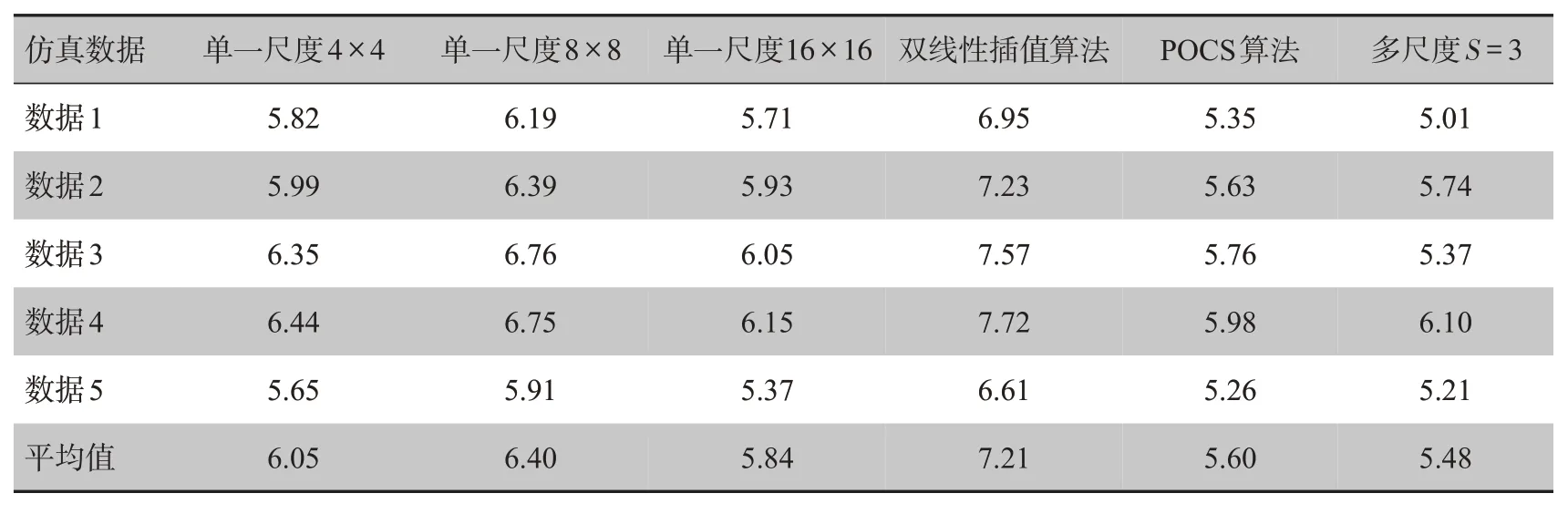
表1 不同分块大小下单一尺度稀疏表示算法、双线性插值算法、POCS算法和本章算法重建图像的RMSE值比较结果Tab.1 Comparison of root mean square errors among single-scale sparse representation with different patch sizes,bilinear interpolation,POCS algorithm and the proposed approach

图9给出单一尺度算法和本章算法下冠矢状面图像重建结果。第1、2、3 列是不同分块大小（4×4、8×8、16×16）下单一尺度稀疏表示算法的重建结果。本章算法的结果显示在第4 列。为了更加直观地对比，各图中的红色方框区域图像均被放大后放置在其下方。与基于单一尺度的算法相比，本章算法在捕获肺4D-CT 数据不同尺度的解剖信息方面更有效，重建出视觉效果更好的HR图像。

图10显示双线性插值算法、POCS算法和本章算法下冠矢状面图像重建结果。第1、2 列分别是双线性插值算法和POCS 算法的重建结果。第3 列是本章算法的重建结果。各图中的红色方框区域图像均被放大后放置在其下方，以便于比较。对比双线性插值算法，本章算法重建出的HR图像清晰度显著提升；较于POCS算法，本章算法能够改善HR图像细微结构的显示质量。

3 讨论

基于模型方法需要采用配准或块匹配方法进行运动估计，这导致重建速度和精度往往受到配准速度和精度的制约。而基于学习的SR重建方法可以避免这一过程。因此，本研究提出一种基于图像自相似性的多尺度稀疏表示肺4D-CT图像超分辨重建方法。通过验证冠矢状面图像和横断面图像中不同尺度下组织结构的自相似性，利用横断面图像来代替冠矢状面图像，将对应的HR和LR图像块两两组对，作为训练集。其次，面对肺4D-CT 图像解剖结构特征存在于不同尺度之下的数据特点，引入多尺度策略，根据四叉树原理将“根”图像块划分为各个尺度的子图像块，并建立全局多尺度字典。本研究提出的算法不仅有效地解决了在缺失原始HR 图像情形下构建训练集的难题，还通过多尺度分析的手段同时捕获了肺部不同尺度下的解剖结构特征。

虽然笔者通过实验从定量和定性两方面均对冠矢状面图像同横断面图像之间的自相似性进行验证，但是重建结果显示还是存在一定的干扰，接下来将引入金字塔模型［19］，直接由输入图像本身生成训练集，来对提出的算法进行进一步改善。另外，还将进一步研究如何使该算法能够用于放大倍数更大的图像重建，以满足临床对于图像质量及图像放大的双重需求。

图9 单一尺度算法和本章算法下冠矢状面图像重建结果Fig.9 Coronal and sagittal views of image reconstructed with single-scale approach and the proposed approach

图10 双线性插值算法、POCS算法和本章算法下冠矢状面图像重建结果Fig.10 Coronal and sagittal views of images reconstructed with bilinear interpolation,POCS algorithm and the proposed approach

总的来说，本研究提出的算法不仅能够重建出细节信息更为丰富清晰的HR图像，还能避免对结果速度及精度产生影响的运动估计，同时也可为4D心脏图像、4D超声图像的SR重建提供新思路。