基于Radau伪谱法的复合电源电动汽车能量管理策略优化*

刘延伟，朱云学，林子越，赵克刚，叶 杰

（1.广东工业大学机电工程学院，广州 510006； 2.华南理工大学机械与汽车工程学院，广州 510641）

前言

传统燃油汽车在给人类生活带来方便、舒适的同时，给全球能源与环境带来了严峻的挑战，而电动汽车可大大减少车辆对化石能源的消耗，还具有零排放、噪声小等优点，可缓解传统燃油车面临的能源与环境问题。电动汽车需要一个高能量密度与高功率密度的电能存储系统来保证车辆的续驶里程和动力性能。电池具有高能量密度，但其功率密度较低，寿命相对较短；超级电容的功率密度很高，且其使用寿命很长，但其能量密度较低。电动汽车电池-电容复合电源系统（hybrid energy storage system，HESS）可充分利用两者的优点，提高车辆的能量利用率和动力性，延长车辆的续航里程。

复合电源的能量管理策略对电动汽车的经济性、动力性和电池寿命等有重要影响，且电池与超级电容的动力学特性及工作模式具有很大差别，故对两者进行有效的能量管理十分重要，国内外学者对此进行了较为广泛的研究。如利用NSGA-II多目标算法对复合电源电动汽车的参数匹配与能量管理策略进行优化［1-2］；有采用凸优化对复合电源进行参数匹配同优化能量管理策略［3-4］；有些文献中采用模型预测控制［5-6］、基于规则控制策略、动态规划算法［7-9］、模糊逻辑控制［10］对复合电源能量管理策略进行优化；上述文献中，较少在仿真过程中将电池充放电时的内阻特性考虑在内，导致优化结果并不符合真实情况，且在电池寿命模型中没有加入为避免电池大电流放电的惩罚因子，造成电池大电流放电而缩短使用寿命；而遗传算法收敛速度慢，且容易陷入局部最优；凸优化在应用时需对优化问题进行凸化处理，对于实际问题的应用比较困难；动态规划算法计算复杂程度高，且求解的精度严重依赖于网络格点的密度；模型预测法与基于规则控制策略可在线应用，但其准确度都具有很大的敏感性；模糊逻辑控制的实时性较强，但无法保证全局最优。

复合电源能量管理优化具有强非线性、多模式等特点，相较于现阶段的复合电源能量管理优化方法，伪谱法作为一种全局优化法具有收敛速度快、收敛半径大、初值敏感性低、求解精度高等优点，且其优化结果一定是全局最优［11-12］。如利用Legendre伪谱法对无动力中断两挡变速器的换挡过程进行了轨迹优化［13］；利用Legendre伪谱法对无级变速器车辆经济性续航策略进行优化，提升了汽车的节油能力［14］；利用Gauss伪谱法得到了4挡机械式自动变速器电动汽车的最优换挡策略［15］；还有利用Radau伪谱法对串联式履带车辆的能量管理策略进行优化［16］。

本文中以半主动式电池端负载构型的复合电源电动汽车为研究对象，考虑电池充放电时的内阻特性，以加入惩罚因子的电池寿命模型为目标函数，以整车性能、电池与电容的相关参数为约束，运用Radau伪谱法对复合电源电动汽车的能量管理策略进行优化。

1 复合电源模型

1.1 复合电源拓扑图

复合电源系统有被动式、半主动式与全主动式3种构型。被动式复合电源特点是电池与超级电容都直接并联在直流电母线上，其结构简单，成本低廉，但工作中电流不可控；全主动式构型的特点是采用两个DC／DC变换器，结构和控制过于复杂，配置成本高；半主动式结构中电池组或超级电容组通过DC／DC变换器与母线连接，电流可以由DC／DC变换器控制，复合电源灵活性得到保证。以超级电容端连接负载时，直流高压母线直接与超级电容相连，电压范围波动大，难以控制；以电池组端连接负载时，系统更易于控制并且总线电压更加稳定，同时降低了系统成本。故本文中采用半主动式复合电源-电池端负载构型进行研究，拓扑结构如图1所示。

图1 半主动式复合电源-电池端负载构型

1.2 电池模型

电池单体模型采用如图2所示的内阻模型。

图2 动力电池单体的等效模型

图中：ub为电池开路电压；ub0为电池路端电压；ib为电池电流（放电为正，充电为负）；Rb为电池的等效串联内阻。电池荷电状态（battery state of charge，BSOC）采用安时积分法进行计算。

式中：BSOC（t0）为电池初始荷电状态的值；Qb为电池容量。开路电压ub与荷电状态BSOC呈非线性的关系［3］，如图3所示，其内阻Rb的值与其充、放电状态有关［17］，如图4所示。

图3 电池开路电压与BSOC的关系

图4 电池充、放电电阻与BSOC的关系

1.3 超级电容模型

超级电容的单体模型如图5所示。

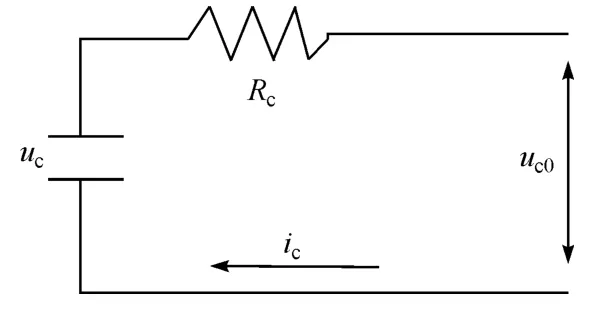
图5 超级电容单体的等效电路模型

图中：uc为超级电容的开路电压；uc0为超级电容的路端电压；ic为超级电容电流（放电为正，充电为负）；Rc为超级电容的等效串联内阻。超级电容荷电状态（ultracapacitor state of charge，USOC）采用如下方法进行计算。

式中：USOC（t0）为超级电容初始荷电状态的值；Cc为超级电容的容量；ucmax为超级电容最大电压。

1.4 DC／DC模型

由于电池组和超级电容充放电特性不同，两者直接并联会出现电压不匹配（电压钳制）等问题，使得复合电源系统的优势下降。本文中选用双向DC／DC变换器，其作用是控制传递功率、调控电压大小。而能量在经过DC／DC变换器的传递过程中会出现损失，因此在复合电源系统中必须考虑其效率的影响。

1.5 母线功率平衡模型

整车的需求功率为

需求功率与直流母线的功率平衡为

直流母线与能量源之间的功率平衡为

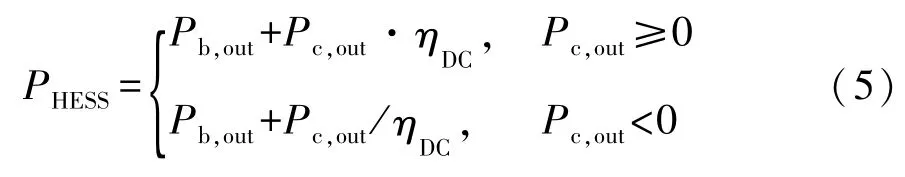
式中：Pd为整车需求功率；PHESS为复合电源功率；Pb，out为电池功率（放电为正，充电为负）；Pc，out为超级电容功率（放电为正，充电为负）；v为车速；m为电动汽车质量；g为重力加速度；f为滚动阻力系数；α为道路坡度，本文中取α=0；CD为空气阻力系数；A为迎风面积；δ为汽车旋转质量换算系数；ηt为传动系统效率；ηDC为DC／DC变换器的效率；ηe为电机效率；ηreg为制动能量回收效率。

2 初步参数匹配

在确定复合电源系统构型后，需对系统中电池组与超级电容进行初步匹配，使得复合电源能够满足车辆的能量需求与功率需求。

2.1 电池参数

复合电源系统中采用的电机参数如表1所示［17］。

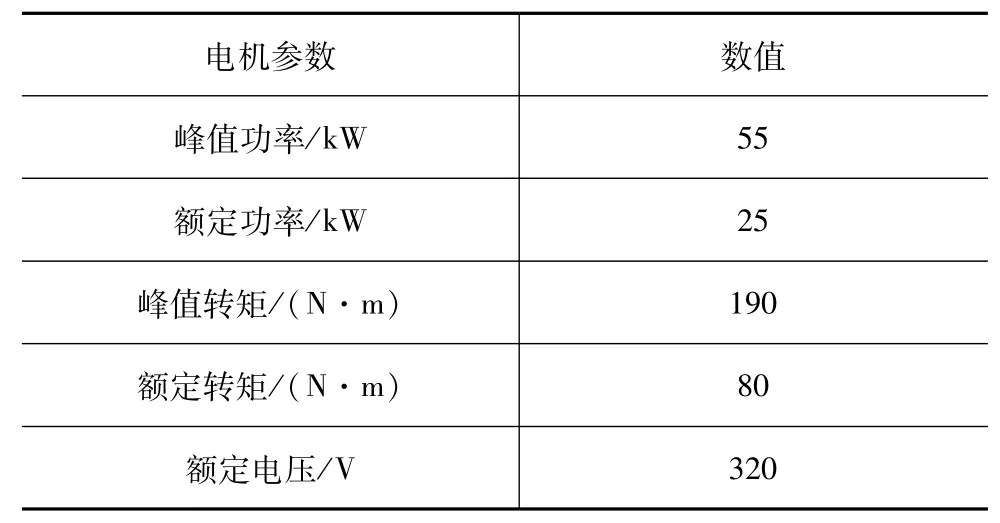
表1 车载永磁同步电机参数

电池单体串联数目为

式中：nbs为电池组单体串联数目；ub_cell为电池单体电压；ue_nom为电机额定电压。对电池单体串联数取整为nbs=90。由电动车最大续航里程150 km（速度为60 km／h），可得

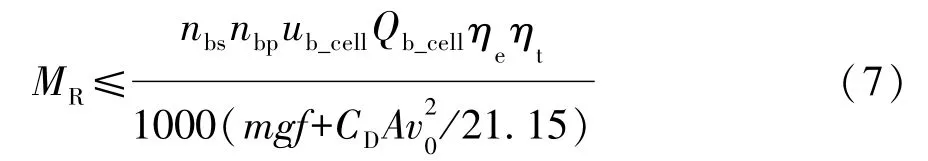
式中：MR为最大续航里程；nbp为电池组单体并联数；v0为最大续航里程下的速。对电池单体并联数取整为nbp=13，故采用13组串联数为90电池模块进行并联，在仿真过程中电池组初始BSOC设定为0.7。

2.2 超级电容参数

由于DC／DC变换器的效率与两端电压比值相关，当其比值接近1时效率较高，故选取超级电容组端电压小于并接近于电池组的电压，即

式中：uc_cell为超级电容单体开路电压；ncs为超级电容组单体串联数目，取为100。车辆等速行驶时平均功率为

式中：v为行驶速度，取为60 km／h。超级电容应满足电池组平均功率之外的需求功率，且应满足tp=10 s峰值助力需求，则其并联数按式（10）计算。

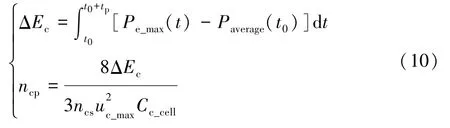
式中：ΔEc为超级电容能量需求；Pe_max为电机峰值功率；ncp为超级电容并联数；uc_max为超级电容单体电压上限；Cc_cell为超级电容单体容量。根据式（10）求出ncp≈1，故超级电容组由100个超级电容单体直接串联而成，在仿真过程中超级电容初始USOC设定为0.7。

3 伪谱法优化步骤

本文中选取BSOC和USOC为优化过程中的状态变量，Pb，out为优化过程中的控制变量。电池的功率按式（11）计算。

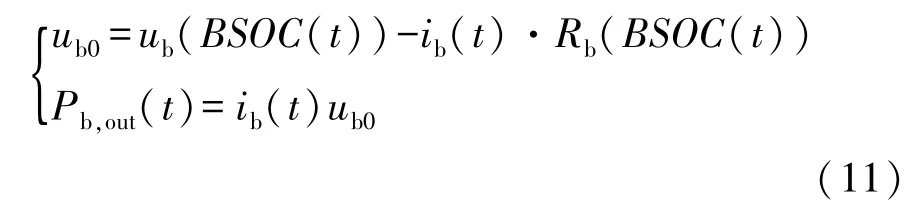
联立式（1）和式（11），电池荷电状态BSOC对时间的1阶微分可表示为

由于超级电容的开路电压uc与其荷电状态USOC呈线性关系，则超级电容的能量Ec按式（14）计算。

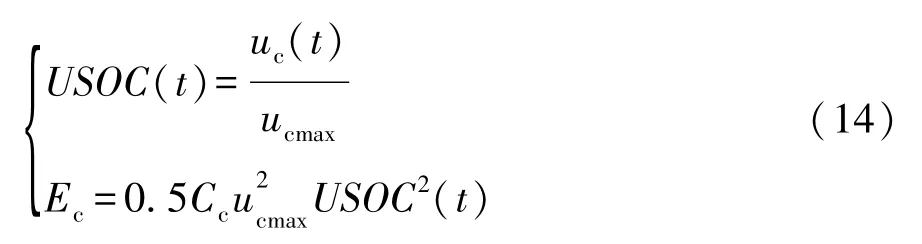
联立式（2）、式（5）、式（13）和式（14）可得，超级电容荷电状态USOC对时间的1阶微分如式（15）所示，式中sign为符号函数。

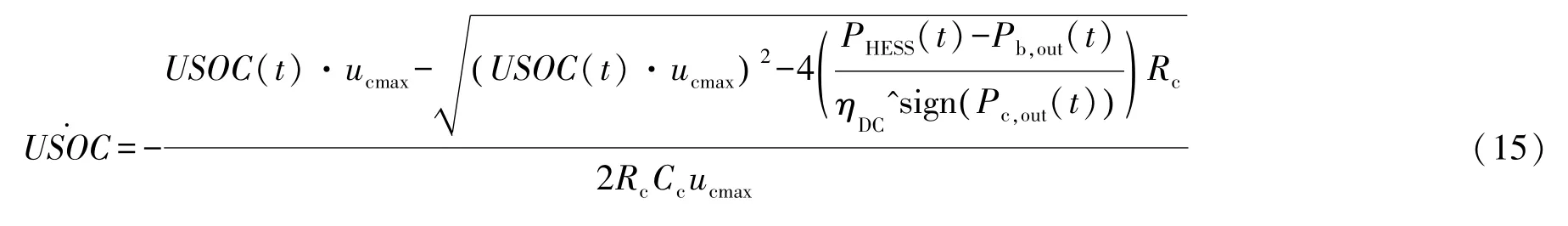
Radau伪谱法将状态变量和控制变量分别离散后，利用Lagrange插值多项式逼近状态和控制变量，将状态方程的微分运算和性能函数中的积分运算均转化为代数运算，最终将最优控制问题（OCP）转化为以节点处的状态变量、配点处的控制变量为待优化参量的非线性规划问题（NLP），具体步骤如下。

将复合电源电动汽车在NEDC工况下行驶分为Q个阶段，其初始时间点及Q-1个分段点分别记为T0，T1，…，TQ，且T0＜T1＜…＜TQ。

（1）时域的变换，将整个时域中的每个时间段［Tq-1，Tq］（其中q∈[ 1，Q] ∩Z＋）转换到区间［-1，1］，使其满足Legendre正交多项式的定义区间。

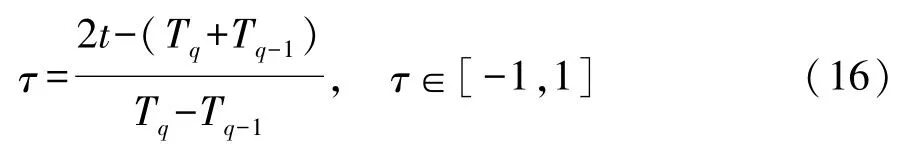
（2）配点与离散化，Radau伪谱法的配点为LGR点，即取值区间为τ∈（-1，1］或τ∈［-1，1），本文中选取τ∈（-1，1］作为配点区间，其为多项式PN（τ）-PN-1（τ）的根，PN（τ）为N阶Legendre正交多项式，即

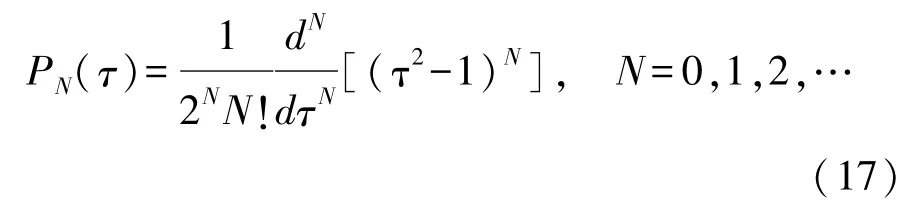
Radau伪谱法的节点为N个LGR配点加初始时间点τ0=-1，故其节点数为N＋1。对于含Q个阶段的伪谱拼接法，每个阶段内的节点数可以不同，记为Nq＋1，并将第q个阶段内的节点记为 τq，i，其中i=0，1，…，Nq。将电池荷电状态（BSOC）与超级电容的荷电状态（USOC）作为仿真过程中的状态变量，在节点处将其离散化，每个阶段内的状态变量可表示为

则每个阶段下状态变量的时间历程曲线可通过Nq＋1个Lagrange插值多项式来逼近。

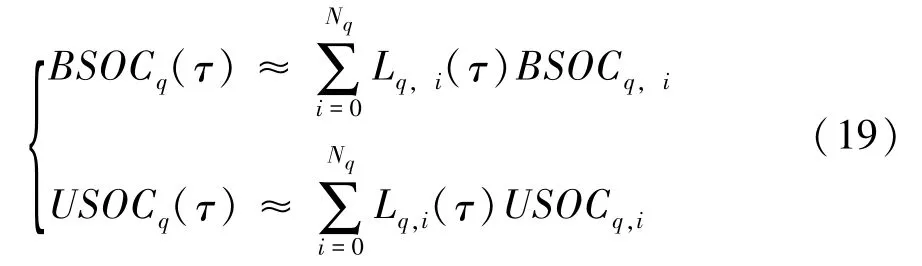
式中Li（τ）为Nq次Lagrange插值基函数。

将电池功率Pb，out作为优化过程中的控制变量，只在配点处将其离散化，每个阶段内控制变量可表示为

则每个阶段下控制变量的时间历程曲线可通过Nq个Lagrange插值多项式来逼近。

（3）状态方程转化为代数约束，经过配点与离散化后，状态变量由全局插值多项式逼近，因此其微分可通过对式（19）插值多项式求导来表示，即

式中：τq，k为第q阶段的配点，其中为Nq·（Nq＋1）的微分矩阵，表示第q阶段的Lagrange插值基函数在各配点处的微分值，可由式（25）得出。

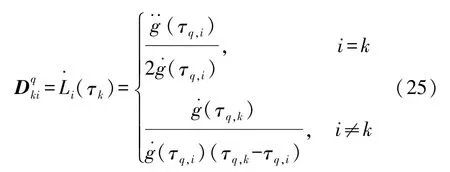
式中：g（τq，i）=（1＋τq，i）［PNq（τq，i）-PNq-1（τq，i）］。结合式（12）、式（15）、式（24）和式（25）则复合电源汽车能量管理最优控制问题在第q阶段的动力学方程约束转化成在配点τq，k处的代数约束：

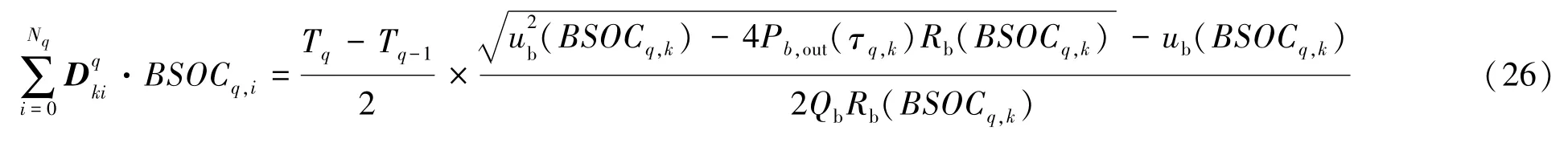
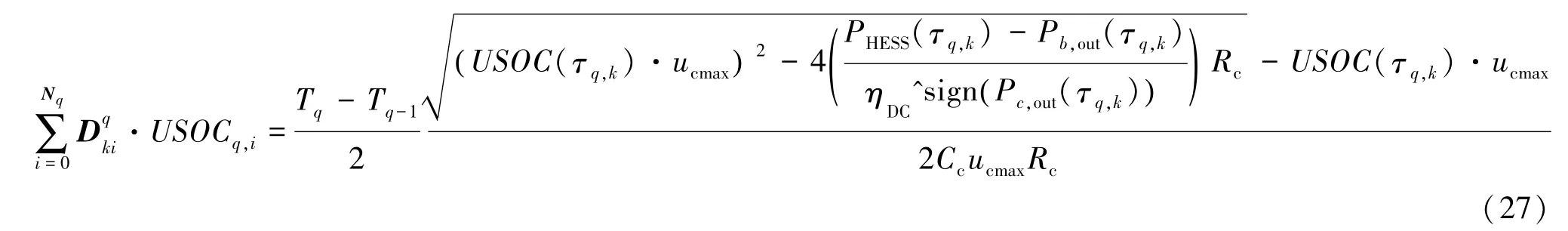
（4）性能函数的转化，在复合电源汽车的能量管理最优控制问题中，性能指标由电池的安时流通组成，其中为避免电池大电流放电，在目标函数中加入惩罚因子［18］，如式（28）所示。

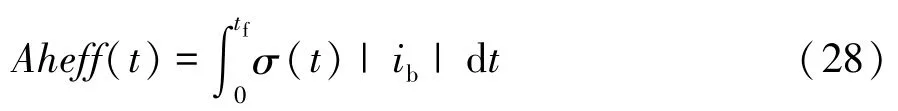
式中σ为惩罚因子，其主要决定因素取决于充放电倍率kb、温度和放电深度。

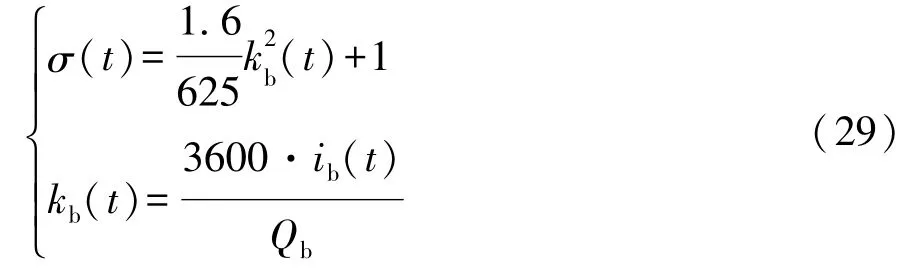
式中：ib为充放电电流；Qb为电池额定容量。性能函数中仅含有积分项（Lagrange型性能指标），可通过Gauss-Radau积分方法近似为

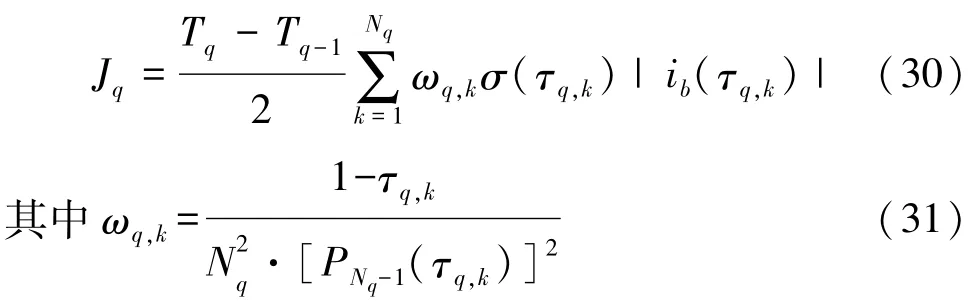
式中 ωq，k为积分权重。

（5）OCP问题转化为NLP问题，通过以上步骤，原复合电源能量管理最优控制问题可转化为待优化变量的NLP问题，即

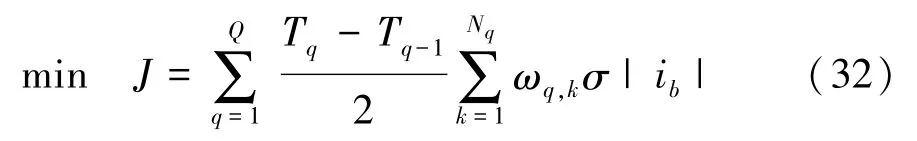
状态方程如式（26）和式（27）所示，其中的约束条件为

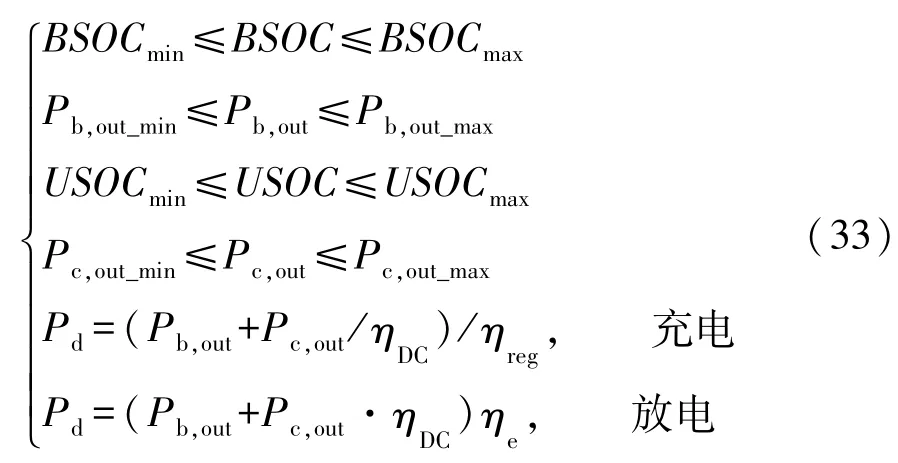
该NLP问题的待优化变量为LGR点处的电池组荷电状态BSOC、超级电容组荷电状态USOC和电池输出功率Pb，out，可通过成熟的高维稀疏NLP求解器SNOPT进行求解，其核心是基于线搜索且具有局部超线性收敛性的序列二次规划法。

4 参数设置及结果分析

4.1 优化参数设置

优化过程中的参数如表2所示，电池型号为Panasonic NCR 18650B，超级电容型号为Maxwell BCAP3000，仿真参数参照文献［3］和文献［17］。

表2 仿真参数

本文中选用NEDC循环工况进行仿真优化，工况与整车需求功率如图6和图7所示。根据汽车需求功率的不同，将汽车的行驶工况分为功率上升阶段（加速工况）、功率维持阶段（匀速工况）、功率为负阶段（减速工况）和功率为零4种情况。在复合电源电动汽车中，加速工况由电池与电容共同提供能量；匀速工况由电池提供能量；减速工况仅由电容回收制动产生的能量，当其荷电状态达到上限后不再回收能量；功率为零工况两者均不工作。由于整个NEDC工况阶段较为复杂，划分的阶段数较多（共69个阶段），本文中仅以城郊工况为例，根据伪谱法划分阶段的原则，将城郊工况共分为12个阶段，如表3所示。

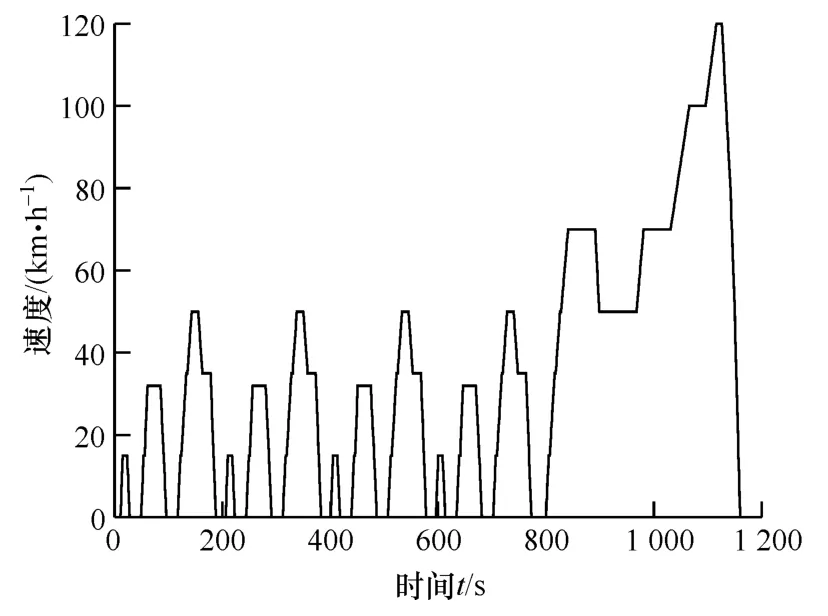
图6 NEDC循环工况

图7 NEDC工况整车需求功率

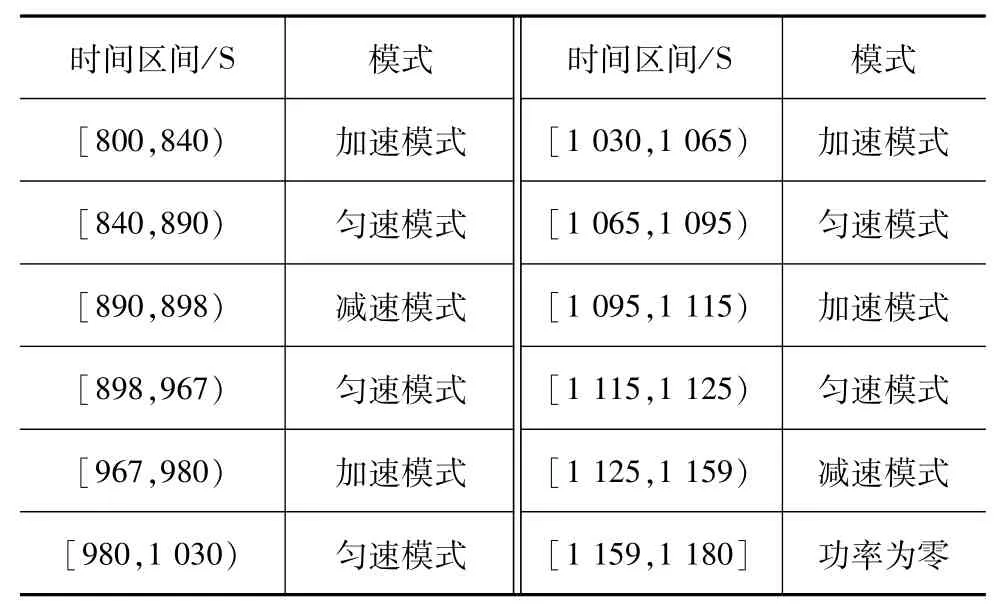
表3 NEDC城郊工况阶段划分情况

4.2 优化结果及分析

单一电池组BSOC计算结果如图8所示，电流计算结果如图9所示，功率计算结果如图10所示。经过Radau伪谱法优化计算，复合电源SOC优化结果如图11所示，电流优化结果如图12所示，功率优化结果如图13所示，超级电容功率、电池组与需求功率的关系如图14和图15所示。以下在对单一电池组计算结果和复合电源优化结果说明的基础上，进一步进行对比分析。

图8 NEDC工况单一电池BSOC计算结果

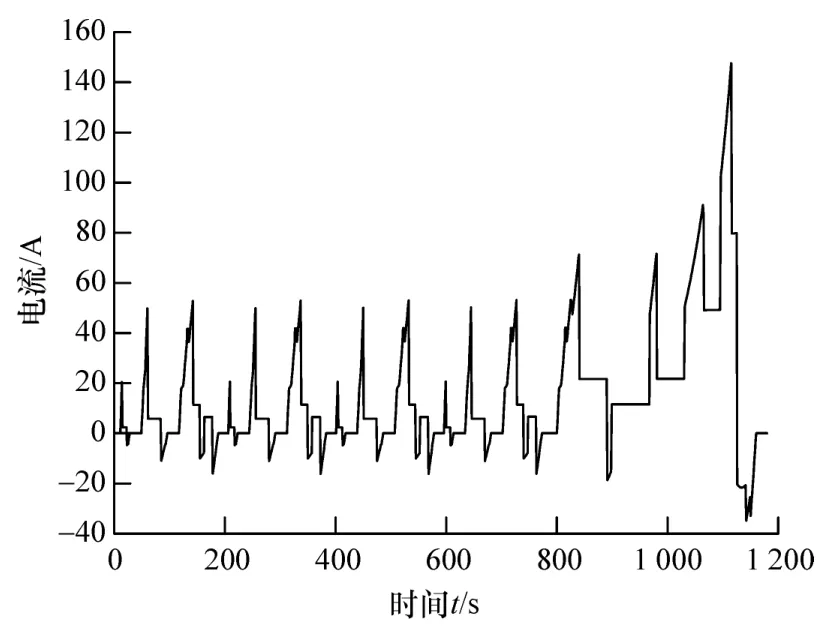
图9 NEDC工况单一电池电流计算结果

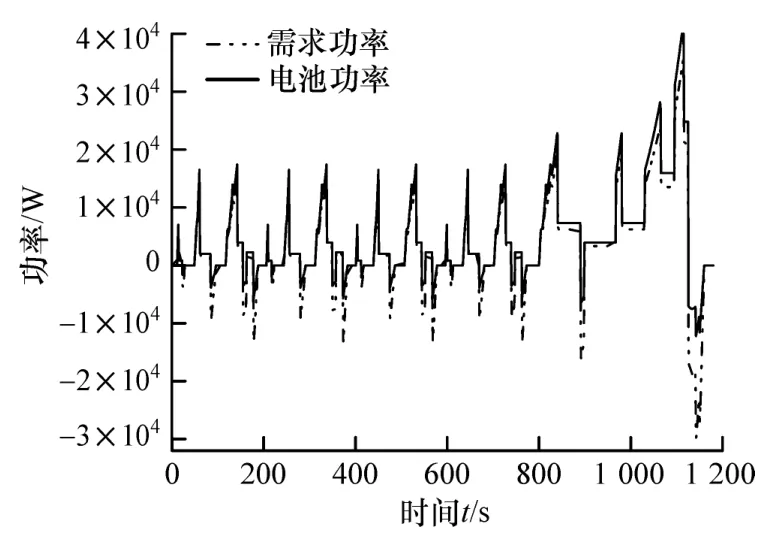
图10 NEDC工况单一电池功率计算结果

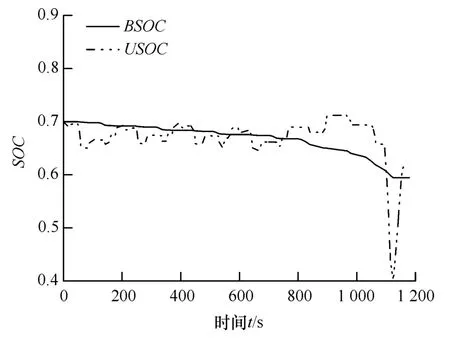
图11 NEDC工况复合电源SOC优化结果

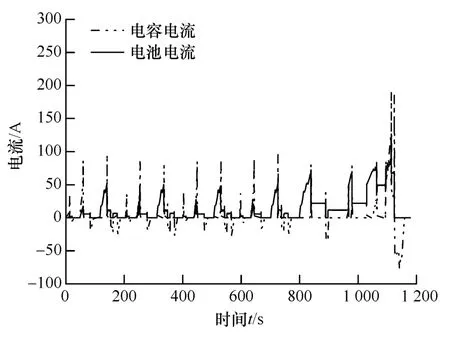
图12 NEDC工况复合电源电流优化结果

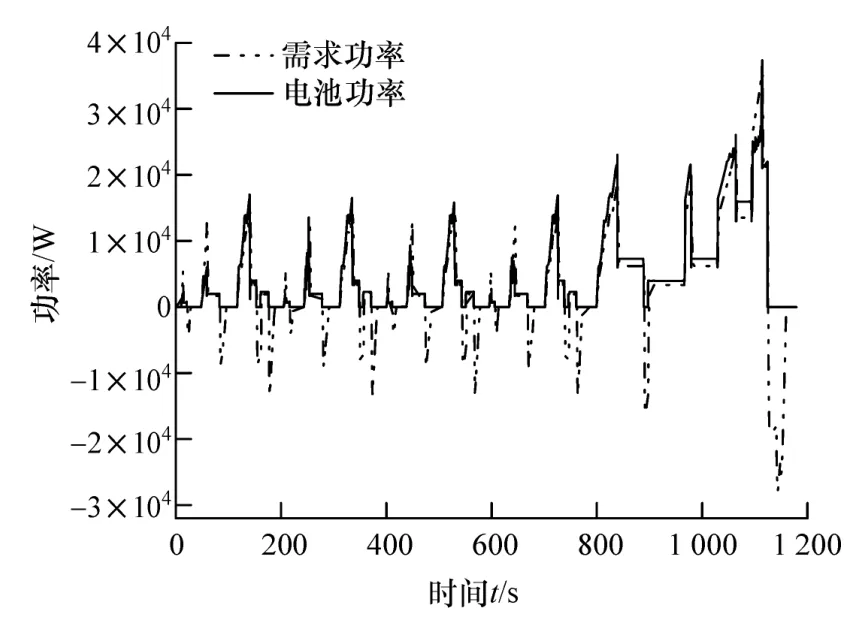
图13 NEDC工况复合电源功率优化结果

图8为单一电池组供电BSOC的变化曲线，电池必须应对所有的充、放电阶段，BSOC既有下降阶段也有上升阶段，其终值为0.592 3。图11为复合电源供电状态变量SOC的变化曲线，电池仅应对放电阶段，BSOC只下降，最终稳定在0.594 5，在0-1 095 s内，USOC在0.67上下波动，而在1 095-1 125 s时，USOC下降到其最低值0.4，最终稳定在0.614 5。对比图8和图11可知，单一电池组供电BSOC的波动幅度明显，且其终值小于复合电源中BSOC的终值，由于超级电容加入复合电源中BSOC的下降幅度较缓，且充电阶段的电量全由超级电容吸收，在最后的加速阶段，超级电容耗光所有电量，表明充分利用了超级电容的容量。

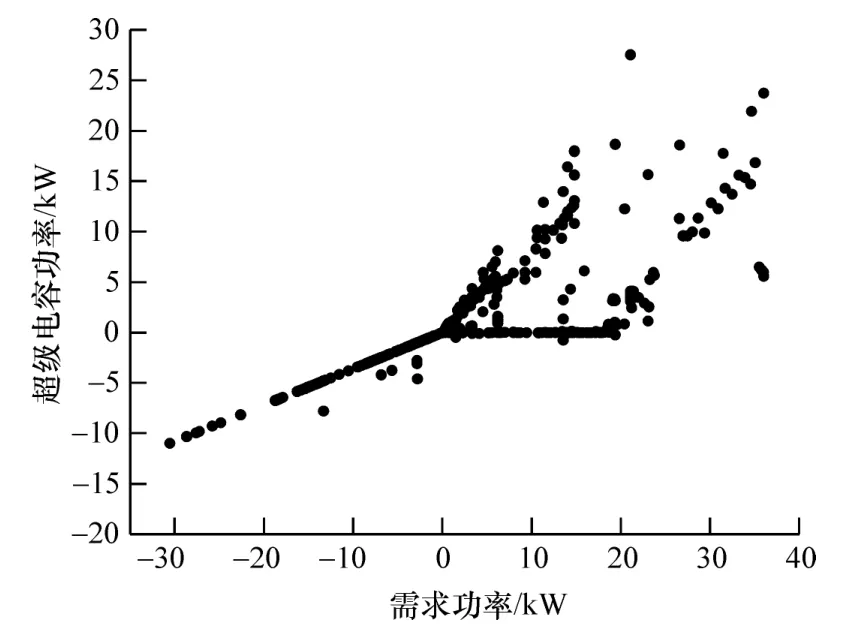
图14 超级电容功率与需求功率的关系

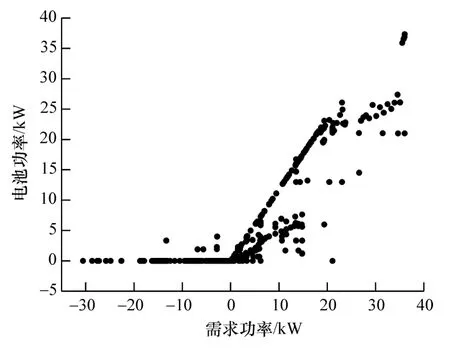
图15 电池功率与需求功率的关系

图9为单一电池组供电电流变化曲线，其电流范围为-34.76～147.7 A，电池组电流波动范围较大，对电池组造成不可逆的损伤；图12为复合电源供电电流变化曲线，其电流范围为0～126.7A，电池组电流波动范围减小。对比图9和图12可知，超级电容的加入防止了电池组过充、过放，缓解了电池组的工作压力，延长了电池组的使用寿命。

图10为单一电池组供电功率变化曲线，由于系统效率的原因，电池组功率在加速阶段、匀速阶段略大于需求功率，而在减速阶段吸收部分需求功率；图13为复合电源供电电池功率变化曲线，在加速阶段超级电容应对部分功率，减小电池组的功率输出，匀速阶段仅由电池组提供电能，在减速阶段需求功率都由超级电容回收。对比图10和图13可知，经过伪谱法优化后的复合电源能量管理策略能够在满足整车需求功率的同时减小电池组的功率输出，即超级电容起到了削峰填谷的作用。

图14和图15更为直观地显示了复合电源中超级电容功率与需求功率、电池组功率与需求功率的关系。可以看出，在减速阶段需求功率为负时，功率都由超级电容吸收，且电池为超级电容提供不超过5 kW的功率；在匀速阶段需求功率仅由电池组提供，其中匀速功率包括0.8，2，4，7.3，14和22 kW；需求功率为0-20 kW时的加速阶段分为两种，一种为较长时间的大需求功率阶段电池组功率与需求功率近似线性关系，超级电容补充剩余功率，另一种为较短时间的小需求功率阶段电池组提供不超过8 kW的功率，其余由超级电容补充，以上优化结果表明了超级电容快速充放电的特性；在需求功率超过20 kW时，超级电容与需求功率呈线性关系，此时电池组补充剩余功率；由于伪谱法将工况分为多阶段，在由加速阶段变为其他阶段时，电池组功率发生突变导致超级电容进行功率补充；在超级电容耗完电量后，需求功率由电池组单独承担。

本文中通过电池等效寿命来比较复合电源系统与单一电源的优劣，其中电池等效寿命计算公式［18］为

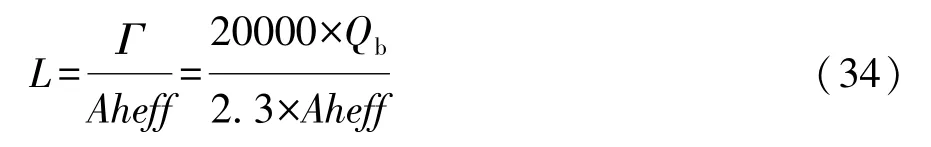
式中：Γ为电池的总安时流通量，其值只与电池自身因素相关，且是一个常数，当Γ=Aheff时，电池达到寿命极限；L为等效电池寿命，本文中表示电池组在NEDC工况下可循环行驶的次数。最终得复合电源系统中电池组可循环行驶的次数为82 150，而单一能量源中电池组可循环行驶的次数为65 399，在加入超级电容的复合电源系统中，提高了电池组可循环行驶的次数。

5 结论

本文中以加入惩罚因子的电池寿命模型为目标函数，考虑了电池充放电时的内阻特性，利用Radau伪谱法对复合电源电动汽车的能量管理策略进行优化。

对比单一电池组供电，Radau伪谱法优化后的HESS减小了电池组的安时流通，缩小了电流、功率波动范围，且HESS中电池组功率与超级功率均与HESS功率出现了分段的线性关系，最优能量管理策略能充分利用两能量源的各自优势。

复合电源系统中电池组的等效寿命为82 150次，较单一电池组能量源中电池组的等效寿命提高了25.61%。基于Radau伪谱法的能量管理策略优化能进一步优化复合电源系统的工作状态，延长电池的使用寿命。本文中提出的理论为复合电源的能量管理策略提供了一种快速、稳定的优化方法，为匹配最优系统参数奠定了工作基础，还可作为其他优化策略的评估基准。