基于多模糊控制的电电混合汽车能量管理策略*

姚堤照，谢长君，曾 甜，黄 亮

（武汉理工大学自动化学院，武汉 430070）

前言

随着能源与环境问题日益严峻，国内外各大汽车厂商和研发机构加快对清洁能源汽车的研究。纯电动汽车以其结构简单、清洁环保等优势，在汽车领域得到大力推广。目前，阻碍电动汽车发展的两个重要因素是续航里程和电池循环寿命。针对这些不足，动力电池、超级电容和双向DC／DC变换器的复合能源系统被提出，超级电容具有循环寿命长、功率密度高等优点，与锂电池的高能量密度实现优势互补，对延长动力电池循环寿命，提高制动能量的回馈效率和整车续航里程具有重要意义［1-3］。

目前混合动力系统开发常见的能量管理策略分为3类：基于简化模型或逻辑规则的策略，基于模糊控制和预测控制等智能控制方法的策略，基于动态规划与极小值原理等动态优化方法的策略［4-7］。上述方法中基于模糊控制的智能方法以其适应性强、控制效果明显等优点被广泛使用。考虑单一的控制方式无法较好适应汽车复杂工况，多个控制器的组合调节多个参数可提高控制器的智能性，能够更好适应复杂系统。其中，文献［8］中提出了基于粒子群优化的模糊控制器，解决了动力系统能量分配问题，但仅能通过离线求解优化，不能在线更新隶属函数，难以应对复杂变化的运行工况；文献［9］中提出了自适应PI模糊控制，利用超级电容起到“削峰填谷”的作用，但控制过程严重依赖专家经验，不具有普适性；文献［10］中提出了基于优化模糊规则的功率分配因子控制算法，取得了较好的控制效果，但优化过程过于依赖专家经验，且单一模糊控制存在适应性问题。

多种控制方式的组合可提高控制器的适应性和稳定性，但也使控制策略变得更复杂。因此，组合控制的成员算法应具有结构简单、控制效果理想的特点。经分析，本文中提出了基于模糊方波调制的联合控制策略，以简单智能的算法实现了复合动力系统的能量高效分配。

1 系统拓扑结构与参数选定

电动车复合能源动力系统的拓扑结构种类繁多［11］，其中超级电容与双向DC／DC变换器串联后的结构与电池组并联，再连接到功率母线的拓扑结构，具有结构简单、控制方便的优点，被广泛应用到理论研究中。因此本文中采用该拓扑结构，如图1所示。

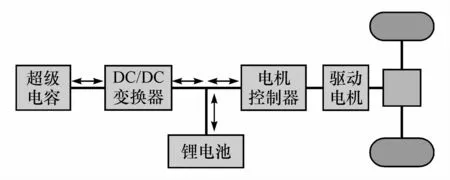
图1 动力系统拓扑结构

本文中以某小型电动汽车为原型，设计实验台架，整车参数设计如表1所示。

表1 整车参数

根据整车参数，可计算得到整车最大驱动功率为12.19 kW，电机最大转矩为58.2 N·m，电机最高转速为3 577.6 r／min。选择的驱动电机参数见表2。

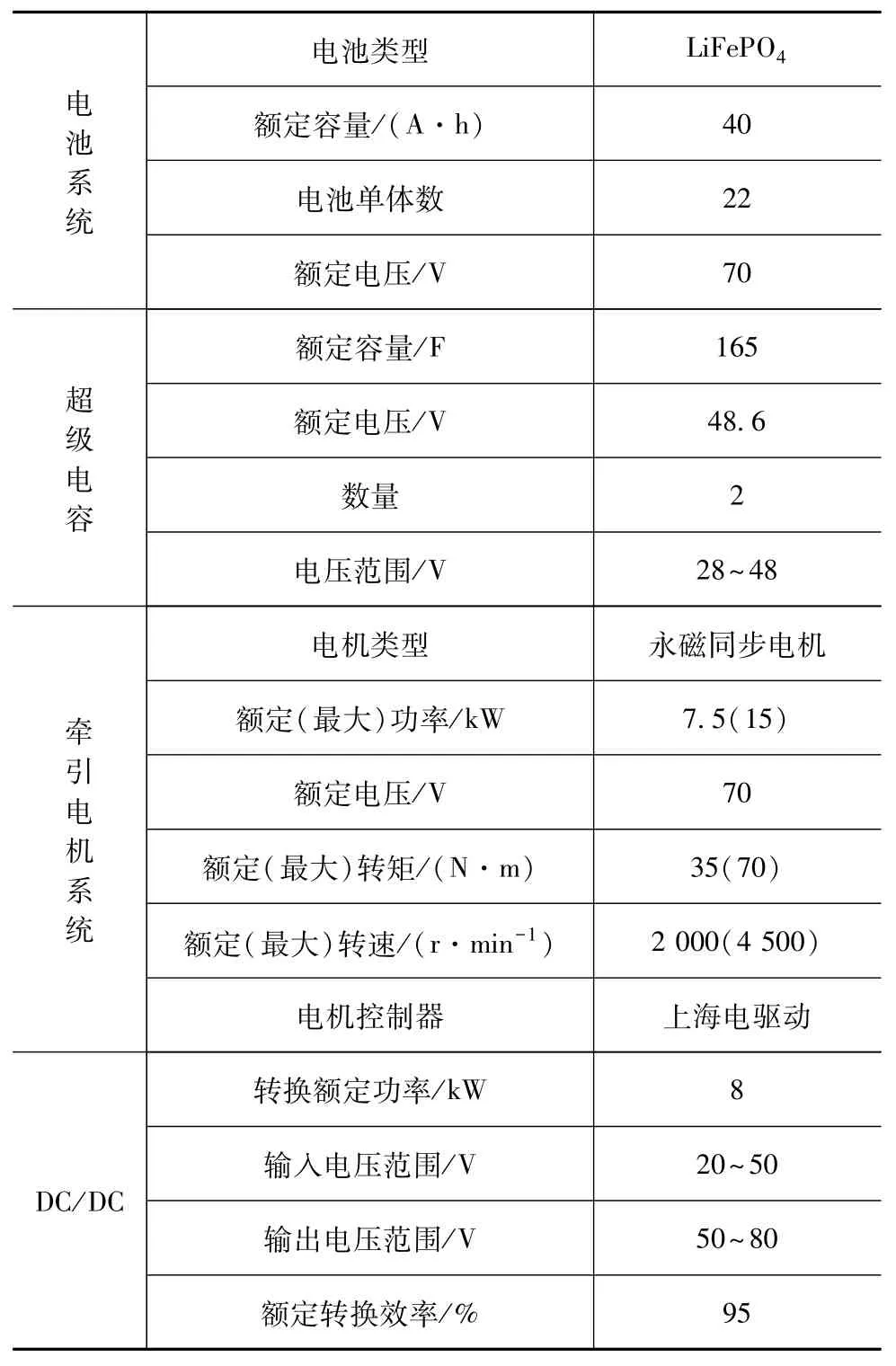
表2 实验台架参数表

根据电机额定电压和额定功率确定直流母线电压等级为70 V，电池组最大输出电流为107 A，因此选取中航锂电40 A·h磷酸锂铁作为动力电池，其标称电压为3.4 V，最大放电倍率为3C，由22块单体串联成组。超级电容模组由两组48.6 V／165 F商用Maxwell超级电容模块并联，再与8 kW双向DC／DC串联组成作为辅助能量源。台架具体参数设计见表2。

2 能量管理控制器设计

在复合能源动力系统中，主要通过双向DC／DC来调节超级电容输出功率，使锂电池工作在合适的输出范围内。一般来说，电池的充放电倍率与工作温度是影响电池寿命的两大因素，因此超级电容的调节原则可分为两类：（1）超级电容承担需求功率的高频部分；（2）超级电容抵消需求功率的高幅值部分。考虑到通信延时和双向DC／DC响应时间，超级电容承担需求功率的高频部分时存在控制实时性问题，因此本文中以超级电容承担需求功率的高幅值部分为调节原则，将锂电池放电倍率控制在1C以内（根据表2计算，锂电池组充放电功率≤2500 W，下面电流倍率将用电池输出功率来描述），减少在锂电池内阻上的损耗，延长电池组寿命。考虑到单一模糊控制器的适应性问题，本文中的研究采用基于功率分配因子模糊控制算法与简单的模糊方波调节控制算法联合，实现两种控制方法的优势互补，其具体结构如图2所示。

图2 基于模糊方波调制的联合控制器结构

2.1 模糊方波调节控制器设计

方波调节控制遵循“削峰填谷”的控制原则，可作以下设定：

当需求功率Pre＞0，设锂电池输出功率为一定值Pbat0，可得超级电容输出功率为

则锂电池输出功率可被调制成限幅方波，本文中称此为方波调节控制。然而，当系统频繁运行在Pre±Δ=Pbat0时（Δ为双向DC／DC允许启动功率），会造成超级电容输出功率Puc在充放电之间震荡，双向DC／DC过于频繁切换，缩短使用寿命。为解决此问题，本文中根据需求功率大小在一定范围内调节锂电池输出功率Pbat0，从而消除Puc在±Δ之间震荡。同时，为减少双向DC／DC的启动频率，根据本文中实验平台参数需做以下限制：

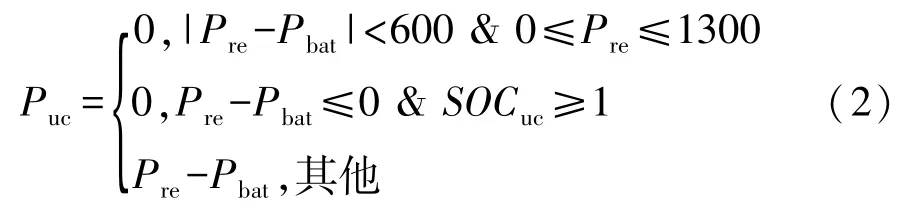
为实现Pbat0可在一定范围内合理变化，本文中选用模糊控制方式调节Pbat0，并称此为模糊方波调节控制器。选择关键参数需求功率Pre和超级电容SOCuc作为控制器输入，锂电池输出功率Pbat0作为控制器输出，并将需求功率Pre、超级电容SOCuc和锂电池输出功率Pbat0在其论域上分别分成7个子集、3个子集和7个子集，设计了21条控制规则，各变量隶属函数如图3所示，控制规则如表3所示，模糊控制规则的表面示意图如图4所示。

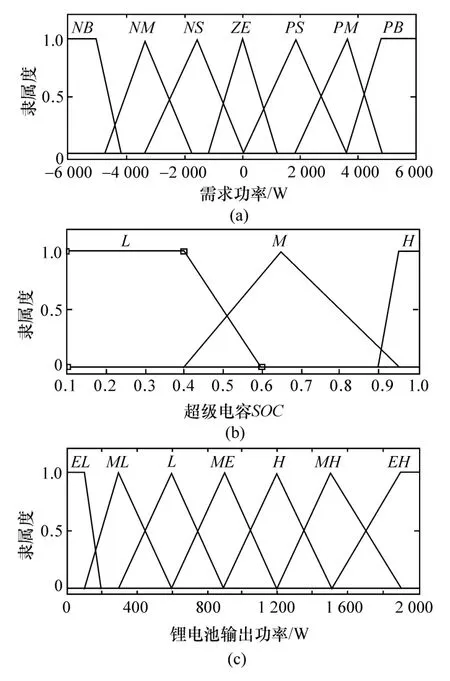
图3 模糊方波控制各变量隶属函数

2.2 功率分配因子模糊控制器设计

功率分配因子模糊控制是复合能源系统中常用的控制方法。设锂电池与超级电容之间功率分配因子分别为Kbat和Kuc，在车辆运动过程中锂电池组输出功率Pbat1与超级电容功率Puc分配满足以下关系：

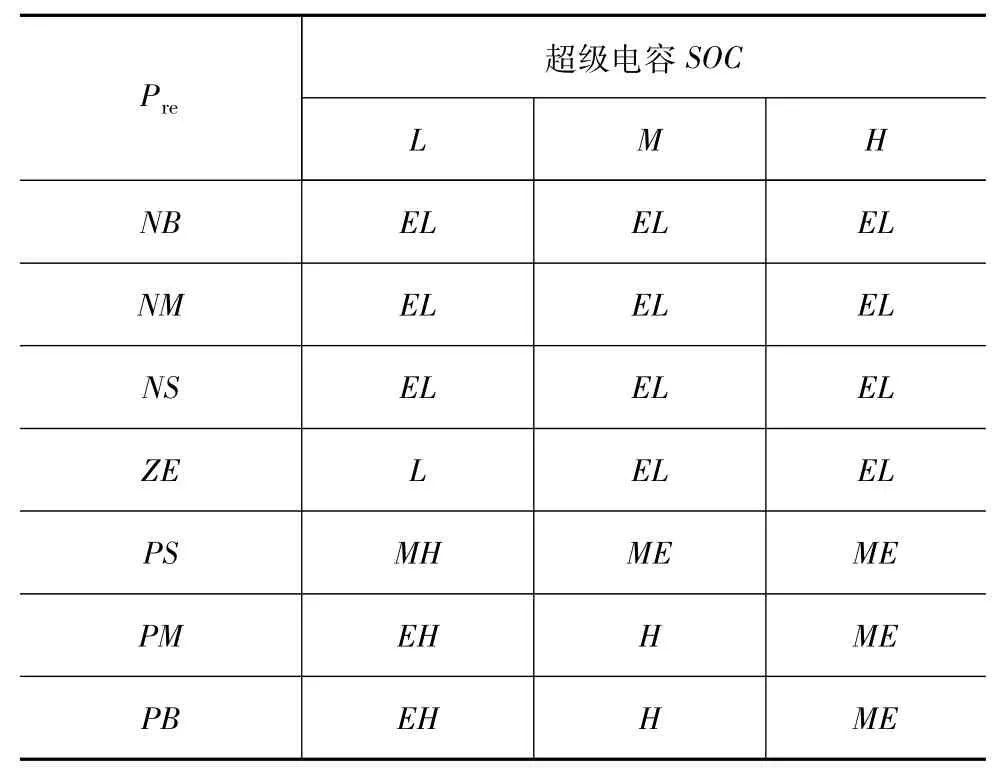
表3 模糊方波控制规则

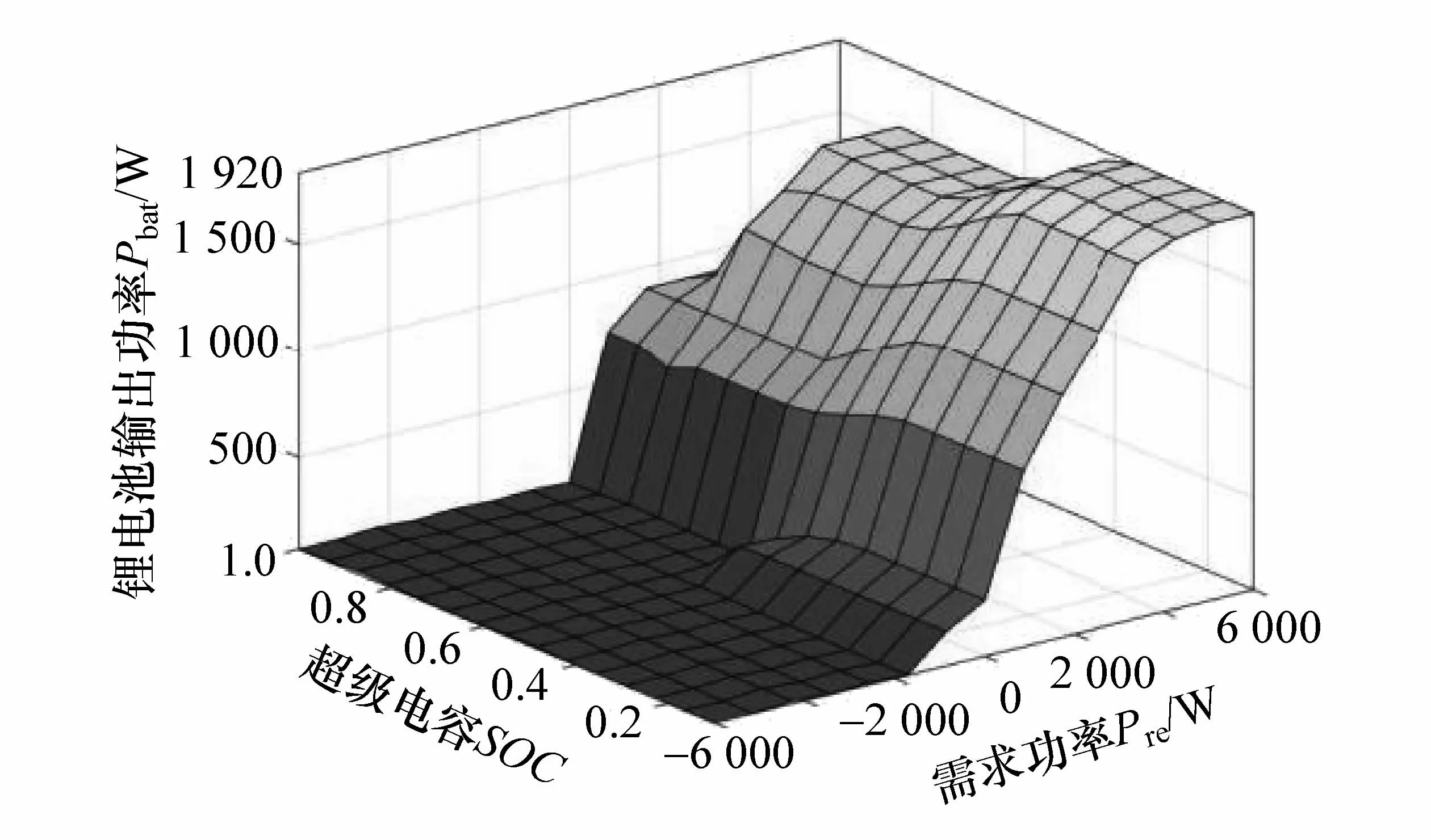
图4 方波调节模糊控制器表面规则图

负载需求功率Pre、锂电池组SOCbat和超级电容SOCuc三者是功率分配因子的重要影响因素，因此本文中将Pre，SOCbat，SOCuc作为功率分配模糊控制器的输入，将锂电池功率分配因子Kbat作为控制器输出。将Pre，SOCbat，SOCuc在其论域上分别分成7个子集、3个子集、3个子集，输出Kbat在其论域上分成7个子集，设置了63个控制规则，各个变量隶属函数如图5所示，控制规则如表4所示，控制器表面控制规则如图6所示。

2.3 基于模糊方波的联合控制器设计

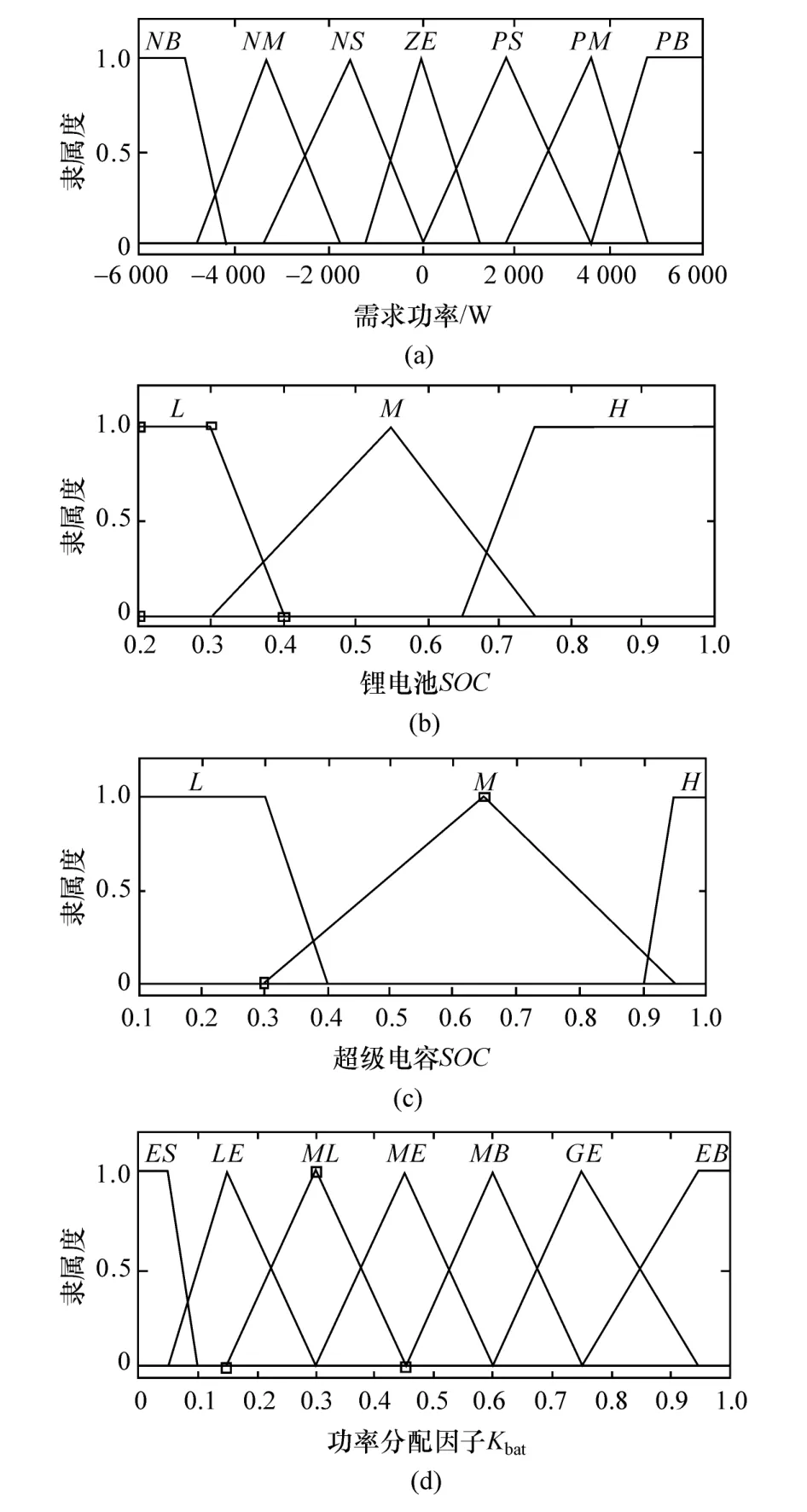
图5 功率分配因子模糊控制各变量隶属函数

从图4与图6可发现，两种模糊控制策略具有完全不一样的特性：（1）功率分配因子模糊控制策略在功率变化时，分配因子变化较大，在功率快速变化的工况下可较好抑制锂电池功率的上升速率，但缺少超级电容充电工况，不利于调节超级电容电压；（2）方波调节模糊控制策略在所有工况下基本维持锂电池输出功率在一个稳定的区间内，具有较好的限幅能力，方波调节模糊控制存在超级电容充电工况，可调节超级电容电压，使其处于良好的工作电压区间，但在需求功率快速变化的工况下，可能因双向DC／DC响应不及时造成锂电池输出功率产生较高幅值尖峰。

对于超级电容＋双向DC／DC的拓扑结构，仅有一个控制对象超级电容，即控制器只有一个输出，在超级电容电压允许的范围内，降低锂电池输出功率是其核心控制思路。本文中设计的联合控制器采用最简单的组合方式：择优输出，两个子控制器中当前时刻超级电容输出功率最大的一个则作为联合控制控制的输出。将模糊方波调节器输出Pbat0和功率分配因子模糊控制器Kbat作以下处理：

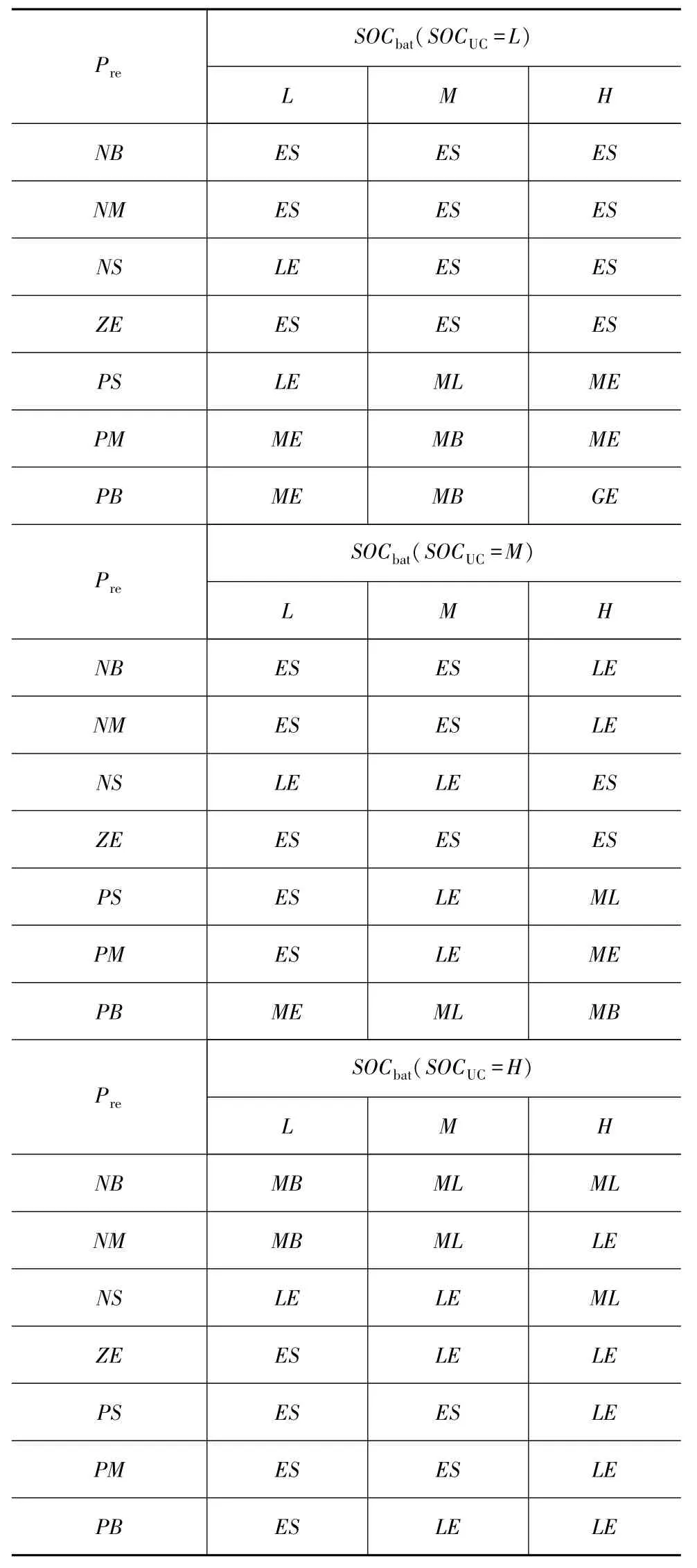
表4 功率分配因子模糊控制规则

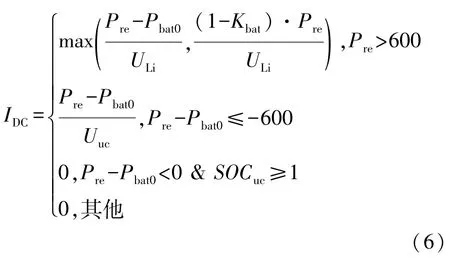
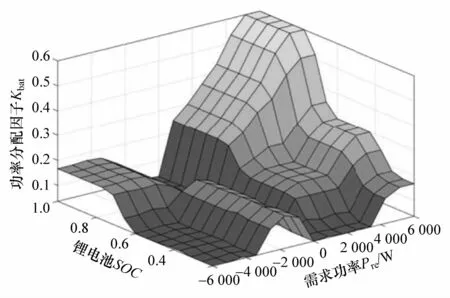
图6 功率分配因子模糊控制器表面规则图

式中：IDC为双向DC的给定电流；ULi为锂电池组电压；Uuc为超级电容端电压。

3 仿真与台架实验结果分析

3.1 系统建模

结合第1章的实验台架实际参数，本文中采用MATLAB下的Simulink仿真环境搭建系统模型。负载模型由实验台架驱动电机实际负载数据组成（母线电压、电流，电机转矩、转速）；以效率为95%、变比为母线电压与超级电容端电压之商的理想变压器为双向DC／DC模型；以锂电池的Rint模型作为锂电池模型（本文中实验用电池组采用实验室恒温空调和机箱自然风冷，温度在30±5℃内变化，因此可理想设定温度为不影响因素，暂不建立热模型），具体模型如式（7）～式（12）所示。

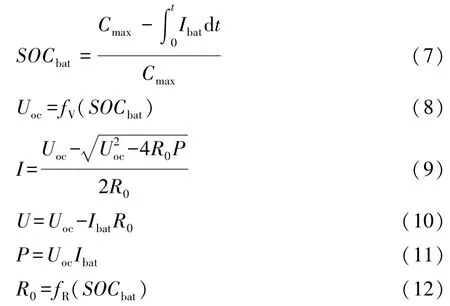
式中：Uoc为电池组开路电压；Cmax为电池组最大容量；fV（SOCbat）与fR（SOCbat）均为实验室实验平台测量数据高次拟合的多项式。

以线性电源和超级电容内阻R1串联的Rint模型作为超级电容模型，其具体模型如式（13）～式（17）所示。

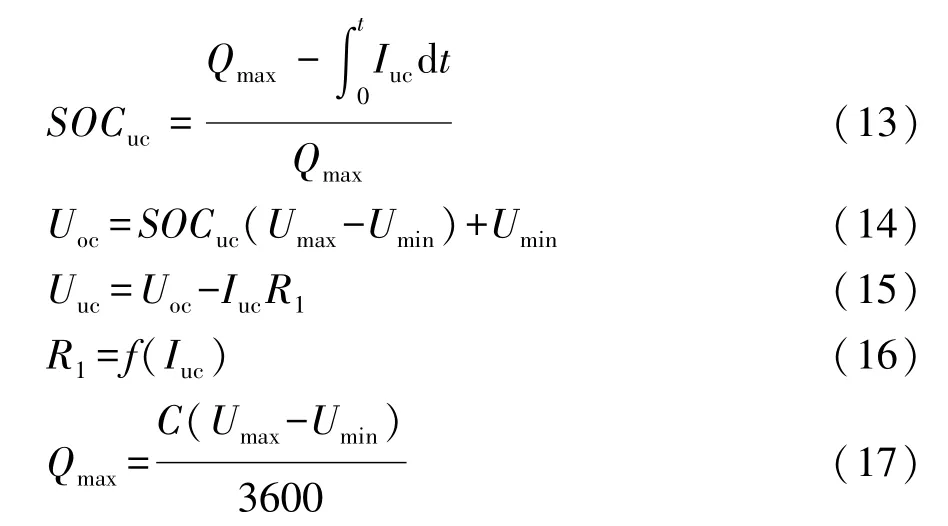
式中：Umax为超级电容最大工作电压；Umin为超级电容截止放电电压；f（Iuc）为实验室实验平台测量数据高次拟合的多项式；Qmax为超级电容最大可用容量；C为超级电容容值；Uoc为超级电容开路电压；Uuc为超级电容端电压。

在MATLAB的Fuzzy Logic模糊逻辑工具箱中生成控制器模糊规则嵌入Simulink仿真环境的Fuzzy模块中，结合第2章中组合单元的设计，组成能量管理控制器。仿真系统如图7所示。

3.2 控制器功率分配性能对比

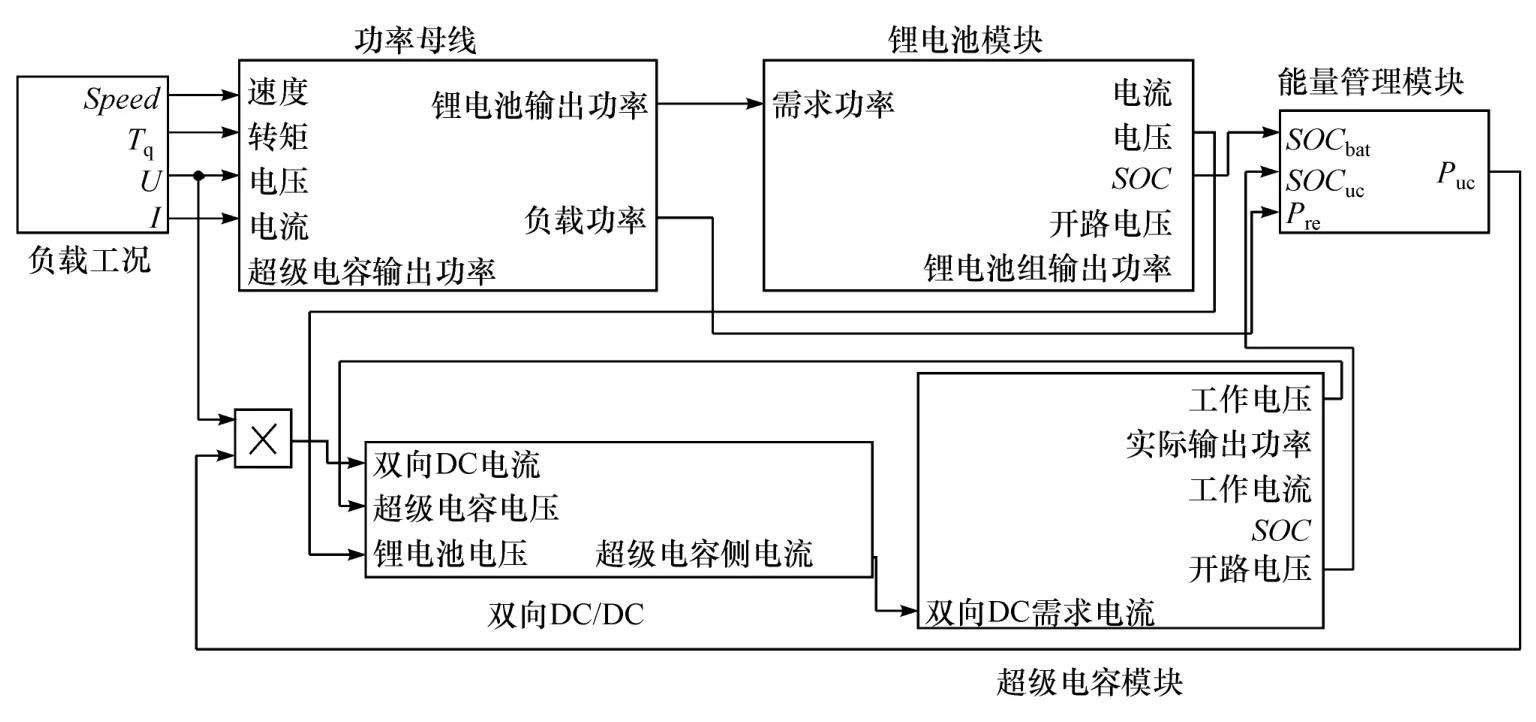
图7 系统仿真

3种控制策略中，模糊方波控制缺少锂电池SOC这一输入变量，因此本文中设定锂电池SOC初始值为0.6，超级电容SOC为1，在此前提下对比3种策略的性能表现。首先对比在5个ECE循环工况下的性能，仿真时间为985 s，步长为0.01 s。仿真结果如图8～图10所示。

图8 ECE工况下模糊方波调节控制

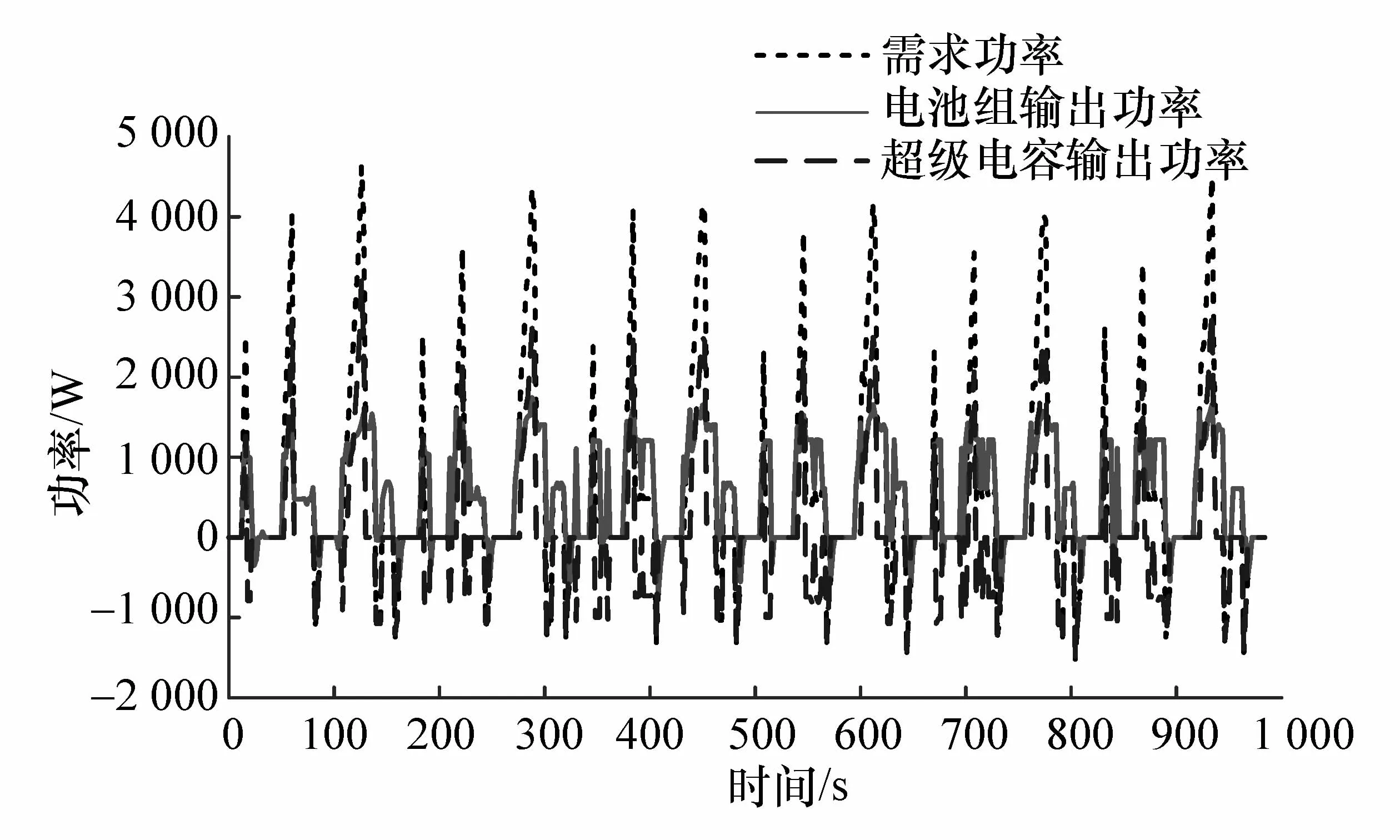
图10 ECE工况下基于模糊方波调节的联合控制

在ECE工况下，3种控制策略性能表现有较大差异：（1）模糊方波调节控制在需求功率变化较大时（如图8中仿真时间为530 s的区间），不能及时抑制锂电池输出功率上升趋势，其他两种控制策略对于需求功率上升率较大的情况均有较好的表现；（2）功率分配因子模糊控制在需求功率幅值Pre＞3000 W时，不能很好抑制锂电池输出功率的上升，会有瞬间超过2 500 W（1C放电）的情况，另两种控制策略均可在任意情况下把锂电池输出功率限制在2 000 W以内；（3）基于模糊方波调节的联合控制结合两者的优点，并且加入了超级电容补电功能可以保持超级电容较好状态，在整个循环工况下，锂电池输出功率可限制到1 900 W以内，保证锂电池工作在更好的工况下。

为进一步对比3种控制器策略的性能差异，使用更为复杂的UDDS工况进行仿真分析，具体结果如图11～图13所示。

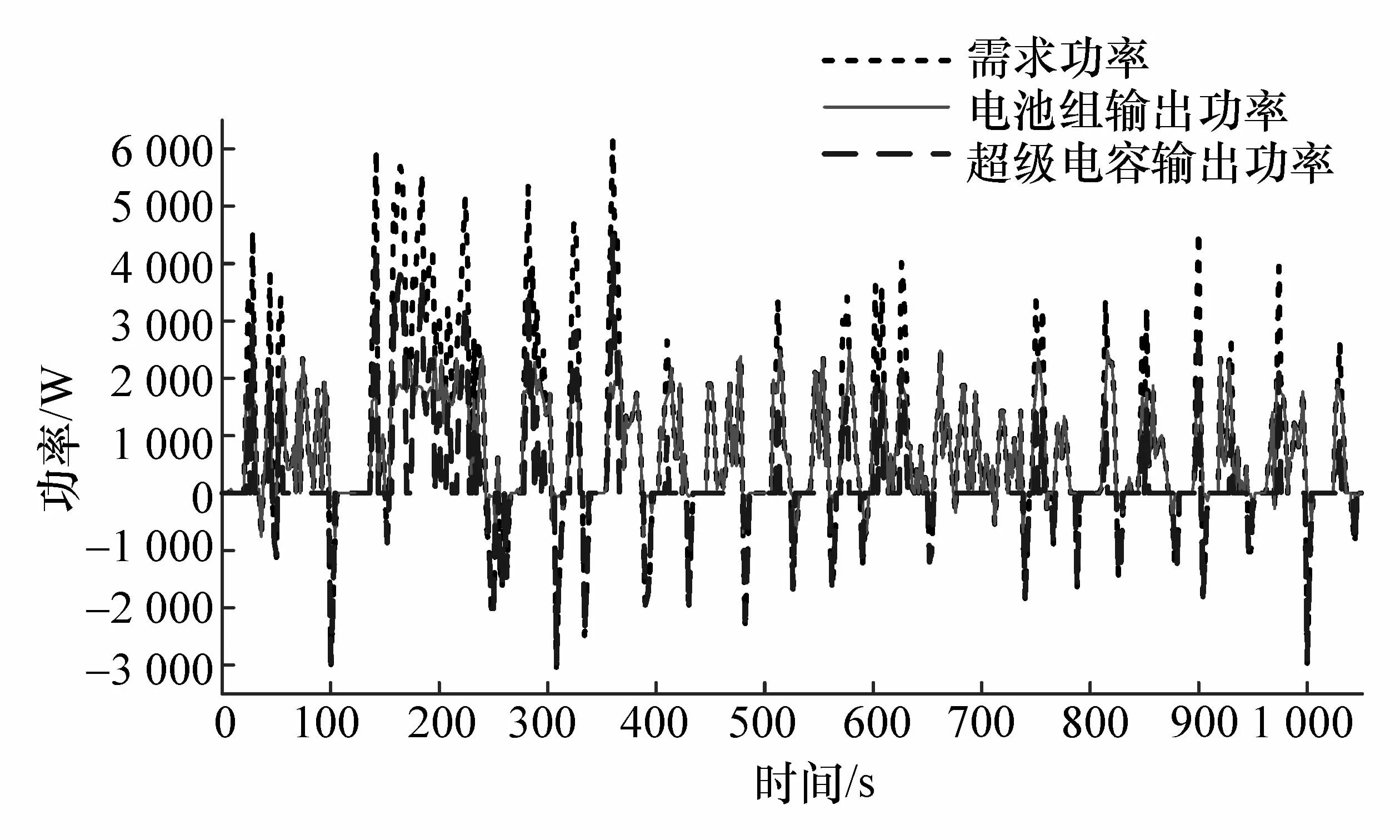
图11 UDDS工况下模糊方波调节控制

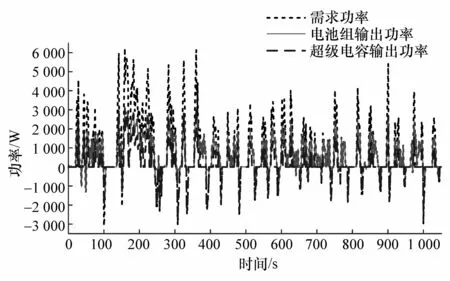
图12 UDDS工况下功率分配因子模糊控制

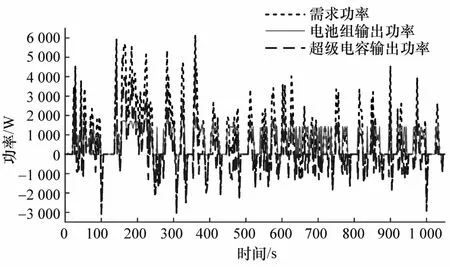
图13 UDDS工况下基于模糊方波调节的联合控制

UDDS工况的极限情况出现在仿真时间150～250 s之间，这段区间内需求功率幅值变化率较大，模糊方波调节控制策略在此区间内把锂电池组输出功率完全控制在2 000 W以下，有利于减少锂电池的衰减；功率分配因子模糊控制下锂电池输出功率在此区间内出现大于3 000 W的情况，并且持续时间较长，加快锂电池衰减速度，而在250 s后，由于需求功率幅值相对较小，功率分配因子模糊控制对锂电池输出功率限幅能力比模糊方波调节控制表现得更好；对于基于模糊方波调节的联合控制在整个UDDS工况下，把锂电池输出功率基本保持在2 000 W左右且通过超级电容完全吸收回馈能量，既维持了超级电容处在较好的输出状态，使锂电池处于一个相对稳定的状态，还大大减小电池的时安累积，从而降低电池衰减。

另外，基于模糊方波调节的联合控制策略能够根据锂电池SOC自动调整锂电池最大输出功率，对锂电池SOC为0.6，0.3时的控制效果对比分析，以UDDS工况为例，锂电池输出功率和超级电容输出功率分别如图14和图15所示，超级电容SOC的变化曲线如图16所示。

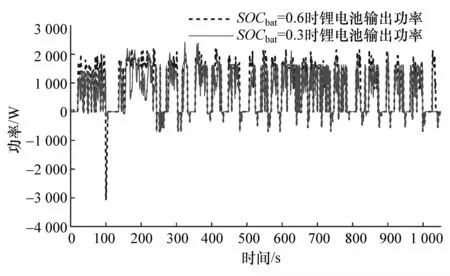
图14 锂电池SOC不同时锂电池输出功率对比

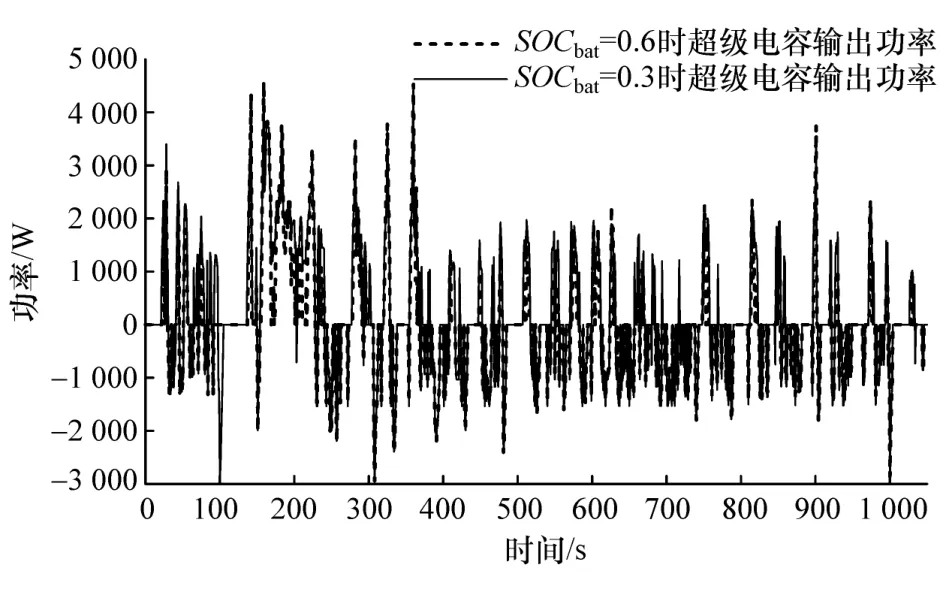
图15 锂电池SOC不同时超级电容输出功率对比

图16 锂电池SOC不同时超级电容SOC变化对比

在锂电池SOC下降时，图15和图16充分反映了基于模糊方波调节的联合控制策略会进一步限制锂电池的输出功率，增大超级电容输出功率，减少因锂电池SOC低时内阻增大而产生的焦耳热，便于电池组热管理系统控制电池温度，使电池工作在适温条件，降低电池衰减速度。

3.3 不同控制策略下的锂电池衰减率对比

为更加科学细化地衡量3种控制策略的性能，本文中引入电池衰减率作为一项对比指标（仅考虑电池衰减，超级电容衰减率极小，不作考虑），通过用SOH的减少量来表示，记作Qloss。通过引用文献［11］中辨识后的Arrhenius模型作为磷酸铁锂电池的衰减模型，具体模型如式（18）所示。

式中：C_Rate为电池充放电倍率；R为气体常数，取8.314 J／（mol·K）；Tbat为电池温度，K，由于本文中电池组所处实验条件基本可恒温在30±5℃，因此取30℃作为定值；Ah为电池电流的时安积分，A·h。根据电池损伤累积理论，可将式（18）转换为

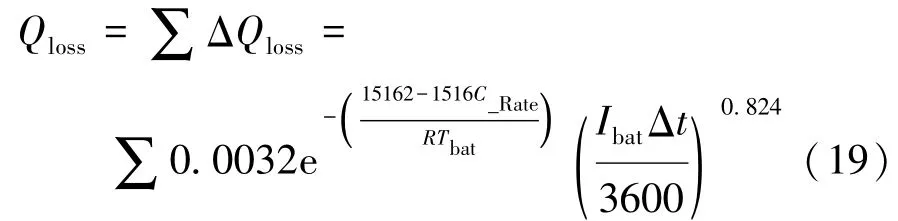
由式（19）分别计算3种控制策略在5个ECE工况后和1个UDDS工况后的锂电池组衰减率。具体结果如表5所示。

通过数据对比，基于模糊方波调节的联合控制策略，在两种工况下，锂电池衰减率均为最低。对比模糊方波调节控制策略，在ECE工况下，衰减率下降2.29%，在UDDS工况下，下降15.21%；对比功率分配因子模糊控制策略，在ECE工况下，衰减率下降5.4%，在UDDS工况下，下降16.58%。可见基于模糊方波调节的联合控制结合了各个组合成员的优点，可更好地提高控制性能。

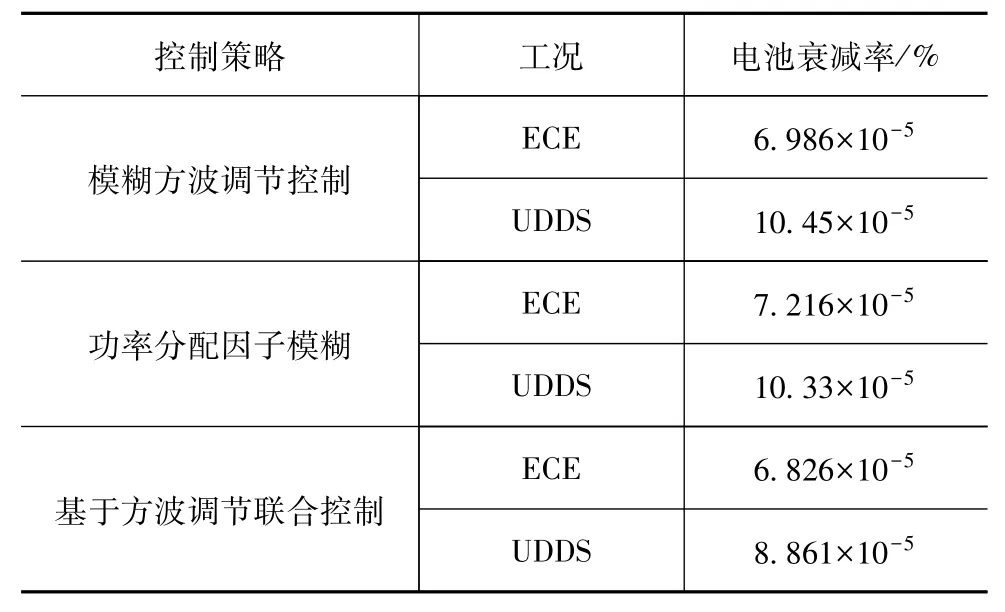
表5 不同控制策略下的锂电池衰减率对比

3.4 能耗与使用成本对比

考虑到双向DC／DC的效率（本文中取效率值为0.95）问题，若超级电容经常需要锂电池补充能量会存在较高能量损耗，降低汽车续航里程，因此控制策略必须保证在超级电容能耗较小的情况下达到控制目的。在本文的设计中，超级电容尽量通过制动回馈充电。

分别对比3种控制策略在ECE工况和UDDS工况下锂电池组和超级电容总能量消耗情况，如表6所示。

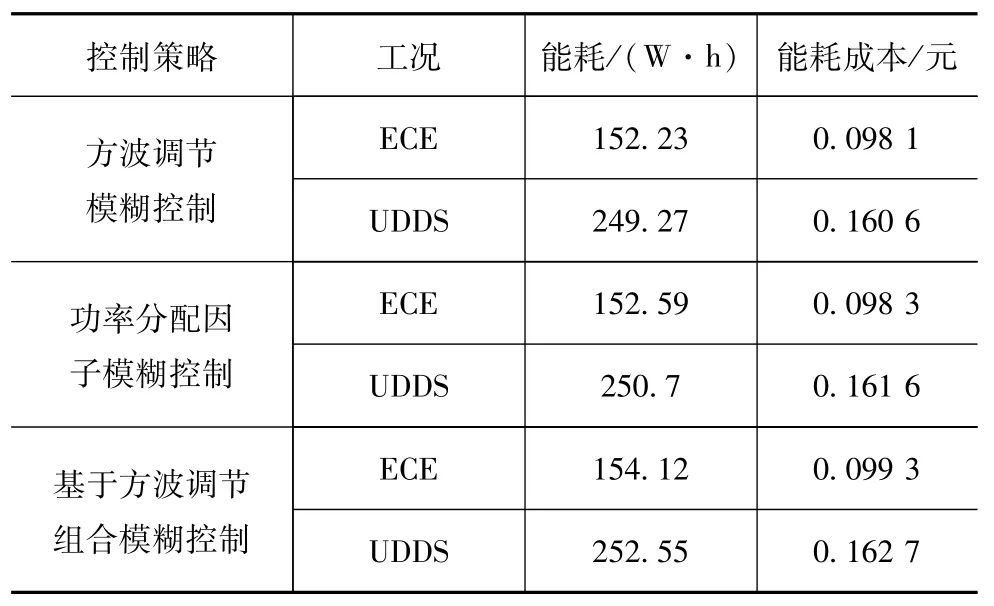
表6 能耗数据

分析实验结果可发现，基于模糊方波调节的联合控制策略在两种工况下，能耗均高于其余两种控制策略，在ECE工况下，对比模糊方波调节控制器，能耗增加1.52%，对比功率分配因子模糊控制，能耗增加1.31%；在UDDS工况下，对比模糊方波调节控制器，能耗增加0.7%，对比功率分配因子模糊控制，能耗增加1.03%。这也验证了降低能耗与降低电池衰减率是一对矛盾目标。

为此，本文中采用使用成本来衡量能耗与电池衰减率这对目标的优劣，使用成本=能耗成本＋电池衰减成本。本文中以某40 A·h磷酸铁锂电池单价为340元／块、市价电费0.58元／（kW·h）、充电效率为0.9计算得到3种控制策略在不同工况下的使用成本，如表7所示。通过数据分析，基于模糊方波调节的联合控制策略在两种工况下，使用成本均为最低。对比模糊方波调节控制，在ECE工况下，使用成本基本一样，在UDDS工况下，下降1.92%；对比功率分配因子模糊控制策略，在ECE工况下，使用成本下降0.38%，在UDDS工况下，下降2.15%。

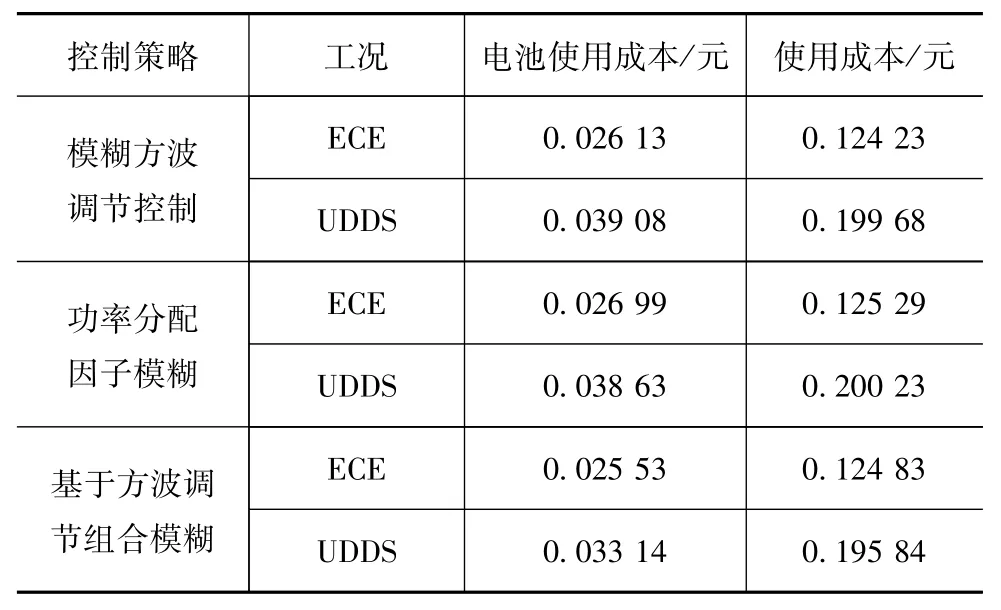
表7 系统使用成本

通过以上一系列的对比，相对于单一模糊控制策略，基于模糊方波调节的联合控制策略具有更好的控制性能，达到了设计目的。为进一步验证本文中提出的改进控制算法的可行性，需在实际硬件平台复现仿真结果，因此需搭建硬件在环实验平台进行实验分析。

3.5 实验台架结构

本文中的实验台架通过使用测功电机和驱动电机分别模拟电动汽车的道路状况和汽车动力，如图17所示。图中工控机1相当于电动汽车中的整车控制器，控制整个动力系统；工控机2为路况模拟机，用于控制三相异步电机和变频器，实现路况模拟。台架实物如图18所示。

3.6 台架实验结果及分析

图18 台架实物图

在实验台架工控机1的控制软件中嵌入基于模糊方波调节的联合控制策略，分别在ECE和UDDS工况下进行验证。实验初始条件作预先设定，锂电池初始SOC分别为0.6，0.3，由于系统设计原因超级电容初始SOC最高为0.8。实验结束后将实验数据库导入到Simulink中绘制出实验结果，如图19～图23所示，功耗与电池估计衰减率如表8所示。

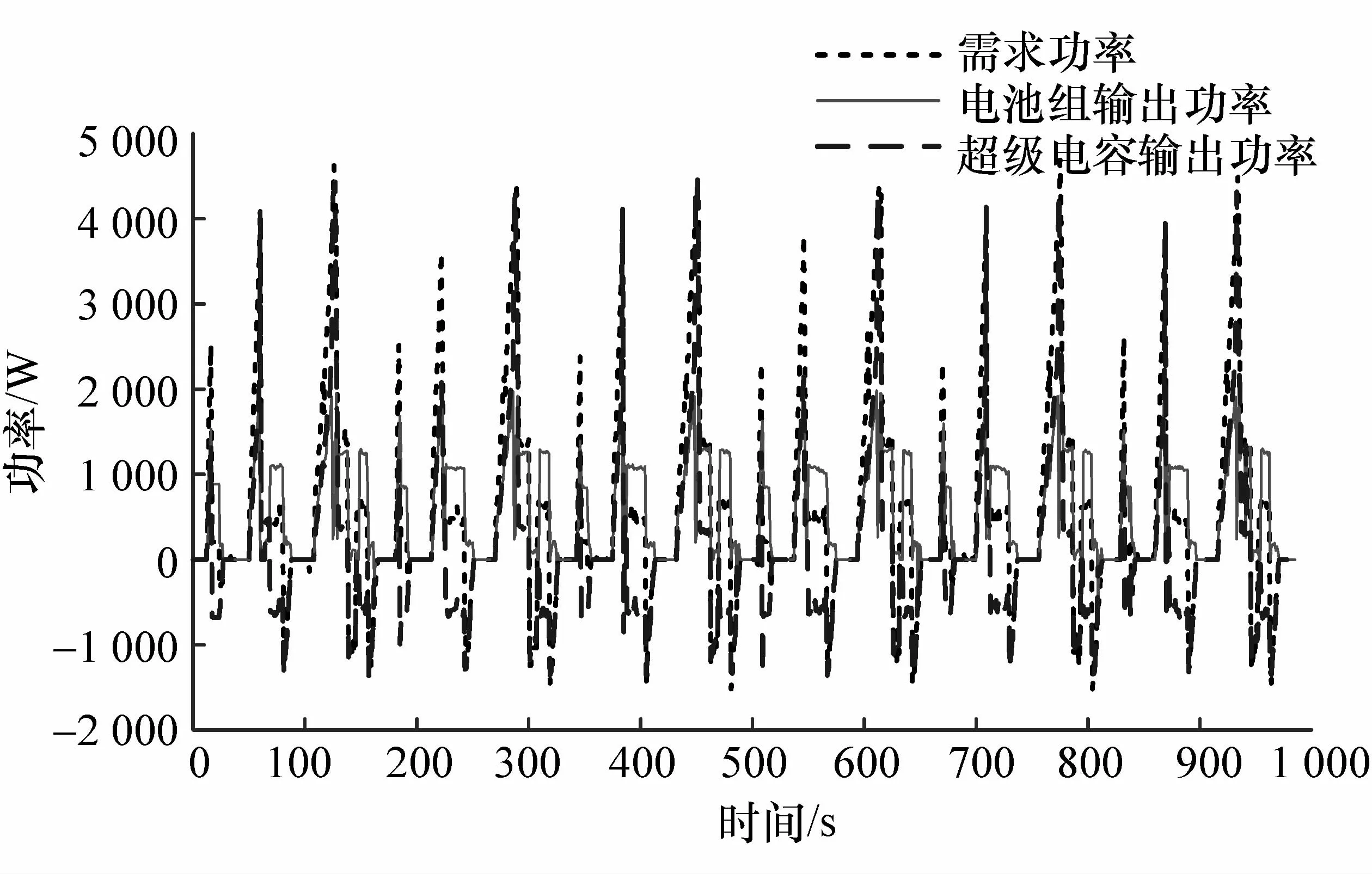
图19 电池SOC为0.6时ECE工况下实验结果

图20 电池SOC为0.6时UDDS工况下实验结果

对比实验结果与仿真结果，在ECE工况下，实际实验结果与仿真结果基本吻合，由于实际台架的双向DC／DC存在响应延时和超调等问题，在回馈制动初始阶段，存在超级电容吸收能量大于制动回馈能量，出现短暂的电池放电；在UDDS工况下，也由于同样原因，在150～250 s的时间内，需求功率变化剧烈，超级电容处于过度输出状态，但整体基本符合仿真结果。

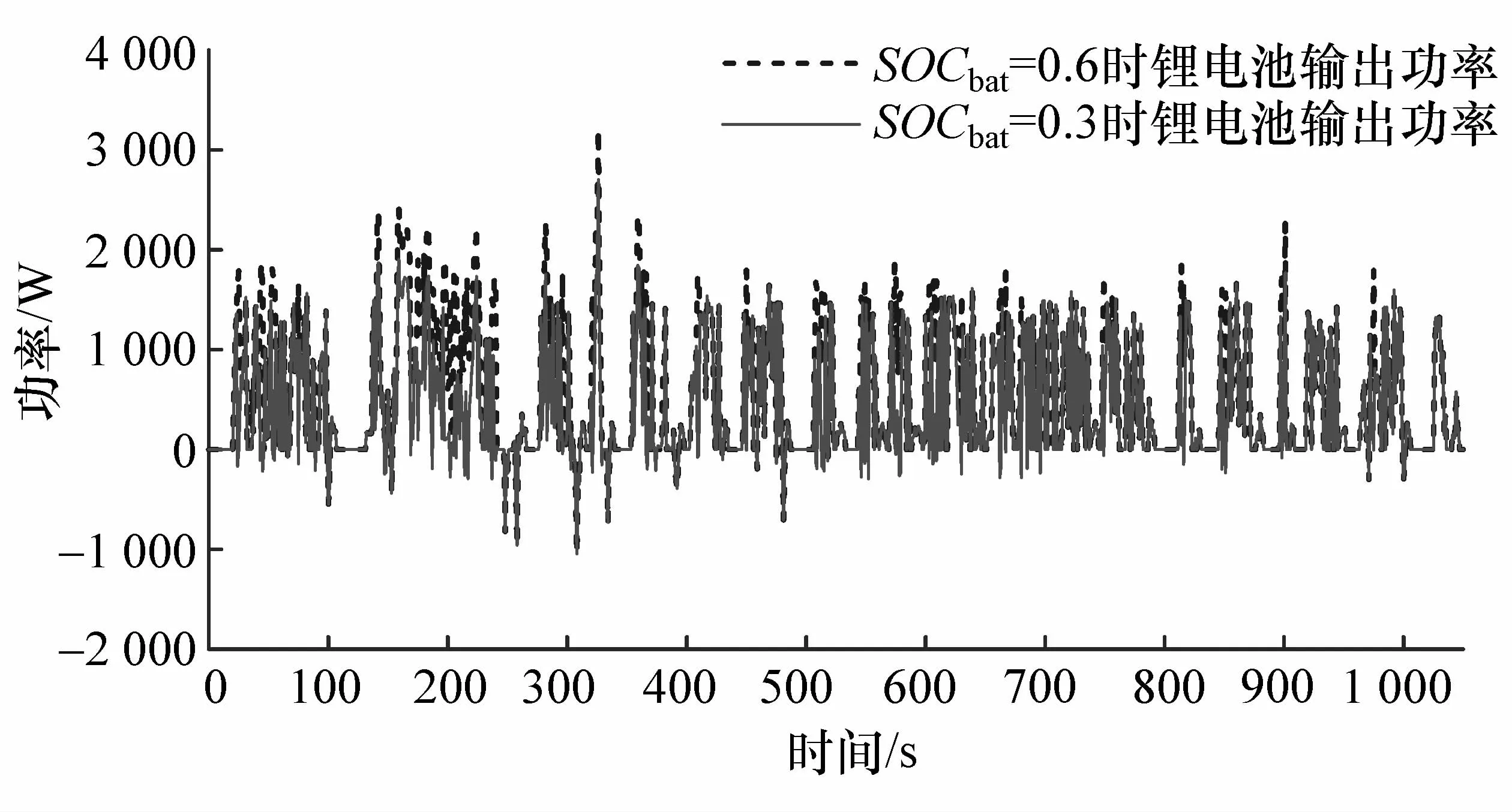
图21 电池SOC不同时锂电池输出功率对比

图22 电池SOC不同时超级电容输出功率对比

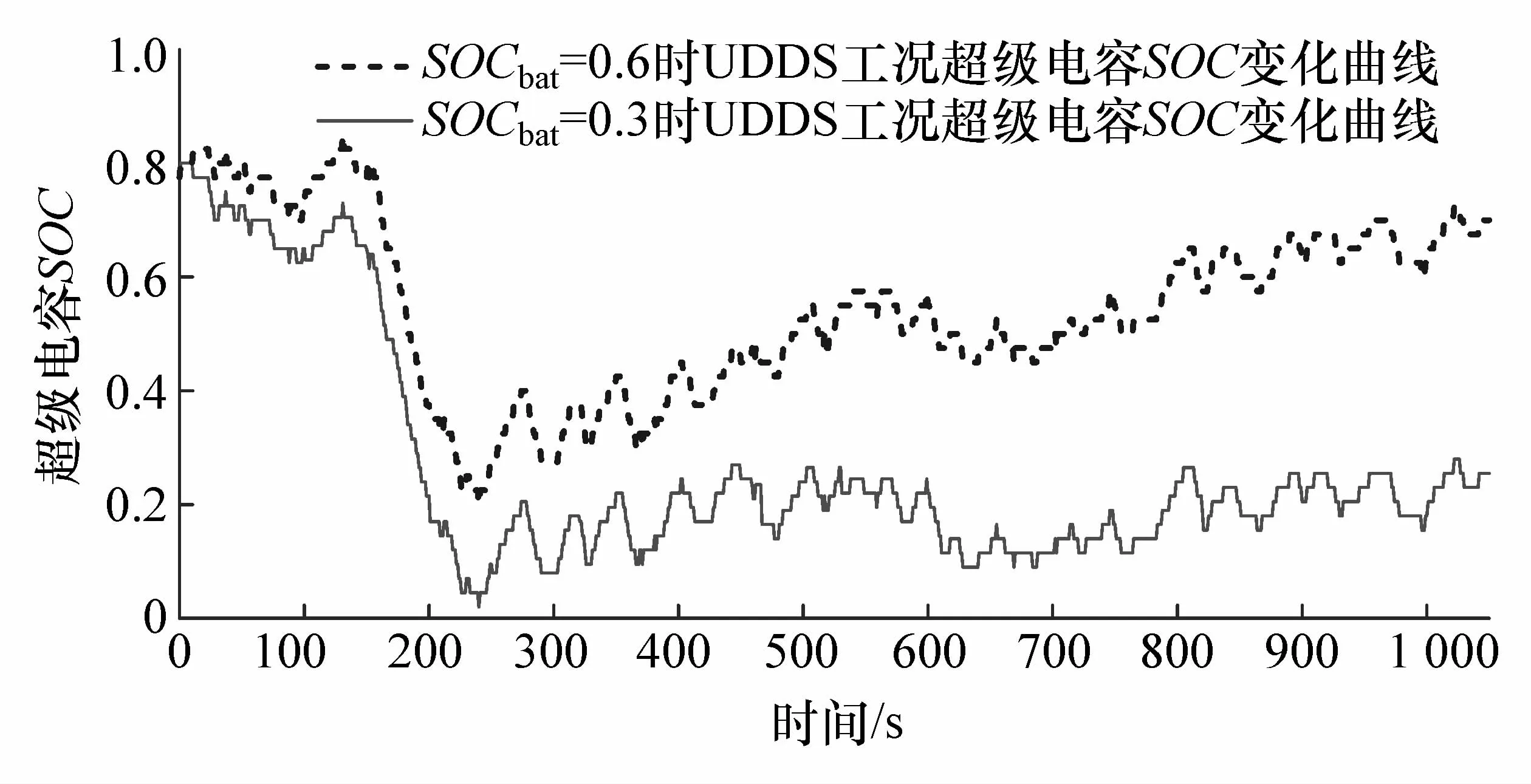
图23 电池SOC不同时超级电容SOC变化对比

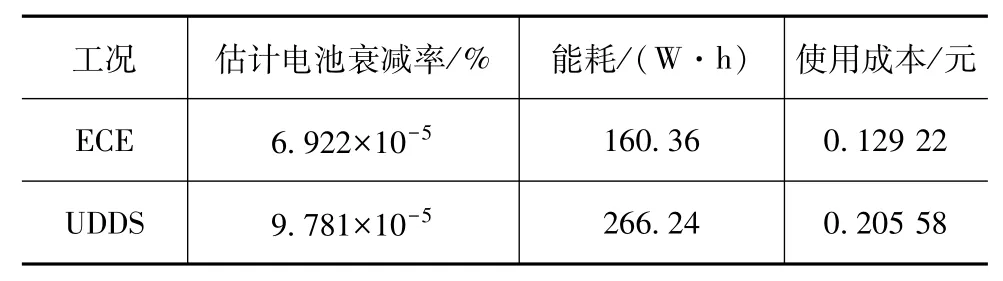
表8 实验功耗与电池衰减数据

由表8可见，在两种工况下，台架实验功耗与电池衰减率估计值均大于表6和表7中的仿真数据，但相差并不大，在ECE和UDDS工况下使用成本较仿真结果分别增加了3.51%和6.26%。这反映出仿真对双向DC／DC建模存在不足，其效率95%仅是平均值，可是实际使用功率区间内，效率会低于平均值，导致电池时安积分增大且功耗上升，双向DC／DC实际性能是造成实际与仿真不一致的主要原因之一。

对比UDDS工况下锂电池SOC为0.6和0.3时的台架实验结果，两种情况下锂电池输出功率和超级电容输出功率分别如图21和图22所示，超级电容SOC变化如图23所示。

从图21～图23 3个维度对比，可验证基于模糊方波调节的联合控制策略在台架实验中锂电池SOC不同时也可取得与仿真基本一致的性能。

4 结论

通过仿真对比，本文中把控制效果较为明显的基于模糊方波调节的联合控制策略成功嵌入到实际的实验台架中，并得到了较好的控制效果，在能量损耗与电池衰减速度之间找到一个较好的平衡点，降低了系统使用成本，实现了设计期望的效果。但是由于在仿真模型中没有考虑到系统的通信延时问题以及双向DC／DC的实际模型问题，造成实际实验出现与仿真结果不太符合的地方。在今后进一步的研究中将会重点考虑系统的响应时间和仿真模型优化问题。