带有收获项的捕食模型的稳定性及Hopf分支

徐 辉，李年蛟

（1.安徽工商职业学院公共课教学部，安徽合肥231100；2.池州学院数学与计算机学院，安徽池州247000）

早在1926年Lotka和Volterra首先在他们的学术论文[1]中提出一个微分方程组可以用来刻画捕食者和食饵之间的关系。此后，一些捕食-食饵模型被生物学家和数学家大量提出并被广泛的研究。特别是在近些年，随着经济社会的发展，人们往往更加注重考虑对生物资源开发的最大收获效益，比如在渔业、畜牧业等方面。因此，在捕食-食饵模型中考虑收获率更具有合理性和现实性。在文献[2]中作者系统地研究了一类捕食者带有常数收获率的捕食-食饵模型。通过理论分析他们得到了不同类型的分支，比如鞍-结点分支、Hopf分支及其余维2和3的Bogdanov-Takens分支等动力学行为。他们的结果表明带有收获率的捕食-食饵模型比不带有收获率的捕食-食饵模型更具有丰富的动力学行为。另外，在文献[3]中作者研究了一类捕食者带有线性收获项的捕食-食饵模型。在该文中作者分析并证明了通过参数值的变化系统可以呈现出不同的动力学行为。事实上，带有线性收获率比带有常数收获率更具有一般性。最近，在文献[4]中研究了一类捕食者带有非线性收获率的捕食-食饵模型。在该文中作者利用线性稳定性分析给出了正平衡点的稳定性以及利用中心流形定理、标准型方法给出了Hopf分支的分支方向等动力学问题。

本文主要是研究一类带有收获项的捕食—食饵模型，即：

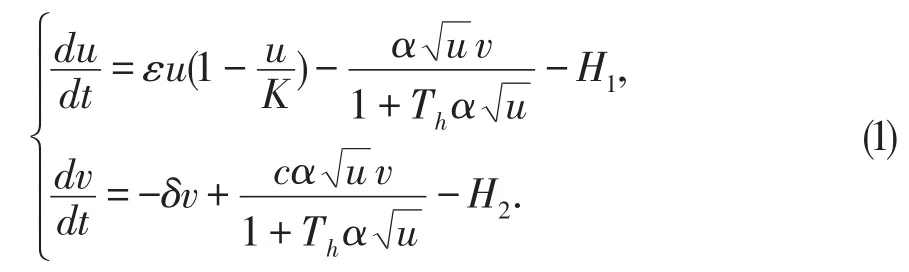
这里，u,v分别表示食饵和捕食者的种群密度；ε表示食饵的內禀增长率；K是环境的最大承载值；α表示捕食者对食饵的搜索效率；Th代表每个食饵的应对时间；δ表示捕食者的自然死亡率；t表示时间并且我们假设ε，K，Th,α,c和δ都是正常数。此外，H1和H2分别表示食饵和捕食者的收获率。若令H1=0并且H2=0，即食饵和捕食者不带有收获项。文献[5]中研究了该情形下的平衡点的稳定性并研究了在随机环境下食饵种群的出生率和捕食者种群的死亡率会受到高斯白噪声的干扰。最近，文献[6]中研究了食饵、捕食者分别带有常数收获率，即H1=h1和H2=h2，这里的hi≥0,(i=1,2)。在该文中分别研究了平衡点的存在性和稳定性，并研究了Bogdanov-Takens分支、Hopf分支等动力学问题，这些研究结果无疑丰富了对系统（1）的研究。然而，一方面，从生物和经济收益角度来说常数收获率并不具有更现实的实际意义。另一方面，在自然界中常数率收获项并不是总是发生，换句话讲，常数项收获并不具有一般性。基于此种考虑，在本文中引入线性收获率，即令H1=0并且H2=ev，这里e为正常数。在讨论前，为方便起见引进一组无量纲变换：

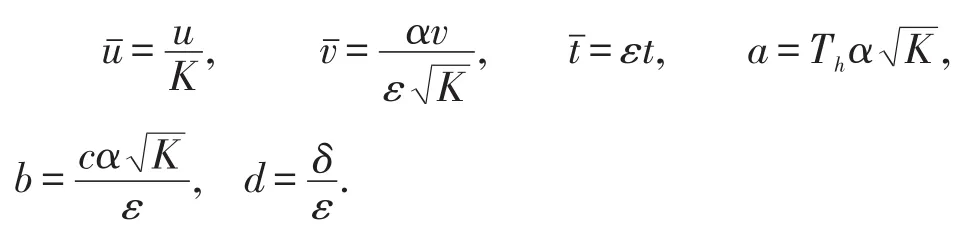
事实上，若令a=0，即每个食饵的应对时间恒为零并且记则此时系统（2）可以表示为如下系统：

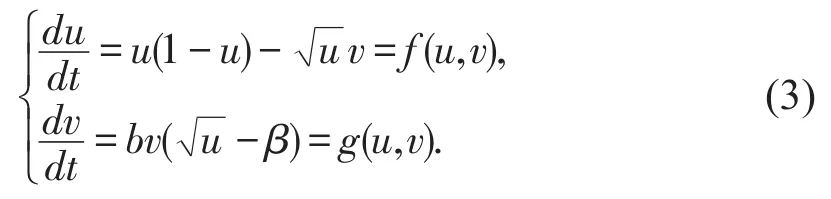
因此，在接下来的讨论中将进一步研究系统（3）的有关动力学行为。

1 正平衡点的存在性及其稳定性

为了得到系统（3）的平衡点，需要令（3）式的右端恒为零，即：

经过计算，可以得到系统（3）有两个边界平衡点E1=(0,0)，E2=(1,0)和一个正平衡点E*=(u*,v*)=(β2,β(1-β2))，这里当且仅当 0＜β＜1成立。出于对现实生物意义的考虑在本文中不再研究边界平衡点E1和E2的动力学行为并且在下面的讨论中，条件0＜β＜1总是成立的。

系统（3）在正平衡点E*=(β2,β(1-β2))处的雅可比矩阵为：

事实上，（5）的特征值可以由下面的特征方程决定：

这里

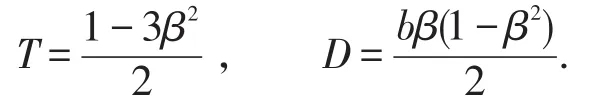
则方程（6）的两个根可以表示为：

据前面的假设如果0＜β＜1成立，则此时D＞0总是成立的，这表明方程（6）有两个同号的特征根。因此，正平衡点E*的稳定性由T的符号决定。

于是我们有下面的结果：

定理1若不等式0＜β＜1成立，则

（2）类似（1）的证明，从略。

为了验证理论分析结论的正确性，用数学软件Matlab进行数值模拟，如图1所示。选取参数，时间t分别取为1、10、100和300，初始值取为 (0.3,0.34)，此时正平衡点E*=(0.36，0.384)。通过数值模拟，从图1中可以看到随着时间的增加轨线逐渐收敛到正平衡点E*，即此时正平衡点E*是渐近稳定的，与理论分析相吻合。

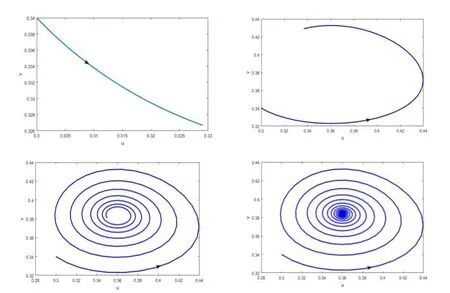
图1 渐近稳定的正平衡点E*

2 Hopf分支及其分支方向

在这一部分将给出Hopf分支发生的必要条件及分支的方向。事实上，通过定理1易知雅可比矩阵J在E*上有一个纯虚根当且仅当。这是Hopf分支发生的必要条件之一，因此在下面的讨论过程中把参数β作为主要的分支参数。所以当参数β充分接近临界值βH时，方程（6）会出现一对纯虚根，即：

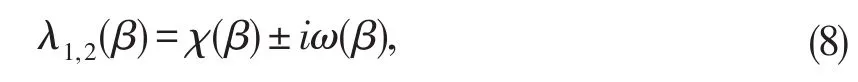
这里

且

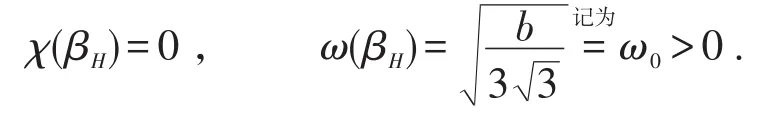
此外，我们可以得到

总结以上两个方面利用Poincare-Andronov-Hopf分支理论可以知道当β=βH时系统（3）在正平衡点E*上会发生Hopf分支。

当β=βH时系统此时方程（6）会出现一对共轭的纯虚根，这是因为系统打破了时间上的对称性，打破时间对称后的系统会出现极限环。数学上把Hopf分支称为超临界的如果系统打破时间对称由Hopf分支产生的极限环是渐近稳定的，否则称为亚临界的。因此，在Hopf发生的条件下研究极限环的稳定性是十分必要的。将应用中心流形定理和标准型理来研究极限环的稳定性。为此，首先将正平衡点E*平移到原点，即作变换。为方便起见，记为u，v，则原系统（3）可以重新写成：

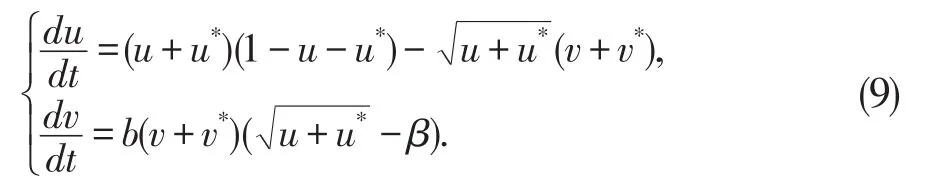
此即

这里

这里O(4)表示u和v大于或等于四次方幂的全体集合。于是当β=βH时，我们可以得到：

容易得到

令

则有

将（11）带入（10）且仍然记u1，v1为u，v并注意β=βH，则可以得到：

经过计算可以得到

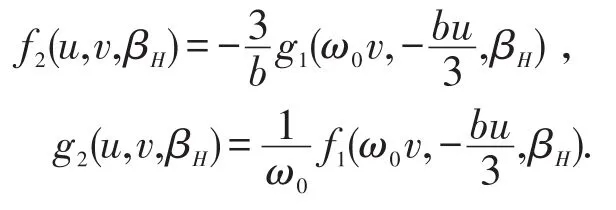
为了决定由Hopf分支引起的极限环的稳定性，通过文献[7]得到表达式σ的符号。这里

且所有的偏导数都在分支点(u,v,β)=(0,0,βH)处求得。通过计算可以得到：

经过计算得：

这里

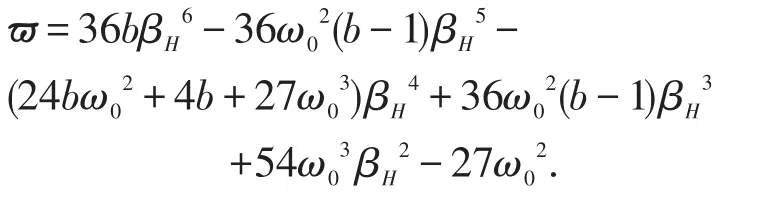
因此，σ的符号由ϖ来决定。

总结以上分析可以得到如下定理2。

定理2当β=βH时系统（3）在正平衡点E*上发生Hopf分支。此外，Hopf分支的方向是超临界的如果

(H1)σ＜0（即ϖ＜0），

并且Hopf分支的方向是亚临界的，如果

(H2)σ＞0（即ϖ＞0）。

注：若条件(H1)成立，则此时由Hopf分支引起的极限环是渐近稳定的；否则，即条件(H2)成立，则此时由Hopf分支引起的极限环是不稳定的。

图2 超临界Hopf分支

为了验证定理2结论的正确性，取参数b=1，时间t分别取为 1、10、100 和 300，初始值为(0.3,0.35)。此时正平衡点且ϖ≈-0.1030（即σ＜0）。如图2所示，随着时间t的增加最终会形成一个稳定的极限环，即此时的Hopf分支是超临界的这与我们的定理相吻合。

3 讨论

本文主要研究了一类带有收获项的捕食-食饵模型。通过理论分析得到了系统当0＜β＜1时存在正平衡点E*（事实上是唯一的正平衡点）并得到了E*稳定和不稳定的充分条件。之后利用中心流行定理和标准型的方法得到了Hopf分支的分支方向，即超临界和亚临界情形。事实上当系统发生Hopf分支时，Hopf分支的分支方向取决于参数b的值。通过数值模拟发现当0＜b＜1时，ϖ＞0总是成立的。这就是说当b∈(0,1)时，此时Hopf分支的分支方向总是亚临界的。而当b∈[1,+∞)时，ϖ＜0总是成立的。这就是说此时Hopf分支的分支方向总是超临界的。在本文中令a=0，即每个食饵（被捕食者）的应对时间恒为零，因为在自然界中一些大型猫科动物，比如狮子和猎豹它们往往擅长于偷袭策略以提升捕猎的成功概率，这是自然界中的普遍现象。另外，不同于文献[6]的是在系统（1）中引入了线性收获项即令H2=ev，通过理论分析和数值模拟得到了丰富的动力学行为。