《三角形面积练习课》教学实录

王静文

【教学内容】

浙教版五年级上册第77、84 页。

【教材分析】

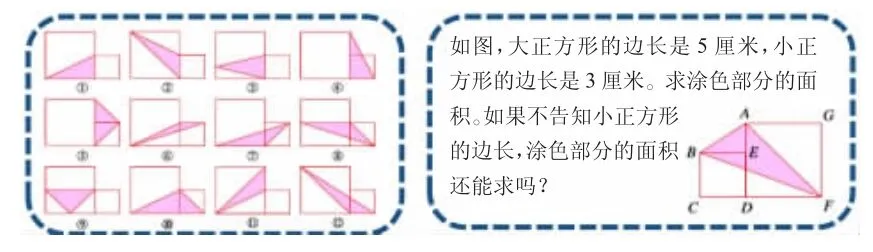
这是一节在学习了三角形面积计算方法后拓展提升型的课。教学的基本思路是：首先，让学生利用两个大小不同的正方形的顶点构建不同形状的三角形，通过计算这些三角形的面积，归纳、发现这些三角形底、高及面积之间的关系（教材第77 页）。接下来，将教材第84 页的练习纳入这些三角形中，主要围绕“等积变形”展开，利用平行线之间的距离处处相等，移动三角形的顶点，将一个面积较难计算的三角形转化成与之等底等高的面积非常容易计算的三角形，使面积计算的方法更加灵活、巧妙（详见下图）。

整节课呈现了有主题、有变式的系列面积计算问题，引导学生在解决问题的实践中探索、生成灵活的方法，体会“转化”的数学思想，丰富和拓展对面积概念的理解。

【教学过程】

一、温故知新

1．引入，布置任务。

师：两个正方形一共有几个顶点？

生：7 个。

师：从7 个点中任意选3 个点依次连线，会构成什么图形？

生：三角形。

师：每个人想三种方案，连点成三角形，并分别计算三角形的面积。

2．学生活动，教师搜集典型作品。

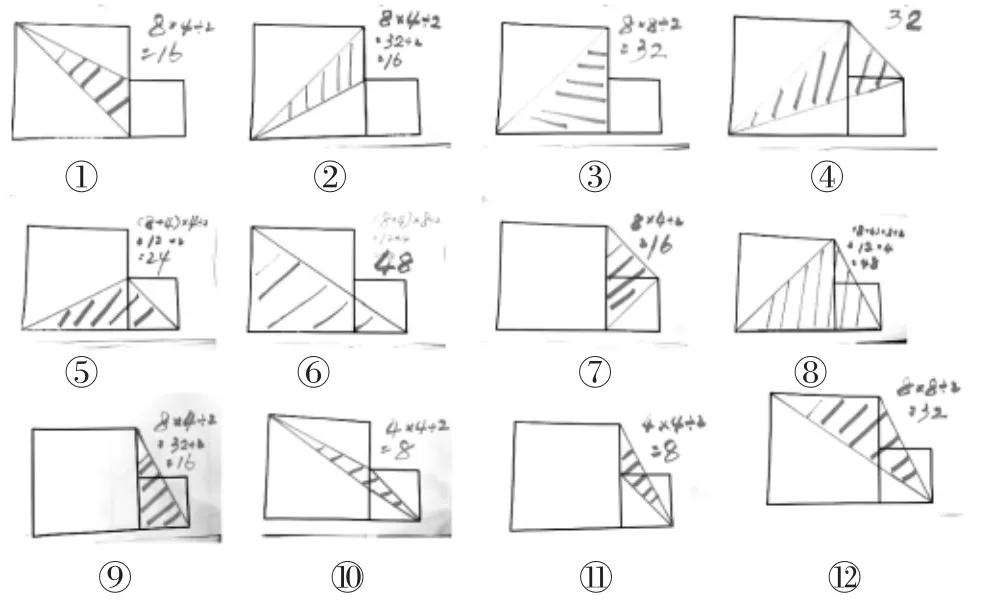
3.分类，梳理方法。

师：如果要给这些作品分类，你打算怎么分？

生：按面积大小分类：①②⑦⑨是一类，面积是16；③④⑫是一类，面积是32；⑥⑧是一类，面积是48；⑤是一类，面积是24；⑩⑪是一类，面积是8。

师：为什么这些三角形的面积是相等的呢？

生：等底等高的三角形面积相等。

师：下面这两个三角形的底和高分别在哪？

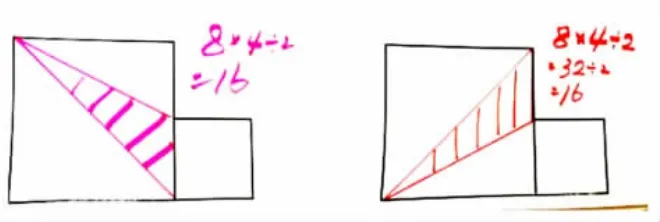
（学生指底和高，让学习能力较弱的学生得到巩固，特别是钝角三角形的底与高）

小结：等底等高的三角形面积相等。

师：面积相等的三角形都等底等高吗？我们以面积是16 的图形为例。

（学生观察、分类）

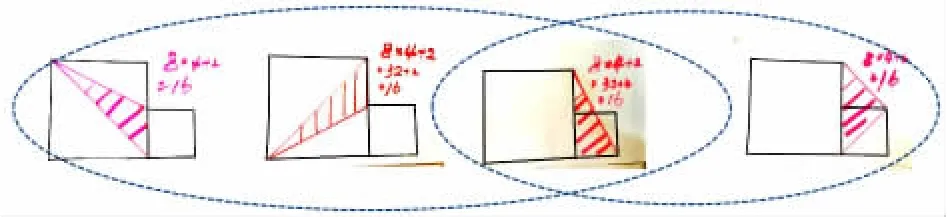
师：看来等底等高的三角形面积一定相等，但是面积相等的三角形却不一定等底等高。

师：我们继续聚焦等底等高的三角形。图⑫里有一个面积是32 的三角形，利用“等底等高”，你能变化出更多面积是32 的三角形吗？

生：利用等底等高的三角形面积相等，底不变，移动三角形的另一个顶点就可以。

师：有道理吗？怎么知道这些三角形的面积都是32？没有变？

生：底没有变。顶点位置虽然在动，都在对应的平行线上，平行线之间的距离处处相等所以面积不变。

小结：利用平行线，可以构造出许多底、高相等的三角形，这些三角形虽形状各异，但面积是相等的。通过观察三角形的底和高的情况，可以更快更好地推断其面积。

【设计意图：这个环节通过学生连三角形，计算面积来复习三角形的面积计算方法，在此过程中强化三角形的底、高等概念；然后，借助“面积相等”的“强刺激”，分类研究，突出“等底等高的三角形面积相等”这一命题；进而，通过多媒体技术，演示三角形等积变形的动态过程，加深学生对平行线之间距离处处相等的视觉印象，为灵活计算特殊三角形面积做好铺垫。】

二、应用新知

1.策略优化和应用。

师：图④为什么面积也等于32 呢？

师：请独立思考两到三分钟，尝试计算。

师：老师看大家都很认真地在想办法。有没有同学遇到了困难？什么困难？

生：底和高都不知道。

师：有没有同学可以解决他的困难？

生：我的办法是整体减空白。

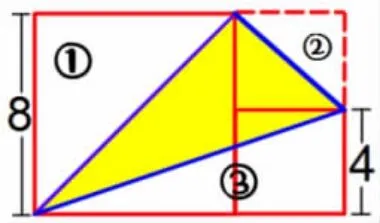
总面积=（8+4）×8=96；

S①=8×8÷2=32；

S②=4×4÷2=8；

S③=（8+4）×4÷2=24

S阴影=96-32-8-24=32。

生：我还有办法。连接正方形的对角线，移动顶点，等积变形，三角形面积等于大正方形面积的一半。

师：有道理吗？想要等积变形，高必须在平行线之间移动。两个正方形的对角线是平行的吗？你是怎么知道的？

生：因为它们都是正方形的对角线，与下底边的夹角都是45°。

师：原来正方形中还隐藏着一组平行线，就是两个正方形的对角线。

［课件再次演示上图：在变与不变中感受面积的关系（拉动顶点）］

师：发现了什么？

生：三角形的面积就是大正方形面积的一半。

师：我们刚刚是怎么将这个面积较难算的三角形转化成一个面积容易算的三角形的？

生：先找到正方形的对角线，利用高在平行线之间相等，移动顶点，转化成同底等高的三角形。

师：要多角度寻找可以利用的平行线，将面积较难算的三角形转化成容易计算面积的三角形。

2.在变化中感受不变，加深对等底等高的理解和应用水平。

师：（边说边演示课件）如果小正方形变得更小呢？小到边长都不知道了，三角形面积还能求吗？如果小正方形变成更大的正方形呢？

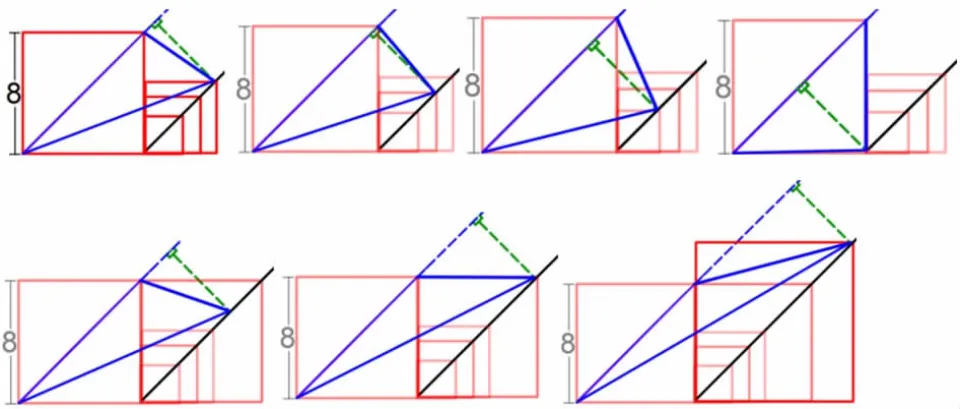
生：三角形的面积只与大正方形有关，是大正方形面积的一半。

生：不管怎么变，三角形的底不变，高度也不变。

师：我们可不可以利用找平行线等积变形的方法快速算出这个三角形的面积？

生：找平行线，等积变形。发现三角形面积是小正方形面积的一半。

师：为什么图④三角形面积是大正方形的一半，图⑩三角形面积是小正方形的一半？

生：因为图④三角形的底是大正方形的对角线，所以面积就是大正方形面积的一半。图⑩三角形的底是小正方形的对角线，面积就是小正方形面积的一半。

【设计意图：通过找隐藏的平行线，灵活应用“等积变形”将底与高未知的三角形转化成与之等底等高且面积易算的三角形，从对等底等高三角形面积相等的简单判断水平提升到灵活应用水平。借助多媒体技术，缩小或扩大正方形的面积，发现平行线之间的距离不变，三角形的面积不变，进一步提高对“等底等高的三角形面积相等”的概括理解水平。同时，也推动学生空间观念更好地发展。】

三、拓展提升

师：如果小正方形移动到大正方形的内部，这时候连接这三个顶点，涂色部分的面积该如何求呢？如果小正方形变成了一个点，将大正方形的四个顶点与之相连所形成的涂色部分面积又是多少呢？

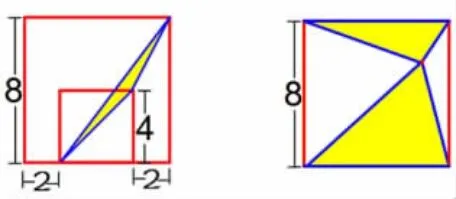
1.学生独立完成。

2.全班交流、反馈。

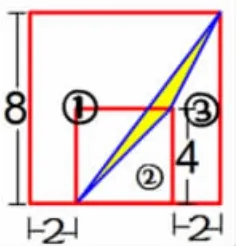
（1）左图交流反馈。

生：整体减空白。

总面积=8×8=64；

S①=（2+8）×8÷2=40；

S②=4×4÷2=8；

S③=（8+4）×2÷2=12；

S阴影=64-40-8-12=4。

生：连接大正方形对角线，等积变形。三角形的面积等于底2 高4 的三角形的面积。

（2）右图交流反馈。

生：S①=S②，S③=S④，S⑤=S⑥，S⑦=S⑧。因此，涂色部分的面积是正方形面积的一半。

生：经过E 点作AB 与CD 的平行线，等积变形，S涂=S△ABE+S△CDE=S△BED，因此，涂色部分的面积是正方形面积的一半。

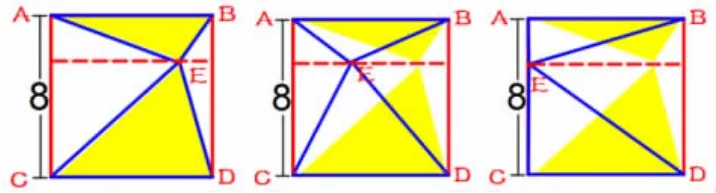
师：我们还可以任意移动E 点，最后可以将涂色部分面积转化成正方形面积的一半。

师：大家觉得这个方法如何？E 点还可以继续移动吗？

生：不论E 点移动到哪（正方形内或正方形上），涂色部分三角形面积都是正方形面积的一半。

【设计意图：这两道题是所学知识的延续与拓展，当小正方形移动到大正方形内部后，之前所学的知识还能解决新三角形的面积计算问题吗？第一题，学生通过思考不难发现两个正方形的对角线仍然是平行关系，仍可利用等积变形解决问题；第二题虽然已经是两个三角形，但利用等积变形可以证明涂色部分三角形的面积之和是大正方形的一半。通过这两道习题的应用和比较，既巩固了前面的学习所得，又让学生惊叹等积变形方法的进一步变化、应用，优势并内化之，使学生对所学知识、方法又有了提升和创新。在解决问题的过程中，发展了学生的空间观念和问题解决的能力。此外，多媒体技术的使用使得学生的想象变得形象、可感，有助于支持、验证和分享学生的猜想。】

四、课堂小结

师：今天我们学习了什么？你有什么收获？

生：今天我们学习了三角形面积的计算。

生：求三角形面积的多种方法。当我们不知道一个三角形的底和高时，我们可以利用等底等高的三角形面积相等将这个三角形灵活地转化成另一个与它面积相等但底和高已知的三角形。

生：我学会了更灵活地计算三角形的面积。

师：“转化”这个词用得好！通过转化，新问题变成了老问题，复杂问题变成了简单问题。

【设计意图：课堂总结不仅回顾了三角形面积的计算方法，更重要的是让学生体会到数学知识之间的联系，数学方法灵活运用的乐趣，在学生心中“种”下了“转化”的数学思想。】

【编辑点评】

王静文老师的这节《三角形面积练习课》在题目的设计和技术的使用方面给人以特别的启发。

第一，题目的设计体现了变式教学的精髓。

练习内容决定了练习的深度。整理全课练习题：1.开放性问题：从相连正方形的7 个顶点中任取3个，构成三角形并计算其面积（下图1）；2.基于讨论，引出“等底等高”的话题，并进一步聚焦其中一个较难求取面积的三角形图（下图2）；3.水平变式题1（下图3）；4.水平变式题2（下图4）；5.开放探究题（下图5）：涂色部分两个三角形的面积和怎样计算好？所有题目，围绕着“等积变形”（主要是“等高”变形）的主题既相互联系又变化发展，全面丰富了学生对于“等高”的概念变式，设置了学生解决三角形“等积变形”问题的过程变式，切实增进了学生思考的深度、广度和灵活性。

图1

图2

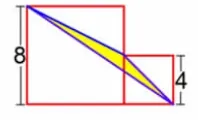
图3

图4

图5

第二，技术的使用启发了学生的想象力。

技术服务于教学，技术提升了教学。王静文老师的课件，不是一种点缀，不仅止于新奇、绚丽，还站在数学学科的本位，挖掘了几何解题的动态角度，很好地启发和支持了学生在平行线上寻找动点，构建等高（等积）三角形的想象，把传统的“难题”“难讲清楚的题”转化成了“巧题”“可以看明白的题”。

教学设计千万条，内容形式并两条。选择好的数学问题，利用好现代技术，我们能为儿童创造更多更好的学习机会，带来更多更好的学习收获！