基于CRITIC-有限区间云模型的边坡稳定性评价*
王加闯,黄明健,2,过 江
(1.中南大学 资源与安全工程学院,湖南 长沙 410083; 2. 湖南涟邵建工(集团)有限责任公司,湖南 长沙 410011)
0 引言
近几年基建设施规模日益完善,边坡稳定性成为建设过程中比较重要的一环,其稳定性评价成为决定工程施工成败的重要因素。影响边坡稳定性的因素的不确定性、危险性等级分级标准的不确定性以及影响因子权系数求取的不确定性,这些使得边坡的稳定性等级分类和工程治理充满着不确定性。为此学界专家学者基于这种不确定性问题提出了多种理论来探讨边坡的稳定性。
宋盛渊等[1]利用突变理论模型剖析了边坡系统的内在机制;胡军等[2]提出了BP神经网络的耦合模型;戴兴国[3]、闫长斌[4]构建了边坡稳定性评价的距离判别赋权模型,弥补了马氏距离法忽略指标重要性存在差异的缺陷;杨文东等[5]根据指标隶属不同稳定性等级的特征建立了岩质边坡稳定性的云模型评估方法;赵军等[6]基于实际评价指标的综合信息量,提出基于改进的熵权计算权重方法的云模型评价模型。这些理论和模型在一定程度上完善了边坡稳定性的评价体系,但由于影响边坡稳定性因素的复杂性,仍难以克服自身存在的缺陷:突变理论模糊数学模型没有考虑指标权重,只是衡量了指标的相对重要性,仍然掺杂着人为主观性;可拓模型仍采用了主观赋值权重的方法,在计算过程中会忽略一些重要的约束条件;耦合的神经网络算法计算复杂,获取的样本代表性不强,拟合速度难以控制;距离判别赋权模型对样本数据依赖性强。
本文引用结合实际评价指标服从均匀分布和正态分布的有限区域云模型[7]。传统的云模型在边界为单边区间时即形如[0,C]或[C,)区间时,其边缘的指标分布仍如传统正态分布一样,这种理论下的模拟结果,往往会和实际情况存在偏差,因此引入了有限区间的云模型;运用CRITIC算法[8]计算指标权重,可以考虑各指标间的相关性,使计算结果更具有准确性。
1 云模型理论
云模型是由李德毅等[9]提出的一种处理模糊问题的概念模型,其是从隶属度的角度出发处理数据的模糊性和随机性。现已应用于生产生活的多个领域,并取得了良好的效果[10-11]。
1.1 云的基本概念
云模型是利用3个数学符号表示的不确定关系,进而进行定性与定量转化的一种模糊模型[9]。传统的云模型通常处理的是指标分布近似趋于正态分布,但在工程实践中,传统的正态云模型很难正确的描述出模拟对象的特征,故本文采用经修改的有限区间下的云模型。
设U是一个精确数值表示的定量集合,其中,U={x},C是U上的定性概念,若存在任意的定量元素,且x存在1个稳定倾向的随机数μ(x)=(0,1)在定性概念C上的1次随机实现,其中[12]:
μ:U→[0,1],∀x∈U,x→μ(x)
(1)
则x在集合U上的分布称为云,每1个点(x,μ(x))称为1个云滴。
1.2 数字特征
通常云模型概念的支撑,主要用3个基本云模型数字特征值加以表述,即期望Ex、熵En、超熵He[9]。期望Ex代表了定性概念的中间位置,决定了云滴分布的位置;熵En表示在论域区间被定性概念表述的云滴的取值范围,反映了基本概念的模糊性和随机性;超熵He,也就是熵的熵,表示熵的不确定性,在云图中,通常表示云的厚度,超熵越大,云越厚。
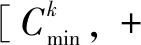
(2)
(3)
(4)
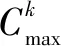
(5)
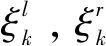
(6)
(7)
同理亦可求出指标值越大,等级区间越小型指标属于等级k的左、右半区间长度:
(8)
(9)
1.3 云发生器
正向云发生器是云模型从理论到实际应用的关键,是利用云特征参数N(Ex,En,He)产生云滴即P(xi,μi)(i=1,2,3,…,n),进而将定性分析向定量计算的转化过程;以正向云发生器为载体,利用云模型特征参数,结合指标等级特征和想要生成的云滴数N(本文取N=5 000),通过Matlab编程即可进行拟合。当指标处于两端等级云均值之间的区间里时,该数学概念模型可以有如下定义:设U是1个精确数值表示的定量集合,其中,U={x},C是U上的定性概念,存在任意的定量元素x,且x存在1个稳定倾向的随机数μ(x)=[0,1]在定性概念C上的1次随机实现。若x满足:x~[Ex,En2],x服从在特定有限区间里的正态分布,即x对C的确定度满足:
(10)
当指标远离期望Ex,此时x服从确定度为1的均匀分布。综上所述,x服从的分布为式(11),本文kmax=5:
(11)

2 有限区域云模型和改进CRITIC法赋权模型的构建
所谓权重,是指在评价过程中,影响问题因素的重要程度,这种重要程度可以通过定性概念描述,也可以用定量数值表示。定性描述的权重充满着主观性,因此在实际生产中的指标权重,通常会用具体的算法表示。传统求权算法通常只考虑指标信息量大小忽略了指标的相关性,因此本文主要采用另一种客观赋权法—CRITIC算法[8]。
2.1 边坡稳定性评价计算框架及流程
1)根据众多学者和地质研究人员的边坡稳定性分析工作,建立滑坡评价指标的危险性等级划分标准;2)求出分类指标的云特征参数利用云发生器绘制云滴图,生成云模型;3)根据样本实测数据计算各指标对应的各级别确定度;4)利用改进的CRITIC算法计算各指标权重;5)计算综合权重值,按照最大隶属度原则确定边坡危险等级。
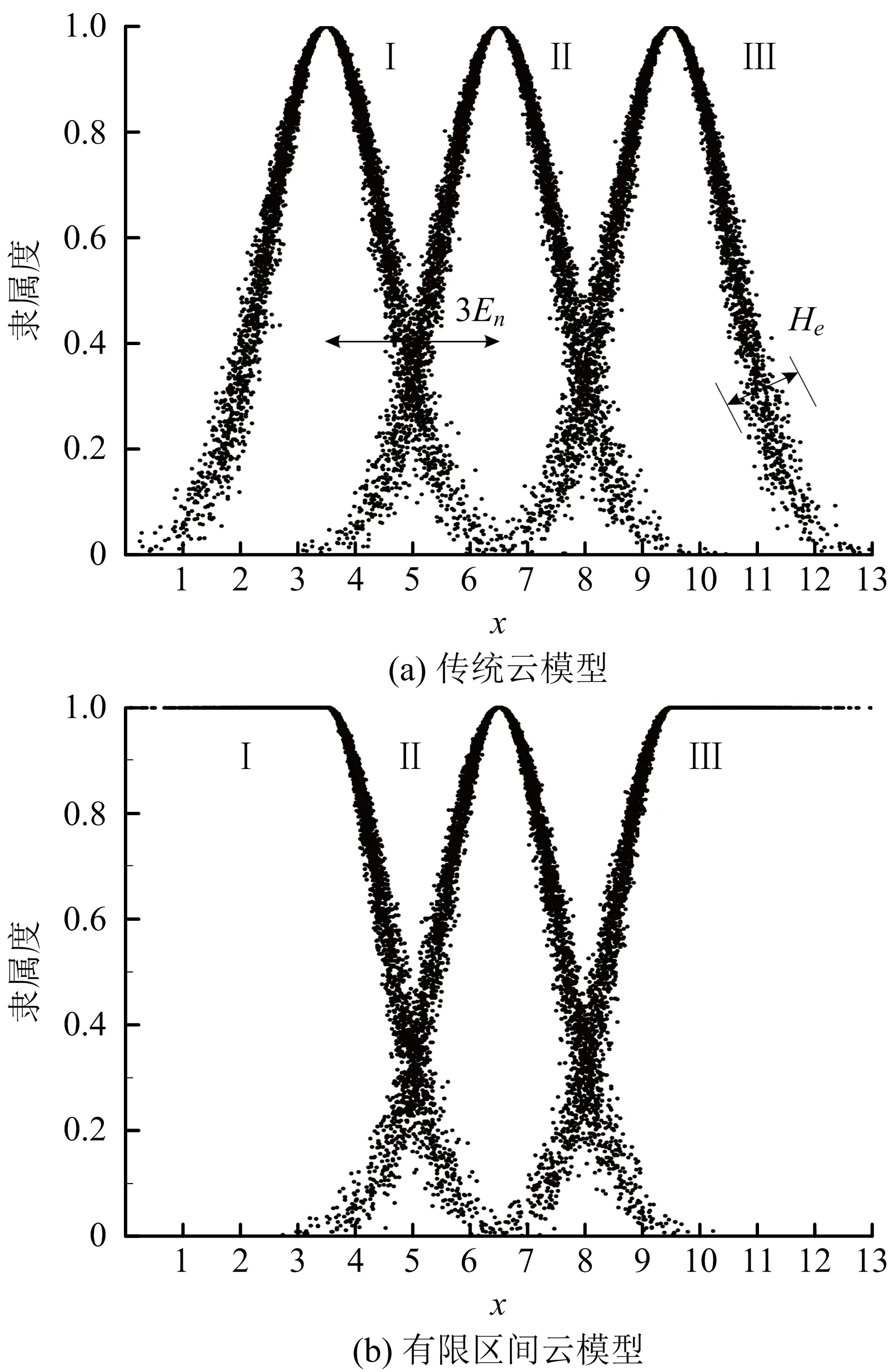
图1 传统云模型与有限区间云模型Fig.1 Traditional cloud model and finite interval cloud model
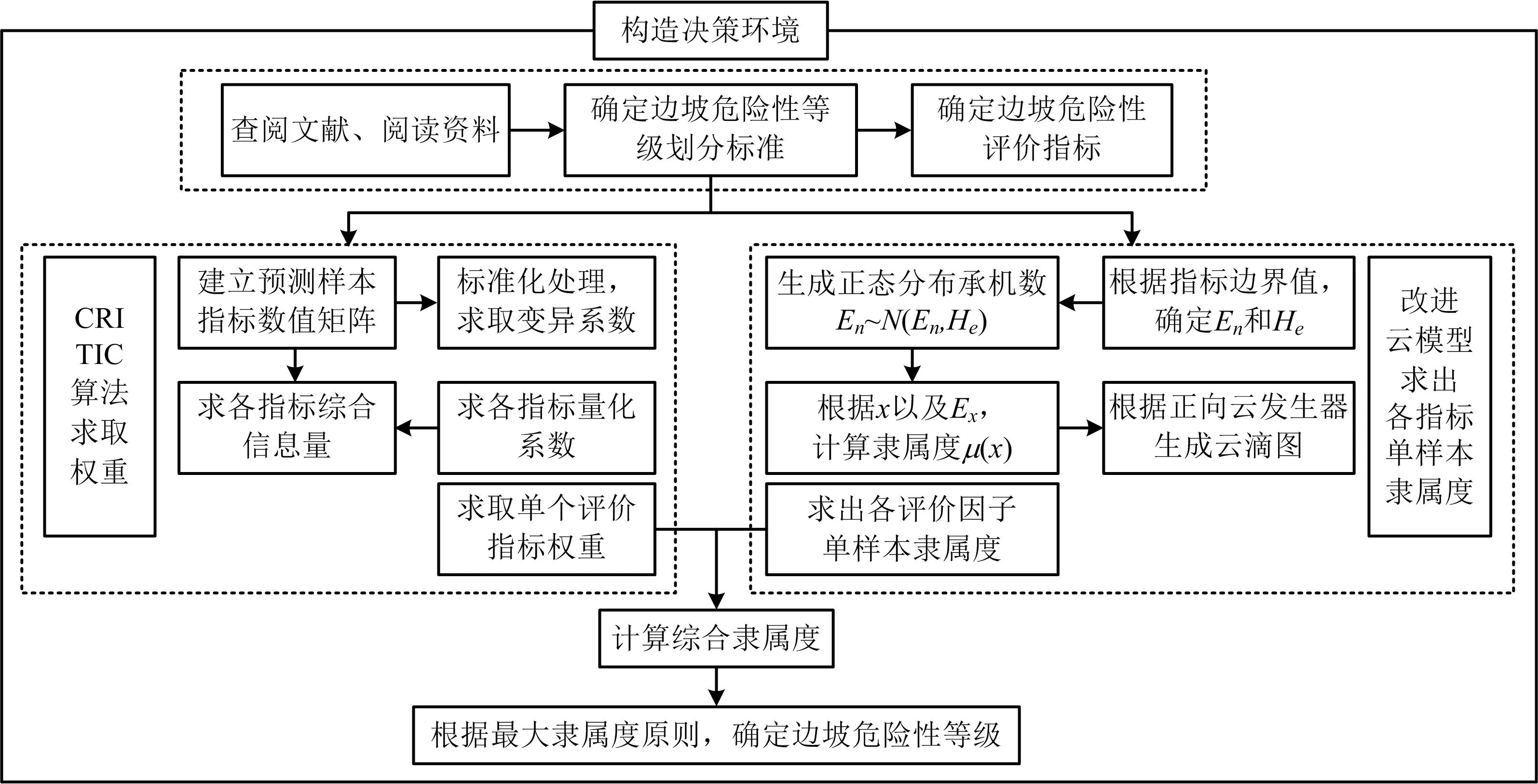
图2 边坡稳定性评价流程Fig.2 Procedure of slope stability evaluation stability evaluation flow chart
2.2 CRITIC法赋权算法
CRITIC算法是由Diakoulaki[15]在1995年提出的一种客观赋值法。这种方法通常用以下2个量来反映:指标间的相关系数及指标内的变异大小。通常相关系数越大,指标间的冲突性越小,体现的信息量重复性越强,指标所占权重也就越小;指标内的变异大小,通常用指标变异性进行量化,用指标的标准差来衡量,标准差越大,对象之间的差异就越大,指标所占权重就越大。
基于以上2个量,不难看出,基于CRITIC算法所得到的权重大小,既考虑了评价指标间的相关性,又考虑了评价指标内的变异性,即体现的信息量,因此,优越于信息熵算法只考虑指标信息量大小,所得权重也更加准确、客观。设评价对象m个,评价指标n个,其主要步骤如下[9]:
1)利用初始数据,建立预测样本指标数值矩阵:
X=(xij)m×n
(12)
式中:xij为第i个评价对象第j个指标所对应的原始数值。
2)根据Z-score方法,对式(12)矩阵X中的指标值进行标准化处理:
(13)
根据该算法,上述公式中2个参数:
(14)
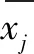
3)求指标的变异系数:
(15)
式中:vj为第j个指标的变异系数。
4)利用步骤2)得到标准化矩阵X*,利用统计学概念计算相关系数,得到相关系数矩阵:
R=(rkl)n×n,k=1,2,…,n;l=1,2,…,n
(16)
式中:rkl为第K个指标和第l个指标间的相关系数。
5)求各指标表示独立性程度的概念—量化系数:
(17)
6)计算各指标综合信息量:
(18)
7)确定各评价指标权重:
(19)
2.3 综合权重的确定
经过以上步骤的展开和计算,我们可以得出不同评价指标实测数据x隶属于某云滴确定度μ(x),再结合CRITIC算法算出不同评价指标的权重,则最终的综合确定度公式:
(20)
式中:μk,j为样本的第j个指标的实测值所在k的确定度;ω(Ej)为样本第j个评价指标所占权重大小。
根据最终的综合确定度,按照最大隶属度原则,确定样本的隶属等级:
L=max(μ1,μ2,μ3,…,μk)
(21)
3 工程实例
3.1 评价指标的选取
边坡的稳定性受自身的复杂特点和工程技术的影响,最主要的因素主要包括边坡所在位置的地质地貌、水文结构和外部环境如人类的生产活动、地质灾害、降水量等。到目前为止,决定边坡稳定性的因素,在学界和地质工程界并没有统一标准。根据建立的分级标准应满足代表性、关联性、易量化、易获取和存异性5个原则,参考相关文献[13],特选定单轴抗压强度(Rc)X1、弹性模量(Em)X2、泊松比(μ)X3、岩体结构特征(RQD)X4、岩土黏聚力(C)X5、内摩擦角(φ)X6、日最大降雨量X7、最大地应力X8、地下水状态X9、边坡高度X10、边坡角X11和岩体声波速度X12为评价因子。
由于边坡稳定性影响因素的随机性和模糊性会随着时间和环境的变化而改变。分级标准的基础通常与岩质边坡的实际情况、不连续的地质情况有关。一般情况下,由于工程背景的不同,许多潜在因素也会对实际工况产生影响。结合文献[16]露天采场的实际情况,参照工程岩体分类标准将边坡分为5个等级,分别为极稳定(Ⅰ)、稳定(Ⅱ)、基本稳定(Ⅲ)、不稳定(Ⅳ)和极不稳定(Ⅴ)。具体指标的分类标准见表1,边坡指标实测值见表2。
3.2 云滴图的生成
根据有限区域云模型理论和分级标准,依据式(2)~(9)确定云特征参数,生成云滴图如图3所示。横坐标表示评价指标,纵坐标表示不同取值的评价指标所确定的确定度,即隶属度。
根据2.1节的计算方法,利用改进的CRITIC算法进行计算,根据公式(14)可计算出各指标的均值和方差,同时利用式(15)求出变异系数,根据初始指标的实测值,计算出标准化后数据所对应的指标之间的相关系数,利用式(19)可求出各评价指标的权重,如表3所示。
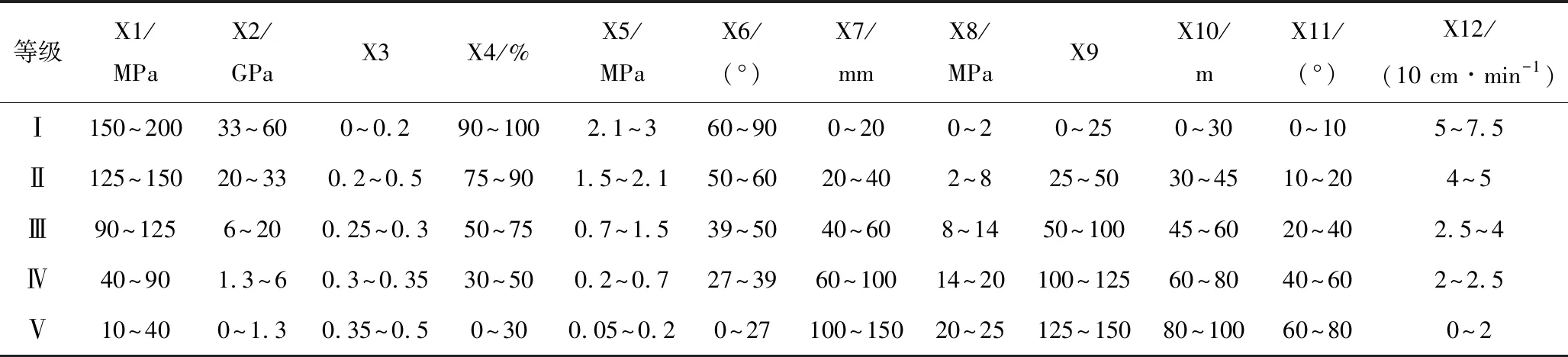
表1 单因素边坡稳定性评价指标Table 1 Single factor evaluation indexes of slope stability

表2 指标实测值Table 2 Measured values of indexes

图3 评价指标隶属于各级别的云滴图Fig.3 Cloud droplet graph of evaluation indexes attaching to each level

评价指标X1/MPaX2/GPaX3X4/%X5/MPaX6/(°)X7/mmX8/MPaX9X10/mX11/(°)X12/(10 cm∙min-1)指标权重0.0500.0690.1400.020.0890.1450.0010.1200.0370.1830.1340.013
3.4 预测结果及分析
基于CRITIC算法和有限区域下云模型的计算模型,根据式(2)~(4)求出的云模型特征参数,进而结合云图和正态云发生器,可计算出实测值隶属于不同级别的隶属度,带入式(20)中,按照最大隶属度原则,可求出不同样本的最终稳定性级别。以第1个样本第1项评价指标为例即单轴抗压强度,实测值为X1=52.6 MPa,根据有限区域云模型计算公式和正向云发生器,可以求出该实测值隶属于不同的评价等级分别为μ1=μ2=0,μ3=0.001,μ4=0.829,μ5=0.006。根据所求确定度数值,单从第1个样本的单轴抗压强度可以得知,该露天矿边坡稳定性隶属于第Ⅳ等级,隶属于第五等级有很小的可能性,有非常小的可能隶属于第Ⅲ等级,但是不可能隶属于Ⅰ,Ⅱ等级,这与事实比较符合。因此可以结合式(20),根据最大隶属度原则,计算出不同边坡所在的危险等级,分级结果及对比见表4。
根据最终权重结果和确定度分析,相对于其他方法[16],基于CRITIC算法的有限区域云模型方法相对保守。样本1,3,4危险性等级处于第Ⅲ等级,即基本稳定状态,但是样本1和样本4对于等级Ⅳ有一定的倾向性,可以对边坡的治理和防护提供一定的参考;样本2根据最大隶属度原则,该样本危险性处在第Ⅳ等级,即不稳定状态,根据实测数据可知,相对于其他样本,样本2的X6(内摩擦角)因素较大,而且根据权重计算,该影响因素所占权重较大,因此对边坡的稳定性有一定的影响。对于不稳定样本和有不稳定倾向的样本应该采取一定的防护措施,如使用锚索和喷射混凝土加以牢固,或者利用网格梁支护等措施进行处理,做好边坡稳定性工作的预防工作,防止发生危险事故。

表4 分析结果及比较Table 4 Analysis results and comparison
4 结论
1)利用CRITIC算法计算权重,选取某铜矿山露天边坡,经对实测数据关联度的计算,提高了评价指标权重的准确性。根据最终评价结果分析,利用该算法不仅可以进行安全现状评价,也可以在得到危险性等级的同时,了解样本危险性等级的倾向性,达到安全预测的目的。
2)针对边坡稳定性评价的不确定性,选取某铜矿山露天边矿的4个剖面,着重选取了12个影响边坡稳定性的不安全因素(评价指标),使得评价结果更为合理,评价指标体系更加完善,提高了评价的可信度。
3)根据传统正态云模型,结合改进的有限区域云模型,使评价指标的隶属度更加合理准确,弥补了传统模型下理论分布与实际部分不符的情况,摆脱了传统理论模型下模拟结果可能超出实际范围的风险;同时结合CRITIC求权算法,使得模拟结果与实际情况更加符合。结合多种分析方法可知,该方法预测结果相对准确,对分析露天矿边坡稳定性问题提供了可行的定量分析方法。

