高精度非接触磁浮机构电磁干扰特性分析

谢进进，刘 胜，胡 晓，赵艳彬，赵洪波，邱 扬

(1. 上海卫星工程研究所，上海 201109； 2. 西安电子科技大学 机电工程学院，陕西 西安 710071)

0 引言

未来航天技术(如空间科学、高分敏捷遥感等)的发展对卫星平台的控制精度提出了比现有水平超过2个量级的指标需求。双超平台基于“动静隔离，主从协同”的设计理念，采用非接触磁浮机构实现卫星平台的动静隔离设计，将卫星平台设计成空间独立而又有机结合的载荷舱和平台舱两部分，从而使安装活动和挠性部件的平台舱振动和干扰不会传输至载荷舱，空间上达到振动隔离的效果。控制上，双超平台采用载荷舱主动、平台舱从动、两舱协同解耦的控制策略，满足载荷的高性能指标需求。双超平台已成为未来超高指向精度、超高稳定度航天器的理想选择[1-4]。

非接触磁浮机构是双超平台实现“动静隔离非接触，主从协同高精度”的关键执行机构，其输出力精度对双超平台姿态控制精度有重要影响[5]。与传统卫星平台相比，双超平台中新引入的非接触磁浮机构由于采用脉冲宽度调制(PWM)驱动控制来实现对卫星姿态的控制，因此可能会与星上其余单机之间产生电磁兼容问题。PWM驱动方式以往通常应用在感应电机伺服驱动系统中。随着伺服驱动系统中半导体开关器件在工作过程中所产生的电压电流随时间的变化速率越来越快，PWM驱动方式造成的电磁干扰也越来越严重，甚至影响到了整个系统的电磁兼容特性。因此，许多学者开始就PWM控制驱动的电磁干扰及其对系统的电磁影响展开分析研究。例如：WANG等[6]为减少PWM对系统的电磁干扰，提出了新的PWM调制方式；段建东[7]针对感应电机PWM驱动系统所存在的传导干扰进行分析和研究，得到了PWM驱动系统存在的传导干扰时、频域特征；王举贤[8]采用时域模拟实际测试的方法建立了包含PWM逆变器、感应电机和传输线缆在内的系统级传导干扰模型，并通过系统仿真最终得到了共模电磁干扰电压在频域的分布特征。从上述研究中可以看出，PWM电磁干扰会导致很严重的电磁兼容问题。磁浮机构PWM控制信号可能会影响星上其他单机的正常工作，也可能会因受其他单机的影响而降低输出精度，从而使双超卫星姿控精度下降。然而，目前针对卫星平台中的PWM驱动控制系统的电磁干扰问题并未开展深入研究。

本文针对双超平台非接触磁浮机构的PWM驱动控制系统，基于理论方法和仿真分析，分别对PWM控制信号的辐射电磁干扰和传导电磁干扰的时域及频域特性进行研究，并将分析结果与星上其余单机的频率特性进行比对，证实磁浮机构PWM控制信号不会对卫星射频通信设备造成电磁干扰。

1 非接触磁浮机构及其驱动器工作原理

非接触磁浮机构实物如图1所示，其基于洛伦兹力原理产生控制所需的输出力，电涡流位移传感器则用于测量两舱间的相对位置。

图1 磁浮机构实物图Fig.1 Physical map of magnetic device

磁浮机构信息流程如图2所示。磁浮机构中的磁钢提供匀强磁场B。将有效长度为L的线圈放置在磁场B中，当线圈中通入电流I时，线圈会受到水平方向的洛伦兹力F，即

F=(I×B)L

(1)

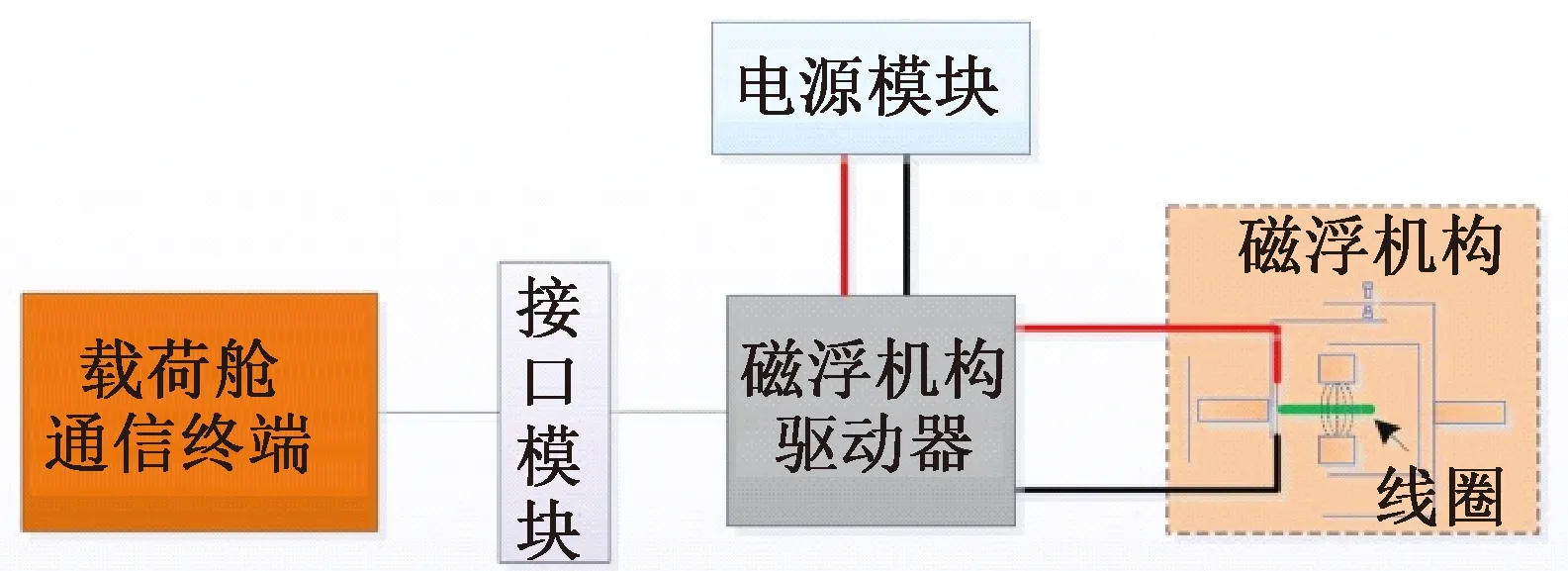
图2 磁浮机构信息流程图Fig.2 Information flowchart of magnetic device

改变线圈电流I的大小和方向，就可实现对洛伦兹力F的控制。由磁浮机构驱动器实现载荷舱通信终端发出的控制电流指令，从而实现磁浮机构对载荷舱姿态及两舱相对位置的控制。

磁浮机构驱动器是磁浮机构产生电磁干扰的主要原因。以PWM开关功放为例进行分析。图3为磁浮机构驱动器主电路的原理图。图中：V1～V4为4个开关管，PWM驱动信号加载在开关管的栅极。当控制信号给V1高电平时，V1导通，同时V3也导通，V2和V4不导通；当控制信号给V1低电平时，V1和V3不导通，V2和V4导通。在驱动器正常工作过程中，开关管V1与V3不断地交替开通和关断，其源极与漏极之间的电压无法瞬时上升和下降，因此，开关管的源极与漏极之间的电压波形是具有短暂上升和下降时间的梯形波。经分析可知，非接触磁浮机构中驱动器的电磁干扰源主要包括PWM控制信号的高频谐波分量、传导电磁干扰等[9-12]。

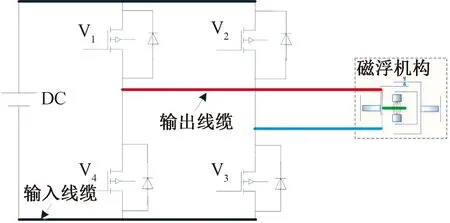
图3 磁浮机构驱动器主电路原理图Fig.3 Schematic diagram of magnetic device driver main circuit

2 驱动器控制信号高频干扰分析

磁浮机构驱动器的PWM控制信号由于自身特征，会产生主要以开关频率为基频的高频干扰。在非接触磁浮机构的工作过程中，激励线圈中会有不同方向的PWM电流信号通过，因此其激励器一般采用H桥电路，如图4所示。线圈可等效为阻抗为Z的元件，Ud为驱动电源电压。H桥电路由4个开关管和4个续流二极管组成，为单电源供电。4个开关管分成2组，V1和V3为一组，V2和V4为另一组，其控制信号为PWM信号。双极性正弦脉宽调制(SPWM)是最为常见的一种PWM信号，下面以双极性SPWM信号控制为例，分析H桥驱动输入输出的时频域特性。

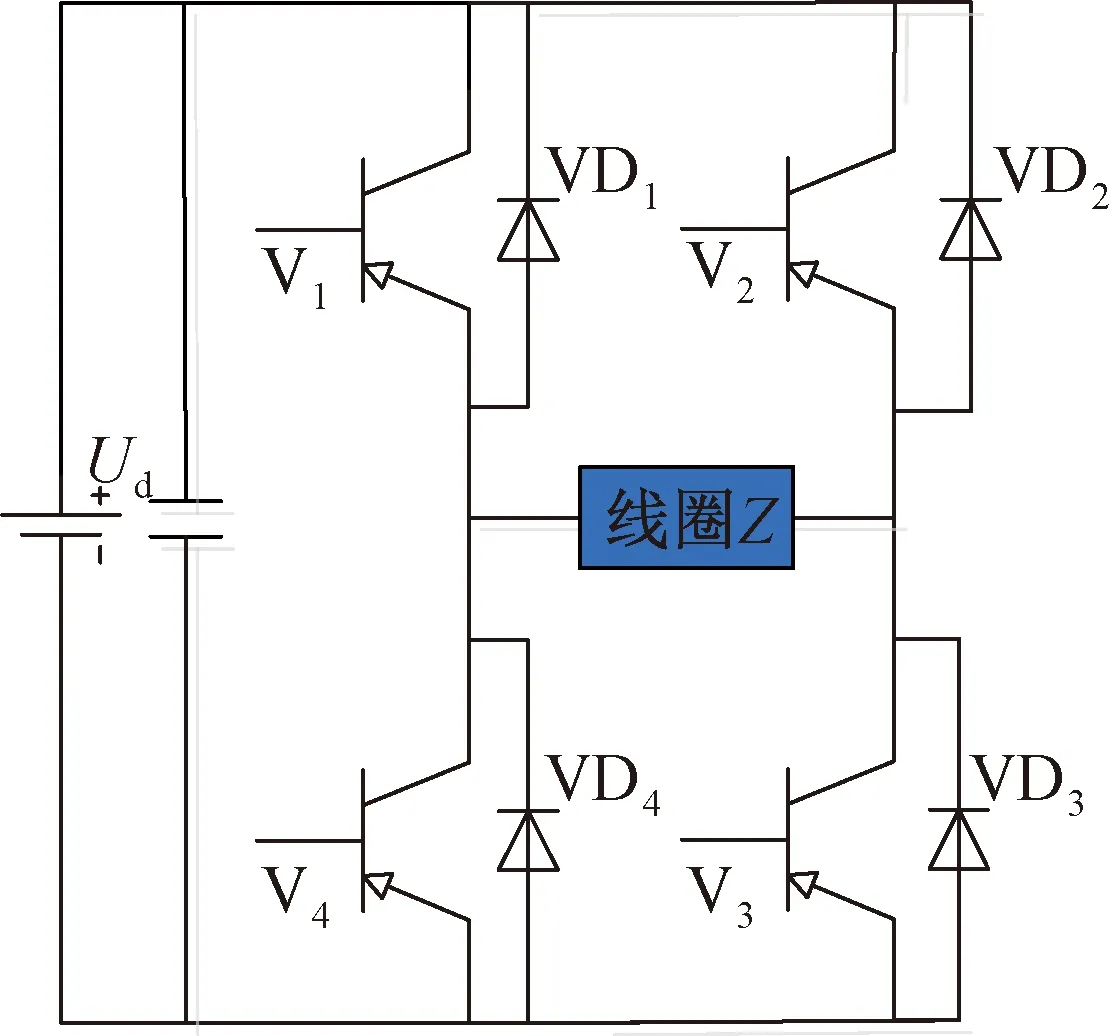
图4 H桥电路示意图Fig.4 Schematic diagram of H-bridge circuit

SPWM是根据面积等效原理，用脉冲宽度按正弦规律变化的PWM波形，即SPWM波形控制电路中开关器件的通断，使其输出的脉冲电压的面积与所希望输出的正弦波在相应区间内的面积相等。以正弦波为调制信号，等腰三角波作为载波，当调制波幅值大于载波幅值时，输出高电平，开关管导通，否则输出低电平，开关管关断，由此得到的就是SPWM波形[13]。

图5为SPWM示意图。设Uo为线圈两端输出电压，Ud为驱动电源电压，Ur为调制波最大电压，ur为调制波信号，ωr为调制波频率，Uc为载波最大电压，uc为载波信号，ωc为载波频率，θ1和θ2为调制波和载波的2个交点，mf为调制比，则有

(2)

图5 SPWM示意图Fig.5 Schematic diagram of SPWM

令调制波信号函数为

ur=Ursin(ωrt+φ)

(3)

式中：φ为初始相位。设载波信号的周期为2π，取一个载波周期，则在一个载波周期中得到的输出电压

(4)

整理可得

(5)

对式(5)进行傅里叶展开，有

(6)

由于输出波形为偶函数，因此有bn=0。

(7)

由式(7)可得

(8)

根据式(8)，只要求解出θ1和θ2，就可得出a0和an的解。图6为SPWM调制中的几何关系示意图，由相似三角形原理，有

(9)

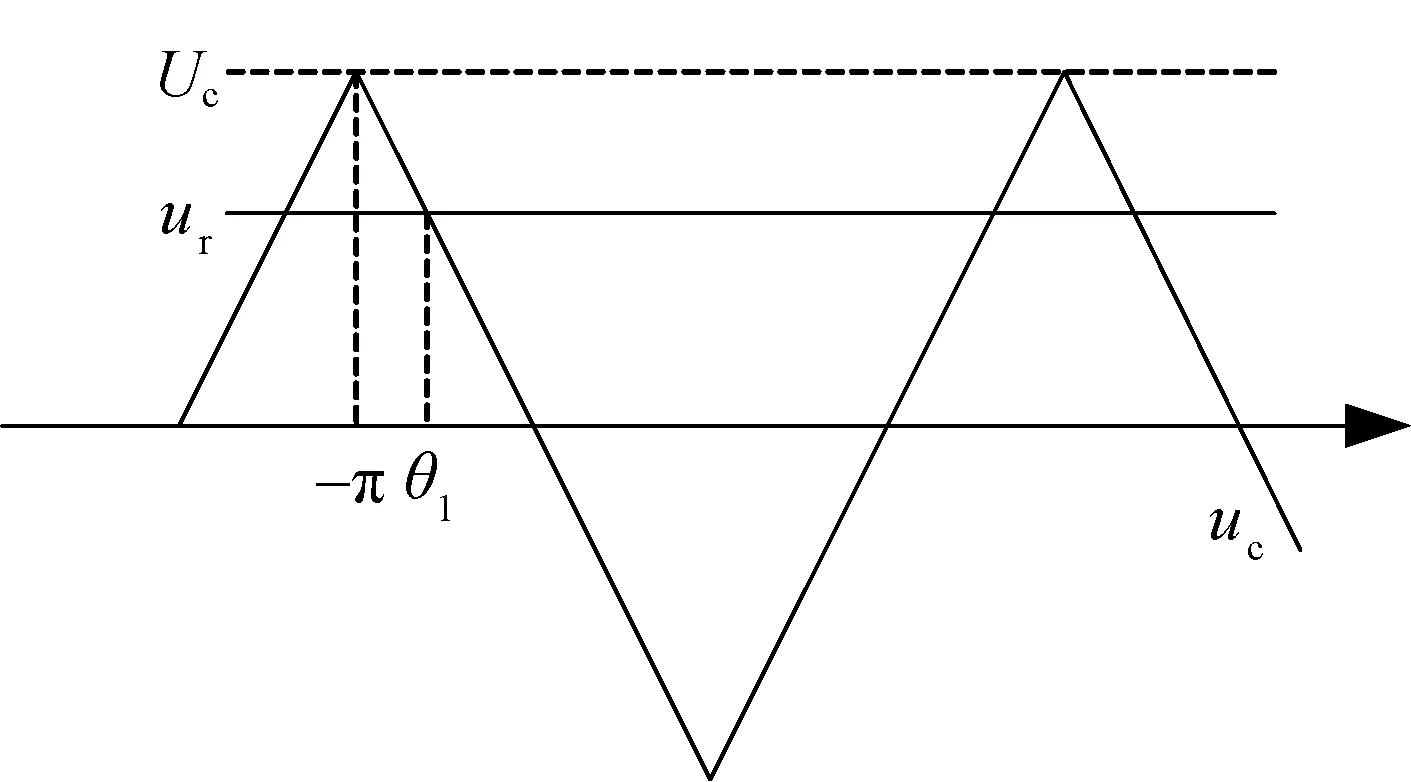
图6 SPWM中几何关系示意图Fig.6 Geometric relationship in SPWM

由此可解得θ1和θ2，即

(10)

从而可得a0和an，即

(11)

由此，SPWM输出电压的傅里叶级数为

n=1,2,…

(12)

可得基波成分为

(13)

令谐波成分为Uoh，即

Uoh=

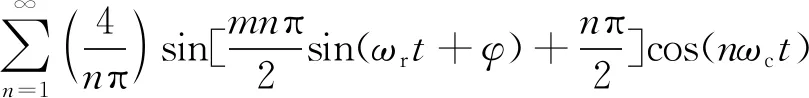
(14)

由贝塞尔公式

(15)

可得Uo的SPWM调制输出电压谐波为

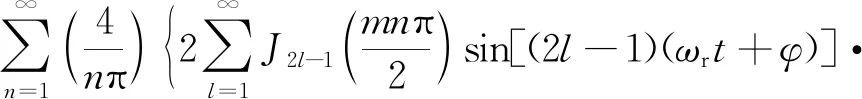
(16)

从式(16)可以看出，线圈两端输出电压中的谐波成分为

(17)

针对控制信号高频干扰展开仿真分析。采用MATLAB/Simulink建立H桥电路，仿真得到其输入输出时频域特性。首先给出负载为纯电阻时的时域波形仿真结果，如图7所示。图中：V1/3和V2/4为开关管对应的控制信号；Idc为直流侧电流；Io和Uo分别为负载端电流和电压。

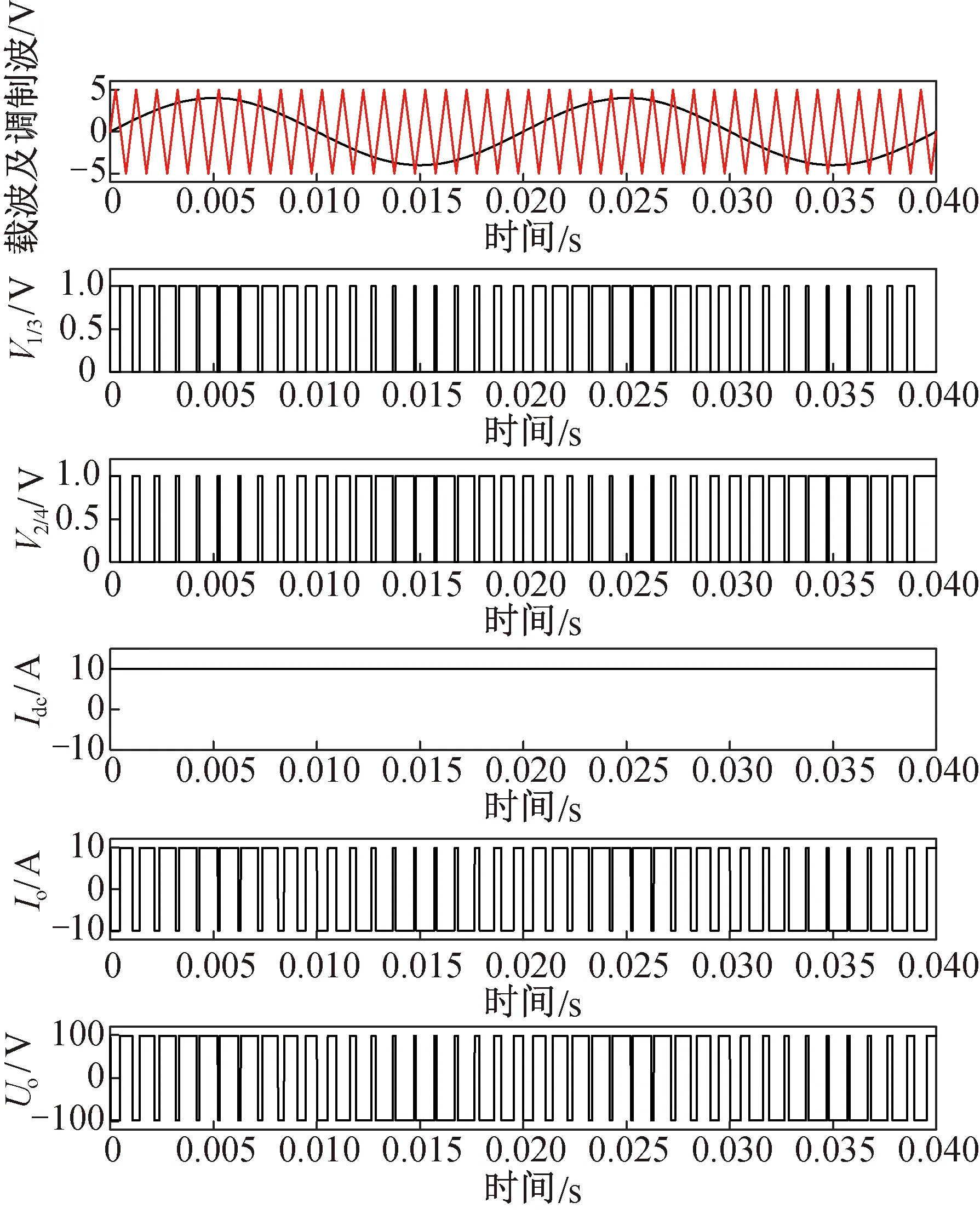
图7 纯电阻负载H桥电路输入输出时域特性Fig.7 Time-domain input-output characteristics of H-bridge circuit with resistive load

从图7可以看出，在SPWM信号的控制下，负载端电压和电流也为SPWM信号，Idc为直流信号，但实际中为防止同一桥臂2个开关管直通，往往会在2路控制信号间加入延迟时间，成为死区时间，即在开关管1和3关断后延迟一段时间后，再让开关管2和4导通，因此在死区时间内，电路电流为零，Idc就变为脉动的直流信号。实际中激励线圈为阻感性负载，负载为阻感性负载时H桥电路的输入输出时域特性如图8所示。

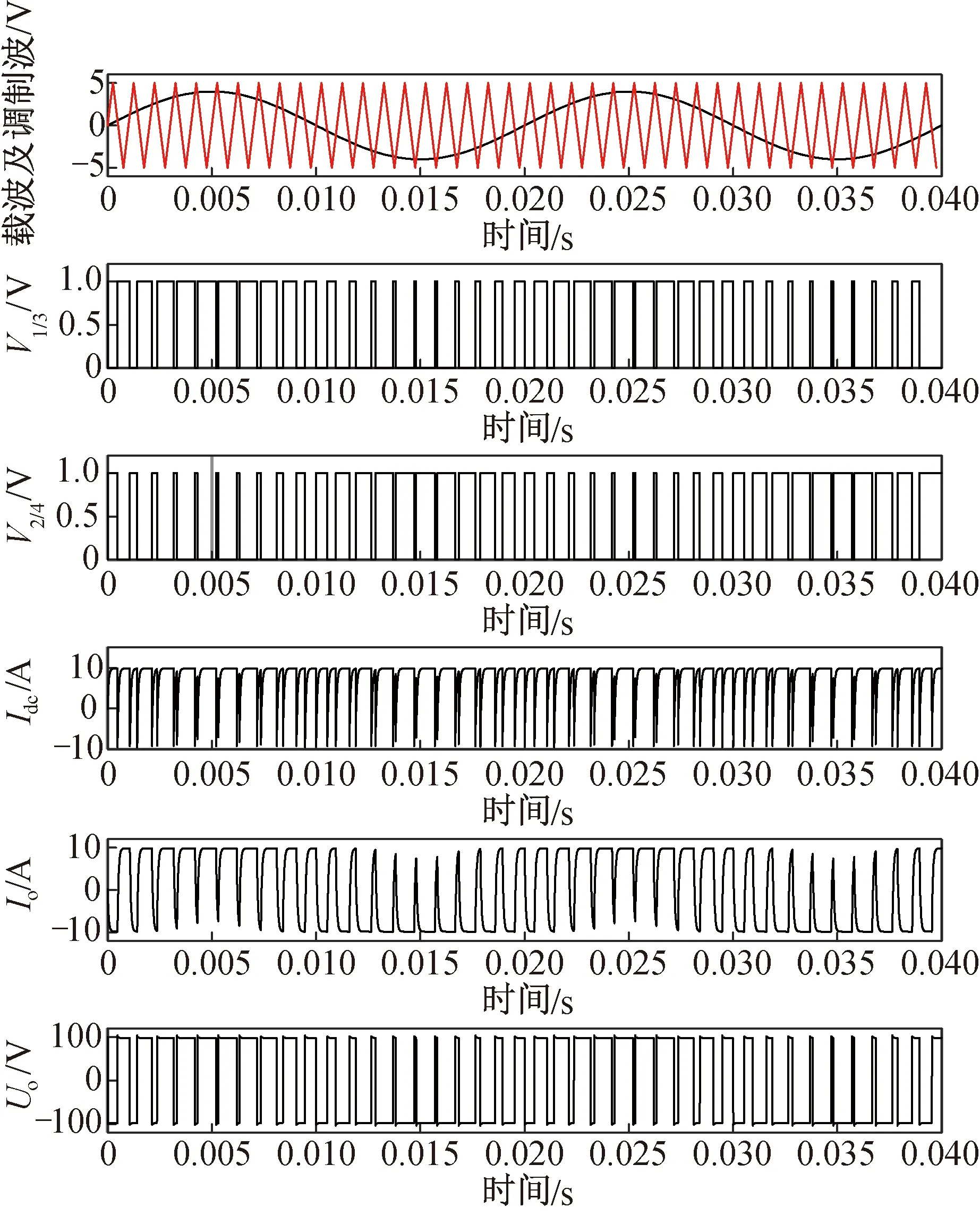
图8 阻感性负载H桥电路输入输出时域特性Fig.8 Time-domain input-output characteristics of H-bridge circuit with resistance inductive load

比较图7，8可发现，Idc和Io波形均发生了变化，尤其是Idc表现为脉动的直流，其原因在于负载电感的储能作用，导致负载电流不能突变，这从Io波形的变化上就可发现。

以开关管V1和V3为例，当其导通时，电流流向如图9(a)所示。当开关管V1和V3由导通状态向关断状态转换时，负载电感的储能作用，使得负载电流不能突变，负载相当于一个电流源，将电感储能通过二极管VD2和VD4续流，其电流流向如图9(b)所示，此时直流侧电流反向，这就是直流侧电流脉动的原因。

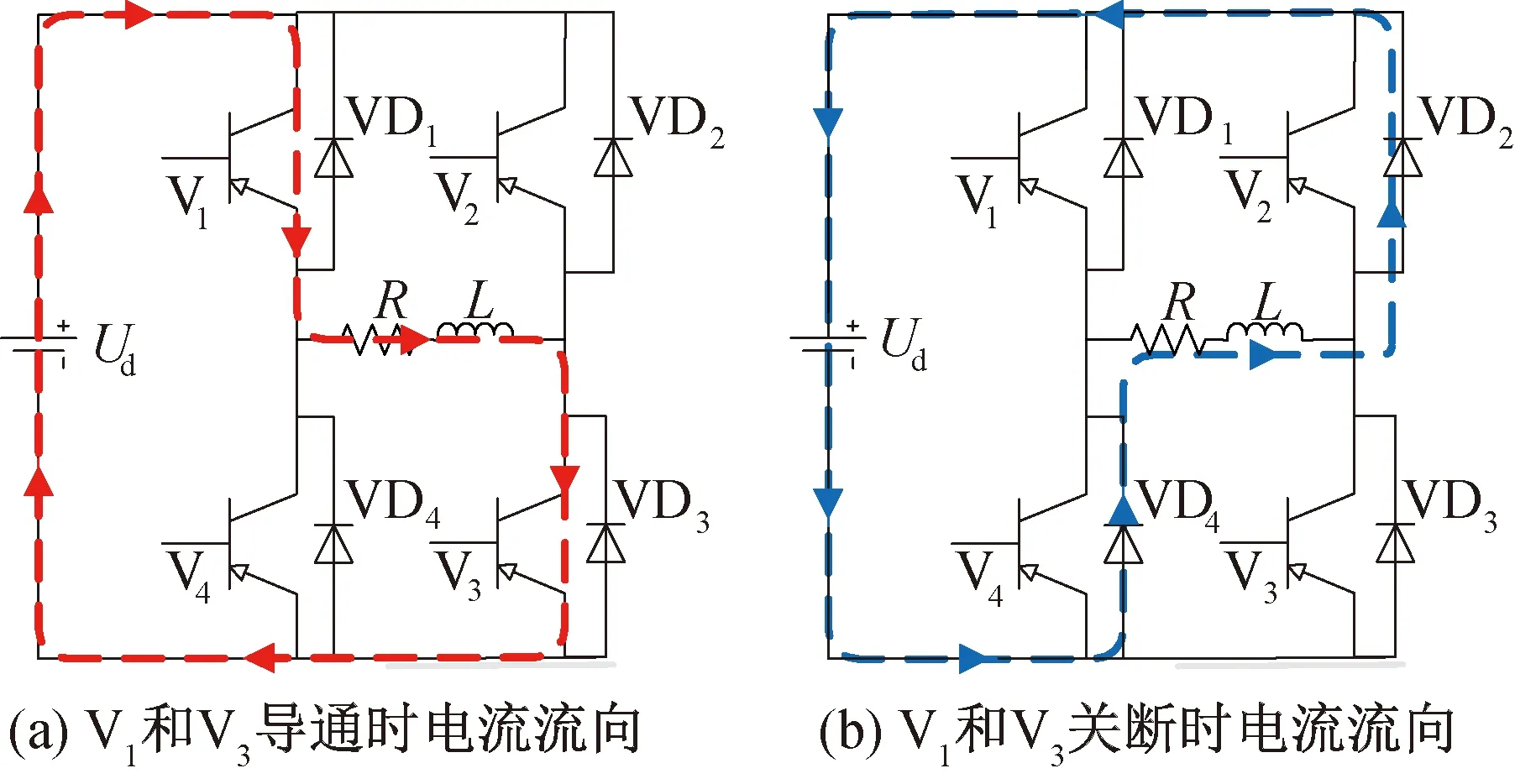
图9 V1和V3导通和关断时电流流通路径Fig.9 Current flow paths during turn-onand turn-off of V1 and V3

以上分析了阻感性负载时H桥电路的输入输出时域特性，下面分析其频域特性。直流侧电流Idc的频谱图如图10所示。仿真中SPWM控制信号的载波信号频率(开关管的开关频率)为750 Hz，调制波信号频率为50 Hz。

图10 直流侧电流Idc频谱图Fig.10 Frequency spectrum of Idc

图11 负载端电压和电流信号的频谱特性Fig.11 Frequency spectrum characteristics ofvoltage and current in load side

从图10可以看出，直流侧除了直流信号外，其频谱中还包含了一些与开关频率和调制波频率有关的谐波信号，可描述为

(18)

图11(a)，11(b)分别为负载端电压和电流信号的频谱特性。从图11可以得出，负载端电压和电流的频谱特性一样，其谐波成分同样与开关频率和调制波频率有关，可描述为

(19)

综合上述分析可知，采用SPWM控制的驱动器会导致电源线和激励线圈上产生一些与开关频率和调制波频率相关的谐波干扰信号。经过分析可知，该类谐波干扰信号的频率与开关管的开关频率相关，开关频率越高，谐波干扰频率就越高。由于一般开关频率可达数百千赫兹，因此谐波干扰频率可达百兆赫兹。

3 驱动器传导电磁干扰分析

在磁浮机构驱动器中，理想的驱动PWM波形是方波，但实际的开关器件开通和关断有一定的时间，并不能输出理想波形。在开关器件工作过程中，会产生电压变化率dV/dt，使得产生的PWM驱动波形近似梯形[14]。在磁浮机构线圈驱动器工作过程中，实际电压脉冲波形的上升沿与下降沿是非线性的，不便于直接对其进行频谱研究，因此用理想的梯形波形来近似模拟电压脉冲波形，即假设上升沿和下降沿是线性的，且上升时间与下降时间相等，如图12所示。图中：VDC为梯形波形幅值电压；T为梯形波周期；tr与tf分别为梯形波上升时间与下降时间，且tr=tf；t0为脉冲波形开始时间，为方便分析，将t0设为0；ton为半幅度值处上升沿与下降沿之间的时间间隔。

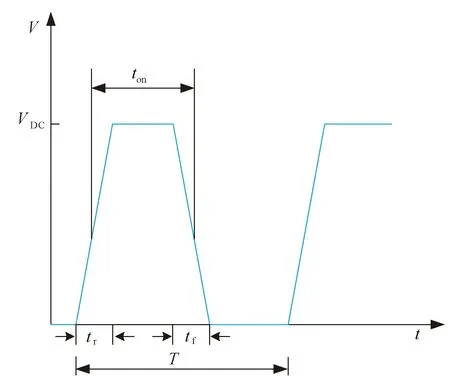
图12 梯形脉冲波形示意图Fig.12 Schematic diagram of trapezoidal pulse waveform

则理想梯形波的时域表达式为

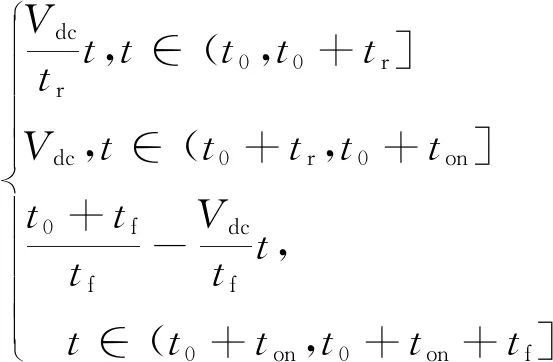
(20)

将式(20)经傅里叶变换，得到电压V(t)的幅频特性，即

(21)

图13 dV/dt梯形波的幅频特性Fig.13 Amplitude-frequency characteristics of dV/dt trapezoidal waves

梯形波产生电压变化率dV/dt时，电压频谱特性仿真分析如图13所示。从图13可以看出，当频率达到100 MHz时，电压幅值已接近10-5V，即频率到100 MHz时干扰电压已衰减到极小的值，可见传导电磁干扰频率最高为100 MHz。

4 与星上其他单机对比

由以上分析可知磁浮机构驱动器控制信号无论是高频辐射干扰还是传导电磁干扰，其干扰频率范围均可达到100 MHz。高频辐射干扰会对无线设备通信产生干扰，而传导电磁干扰则会通过传输电缆间的相互耦合对电缆上的传输信号造成干扰。因此，需要对卫星上的通信设备的频谱进行分析，以判断磁浮机构驱动控制信号是否会对平台设备造成干扰。

通过对卫星平台的系统组成进行分析，卫星平台可能受到电磁干扰的主要通信设备包括USB应答机、测控设备、GPS接收机、数传设备等。这些单机的通信频率与非接触磁浮机构控制信号高频干扰和传导电磁干扰的频率覆盖如图14所示。

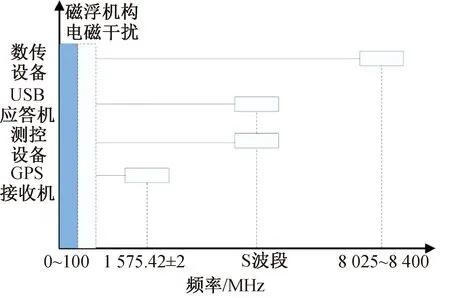
图14 有效载荷和PWM信号频谱Fig.14 Frequency spectrum ofpayload and PWM signals

从图14可以看出，非接触磁浮机构驱动器控制信号高频辐射干扰及传导电磁干扰频率与GPS、测控、数传等高频无线通信相差较大，对这些设备产生的电磁干扰很小。

5 结论

本文主要研究了双超平台的姿控关键执行机构非接触磁浮机构的电磁干扰特性，介绍了磁浮机构及其驱动器工作原理，分别针对驱动器PWM控制信号产生的高频干扰和传导电磁干扰特性开展了理论和仿真分析，并将其频率特性与星上其他典型单机的工作频率特性进行了比对。通过对比分析可以看出非接触磁浮机构干扰信号的频率与星上其他典型单机之间的频率间隔较大，相互之间产生的电磁干扰可忽略。在后续研究中，将进一步分析磁浮机构PWM控制干扰信号对星上各类传输线缆的电磁耦合问题，为非接触磁浮机构及双超平台早日在轨应用奠定基础。