缫丝机卷绕机构参数优化及其试验验证

周 贤， 王 英， 陈建能， 汪 锐， 陶德华

(1. 宁波大学 机械工程与力学学院， 浙江 宁波 315211；2. 浙江理工大学 机械与自动控制学院， 浙江 杭州 310018)

缫丝机缫制生丝过程中，卷绕运动是核心运动，生丝被卷绕成一定形状的卷装，为后续工序做好准备[1-3]。随着我国纺织行业的产业升级，高速、大卷装卷绕的缫丝机已成为发展趋势。卷绕运动由小䈅的回转运动和络交机构的往复运动组成，小䈅回转卷取丝线，络交机构带动丝线做往复直线运动，使卷绕于小䈅上的丝线形成网状丝片，并最终形成具有一定厚度的卷装[3-4]。卷绕运动直接影响卷装的成形质量，进而影响缫丝效率和缫丝机的可靠性。

保证生丝卷绕工艺的传统方法是“等速络交”，即络交杆匀速往复运动。在该理论下设计的卷绕机构根据结构形式分为2类：双圆柱凸轮式[5]和周转轮系式[6-7]。双圆柱凸轮式可通过改变圆柱凸轮工作廓线来实现络交杆匀速往复运动，但当络交杆匀速往复运动时，因换向时冲击大，不能适应高速和大卷装缫丝；周转轮系式运用1对偏心圆齿轮的非匀速传动来改善络交杆往复速度的均匀性，该类机构运动较平稳，能适应高速和大卷装缫丝，但络交杆往复运动过程中速度变化较大，不能很好实现等速或近似等速运动，形成的丝片中间凹、两边凸，不利于丝片成形稳定和丝片厚度的增加。同时，为使络交杆往复运动规律一致，还需要再经过齿数比为 1∶2 的圆柱齿轮副的传动，即需采用两级齿轮传动，但存在传动路线长、效率低、结构复杂等缺点，且双偏心圆齿轮副啮合时存在较大齿侧间隙[8]，降低了整套机构运动的平稳性。

针对以上问题，钱永年等[9]提出了应用椭圆齿轮非匀速传动的卷绕机构，在改善络交杆往复速度均匀性的基础上，避免了齿侧间隙较大问题。在此基础上，Wang等[10]提出应用混合阶数偏心共轭非圆齿轮副来设计卷绕机构，即采用一阶偏心圆齿轮及与其共轭的二阶非圆齿轮组成的齿轮副，无需再经过齿数比为1∶2的圆柱齿轮副的传动，避免了传动路线过长的问题。除混合阶数偏心圆类非圆齿轮副，常用的混合阶数非圆齿轮副还有椭圆类、巴斯噶蜗线类、正弦类和傅里叶类，本文运用这5类混合阶数非圆齿轮副对周转轮系式卷绕机构进行设计，得到5种不同类型的应用非圆齿轮传动的卷绕机构。不同类型的非圆齿轮传动，对应的运动规律不同，即使同一类型非圆齿轮传动，当节曲线参数变化时，运动规律也发生变化，并且非圆齿轮节曲线参数较多，例如偏心圆类，其节曲线参数包括偏心圆半径、偏心距和变性系数[11]。为实现多参数的非圆齿轮节曲线设计，通常是根据传动要求建立运动学方程并编写辅助分析程序，通过人机交互的方式对节曲线参数进行优选[10]，但该方法要求用户对相关领域的认知程度高，且需多次重复试凑才能得到满意的机构参数。为能根据实际缫丝作业要求方便快捷得到满足生丝卷绕工艺的非圆齿轮节曲线参数，本文建立了5种卷绕机构通用参数优化数学模型，进而进行实例优化求解，并对优化结果进行试验研究。该优化模型的建立和求解为卷绕机构的参数优化提供了一种有效方法。

1 生丝卷绕运动

1.1 生丝卷绕原理及规律

缫丝机工作过程中生丝的卷绕运动如图1所示。小䈅以转速n0回转，丝线在卷取点P被小䈅卷取，同时丝线在A点由络交机构的络交杆带动以线速度vH作往复运动，丝线以螺旋线的规律卷绕在小䈅上。每次往复，卷绕在小䈅上的丝圈就形成一个丝层面，若干次往复以后，丝层面层层相覆，最终形成具有一定厚度的卷装。为提高卷装成形质量，自动缫丝机络交杆的运动为复合运动，即络交杆在始终点A1和A2的位置沿运动方向发生周期性变化，如图2所示。络交杆往复一次位移为H1，但在往复运动中，起始点A1的位置沿运动方向不断变化，相对应的终点A2的位置也发生变化，A1和A2位置变化的最大值为H3，那么络交杆移动范围H2为H1与H3之和。此复合运动下，当络交杆匀速往复时，卷装断面形状理论上为梯形，能防止塌边、紊乱、脱圈等现象，利于丝片成形稳定，并能减少丝条重叠的几率[2-4]。

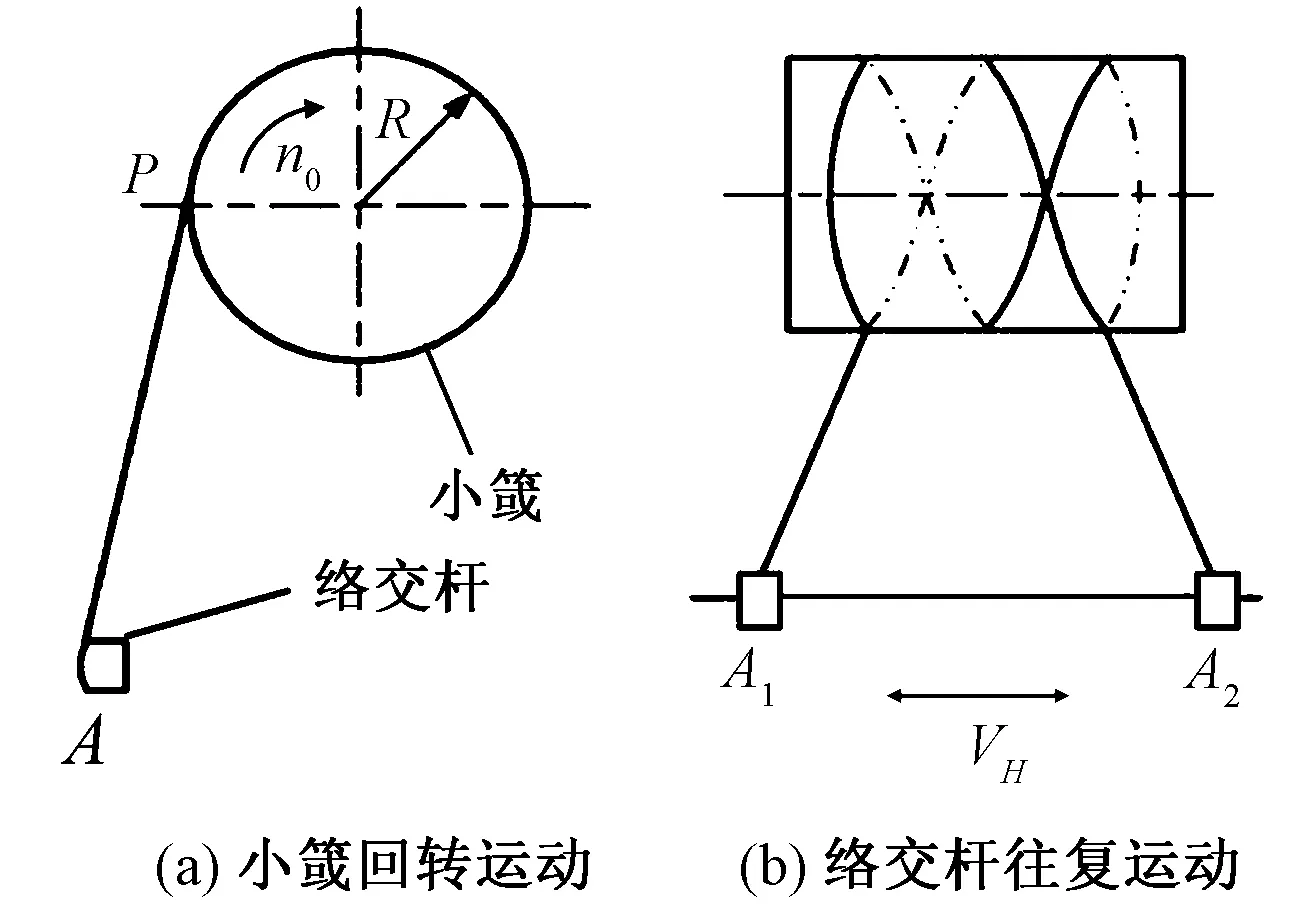
图1 生丝卷绕运动

Fig.1 Winding motion of raw silk. (a) Swing motion; (b) Reciprocating motion

图2 络交杆复合运动

Fig.2 Compound movement of traverse rod

1.2 卷绕机构的工作原理

缫丝机卷绕机构如图3所示。动力由主轴4输入，一方面由链轮3、17及齿轮18、19将动力转递给小䈅轴，带动小䈅匀速转动；另一方面经过一对锥齿轮1、9，再经过主动一阶非圆齿轮及其从动二阶共轭非圆齿轮使曲柄转动，通过连杆、摆杆及推杆使络交杆作周期性的往复运动，同时蜗杆2、蜗轮5将动力传递给共轭凸轮，使叉形摆杆及行星架8往复摆动，从而使从动二阶共轭非圆齿轮转动中心位置发生周期性的变化，最终形成络交杆始终点位置沿运动方向周期性变化，即形成复式络交运动。

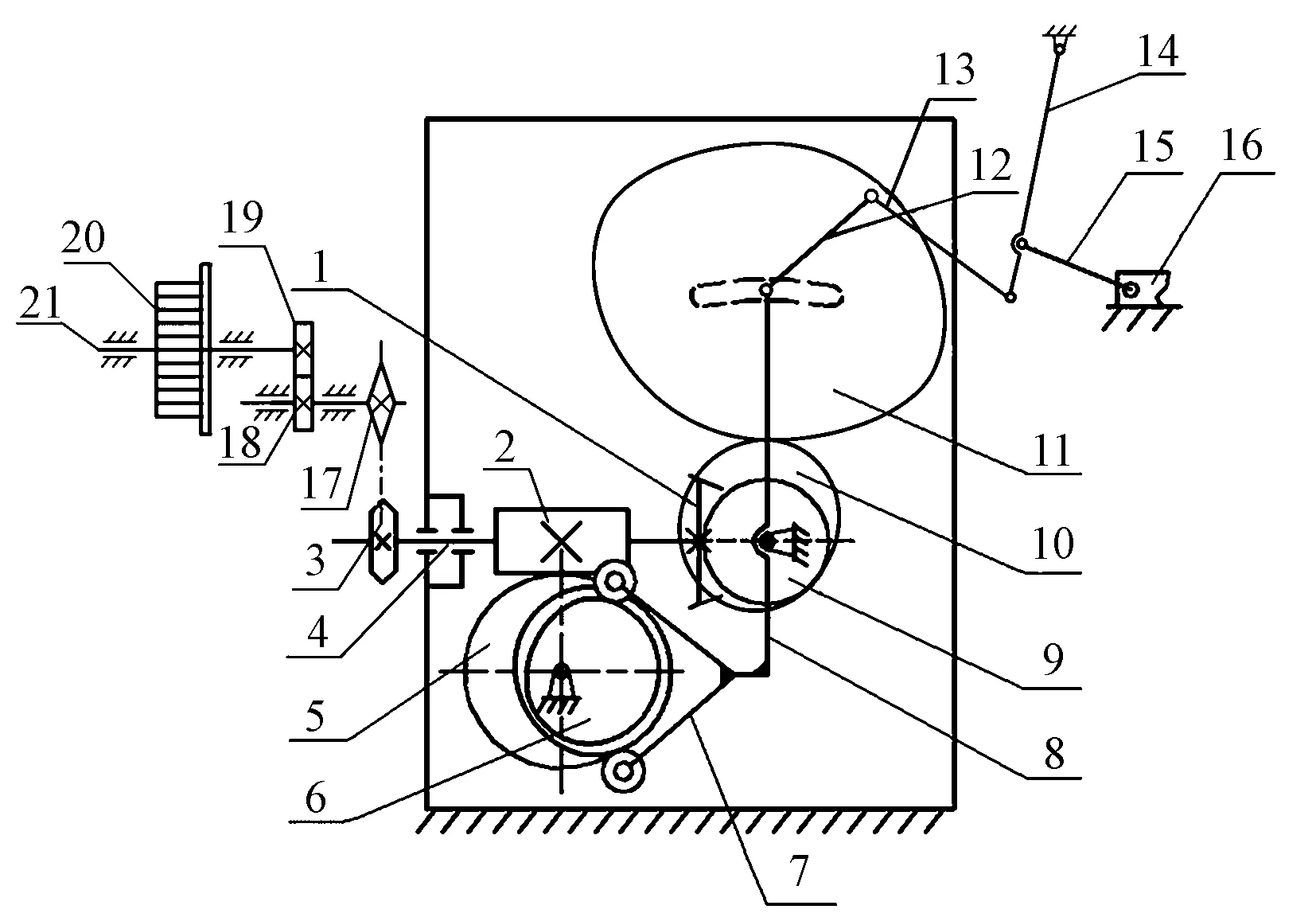
1—主动锥齿轮；2—蜗杆；3—主动链轮；4—主轴；5—蜗轮；6—共轭凸轮；7—叉形摆杆；8—行星架；9—从动锥齿轮；10—一阶主动非圆齿轮；11—二阶从动非圆齿轮；12—曲柄；13—连杆；14—摆杆；15—推杆；16—络交杆；17—从动链轮；18—主动齿轮；19—从动齿轮；20—小䈅；21—小䈅轴图3 新型卷绕机构简图

Fig.3 Structural diagram of winding implementing mechanism

2 通用运动学数学模型的建立

卷绕机构中非圆齿轮传动部分可选择一阶变性偏心圆齿轮及其二阶共轭非圆齿轮、一阶变性椭圆齿轮及其二阶共轭非圆齿轮、一阶变性巴斯噶蜗线齿轮及其二阶共轭非圆齿轮、一阶变性正弦齿轮及其二阶共轭非圆齿轮和一阶变性傅里叶级数齿轮及其二阶共轭非圆齿轮5类常见非圆齿轮副。为方便不同类型齿轮副间的转换计算，建立该类型卷绕机构的通用数学模型是必要的。

2.1 非圆齿轮副节曲线方程的建立

图4示出一阶非圆齿轮及其二阶共轭非圆齿轮传动示意图。当节曲线向径为r1(mm)的一阶主动非圆齿轮匀速顺时针转动角度φ1(rad)时，节曲线向径为r2(mm)的从动二阶共轭非圆齿轮逆时针变速转动角度φ2(rad)。

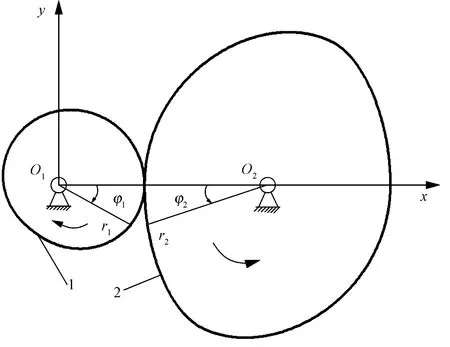
图4 一阶非圆齿轮及其二阶共轭非圆齿轮

Fig.4 First order non-circular gear and second-order conjugate non-circular gear

2.1.1 一阶变性主动非圆齿轮节曲线方程

一阶变性偏心圆齿轮节曲线[11]在一个周期内数学模型可表示为：

(1)

式中：R为偏心圆半径，mm；e为偏心距，mm；m11、m12为变性系数，m12=m11/(2m11-1)。

一阶变性椭圆齿轮节曲线[12]在一个周期内数学模型可表示为：

(2)

式中：A为椭圆的长轴半径，mm；k为椭圆的偏心率。

一阶变性巴斯噶蜗线型齿轮节曲线[13]在一个周期内数学模型可表示为：

(3)

式中：b为发生圆直径，mm；l为其展长，mm。

一阶变性正弦型齿轮节曲线[14]在一个周期内数学模型可表示为：

(4)

一阶变性傅里叶级数型齿轮节曲线[15]在一个周期内数学模型可表示为：

(5)

式中，a0、a1、b1、a2、b2为傅里叶级数方程参数。

2.1.2 二阶共轭从动非圆齿轮节曲线方程

一阶主动非圆齿轮节曲线通用模型可表示为：

(6)

依据非圆齿轮传动原理[16]，已知主动非圆齿轮节曲线方程表达式为r1和非圆齿轮副中心距为a，mm；可推导出与其共轭的二阶从动非圆齿轮节曲线方程为：

(7)

式中，i12为非圆齿轮副的传动比。

为使设计的机构按照周期性的运动规律运转，采用非圆齿轮副必须可实现连续传动，因此设计的主动非圆齿轮及与其共轭的从动非圆齿轮节曲线必须是封闭的，即主动轮转角为2π(rad)时，对应的二阶共轭从动轮转角为π(rad)，用数学表达式可表示为：

(8)

2.2 络交杆运动学方程的建立

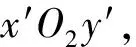
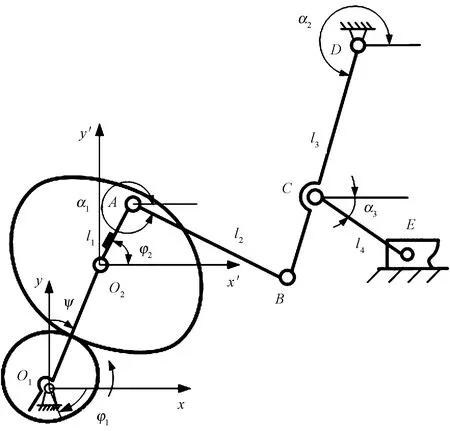
图5 周转轮系曲柄连杆滑块机构

Fig.5 Combination of epicyclical gear train with crank-link-slider linkage

2.2.1 络交杆位移方程

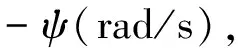
转化后轮系传动比为：

(9)

由式(9)可得二阶共轭从动非圆齿轮角速度为：

(10)

将式(10)对时间t进行积分运算，得到二阶共轭非圆齿轮角位移φ2为：

(11)

(12)

将矢量方程式(12)转化为解析方程式，可表示为：

(13)

式中：xO2=l1cosψ；yO2=l1sinψ；lDC为杆DB中DC段长度，mm。a3、a2、a1分别为：

xE=lDCcosα2+l4cosα3+xD

(14)

2.2.2 络交杆速度方程

位移方程组(13)等式两端对时间t求一阶导，可得速度方程组

(15)

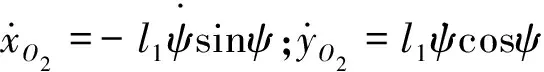
对方程组(15)求解并整理可得络交杆速度为：

(16)

式中

3 生丝卷装断面廓线计算模型的建立

若为等速络交得到的卷装断面形状理论上应为梯形(如图6中实线所示)，但实际中为减少冲击，络交杆往复换向时速度减小，造成换向点附近因速度小而使丝圈密度增加，因此实际中的卷装断面形状为马鞍形，如图6中点画线所示[3]。为分析卷装成形质量，学者们研究了影响卷装成形质量的工艺参数[17-18]，结果表明卷绕角是影响卷装质量的重要参数，卷绕角的大小取决于络交杆速度vE(mm/s)与小䈅周转速度v0(mm/s)的比值，即

(17)

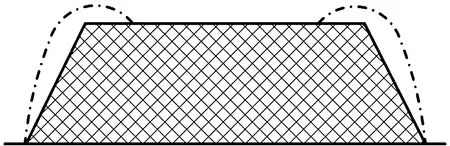
图6 卷装断面形状

Fig.6 Profile of winding section

在生丝卷装上取出一微元段，在这一微元段中单位轴向长度所卷绕的生丝量ξ与该段中丝线的条数N成正比，而与卷绕角λ成反比，其表达式为：

(18)

式中，k是与小䈅卷绕半径以及生丝比重等参数有关的常数。

由式(18)可得，在同等数量的生丝根数情况下，在计算出多次导丝之后卷绕角分布情况后，取其平均值αm(rad)，可用比值1/sinαm近似当前位置的生丝卷取量，连接这些数据点绘制成曲线，可求得近似的生丝卷绕成形断面廓线。

4 参数优化模型的建立及求解

为保证生丝卷装成形质量，本文以生丝卷装断面廓线理想几何特征为目标，以非圆齿轮传动特性为约束条件，利用遗传算法[19]对所设计卷绕机构进行优化设计，搜寻满足生丝卷绕工艺的非圆齿轮节曲线参数。

4.1 目标函数的建立

生丝卷装断面廓线如图7所示。其廓线理想几何特征包括：生丝卷装断面平整度高与生丝卷装平整段尽可能宽。设卷装廓线2峰点为hhigh1和hhigh2，mm；其与凹心处最低点hlow间的高度差值为Δh，即Δh=max(hhigh1,hhigh2)-hlow，mm；2峰点间宽度为Δw，mm；卷装总宽为W，mm；根据理想几何特征，建立参数优化目标函数：

1)丝线成形断面峰谷高度差与最高峰高度比值：d1=Δh/max(hhigh1,hhigh2)；

2)两峰间宽度与卷装断面总宽的比值：d2=Δw/W。

图7 生丝卷绕成形断面廓线

Fig.7 Ideal profile of silk forming

由生丝卷绕工艺可知，生丝卷装断面平整度更加影响卷装质量，即所建立的目标函数d1相对d2的权重更大，因此本文设定权重配比情况：d1∶d2=0.7∶0.3。则目标函数可表示为：

F=0.7d1-0.3d2

(19)

4.2 约束条件

为保证非圆齿轮副能够正常运转，应当保证非圆齿轮节曲线外凸，即非圆齿轮约束方程可表示为[20]：

(20)

4.3 优化参数

文中运用5种类型非圆齿轮设计了5种一阶和二阶共轭非圆齿轮驱动的卷绕机构，在进行参数优化时，优化参数为不同类型非圆齿轮节曲线参数，由2.1节非圆齿轮副节曲线方程可得不同类型齿轮优化参数为：

1) 一阶变性偏心圆齿轮及其二阶共轭非圆齿轮副，优化参数可表示为：

xq1=(xq11,xq12,xq13)=(r,e,m11)

(21)

2) 一阶变性椭圆齿轮及其二阶共轭非圆齿轮副，优化参数可表示为：

xq2=(xq21,xq22,xq23)=(A2,k2,m11)

(22)

3) 一阶变性巴斯噶蜗线齿轮及及其二阶共轭非圆齿轮副，优化参数可表示为：

xq3=(xq31,xq32,xq33)=(b,l,m11)

(23)

4) 一阶变性傅里叶级数齿轮及其二阶共轭非圆齿轮副，优化参数可表示为：

(24)

5) 一阶变性正弦齿轮及其二阶共轭非圆副，优化参数可表示为：

xq5=(xq51,xq52,xq53)=(ax,A1,m11)

(25)

4.4 优化结果与分析

当ψ=20 rad，l1=30 mm，l2=400 mm，l3=550 mm，l4=150 mm，lCD=400 mm，xD=-300，yD=43，H=100 mm，yE=30时，采用遗传算法以一阶变性巴斯噶蜗线齿轮及其二阶共轭非圆齿轮副驱动的卷绕机构为例进行优化运算，遗传算法基本参数为：种群中个体数目为20，遗传代数为100代，变量二进制位数为20，种群间个体选择比率为0.9，交叉概率为0.8，变异概率为0.2，参数优化过程如图8所示，当迭代到70代后，目标值F趋于稳定，由于所采用的遗传算法实质上为一类启发式随机搜索的算法，并且进行无缝编码，优化结果为全局最优解，其初始群体随机产生，存在一定的随机性，因此得到的结果并非绝对的最优解[21]。为保证非圆齿轮传动特性，选取非圆齿轮变形量最小的一组优化参数：

b=6.46 mm,l=39.13 mm,m11=1.01。

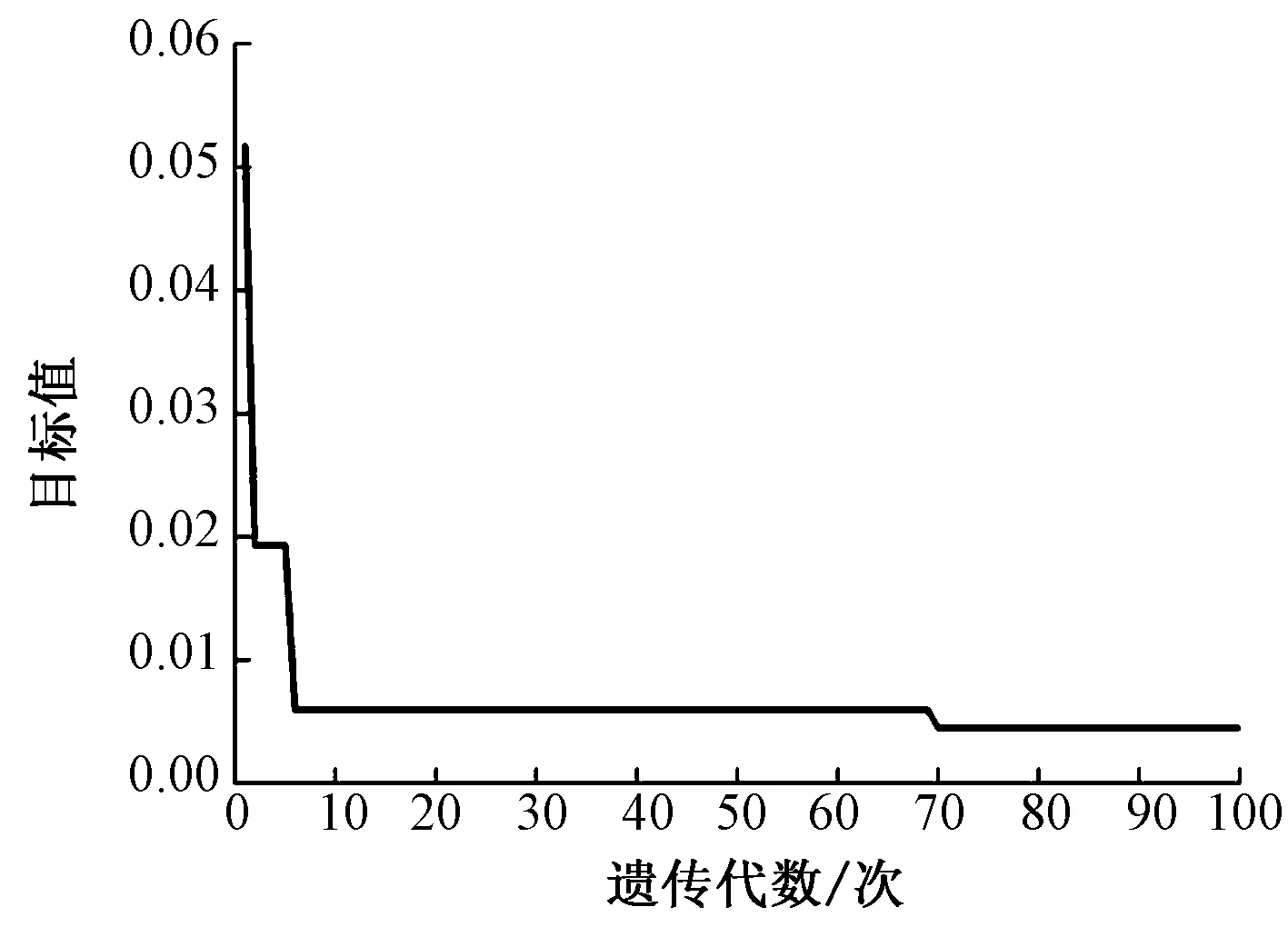
图8 遗传寻优结果

Fig.8 Genetic optimization results

该组参数对应的卷装断面廓线形状如图9所示：卷装断面廓线凹心现象并不明显，表面平整度较高；卷装成形总宽度约为65 mm，卷装平整段宽度为34 mm，平整段较宽。

图9 理论计算卷装断面廓线

Fig.9 Curve of silk section profile by theoretical calculation

5 试验验证

5.1 试验台研制

根据第1.2节非圆齿轮副驱动的卷绕机构工作原理和第4.4节优化后的机构参数。机架由截面尺寸为30 mm×30 mm的铝型材搭建而成，轴类件、蜗轮蜗杆传动及链传动采用机加工零件，非圆齿轮副及一些较为复杂的零件采用3D打印技术进行加工，鼓形结构的小䈅角半径为80 mm。为方便输入速度调整，动力源选用交流伺服电动机，型号为ASCM130-G10015LZ，额定电压为220 V，额定功率为1.5 kW，额定转矩 10 Nm，在试验过程中设定电动机转速为100 r/min。

5.2 生丝卷绕试验

5.2.1 试验步骤

1)进行空转试验，检查试验台各零部件的装配关系是否正确，各部件间的传动是否良好；

2)调整丝线位置，使丝线准确通过络交杆并卷绕在小䈅上；

3)启动丝线卷绕装置试验台，进行丝线卷绕试验；

4)观察得到的卷装，分析卷装断面廓线。

5.2.2 试验结果与对比分析

本文所设计的非圆齿轮副驱动的卷绕机构成形的卷装如图10所示。将非圆齿轮副换成1对偏心圆齿轮，即传统的周转轮系式卷绕机构，成形的卷装如图11所示。图10、11中用粗实线标识卷装断面廓线，细实线标注平整段宽度，通过量程为 150 mm 的直尺测量可得4.1节所述的断面廓线几何特征参数，如表1所示。

分析表1中数据可得：

1) 非圆齿轮副驱动的卷绕机构试验得到的丝线断面廓线与理论计算廓线几何特征参数基本吻合，验证了本文所建立的通用数学模型的正确性；

2) 非圆齿轮副驱动的卷绕机构试验所得的丝线成形断面峰谷高度差与最高峰高度比值为：

图10 非圆齿轮副驱动的卷绕机构成形的卷装

Fig.10 Package of winding mechanism driven by non-circular gear pairs

图11 周转轮系式卷绕机构成形的卷装

Fig.11 Package of winding mechanism driven by epicyclic gear train

表1 卷装断面廓线参数对比表

Tab.1 Comparison of silk section
profile parameters

mm

周转轮系式卷绕机构试验所得的丝线成形断面峰谷高度差与最高峰高度比值为：

表明非圆齿轮副驱动的卷绕机构卷装凹心现象并不明显，表面平整度相对较高。

3) 非圆齿轮副驱动的卷绕机构试验所得的卷装断面廓线两峰间宽度与卷装断面总宽的比值为：

周转轮系式卷绕机构试验所得的卷装断面廓线两峰间宽度与卷装断面总宽的比值为：

结果表明，非圆齿轮副驱动的卷绕机构卷装平整段相对较宽，验证了本文设计的卷绕装置在实际生丝卷绕作业中的可行性及其优越性。

6 结 论

1) 运用5种常用非圆齿轮，即偏心共轭非圆齿轮副、椭圆齿轮副、巴斯噶蜗线型非圆齿轮副、傅里叶级数型非圆齿轮副和正弦型非圆齿轮副，设计了5种混合阶数非圆齿轮副驱动的卷绕机构，并建立了其通用运动学数学模型。

2) 为保证生丝卷装成形质量，以生丝卷绕成形断面廓线理想几何特征为目标，以非圆齿轮传动特性为约束条件，利用遗传算法求解了通用参数优化数学模型，以混合阶数巴斯噶蜗线型非圆齿轮副驱动的卷绕机构为例进行优化运算，优选出了1组满足生丝卷装工艺的非圆齿轮节曲线参数：b=6.46；l=39.13；m11=1.01。

3) 根据参数优化结果，设计了生丝卷绕试验台，进行了生丝卷绕试验。非圆齿轮副驱动的卷绕机构试验得到的卷装断面廓线与理论计算廓线基本吻合，验证了通用数学模型的正确性；相对传统的周转轮系式卷绕机构，非圆齿轮副驱动的卷绕机构成形的卷装凹心现象不明显，表面平整度较高，且卷装平整段较宽，验证了本文设计的卷绕装置在实际生丝卷绕作业中的可行性及其优越性。

FZXB