基于并行约束延迟LMS的高速FPGA信息采集

赵永翼, 丁建楠

(沈阳师范大学 科信软件学院, 沈阳 110034)

0 引 言

在现实世界中,信号的应用已经占据了一个具有挑战性的地位。随着可编程逻辑器件的发展,现场可编程门阵列(FPGA)成为实现自适应滤波器的重要手段。FPGA在对相同的硬件进行重新编程方面表现出良好的灵活性,同时通过在较短的处理时间内启用并行计算实现了良好的性能。

自适应滤波器是根据优化算法自调整传递函数的滤波器。由于优化算法的复杂性,大多数自适应滤波器都是数字滤波器,它们执行数字信号处理,并根据输入信号来调整性能[1-3]。对于某些应用程序,需要自适应系数,因为所需处理操作的某些参数(例如某些噪声信号的特性)事先不知道。在这种情况下,通常采用自适应滤波器,它使用反馈来细化滤波器系数的值,从而得到它的频率响应。自适应滤波技术是近几十年来发展起来的信号处理理论的一个重要分支。它的主要特点是滤波器参数可以随着输入信号统计特性的变化而自适应调整,自适应调整可以使滤波器在最佳状态下运行,获得所需的输出信号。自适应滤波技术已广泛应用于通信系统、控制系统、雷达系统等领域。更重要的是,当这种技术应用于不同的应用程序时,它只是有不同的输入信号和期望的信号。调整过程涉及到成本函数的使用。例如,最小化输入的噪声分量,这是滤波器最优性能的一个准则,它决定了如何修改滤波器系数,以在下一次迭代中最小化成本。有维纳滤波器,它是平均平方误差的最优线性滤波器,以及几种试图近似它的算法,如最速下降法。还有一种最小均方算法,由Windrow和Hoff开发,最初用于人工神经网络[4-5]。算法的选择高度依赖于感兴趣的信号和操作环境,以及所需的收敛时间和可用的计算能力。利用IIR(无限脉冲响应)或FIR(有限脉冲响应)滤波器可以建立自适应数字滤波器。FIR本身是稳定的,因为它的结构只涉及正向路径,不存在反馈。反馈到输入端的存在可能导致滤波器不稳定,产生振荡。因此,滤波器的设计是通过FIR实现来实现的。

LMS的步长μ是一个非常重要的自适应过滤参数,同时它在参考信号功率、稳定控制、收敛速度和LMS的波动适应过程中也非常重要。当步长较大时,LMS算法收敛速度较快,但稳态均方误差(MSE)增大。另一方面,如果步长比较小,MSE的稳态较小,但收敛速度较慢。因此,步长在LMS算法的收敛速度和MSE的稳态之间提供了一个平衡。一个直观的方法来提高LMS算法的性能是使步长可变而非固定,也就是说,在LMS算法中选择大的初始收敛步长值,当系统接近其稳定状态值时,并使用小的步长值时,可以产生可变步长LMS算法。利用该方法可以获得较快的收敛速度和较小的稳态MSE。为了便于描述,首先在具有真实信号的系统辨识模型的背景下,建立了LMS算法。在信号传输过程中,由于介质性能的变化,会产生噪声和失真。这些变化可能是慢变化或快变化,大多数时间变化是未知的。自适应滤波器的应用使信号失真降至最低,在实时信号处理领域得到了广泛的应用。自适应滤波算法构成了滤波系数的调节机制,实际上与经典的优化技术密切相关。此外,自适应滤波器由于其实时自调整特性,在缓慢变化的环境中,可以有效跟踪一个最佳动作。自适应滤波器的输入输出关系取决于其传递函数。这种结构包括有限脉冲响应(FIR)和无限脉冲响应(IIR)滤波器。这对给定自适应算法的计算复杂度和自适应过程的总体速度有很大的影响。滤波器系数的自适应遵循特定目标函数或成本函数的最小化过程。

最小均方(LMS)算法作为自适应算法中的一种基本方法和重要方法, 具有计算量小、实现简单等优点, 具有良好的可用性。 然而, 传统的LMS实现难以满足实时需求和高速的数字信号处理。 而且,随着采样率、单处理单元容量和系统频率的提高, 严重增加了系统成本。 由于FPGA具有存储量大、粒度小、并行计算等优点, 在基于并行延迟LMS(PDLMS)的FPGA中建立了一种基于约束型的PDLMS自适应滤波结构。 随后, 将约束PDLMS应用于信息采集系统, 并将其性能与其他方法进行了比较。

1 自适应滤波算法

维纳滤波算法中,以均方误差表示的输出为最优,下面给出了最优输出系数的表达式:

w0=R-1p

(1)

其中:R为输入的相关矩阵;P为输入与期望响应之间的互相关向量。当信号统计量随时间变化时,即使用自适应滤波器的情况下,则必须重新计算输出系数。这需要计算两个矩阵,其中一个求倒数,然后把它们相乘。该算法不能实时计算,因此必须使用其他近似维纳滤波器的算法[6-9],可以使用最速下降法,收敛到最优滤波器权值或给定值。由于曲面(或超曲面)的梯度指向最大值的方向增加,则梯度的反方向(-)将指向曲面的最小点。通过使用一种方式来更新权值,可以自适应地达到最小值:

wn+1=wn+μ(-n)

(2)

其中,μ为步长参数,最小均方(LMS)算法类似于急降法,通过迭代逼近MSE最小值来调整权值。一开始这种方法用于训练神经网络。关键是,LMS算法不是每次都要计算梯度,而是使用梯度的粗略近似。误差en,在滤波器输出时可表示为

(3)

其中:dn是期望输出;un是滤波器的输入。利用误差可以求出半径的近似值:

=-2enun

(4)

将梯度的表达式代入急降法,权值更新得到

wn+1=wn+2μenun

(5)

其中μ为步长参数,定义了算法收敛到最优权值的速度。最速下降算法收敛或稳定的充要条件是μ满足:

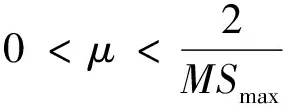
(6)

其中:M为滤波器数目;Smax为滤波器输入功率谱密度的最大值。因为它只涉及简单的加法和乘法,因此,这是首选的方法。

2 改进的LMS算法

当LMS算法在硬件上实现时,这种硬件实现带来了计算瓶颈,限制了迭代速度。为了解决这个问题,Herzberg提出了一种延迟LMS算法[10-14]。然而,延迟LMS算法中存在的时延信息对算法的收敛性能有很坏的影响,当滤波器阶数变大时,算法的收敛性能更差。针对这些不足,提出了一些算法,以提高算法的收敛性能为代价,增加了运算复杂度。

并行延迟LMS算法是一种将延迟和并行技术相结合的LMS算法。在相同条件下,PDLMS算法比延迟LMS算法的步长限制小,收敛速度快,数据吞吐量高,同时保持了延迟LMS算法高效、简单的优点。

LMS算法表达式如下:

其中,w(n)=[w0(n),…,wN-1]T是自适应滤波系数,x(n)=[x(n),…,x(n-N+1)]T是输入信号序列,y(n)是输出信号,e(n)预测错误信号,d(n)是期望信号序列,μ是步长参数和N是自适应滤波长度。

需要注意的是,LMS算法的误差e(n)是在执行了一次乘法和n次顺序加法之后产生的。N个顺序的加法限制了LMS算法的吞吐率[15]。为了获得更高的吞吐率,引入了LMS算法和DLMS算法,其表达式可以写成

其中D为插入LMS算法误差反馈路径的总延时。如果D=0,则式(4)表示常用的LMS自适应算法。

一个N-tap FIR滤波器可以在时域表示为:

(13)

输入序列可分解为偶数部分x0(n)和奇数部分x1(n),如下:

同样,长度为n的滤波系数w(n)也可分解为偶数部分w0和奇数部分w1。偶数输出序列和奇数输出序列可以计算为:

当并行技术应用于延迟LMS算法时,得到PDLMS算法。以2个并行PDLMS算法为例,每个输出分支需要2个输入分支进行自适应处理。并行PDLMS算法可分为6个部分:

为了更好的收敛性和稳定性,可以在PDLMS算法中引入约束。对于变步长或噪声均可施加约束,以获得较快的收敛速度和较小的稳态MSE。约束PDLMS算法与PDLMS具有相同的形式,但在适应的过程中该算法步长μ是改变的。通过改变算法步长,可以改变算法的收敛速度,以及权系数在最优值附近的变化量。

步长在每次迭代中更新,更新后的步长为:

(22)

因此,约束最小均方算法实现步骤如下:

1) 初始化权重向量为0;

2) 初始化μ值;

3) 通过e(k)=d(k)-y(k)计算错误信号;

4) 更新权重函数:w(k+1)=w(k)+2μ(k)e(k)x(k);

5) 通过公式(22)更新步长。

3 改进的LMS算法在FPGA中的应用

通常FPGA实施过程中,会注重以下几个方面:1)定义需求和规范;2)为设计概念建立符合规格的系统模型;3)用VHDL语言实现系统模型;4)模拟VHDL来确定它是否符合系统规范;5)使用VHDL描述综合设计;6)通过仿真验证,综合设计仍然满足要求;7)将综合设计方案编制成硬件;8)对实际设备和电路进行测试,并与原要求进行性能比较。

本文利用Altera公司的旋流器装置和QuartuslI软件实现了约束PDLMS算法的硬件实现。设置阵列天线个数为4,延迟信息为6个时钟档位,滤波参数为8。

为了便于PDLMS算法的实现,将系统划分为多个模块,从而达到直观、易于校正的优点。根据PDLMS算法的特点,可以将系统分为4个模块,如图1所示,PMx是相应的处理模块。利用FIFO的存储结构,可以将AD的样本数据分解为偶数部分和奇数部分。PM1是误差产生模块,接收PM3的权值w0和PM2的输出yP2,将误差信号e0和输出数据yP1放入PM3和PM2中。图2所示的PM1包括延迟单元、加法器单元、减法器单元和乘法器单元。

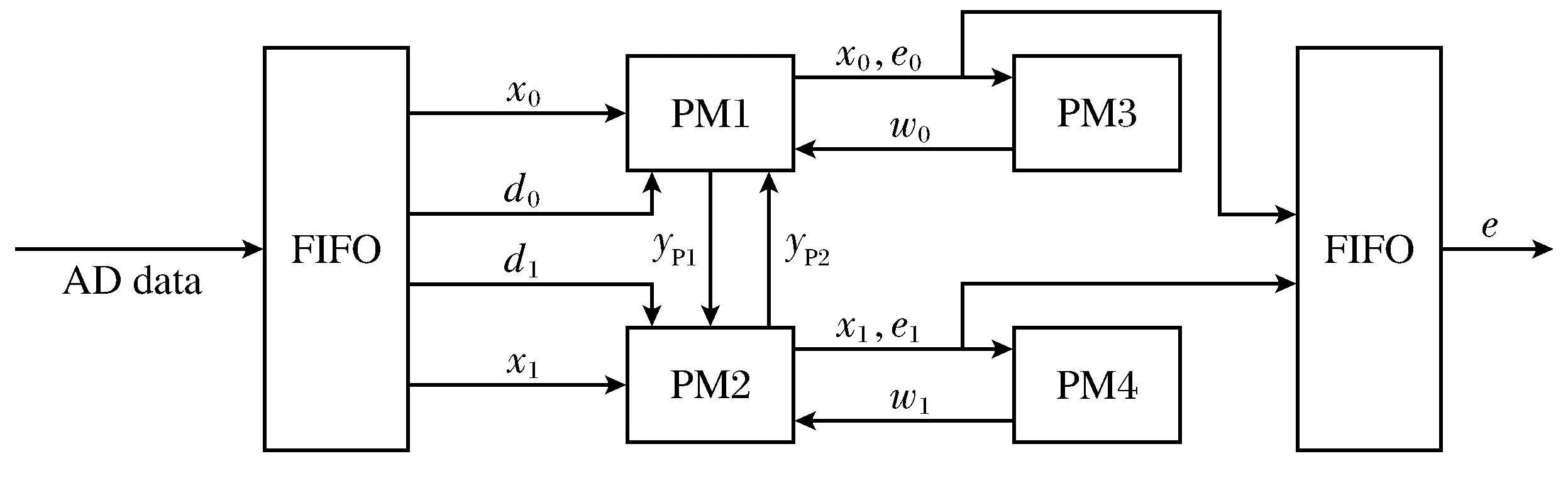
图1 约束PDLMS的实施方案Fig.1 Scheme of Constrained PDLMS

图2 PM1结构Fig.2 Structure of PM1

PM3是更新权值的单位,其I/O参数为x0,e0,w0。PM3的模块包含与PM1相同的单位。PM2和PM1内部单位相同,但输入参数不同。同样,PM4和PM3也具有相同的处理单元。可以利用模块复用的结构高效的来实现该算法。此外,PM3和PM4的迭代模块可以在同一时间的不同计算节点上运行。该计算特性可大大提高系统的并行性,提高系统的运行率,保持系统的实时性。

图1、图2直观地表示了约束PDLMS算法的流程结构。为了实现该算法,可以用IP核代替处理单元。为了降低资源消耗,提高运行速度,采用数据转移的方法实现步长因子的更新。

4 实验分析

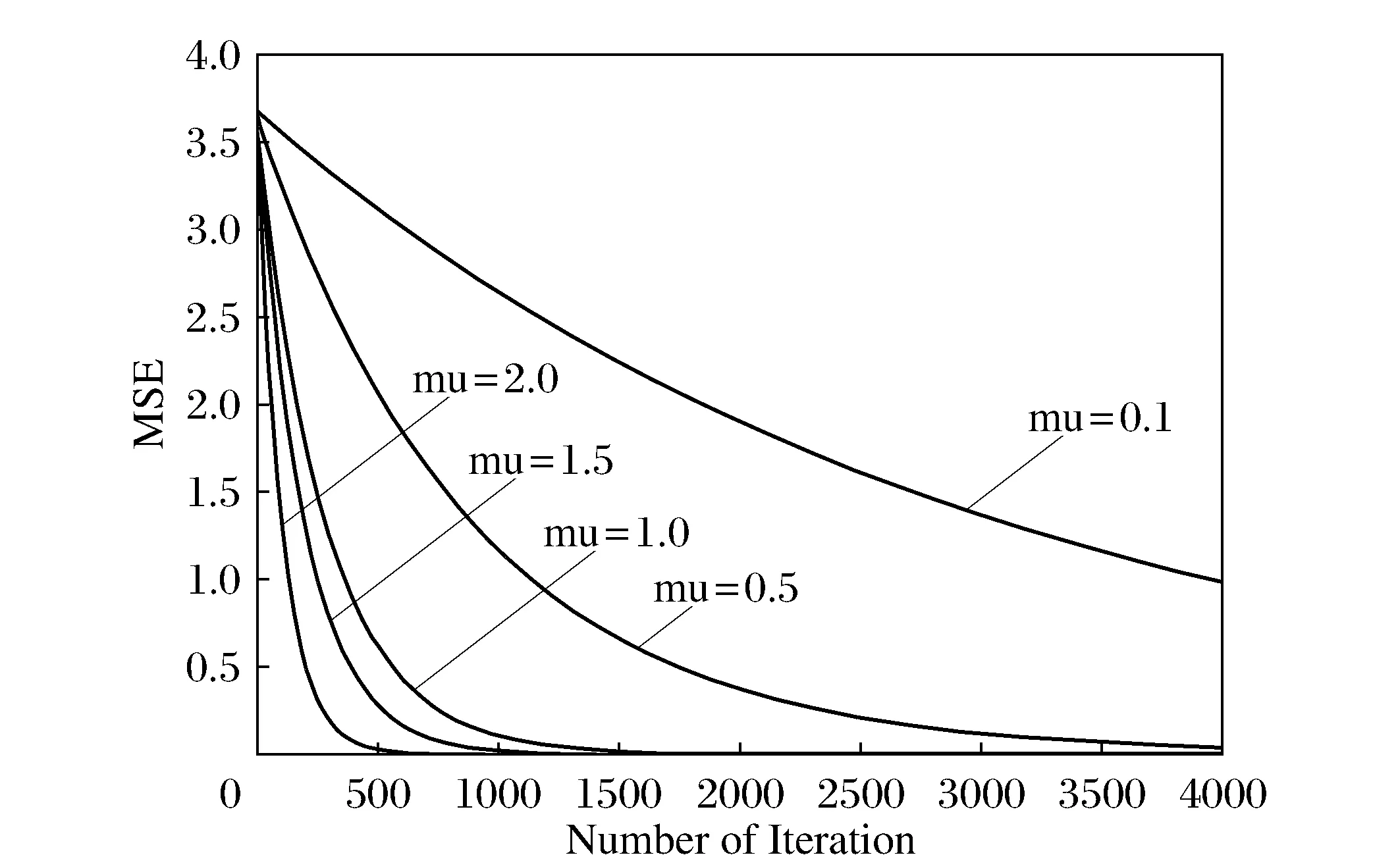
图3 步长因子对MSE的影响Fig.3 The effect of step size on MSE

为了说明本文提出方法的有效性,与文献[16]及以DLMS作比较。文献[16]仅提出一种并行延迟LMS算法,而本文对这种方法进行了一种有效的约束,使得信息采集及抑制噪声效果非常好。以导航干扰系统为应用背景,在室外环境模拟条件下进行了强干扰信号的处理。干扰的中心频率为1 575.42 MHz,带宽为10 MHz。干扰信号比为60 dB,采样速率为65.28 MHz。首先分析了LMS中不同步长因子对MSE值的影响,如图3所示。

根据图3分析,采用相同的步长因子μ=2,实现约束PDLMS和DLMS算法与文献[16]的对比。

通过对实测数据的处理,3种算法的收敛性能如表1所示。

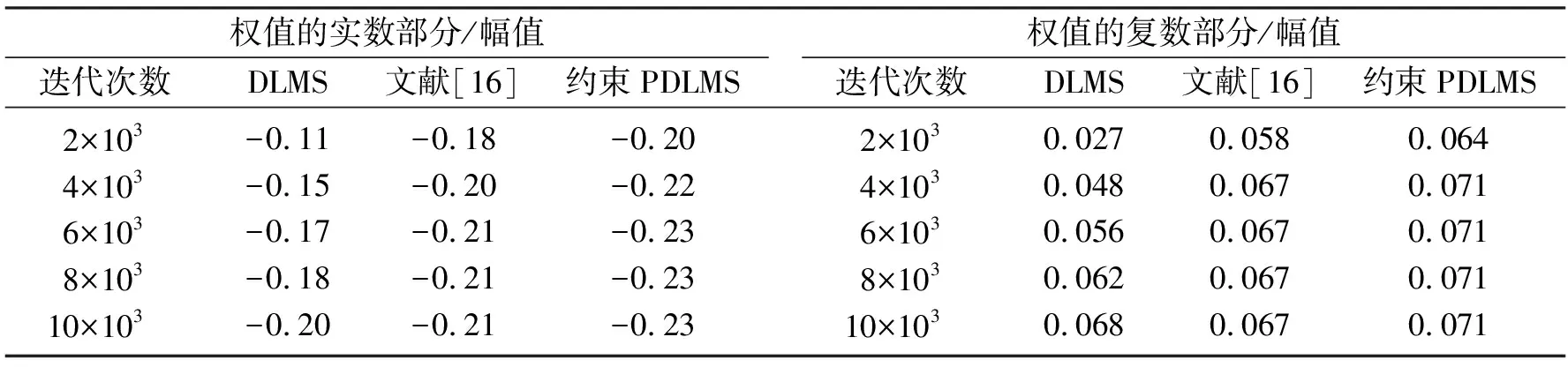
表1 3种算法的收敛比较Table 1 Convergence comparison of the three algorithms

约束PDLMS算法具有良好的收敛性能。一方面,约束PDLMS算法的滤波长度是DLMS算法滤波的一半。另一方面,算法权值的更新率是采样率的一半。整体上比文献[16]收敛性有一定的提高。

表2 数据吞吐量比较Table 2 Comparison of data throughput MHz

系统的采样时钟为60 MHz。对于2个并行约束PDLMS算法,输入数据的采样时钟为60 MHz。将输入数据分为偶数和奇数部分后,样本时钟变为30 MHz。因此当约束PDLMS算法处理输入数据时,算法处理时钟为30 MHz。然而,对于传统的DLMS算法,输入数据的采样时钟和算法处理都是60 MHz。在同一采样时钟中,n个并行约束PDLMS算法的处理时钟是DLMS算法的第n个处理时钟。文献[16]中所采用的也是2个PDLMS算法,因此它与2个并行约束PDLMS的吞吐率是一样的,在实际应用中,DLMS算法不能满足实时处理输入数据的要求。约束PDLMS算法采用并行输入输出结构,减少了计算时钟,实现了对高速率数据的自适应运算。表2显示了3种相同的算法处理时钟之间的差异。

5 结 论

随着LMS算法的发展,硬件需求随着时钟运行速度的提高而急剧下降,这给FPGA的信息快速获取提供了一个挑战,但是伴随着很多问题的出现。因此,本文提出抑制约束PDLMS方法来实施FPGA的信息获取,更新其动态约束步长,结果表明,本文提出的约束PDLMS方法是可行的。其性能优于传统的最小均方算法和全矩阵实时自适应数字信号处理算法,对比结果也表明,提出的新方法具有功耗低、吞吐量高等优点。