基于最小二乘法的五轴机床静态误差建模

赫焕丽,王 量

(1.咸宁职业技术学院 工学院,湖北 咸宁 437100; 2.河南科技大学 机电工程学院,河南 洛阳 471003)

数控机床的加工精度是衡量一个国家制造业发展水平的重要标志,在社会的发展中得到了广泛应用.静态误差是影响数控机床精度的重要因素,静态误差主要包括装配误差、弯曲误差及热误差等[1].与动态误差相比,静态误差在机床操作过程中变化缓慢.若不能对机床静态误差进行有效补偿,长时间操作机床,就会造成零件加工精度降低.因此,研究机床静态误差预测模型,及时进行误差补偿,对于提高机床精度具有重要意义.

误差补偿法不需要对机床设计结构和制造进行变更,成本较低,已成为提高机床精度的良法[2].为了预测机床加工零件产生的误差,许多学者对机床误差模型进行了研究.文献[3-4]采用径向基网络模型预测机床主轴热误差,建立机床主轴测温点分布图,引用径向基函数建立热误差与温度变化的神经网络模型,通过实验验证热误差模型的合理性,从而降低了机床主轴产生的热误差.文献[5-6]采用多元线性回归法预测机床静态误差,分析机床结构特点和误差来源,确定机床温度测量点,采用概率统计方法对机床误差数据进行分析,通过多项式曲面拟合理论创建静态误差预测模型,获得较好的预测精度.文献[7-8]采用多体动力学理论预测机床静态误差,通过ANSYS软件分析机床最大变形位置,对机床各个轴运动分别建立误差转换矩阵,根据多体动力学理论创建静态误差预测模型,采用实际测量验证预测模型,从而判断预测模型的可行性和准确性.但是,以往研究机床静态误差预测精度较低,不能很好地对静态误差进行在线补偿.对此,本文以五轴机床为例,采用矩阵变换分析机床五轴静态误差,通过最小二乘法建立机床静态误差预测模型,采用激光跟踪器测量机床实际产生的误差,并与预测模型进行比较,为深入研究机床静态误差建模方法提供参考价值.

1 机床静态误差模型

本文采用的五轴机床移动轴为x,y,z,旋转轴为y和z.机床静态误差可以通过一系列齐次变换来表示,这个系列由交替关节和形状变换组成.主轴位置误差变换方程式[9]为

(1)

式中:φB,φw分别为y轴旋转角度和z轴旋转角度;φx,φy,φz为移动距离;Ti为误差矩阵.

为了将旋转、平移误差引入到坐标系和关节转换中,在坐标系转换中引入常数(不依赖位置)的误差分量,而位置相关的分量被引入到关节变换中.对于机床来说,有3种类型的转换.

1.1 坐标系转换

对于机床3个直线轴而言,静态误差为3个垂直度误差,如图1所示.图1中:x,y为理想坐标轴;x1,y1为测量数据拟合的坐标轴.

实际坐标系转换后的误差矩阵表达式为

(2)

式中:αi,βi和γi为z,y和x方向旋转误差;[xiyizi]T，[ΔxiΔyiΔzi]T分别为坐标系位置和位置误差.

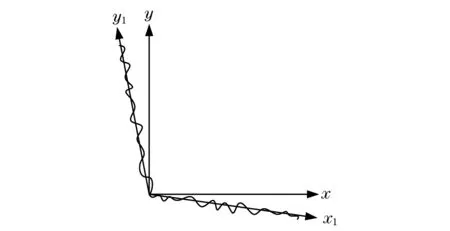
图1 静态误差测量方法Fig.1 Static error measurement method

1.2 旋转转换

理想的旋转接头(旋转轴y轴)的联合变换可以表示为

(3)

式中:B为关节的旋转角位移.

关节在转动过程中,可能会引起几个误差动作.当节点控制位置B时,可能产生定位误差β.此外,旋转误差可能引入倾斜角α和γ,由于转动误差dx,dy和dz的积累,整个桌面发生移动.假设旋转角度很小,实际旋转关节(绕y轴旋转)的变换误差为

(4)

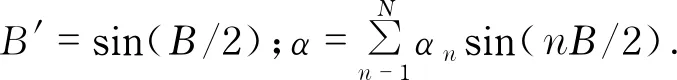
1.3 移动关节转换

移动关节在实际运动过程中,会产生误差,包括沿着关节的位置误差、直线误差和角度误差.对于变换矩阵来说,误差项是关节位移的函数,即

(5)

式中:x为被控制的关节位置;δx为定位误差;dα/dx,dβ/dx和dγ/dx为角误差的累积率.

1.4 体积误差模型

主轴框架中刀具的实际坐标变换表示为

(6)

采用一阶正运动学方程消除误差的二阶项和高阶项,其方程式为

(7)

H为式(1)中得到的理想正运动学,由理想的机床关节和支撑它们的结构元件尺寸决定ΔH为一阶项误差.

因此,机床的体积误差分量可以定义为实际和理想正运动学的差值，即

(8)

式中:e为误差向量;T0为形状变换参考矩阵;rt为机床主轴位置.

2 误差模型参数识别

误差模型中的参数估计是通过观察其工作空间中不同位置的机床体积误差来完成的,如图3所示.然而,要做到这一点,激光跟踪器进行测量的框架必须首先在误差模型的参数得到之前进行估计.这是在以下两个步骤中完成的.测量框架与表架(从机床的运动学模型)之间的关系是由齐次变换矩阵T0获得的.

2.1 测试框架

为了识别T0,假设在式(1)中定义的机床理想运动学方程式为

(9)

T0的方程式[10]为

(10)

式中:rt0为测量框架中的图像.

对于不同的关节命令(或测量点),机床的运动学传输H会有所不同.对于第i个测量点,在正向运动学传输和激光跟踪器记录的测量之间的误差矢量ei方程式为

(11)

式中:qi为跟踪器测量值.

2.2 误差模型

模型在参数集合中是线性的,可以用一个误差参数向量来表示,即

(12)

式中:M,P为矩阵.

考虑一个观察集由在n点观察到的误差组成,假设每个点都能观察到误差的情况下,采用的误差模型[11]为

(13)

式中:ei=[ex,iey,iez,i]T为误差矩阵;Mi为观察到相应的3×32关系矩阵；N为高斯分布的概率密度函数，N(0,δ)，δ为标准差.

因此,可以建立一个3n方程组来估计误差参数

(14)

式中:e=[ex,1ey,1ez,1…ex,ney,nez,n]T∈R3n为点集里测量误差向量的分量;M=[M1T…MnT]T为新矩阵系数.

采用最小二乘法[12-13]估计p′,式(14)变换为

(15)

3 结果与讨论

为了识别误差预测模型,对机床主轴上的刀具进行测量,在测试中采用激光跟踪器,如图2所示.

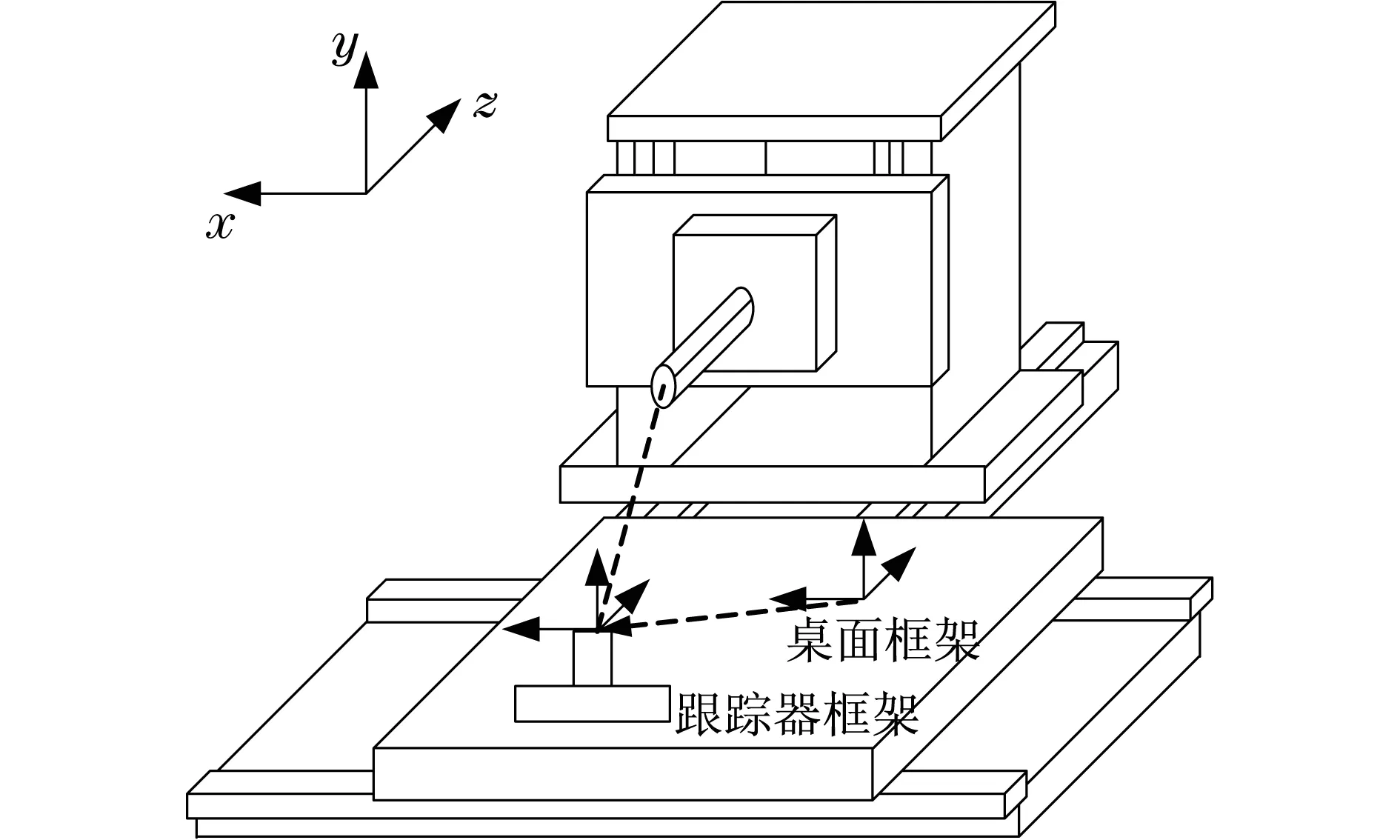
图2 刀具静态误差测量示意图Fig.2 Schematic diagram of static tool error

假设机床主轴转速为2 000 r/min,每5 min记录一次测量数据,记录32组数据.每次测量误差计算为

ei,j=

(16)

式中:ei,j为第i点的第j项误差;[xi,jyi,jzi,j]为第i点的第j次测量;[xiv,yiv,ziv]为第i点的平均测量值.

机床主轴分别安装50和100 mm长度刀具,采用最小二乘法和线性回归法预测机床静态误差结果,分别如图3和图4所示.

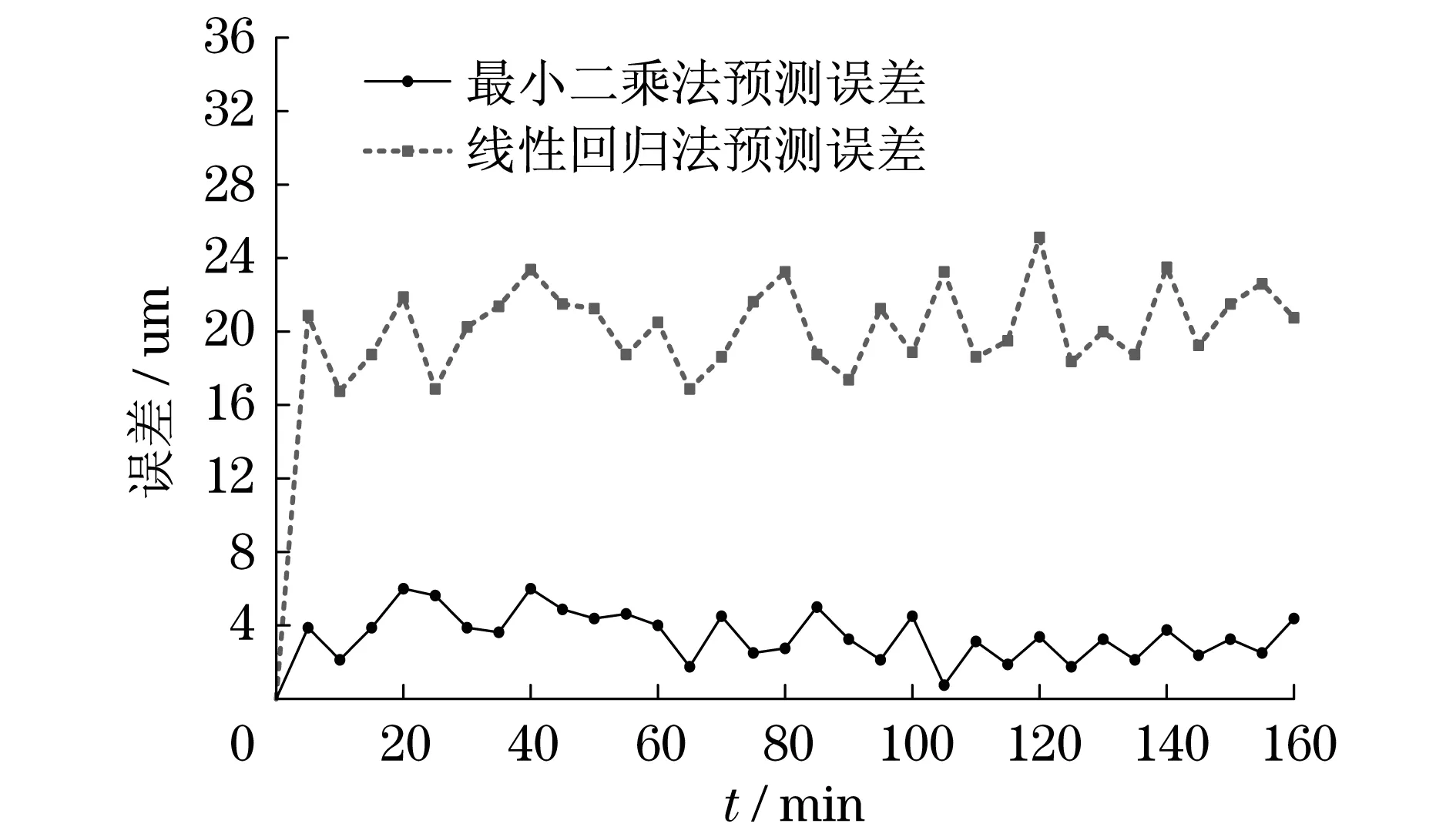
图3 短刀具测量误差(50 mm)Fig.3 Short tool measurement error(50 mm)

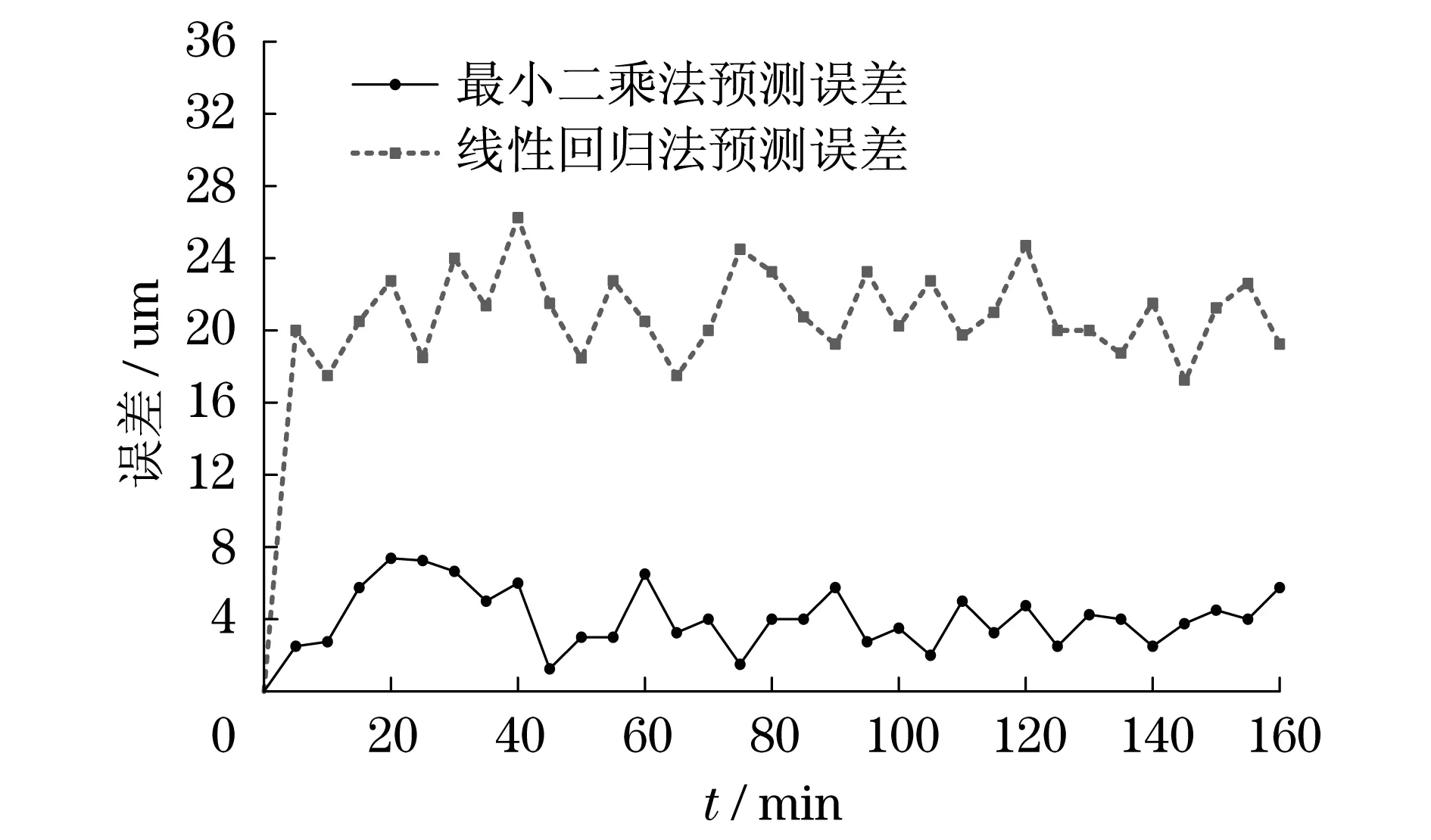
图4 长刀具测量误差(100 mm)Fig.4 Long tool measurement error(100 mm)

由图3可知:机床主轴静态误差采用线性回归法预测模型,产生的误差最大值为25.33μm,均方根值20.67μm,误差变化幅度较大;而采用最小二乘法预测模型,产生的误差最大值为5.94μm,均方根值为3.75μm,误差变化幅度较小.

由图4可知:机床主轴静态误差采用线性回归法预测模型,产生的误差最大值为26.67μm,均方根值21.32,误差变化幅度较大;而采用最小二乘法预测模型,产生的误差最大值为7.44μm,均方根值为4.52μm,误差变化幅度较小.因此,随着刀具长度的增加,预测结果偏差也会增加.同时,采用最小二乘法预测结果与实验测量结果符合度较高,能够提高机床主轴加工精度.

4 结论

针对机床主轴静态误差问题,采用了最小二乘法建立误差预测模型,并与线性回归法预测结果进行比较,主要结论如下:

(1) 机床主轴在旋转过程中,由于装配存在误差及运行产生热变形,导致机床主轴产生静态误差现象.

(2) 机床主轴长度不同,加工过程中产生的误差也不一样,长度越长,产生的静态误差也越大.

(3) 采用最小二乘法对机床主轴静态误差进行预测,预测精度较高,为机床主轴加工误差补偿提供理论依据.