空天飞行器姿态直接力/气动力复合控制

李爱军, 王瑜, 郭永, 王长青

(西北工业大学 自动化学院, 陕西 西安 710129)

空天飞行器(aerospace vehicle,ASV)是一种多用途高超声速航空航天飞行器。其完整飞行过程包括上升段、入轨段、在轨段、巡航段、再入段、末端能量管理段和自动着陆段。ASV再入过程中,飞行环境恶劣且变化剧烈,马赫数变化范围为25～6。因再入段初期动压过低,气动舵面操纵效率不足,仅靠气动舵面难以满足飞行器姿态控制需要,因此通常启动反推力控制系统(reaction control system,RCS)协助气动舵面共同完成姿态控制任务。RCS采用质量排出型推力器,利用喷流的反作用力产生控制力矩。RCS的工作原理决定了其力矩输出具有离散性和非线性的特性。如何实现RCS和气动舵面2种异构执行机构协同工作是空天飞行器控制系统设计需要解决的关键问题。

对于采用复合控制策略的飞行器,由于执行器结构差异性较大,多采用控制器与控制分配独立设计的思想,即保留控制器结构,通过控制分配[1-2]的方法进行处理。在控制器设计方面,为了在再入段剧烈环境变化的情况下提高ASV控制系统的跟踪性能,文献[3]在采用干扰观测器的基础上设计了自适应滑模控制器,有效地提高了控制器的控制精度和收敛速度;文献[4]基于滑模干扰观测器设计了控制器,实现空天飞行器的姿态跟踪控制。文献[5]将自适应与反步控制结合,实现对不确定项边界的估计,引入鲁棒项抑制扰动,实现了飞行器的姿态跟踪。神经网络技术具有对任非线性连续函数的逼近能力,能够对外界扰动,不确定情况进行有效估计,且采用权值自适应律可以实时调整控制器参数从而保证网络的逼近性能,因此在飞行控制系统设计中得到了广泛应用[6]。文献[7]采用神经网络干扰观测器对动态逆误差进行在线逼近并补偿。文献[8]基于神经网络观测器对气动建模误差进行补偿,以F-16战机气动模型为例验证了姿态控制的有效性。

尽管上述方法在一定程度上取得了良好的收敛速率与控制精度,但跟踪误差收敛时间不能精确估计,仅能保证系统渐近稳定,不利于处理ASV的快时变特性。而有限时间控制能使系统在有限时间收敛,具有良好的快速性与抗扰动能力,在处理快时变特性上有明显优势[9]。文献[10]针对具有系统外部扰动和参数不确定性的再入段空天飞行器设计了有限时间自适应终端滑模控制器以解决再入段姿态控制问题。文献[11]在有限时间积分干扰观测器基础上设计了有限时间控制器以实现再入段姿态指令的有限时间跟踪。

在控制分配方面,文献[12]首先把RCS当做连续力矩输出,然后再根据脉宽调制算法把连续控制量调制成离散的RCS开关控制量。文献[13-14]基于线性规划理论研究了控制力矩实时分配方法;文献[15]采用基于T-S模糊多模型控制方法,结合控制分配策略,将控制力矩分配到气动舵面与RCS执行机构,在设计过程中将RCS当作连续执行机构,忽略了其开关特性。文献[16]提出一种动态逆解算的RLV混合规划控制分配方法,实现了各操纵机构的优化使用。

本文针对空天飞行器再入段初期的姿态控制问题,基于RBF神经网络,自适应控制、滑模控制理论和控制分配技术提出了一种有限时间复合控制策略。与上述文献相比本文的创新之处在于:①利用滑模控制理论和控制分配技术提出了一种有限时间复合控制策略。②针对RBF神经网络易受逼近误差影响的问题,本文利用自适应控制补偿神经网络的估计误差,该方法使得设计控制器时不需已知逼近误差界值,方便了控制器的设计与参数选取。③该控制策略在保证ASV姿态跟踪误差有限时间收敛的同时,实现了对直接力与气动力的协调使用。

本文结构如下:第一部分建立了存在外部扰动和参数不确定性的ASV再入段姿态模型。针对此模型,第二部分提出一种RBF神经网络有限时间滑模控制器,得到使姿态角误差有限时间收敛的虚拟控制力矩,基于Lyapunov理论分析了系统的稳定性。第三部分运用控制分配技术,将虚拟力矩映射到气动舵面和RCS装置,提出直接力/气动力复合控制策略。第四部分给出所提出复合控制策略下系统的仿真结果并分析。第五部分给出本文的结论。

1 模型的建立

本文采用空天飞行器再入段简化姿态方程,具体描述如下[17]

(1)

式中,I∈R3×3是对称正定的转动惯量矩阵,ω∈[p,q,r]T是角速率向量(滚转,俯仰和偏航角速率),Ω=[μ,β,α]T是角度向量(倾斜,侧滑和迎角),u∈R3×1是控制力矩向量,d∈R3×1是不确定外部扰动,反对称矩阵ω×如下所示

(2)

姿态转换矩阵R(·)如下所示

(3)

由于ASV再入段飞行过程中几乎不产生侧滑,可视为β=0,故R(·)可简化为

转动惯量I=I0+ΔI,其中ΔI为系统不确定性,I0如下所示

(4)

控制信号u实际由气动舵面(包含升降舵,副翼和方向舵)和RCS喷头共同作用产生,公式如下所示:

(5)

式中,Daero∈R3×n,DRCS∈R3×m分别为气动舵面和RCS系统基于气动数据的安装矩阵;δaero∈Rn,δRCS∈Rm分别为气动舵面偏转向量和RCS喷头开关状态向量。

受文献[18]启发,转换姿态方程如下

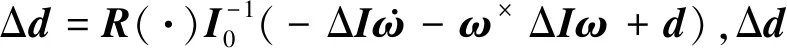
定义姿态跟踪误差e=[eΩ,eω]T

eΩ=Ω-Ωd

(8)

(9)

利用所定义的跟踪误差,对系统方程进行重新整理可得

(10)

2 神经网络有限时间滑模控制器

引理1[19]针对系统

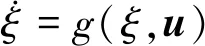
(11)

假设存在连续可微函数V,使其满足下列条件:

1)V为正定函数。

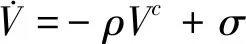
引理2[20]根据RBF神经网络的局部特性,径向基函数网络在有足够多的节点,且有适当构建的节点中心及中心宽度的情况下,能够对任意连续函数Q(X)在有界闭集ΩX内任意逼近,存在如下表达式

Q(X)=W*Th(X)+η(X)

(12)

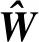
假设1RBF神经网络理想逼近误差η(X)有界,且界值为未知正常向量η0,|η|≤η0。

假设2广义扰动Δd有界。

定义sigλ(ζ)=[|ζ1|λsgn(ζ1),…,|ζn|λsgn(ζn)]T,0<λ<1。‖·‖F为矩阵F-范数。‖·‖为矩阵2-范数。

设计滑模面如下

(13)

f(eΩ)=[f(eΩ1),f(eΩ2),f(eΩ3)]T

(14)

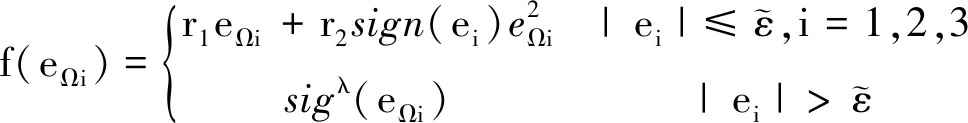
(15)

(16)

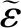
在(13)～(16)式所示滑模面的基础上,设计滑模控制律,神经网络自适应律,补偿自适应律如下

(17)

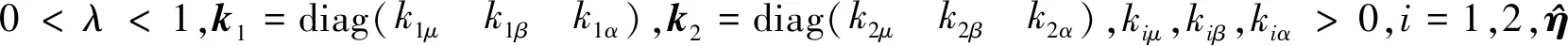
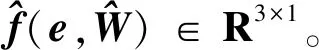
定理1对于(10)式所示的误差二阶系统,当采用滑模面(13)～(16)式及控制律(17)～(19)式时,以下结论成立:

1) 滑模面s实际有限时间收敛;

2) 姿态角跟踪误差eΩ实际有限时间收敛;

3) 姿态跟踪误差变化率eω实际有限时间收敛。

证首先,构造如下Lyapunov函数

(21)

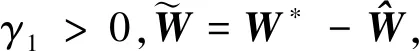
对V求导可得

(22)

将控制律(17)式代入上式得

(23)

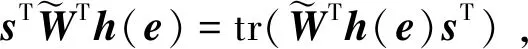
(24)

代入(18)式、(19)式并整理可得

(25)

构造Lyapunov函数

(26)

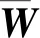
对V1求导可得

(27)

结合(10)式,控制律(17)式与(27)式得

(28)

进一步整理可得

(29)

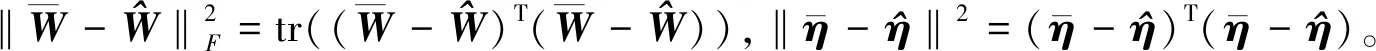
(30)

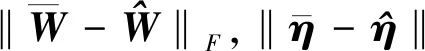
从而有

(31)

式中，eΩi=[eΩ1,eΩ2,eΩ3]。

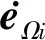
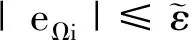
(32)

则

(33)

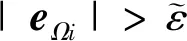
(34)

选择Lyapunov函数

(35)

对V2求导可得

(36)

根据引理1和(36)式可以得出,V2是实际有限时间收敛的。进而得出eΩi是实际有限时间收敛的。进一步得到

(37)

至此,定理1得证。

3 直接力/气动力复合控制分配

RCS是一种以推进器为执行机构的微型火箭发动机系统,其主要作用是为飞行器提供再入姿态控制、入轨变轨、空间交汇等方面提供微小力矩的修正。由于临近空间的空气密度随着高度的增加而变薄,仅使用气动舵面无法达到所需扭矩。因此,使用RCS和气动舵面组合的方案可以满足控制性能。

本节设计了一种控制分配算法,将RCS和气动舵面结合起来产生控制力矩Mc,该力矩由上一部分设计的有限时间滑模控制器获得,采用动压分配法设计2种执行机构的力矩分配权重,即

(38)

式中,μaero表示气动力占控制力矩的比重,其大小由实时动压决定;q为实时动压;q1,q2为复合控制分配与仅机动多面分配的切换点动压值。若气动力矩能完全提供所需控制力矩,则μaero=1。

对于气动舵面控制分配,首先要设计代价函数,因此要考虑2个方面:第一,要保证气动舵面产生的控制力矩与控制器输出的期望力矩误差尽可能小;第二,在满足舵偏速率与幅度的情况下,要保证气动舵面的偏转尽可能小。因此代价函数设计如下

(39)

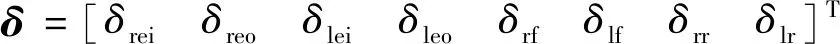
并且舵偏δ需要满足一定的位置与速率约束

δmin≤δ≤δmax

(40)

因此,气动舵面的控制分配问题就转化为了非线性规划问题。

对于RCS系统的控制分配,针对其喷头只有开、关2种状态,设计了一种混合线性整数规划算法。

首先定义一个松弛变量

usMRCS-DRCSδRCS

(41)

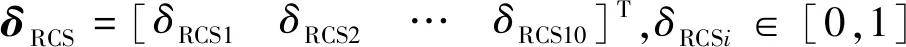
定义如下代价函数

(42)

满足

(43)

并且

(44)

式中,wroll,wpitch,wyaw为与us对应的三通道误差权重,wRCS=[w1,w2,…,w10]T,如此设计的主要目标是最小化量化误差,不使喷头产生的每个轴上实际力矩高于连续控制力矩。次要目标是在任意给定时间内同时开启的喷头数量达到最小以节省推进器燃料。要求

wroll,wpitch,wyaw≫w1,…,w10

wi=0.01,i=1,…,10

(45)

wroll,wpitch,wyaw取值如下

(46)

(44)式这一约束保证了喷头产生的有效力矩大小不能超过控制律产生的力矩大小。

至此,直接力/气动力复合控制分配策略确立。

4 仿真结果及分析

本节将通过数字仿真验证所提出复合控制策略的正确性。姿态控制及控制分配系统结构如图1所示。

图1 空天飞行器姿态控制系统结构

本文仿真选取再入飞行初期某阶段。初始条件如下：

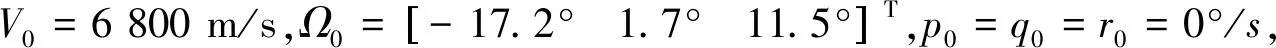
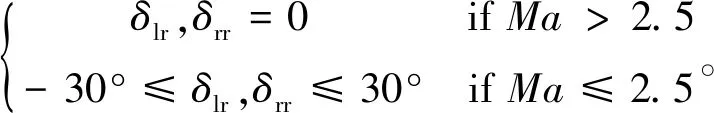
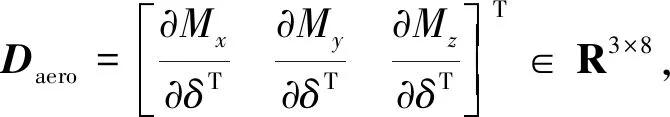
RCS安装矩阵DRCS由文献[21]给出,如下所示

DRCS=

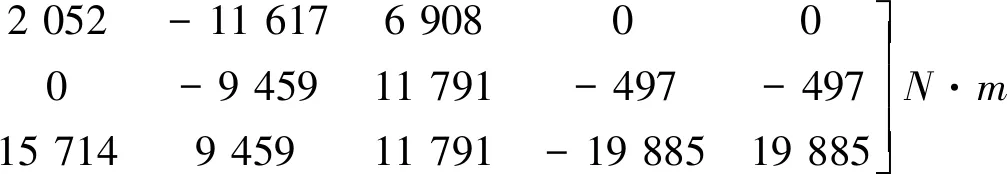
仿真结果如图2～10所示。图2和图3分别为ASV跟踪目标姿态角时姿态角误差和姿态角速率误差。从图2～3可见,所设计的有限时间滑模控制器完成了ASV的姿态跟踪,且跟踪误差在5 s左右收敛至0附近。图4为神经网络对外部扰动的估计值,从图中可以看出,神经网络能够快速对扰动进行估计,在4 s左右估计值跟踪上扰动值,估计效果较好。

图2 姿态角跟踪误差

图3 姿态角速率跟踪误差

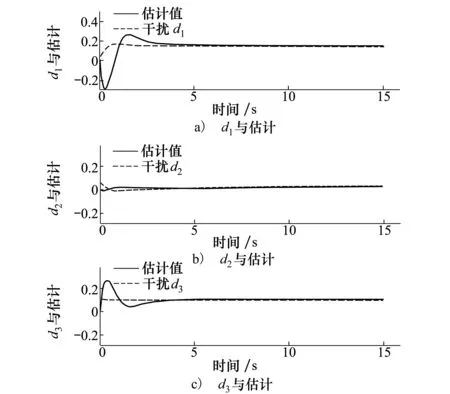
图4 RBF神经网络对广义扰动的估计

图5～9是ASV跟踪目标姿态角时的舵面偏转和RCS喷头开关状态。可以看到,在姿态跟踪过程初期舵偏较大,升降副翼和襟翼都达到偏转饱和状态。因此RCS系统作用产生额外的控制力矩以弥补总控制力矩的不足。4 s左右时,当气动舵面能提供足够的控制力矩时,RCS系统停止作用,喷头关闭。图10是直接力/气动力复合控制策略下姿态角跟踪曲线与无RCS作用,仅在气动力作用下姿态角跟踪曲线对比,可以明显看出,仅靠气动舵面偏转不仅不能实现姿态角的准确跟踪,甚至产生发散,而RCS的使用可提高系统稳定性,保证良好的跟踪性能,由此可见,复合控制策略实现了姿态角的精确跟踪。

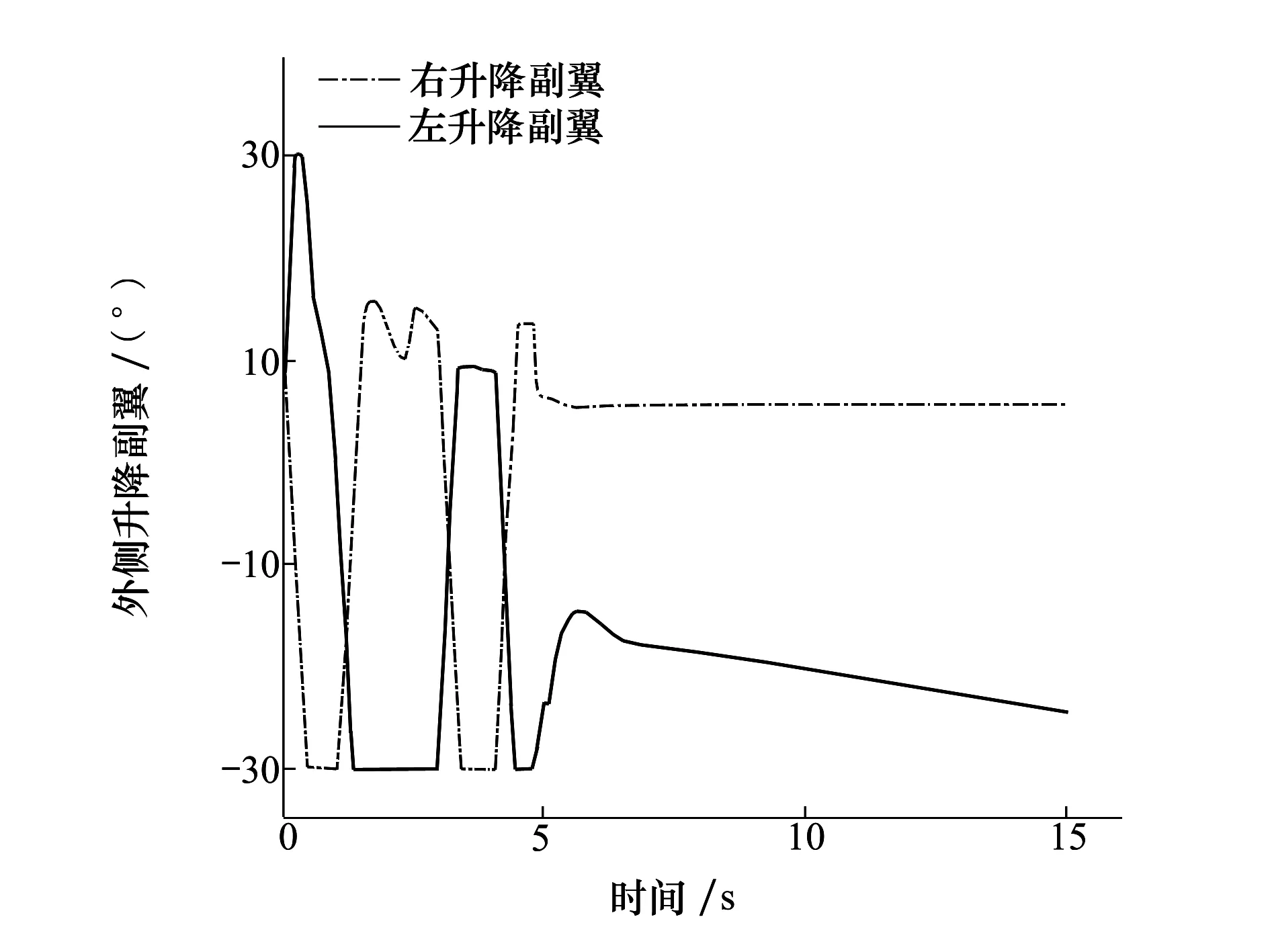
图5 外侧升降副翼偏转

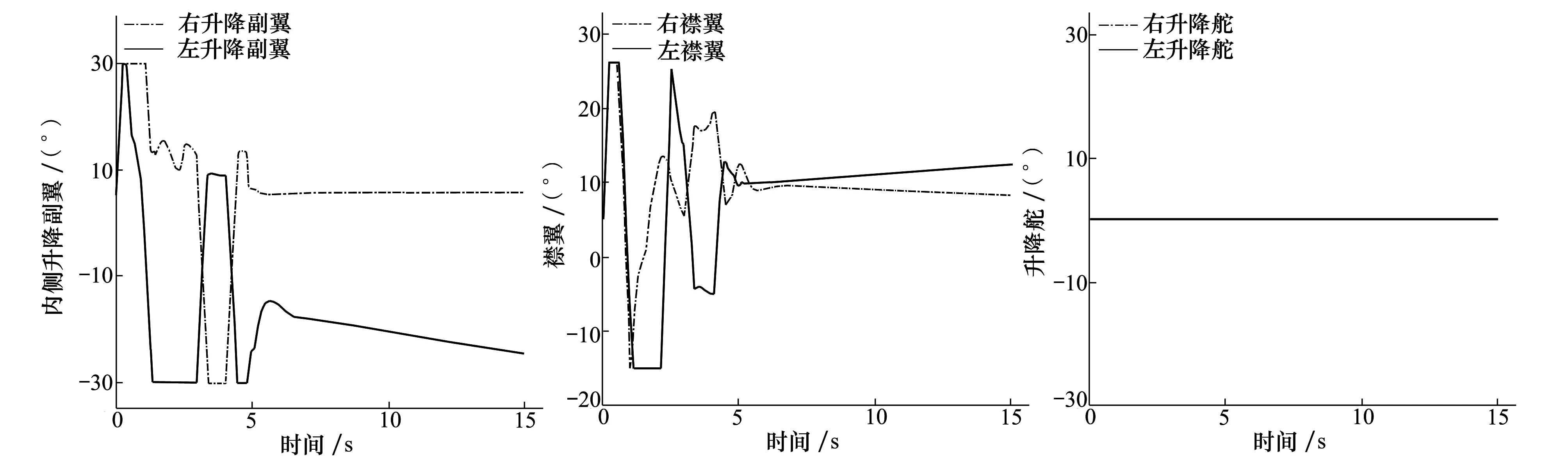
图6 内侧升降副翼偏转 图7 襟翼偏转图8 升降舵偏转

图9 RCS喷头开关状态

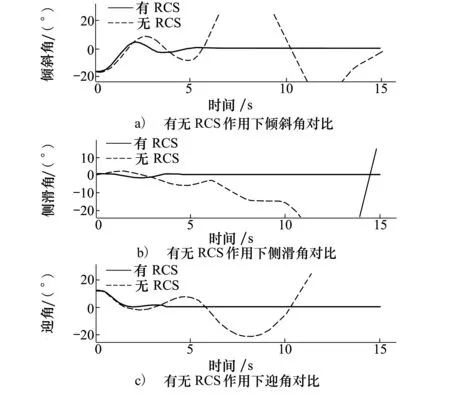
图10 有无RCS作用下姿态角曲线对比

5 结 论

1) 本文针对空天飞行器再入段姿态模型,研究了直接力/气动力复合控制系统有限时间收敛问题。在建立简化ASV数学模型后,提出一种基于RBF神经网络的有限时间滑模控制方法,实现了姿态跟踪误差实际有限时间收敛。

2) 在此基础上,设计了以非线性二次规划和混合整数线性规划实现的气动力/直接力复合控制分配策略,将虚拟控制输入分别映射到气动舵面和直接力装置。

3) 仿真结果说明,该复合控制策略能有效实现姿态角的准确跟踪。