淮河入江水道万福闸站近52年来降雨量变化特征分析

王 江 孙正兰 王骏秋

(江苏省江都水利工程管理处，江苏扬州 225200)

近年来，随着全球气候变暖和人类活动导致一些区域极端气候的发生。降水量异常是引起许多地区旱涝灾害的最主要原因。淮河流域地处中国东部南北气候过渡带，气候复杂，汛期降雨多以暴雨形式出现。本文对万福闸站1966—2017年的降水资料进行分析，得到52年的降水变化特征和趋势预测分析结果，为淮河入江水道尾闾行洪工程的防汛抗旱和科学调度提供决策依据。

1 研究区域概况

万福闸地处扬州市广陵区，位于淮河入江水道廖家沟上，是淮河排洪的主要控制工程之一，主要作用是担负淮河排洪入江水量的65%，引纳江水，改善邵伯湖沿湖地带农田灌溉用水条件，控制扬州段京杭大运河水位，改善通航、城市工业和生活用水条件。该闸共65孔，每孔净宽6m，总长469.2m，总净宽390m，设计流量为8270m3/s。该区域属于亚热带湿润季风气候，四季气候分明，降水集中在夏秋两季，6—7月经常出现连续梅雨天气，7—9月由于受当地台风影响，或者台风与其他天气系统一起遭遇时，常造成淮河地区的特大暴雨。

2 资料来源及分析方法

2.1 资料来源

本文选用万福闸水文站1966—2017年的逐日降水量观测资料，统计出逐月和逐年降水量，其中汛期为每年的5—9月。

2.2 分析方法

降水属非平稳随机水文现象，降水具有趋势性、周期性和平稳随机性等多项特征，所以对降水进行趋势和周期性分析是有必要的。本文采用气象上普遍采用的Mann-Kendall检验法对万福闸站降水进行趋势分析，得出该时期内降水的整体变化趋势和发生突变的年份。对降水周期分析的方法有方差分析法、滑动平均值法、谱分析法和小波分析法，本文采用Morlet小波法对该站降水进行周期性分析，得到降水系列的多时间尺度下的变化周期，从而预测未来的降水趋势。

3 结果及分析

3.1 降水量年内、年际特征

万福闸站降水量年际变化较大，1966—2017年万福闸站的多年平均年降水量为1028.5mm，最大年降水量为1821.5mm，发生年份为2016年；最小年降水量410.8mm，发生年份为1978年；最大年降水量是最小年降水量的4.43倍。

从图1可以看出该站降水量年内季节性变化很大，年内降水量分配不均。全年汛期(5—9月)降水比较集中，汛期降水量达 664.7mm，占年降水量的64.6%；10月至次年4月的降水量为363.8mm，仅占全年降水量的35.4%。连续最大3个月(6—8月)降水量为490.1mm，占全年降水量的47.7%；连续最小3个月(12—2月)降水量为114.8mm，占全年降水量的11.2%。最大月(7月)降水量为201.8mm，占全年降水量的19.6%；最小月(12月)降水量为29.9mm，占全年降水量的2.9%。形成汛期降水量集中、夏涝冬旱的特点。

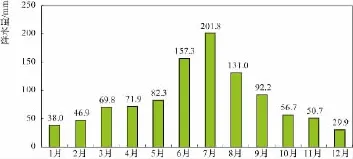
图1 万福闸站月降水量年内分配

3.2 降水量周期变化

小波分析法是一种时频多分辨率分析方法，具有时频局部化功能。小波分析法可以将降水时间系列的频率特征在时间域上展现出来，分析出其主要周期。小波分析法的基本思想是用一簇小波函数系来表示或逼近某一信号或函数。

小波函数ψ(t)连续小波变换后成离散小波变换形式：

式中：Wf(a，b)为小波变换系数；f(t)为一个信号或平方可积函数；a为伸缩尺度；b平移参数的复共轭函数。

将小波系数的平方值在b域上积分，就可得到小波方差，即

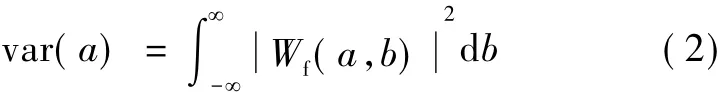
小波系数的模值反映了不同时间尺度变化周期所对应的能量密度，模值越大，说明周期变化越明显。图2为万福闸站年降水量小波系数模等值线图，从图2中可以明显看出20～25年时间尺度的模值最大，10～15年和3～6年时间尺度的周期变化次之。

为进一步分析小波的主周期，可以通过小波方差图分析。图3为万福闸站年降水量小波方差图，从图3中可以明显看出4个较为明显的峰值(23年、14年、10年和4年)。其中，23年时间尺度的周期变化最为明显，为降雨量变化的第一主周期，14年、8年和4年分别对应时间尺度为第二、第三和第四主周期。这个结论与小波系数模等值线图分析的结果是一致的。

通过对图3的分析，可以得到不同主周期特征时间尺度小波实部过程线，见图4。不同时间尺度下的小波系数可反映不同时间尺度下的水文序列变化，正的小波系数对应丰水期，负的小波系数对应枯水期，其中23年、14年主周期特征时间尺度变化最为明显。在23年时间尺度上，流域径流变化的平均周期为15年左右，大约经历了3.5个丰-枯转换期；而在14年时间尺度上，流域的平均变化周期为10年左右，大约5个周期的丰-枯变化。

3.3 降水量变化趋势分析

许多学者不断应用改进的Mann-Kendall方法分析降水、径流、气温和水质等要素时间序列趋势变化。该方法的优点是不一定要满足一定的分布特征，而且不受异常值的扰动，适用于水文时间序列，计算也比较简单。

图2 年降水量小波系数模等值线

图3 年降水量小波方差

图4 不同主周期特征时间尺度小波实部过程线

在Mann-Kendall趋势检验中，假设有n个样本量(x1，…，xn) 的时间序列，对于所有 k，j≤n，且k≠ j，xk和xj的分布是不同的，检验统计量S通过下式计算：

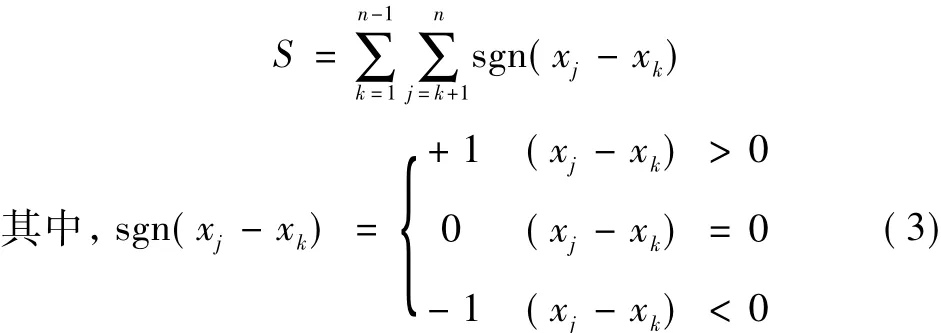
方差var(S)=n(n-1)(2n+5)/18。当 n＞10时，统计值Z计算如下：

统计值Z＞0时，是增加趋势；统计值Z＜0时，则是减少趋势。如果Z的绝对值在大于等于1.28、1.96时，就表示通过了置信度90%和95%的显著性检验。

在Mann-Kendall突变检验中，检验统计量与趋势检验中Z有所不同，通过构造序列

分析绘出的UFk和UBk曲线图。若UFk的值大于0，则表明降水呈上升趋势，反之则表明降水呈下降趋势。如果超过临界线说明变化趋势显著，如果两条曲线相交，则交点为降水变化的突变年份。

在Mann-Kendall趋势检验中，计算得万福闸站S值为 159，var(S)值为 16059，Z 值为 1.25，小于1.28，表明万福闸站52年来降水量呈上升的趋势，但是没有通过置信度90%的显著性检验，说明万福闸站的年降水量增加趋势不明显。

从图5上可以看出，万福闸站年降水量在1969—1975年、1986—2016年呈增加趋势，其他年份呈减少趋势，但都没有通过0.05显著性检验(U0.05=1.96)，说明变化趋势均不明显，根据两条曲线交点的位置，得出万福闸站年降水量在1969年、1973年、1976年、1987年、1991年、1998年、2003年、2008年、2013年存在突变。

图5 万福闸站年降水量UFk和UBk曲线

4 结语

本文通过对万福闸站1966—2017年52年降水量资料的研究，得出入江水道万福闸站多年平均降水量为1028.5mm，全年降水年内分配不均，汛期占了全年降水量的64.6%；降水年际变化具有丰水和枯水年组交替出现的周期性趋势，降水系列存在23年、14年、10年和4年4个多时间尺度的周期变化，其中23年时间尺度的周期变化最为显著，降水变化的平均周期为15年左右，大约经历了3.5个丰-枯转换期。万福闸站52年来降水量整体呈上升的趋势，但年降水量增加趋势不明显。