提升学生数学知识应用能力的策略与实践

☉江苏省南通田家炳中学 张爱华

知识与智能是相互依存、相互制约的.合理地储存和运用知识可以完美展现知识能力，快速提高智能水平.知识的储存可以更好地促进知识的运用，知识的合理运用是对所储存知识效果的一种检测.因此，深度探究影响知识储存和运用的最重要因素，才能真正意义上提升知识储存和运用的效果，培养学生的数学学科核心素养.下面，笔者结合自己的数学课堂教学，谈一谈如何优化学生的知识结构，不断提升学生的知识运用能力.

一、概念和定理教学，应注重知识的条件化培养

课堂教学中，学生借助一系列数学实践活动，获取数学概念和数学定理.不过，怎么利用数学概念、定理去分析和解决数学问题，常常会让学生感觉到困惑，并频频受挫.因此，教师在进行数学概念和定理的教学时，既需引导学生将数学概念、定理和公式这一系列陈述性知识“收入囊中”，更需学生掌握“如果……就……”之类的程序性知识［1］.数学中的概念和定理来源于实际生活，是对实际生活的一种抽象概括，具有条件与范围意义上的局限性.

例如，在教学“平行线”这一内容时，教师给出概念：在同一平面内，不相交的两条直线平行.此处，我们就必须着重强调“在同一平面内”这一限制条件.

要培养学生知识的条件化，教师应注意渗透，将特殊问题中的一般性条件单独抽取，激活学生已有知识，提升运用知识解决实际问题时的通性、通法，获得认识上的提升，促进学生的认知结构不断生长，快速完善，并形成较好迁移［2］.

例如，如果依次将任意一个四边形四条边上的中点连接，那么所得的四边形是什么四边形？我们可以进行以下的变式训练：

变式1：如果依次将一个平行四边形四条边上的中点连接，那么所得的四边形是什么四边形？

还可将此题中的平行四边形进行改变，可以为菱形、矩形、正方形、等腰梯形，想一想：改变之后可得什么四边形呢？

变式2：（1）如果我们想得到的图形为菱形，可以依次连接哪种四边形四条边的中点？

（2）如果我们依次连接某种四边形四条边的中点，得到了一个矩形，那么，这个四边形的对角线需（ ）.

A.相等并且垂直 B.垂直并且平分

C.相互垂直 D.相互平分

变式3：如图1，已知四边形ABCD，其中AC=6，BD=8，AC⊥BD，依次连接四边形ABCD的四条边AB、BC、CD、AD的中点，可以得到四边形A1B1C1D1，接着依次连接四边形A1B1C1D1的四条边的中点，可以得到四边形A2B2C2D2……以此类推，最终得到四边形AnBnCnDn.仔细探讨，并解答：

图1

（1）求最终所得的四边形AnBnCnDn的面积；

（2）求四边形A5B5C5D5的周长.

从以上案例中可以看出，在数学课堂教学中，教师可以不断变换方式去合理运用教学素材，从不同的角度，选用不同的方法，帮助学生逐步走出简单思维的窠臼，通过不断变换方法与范围运用知识，获得认知上的不断提升，加速思维的节奏，在变式中求创新，引导思维结构的发展，让思维具有灵活性、广阔性、延展性，并不断培养学生的数学求异思维.

二、习题教学，应注重知识策略化的培养

所谓的“策略性知识”，就是教会学生学习与思维有关的知识.它位于知识结构的最顶端，是对学生学习和思维的调节.正确把握策略，不但可以将知识运用的范围减小，还可以提升运用的速度.教师在指导时，不仅需将解决问题的方式教给学生，还需培养学生自我调控思维的方式.

解题离不开联想，借助联想可以更好地形成问题与知识之间的联系，从而迁移已有解题经验.不过，如何合理展开联想呢？数学教师可以借助习题教学进行系统指导.

一般意义上来讲，教师进行有策略的教学，首先，需有宽广的数学学科策略，从而实现对其他学科的迁移；其次，需凸显解题时采用的一般策略与重点策略；最后，需注重和具体教学方法相融合.

例1如图2，已知p+q+1＜0，求证：1在x2+px+q=0的两根之间.

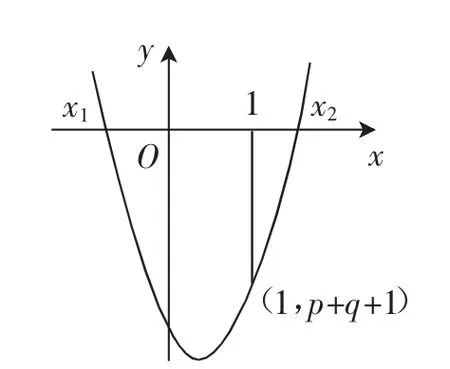
图2

本案例中，如果按照一般解题方法解题，先运用求根公式去求此方程的两个根x1、x2，再进行求证，会陷入解题误区.所以，必须寻求其他的解题思路.

假设y=x2+px+q.显然，此抛物线的开口是向上的.如果x=1，那么y=p+q+1.已知p+q+1＜0，则点（1，p+q+1）位于x轴下方，所以方程有两个根x1和x2，并且1位于这两个根之间.

第二种解题方法显然没有使用一般思维进行思考，而是巧妙使用了图像法，并成功破解难题.

例2三角形三边的长分别为a、b、c，求证：方程b2x2+（b2+c2-a2）x+c2=0根的情况为没有实数根.

本题是融合了代数与几何的一道综合题，从数学实质上来讲，它涉及了一元一次方程、不等式、二次函数等.学生首先需联想什么条件下一元二次方程不存在实数根.此题的本质是需证明题中方程根的判别式Δ=（b2+c2-a2）2-4b2c2＜0成立，并据此去联想因式分解.分解因式后，继续联想三角形三条边之间的关系，据此判别连乘积的符号，最后得证.

在数学解题的过程中，我们采用的基本策略有：列举法、转化法、数形结合、一般与特殊化、整体与局部等.在课堂教学中，教师在进行解题策略的教学时，需做到由简到难，逐步渗透；基于解题策略，精选巧妙案例展示其广泛的应用，激发学生对已学策略的概括性认识；策略传授需注重适时、适量，给予学生充足的消化理解时间.

三、单元教学，应注重知识结构化的培养

每个学生的知识存储结构有所不同，所以在运用效率上也存在一定的差异.假如学生可以在大脑中形成系统的、相关联的，并具有一定结构层次的系统知识，那么在运用的时候就会更灵活、更完善.换句换说，若学生大脑中的知识结构是“零散”“孤立”“碎片”的形式，那么运用起来也是割裂的、困难的.

在课堂教学中，注重知识结构化的培养，教师需立足于一个整体化的高度，将待学知识置于一个系统化的结构框架中，深入分析教材，融通各个知识点之间的关联，不断渗透知识结构上的整体意识.通过教学，将学生头脑中的知识串联成线状，链接成链状，结合成网状，形成系统的网络知识结构.教师在对每个单元进行教学时，引导学生将一些在广泛区域内运用的知识，置于一个更为宽广的区域进行教学，从而串联所有数学知识.

例如，笔者在教学完“二次函数”这个章节之后，带领学生从二次项前面的系数、抛物线开口的方向、对称轴、增减性、顶点坐标、最值等关键要素出发完善“二次函数”的知识结构图，促进知识结构化延展.

实践经验表明，若想培养学生数学知识的结构化，需要教师引导学生学会“融通”不同知识的能力.教师通过数学课堂教学，借助综合练习和一题多解等训练，实现不同知识之间的串联，实现数学知识的纵横联系，互相渗透.在不断的学习中，有效促进学生大脑中知识结构的不断完善和优化，并实现在其他学科中的迁移运用.

总之，数学课堂教学中，数学教师需深度研究教材，借助师生之间的互动，进行教学反馈，将学习策略渗透到各种教学中，不断优化学生的知识结构，提升学生的知识运用能力，发展学生的思维品质，培养学生的数学学科核心素养.