对数学错题集“动手脚”的大胆尝试

☉江苏省如东县茗海中学 栾春秀

困惑：人人都知道数学错题集的重要性，它能够避免错误反复发生，同时能提高复习的针对性，但是，学生做错题集时，有些题目题型相同，错了好多次，次次都抄下来，有些是计算题，也要抄下来，这不是做无用功吗？这样做而得的错题集，对优生还可以，因为他们错得不多，学习负担不重，但对于后进生，他们错得很多，如果一一抄下来，岂不是加重了他们的学习负担？他们为了应付老师的检查乱抄一气，根本起不到反思的作用，而且他们不会认真订正，写出正确答案，对以后的复习也起不到帮助作用.我们搞错题集的目的是把学生一单元测试或一阶段考试的典型错题集中在一起，分析错误原因及共有几种解法等，找出最优解法，写在错题集上，再次遇到这类题型时不要再错，要应用这个知识点，并且到时候不要想不到应用.

我对传统数学错题集“动了手脚”，做了如下一些尝试：

第一，在新授课时，遇到一章节的重要题型，让学生抄在错题集上，或在课堂上讲解，或让学生课后充分思考后，教师再讲解.

例如：已知：如图1，在四边形ABCD中，∠ABC=∠ADC=90°，E、F分别是AC、BD的中点．求证：EF⊥BD．

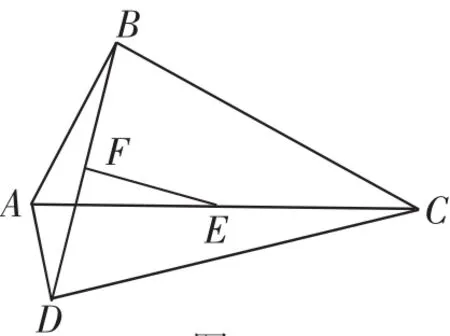
图1

这是利用“直角三角形斜边中线等于斜边一半”这一重要定理的证明题，但学生想不到作辅助线.遇到直角三角形斜边中点这类问题，一般思路是：连接直角顶点与斜边的中点，构成直角三角形斜边上的中线等于斜边的一半这个基本图形.本题中已知F是BD的中点，又要证明EF⊥BD，就要构造等腰三角形，利用等腰三角形三线合一的基本图形，连接BE、DE，即：“要证一条线段是另一条线段的垂直平分线，常构造等腰三角形，用三线合一基本图形”.这两种辅助线非常重要，学生必须掌握.在错题集的错题旁边，要求学生标注：“为什么要作这样的辅助线？作这条辅助线的目的是什么？”，从而使学生能真正理解一题，精通一类.

第二，在做过练习或测验后，通过批改，教师发现学生错题比较多、比较典型时，要求全班每名学生都抄在错题集上.

例如此类题：已知y＝y1+y2，y1与x成正比例，y2与x-2是正比例关系，当x=1时，y=0；当x=-3时，y=4.

（1）求y与x的函数关系式，并说明此函数是什么函数；

（2）当x=3时，求y的值.

本题放在中午作业中让学生独立完成，本人在批改后发现全班只有几个人正确，大部分错在y1与x是正比例的关系上，设y1＝kx，y2与x-2是正比例关系，设y2＝k（x-2），则有y1＝kx+k（x-2）.学生设的比例系数是一样的，而本题的比例系数不一定一样，学生极易出错，于是，本人让学生把此题整理到错题集中，分析错误原因，在错题旁边写出错误原因，并把正确的解题过程写出来，以便下次遇到相同类型的题时不再出错.

第三，在讲评试卷时，有极少一部分题（一套试卷可能只有一道或两道）很难，或有的已经明显超过数学课程标准的要求.如果在班级授课制的大班教学的模式下针对所有学生讲解，就会有一部分学困生听不懂.即使大部分学生听懂了，他们也不一定会应用，只剩下极少一部分优等生能真正理解并掌握应用.曾经有人说过：“学生会做的不讲，学生讲了也不会做的也不讲.”对于这些题目，要求学生抄在错题集上，让优等生课后独立思考或相互间讨论，要求他们做好完整的解题过程，这样在培优补差时教师对优等生单独辅导，教给他们审题、分析、思考的方法，再针对题目引导学生完善拓展.

如下面这类题型：如图2所示，在平面直角坐标系中，有长方形ABCD，定点A、B分别在y轴、x轴上，当点B在x轴上运动时，点A随之在y上轴运动，长方形ABCD的形状一直不变，其中AB＝4，BC＝2，运动过程中，点O到点D的最大距离为__________．

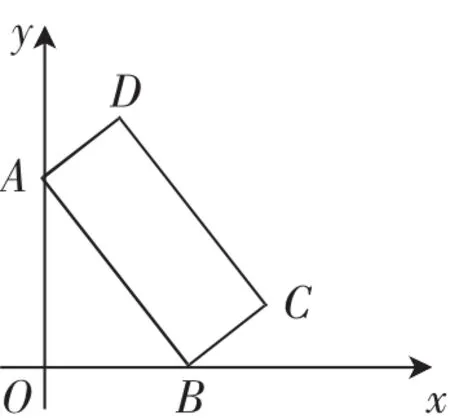
图2

本题很难，要利用三角形的三边关系求最大值，三角形的两边之和大于第三边，当三边在同一直线上时，第三边的最大值是另两边的和，同时要学生构造三角形，构造直角三角形斜边上的中线等于斜边的一半，构造以斜边AB的中点M、O、D为顶点的三角形，学生很难想到，太难了！针对这类题，本人在平时教学中建立错题集时，注意给方法、给思路、给注意点、给切入点等，必要时学生小组间还可以讨论解决.这样通过少量这类题型的训练，学生的能力得到升华，同时有错题集的帮助，学生每隔一段时间翻开来看看，能及时提醒他们.

教师针对第一类和第二类抄在错题集上的题目，在讲评时要注重以下三点：思路分析、解题操作、总结规律.

数学家欧拉曾经说过：“类比就是大胆的创造.”这充分说明类比能力是创新能力的一个重要方面，提高学生的类比能力是提高学生创新能力的一个重要途径.如何培养类比思维？首先，学会用思路分析来搭桥引路，思考问题就具有了大局观和层次性，许多问题能够化繁就简，化难为易.其次，借助板书演绎解题过程，给学生以示范和模仿作用.初中阶段的学生正处在由形象思维向抽象思维过渡的阶段，在解数学题时还存在很大的模仿性.有了教师的解题操作，在解题时要注重步步有据，不要跳步，更不能瞎写一通.再次，总结规律起到画龙点睛作用，做题目时我们要让学生学会“品题”，针对一道题的错误，要从解题方法、解题思路、心理因素等角度全方位、多层面分析原因.对概念不清、运算错误、知识遗忘、粗心大意、逻辑混乱、策略不当等常见原因要有自我反省意识和纠正欲望；对解题过程中产生的根本性的失误，要多从知识架构和知识掌握的牢固程度方面找差距，从而着力解决学生做题过程中出现的“会而不对、对而不全，全而不美”的毛病.对错误原因，要求学生用红笔在错题旁边做标注，以起警示作用.

在错题讲解过程中，更要注重数学思想的渗透，要突出常用的、基本的数学思想，如转化思想、函数和方程思想、数形结合思想、分类讨论思想等，这些思想是知识转化为能力的桥梁，对学生解题能力的形成和提高有很大的推动作用.在引导学生建立数学思想的基础上，需要重点培养学生对各种数学思想的灵活运用能力，在面对某一类型的数学题时，能够快速、准确地选择解决思路与方法，以促进学生思维的灵活性，积累经验，促进学生数学思想应用能力的提升.

在错题集的整理中，需要重点引导学生发现错因，根据错题产生的原因反思其中的思维缺陷，学生坚持不懈地整理错题集，对思维能力、解题能力的提升，必然会起到事半功倍的效果.在大量的实践教学中，我发现很多学生出现错误的原因，大多在于对知识的理解不到位，或是由于审题不仔细，如以下有关一元一次方程的选择题：

下列选项中，是一元一次方程的是（ ）.

在面对这个问题的时候.约90%以上的学生会选取D或无正确选项，大多数学生出现错误的原因在于对一元一次方程定义的理解不深.在错题集整理中发现学生对基础概念性知识的了解不够深入，为了避免在遇到此类问题时出现错误，教师应引导学生重点对一元一次方程定义中的三个主要要素进行剖析.首先，构成一元一次方程需要具备含未知数的项为整式，且分母上不含有未知数；其次，仅含有一个未知数，且简化合并后方程中的未知数不可为0；最后，方程中的未知数次数为1.由此可知，本题的正确答案应该是C.

在错题讲解结束后不能一丢了之，教师要出一些相似的题型让学生练习以起到巩固强化的作用.人的记忆具有规律性.当呈现的信息得到个体的注意，并加以学习之后，短时记忆便形成了，一旦复习没有跟上，短时间内就会遗忘；如果复习跟上了，短时记忆就会转化为长时记忆，所以及时巩固非常有必要.

当然，在抄错题时，如果是比较长的简答题，也可以不让学生抄，把错误题目连同它的错误解题过程剪下来，然后粘贴在错题集上，这也是不错的方法，既节约了时间，同时错的解法又在旁边，能一目了然地知道错误原因，起到提醒自己以后不要再犯同样错误的效果.

如果把初中生的数学错题集以以上的形式呈现，能起到事半功倍的成效.大家不妨来尝试尝试，这能收到不错的教学效果哦！ W