核心素养视角下探讨高中数学懂而不会现象的消减策略
杨长春 冯太平
(宜兴市官林中学 江苏无锡 214251)
一、重视基础,以课本为本,勿随意增加难度
在实际教学过程中,教师一定要认真地研读课标要求、仔细地揣摩课本上每节课的重点、难点,切勿随意增加难度或拔高要求。若教师对课标要求理解不到位或者对课本重难点把握不准确,在上课过程中难免会出现随意增加难度或者重难点讲解不到位的现象,这样就会导致学生“懂而不会”。
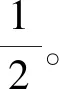
(1)求a、b的值;
(2)求函数y=f(x)的单调区间;
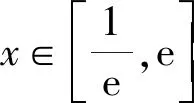
变式:已知实数a>0,函数f(x)=ax3-4ax2+4ax(x∈R)。
(1)求函数f(x)的单调区间;
(2)若函数f(x)有极大值16,求实数a的值。
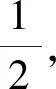
数形结合法在求解函数单调性的相关题目时可以起到事半功倍的效果。在解题结束后,教师应该给学生留有一定的时间进行独自思考、消化,接着,再变式让学生独自完成,并给以相应点评,这样可以最大限度地消减“懂而不会”现象。
二、重视学生已有的基础,从学生的视角分析问题
学生在学习过程中出现“懂而不会”现象的原因之一就是学生对于题目所表达的意思不十分了解,因此教师应“俯下身子”,从学生的思维水平、思考角度出发,选择适合学生理解水平的题目,在讲解解题方法的时候注意与学生的生活实际相联系,在课堂上将学生放在主体地位,注重与学生之间的互动。教师在课堂上除了要选择合适的教学内容作为例题进行讲解,还要联系数学课本的体系及新课标的具体要求对学生真实的学习能力进行考量,挑选与学生密切相关且容易理解的题目,特别是选择一些学生感兴趣的例题,尽可能缓减学生在解题时的畏难情绪,调动学生对数学学习的积极性。
案例2:在数列{an}中,a1=1且3an+1=1-an。
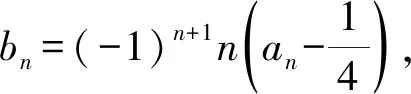
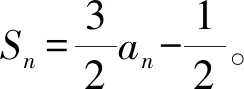
(1)求数列{an}的通项公式;
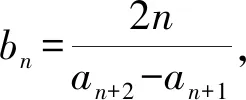
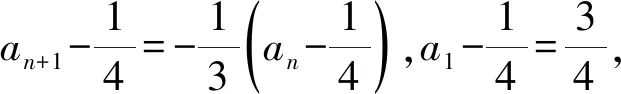
“错位相减法”是求一个等差数列{an}和一个等比数列{bn}对应项的乘积构成的数列{anbn}的前n项和Tn的常用方法。平时教学过程中,部分学生的思维水平较高,基础较好,擅于钻研,一听就懂,对于每一步骤不但知其然且知其所以然;但也有部分同学相反,他们基础较弱,对教师上课讲的每一步都能听懂,但是对每一步的原理并不懂,所以他们看似懂了,实则不会,故而在做题时不是系数错,就是符号错,甚至项数出错。因此,教师在讲解过程中应多考虑基础薄弱的学生,引导学生探究解法,在黑板上板演详细的解答过程,同时特别强调该方法的关键就是“错位”。在解题结束后,教师应给学生留足时间进行独自思考、消化,从根本上理解“错位”的含义及作用,接着,再变式让学生独自完成,并给以相应点评,进一步加深理解。
三、重视思想方法的渗透,一题多法、一题多变
在高中数学的课堂上一定要注重对解题思想方法法渗透,注重引导学生去思考知识体系之间的联系,帮助学生建构知识网络。有些教学难点要善于利用数式、图形在不同的数学分科中的不同含义与等价形式,把一个分科里的公式、定理、方法和技巧巧妙地迁移到另一个分科中,达到化繁为简、化难为易的目的。 同时能够拓展学生的思维的广度与深度,一定程度上激发了学生的学习热情,很大程度上能够减少“懂而不会”的现象。
案例3:已知x≥0,y≥0,x+y=4,求x2+y2的取值范围。
变式1:已知x≥0,y≥0,x2+y2=4,求x+y的取值范围。
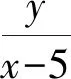
本题采用减元法、换元法、几何法都能解决。
高中数学的课堂中,针对一体多法的题目,在遵循学生认知规律的前提下,展示学生的思维过程很重要,适时点拨,注重总结归纳,让学生思维的触角向各个方向伸展,并建构新的知识网络。这同时要求教师不能团于思维定式,从多种角度考虑问题,具有广泛的思维空间,从尽可能多的方法中择优选用,从而培养学生思维的创新性和发散性。
在数学教学过程中,变式是必不可少的,变式是为了巩固所学,减少“懂而不会”现象,在课堂上教师讲解的变式不应太难,应有针对性、典型性,这在复习课上尤为重要,让学生在“变”中体会“不变”的本质,使学生体会这些题目中体现的共同数学思想或使用的数学方法。
“教无定法,贵在得法。”在教与学的过程中,老师是学生与知识之间的纽带,在自身专业素质够硬的前提下,还要多听听来自学生的声音。影响“懂而不会”的因素还有很多,具体措施需要我们在实践中不断探索、完善。

