基于量纲分析的非充分采动导水裂缝带高度预测
娄高中,郭文兵,2,高金龙
基于量纲分析的非充分采动导水裂缝带高度预测
娄高中1,郭文兵1,2,高金龙3
(1. 河南理工大学能源科学与工程学院,河南 焦作 454000;2. 煤炭安全生产河南省协同创新中心,河南 焦作 454000;3. 平煤股份一矿,河南 平顶山 467000)
为准确预测非充分采动导水裂缝带高度,选取开采厚度、煤层埋深、工作面倾斜长度、煤层倾角、覆岩力学性质、覆岩结构特征为非充分采动导水裂缝带高度主要影响因素。采用量纲分析建立了导水裂缝带高度与,,,,间的无量纲关系式。结合30组实测数据,采用多元回归得到无量纲关系式的最优函数关系式。选取2个非充分采动工作面导水裂缝带现场实例对预测模型进行了工程验证,预测模型预测结果与实测结果吻合良好,其相对误差分别为3.64%和2.93%,预测模型的预测精度可以满足煤矿安全生产现场需要。
非充分采动;导水裂缝带高度;量纲分析;多元回归
随着我国煤炭资源的高强度开采以及浅部煤炭资源的逐步枯竭,开采深度以8~12 m/a的速度增加,东部矿井更是达到10~25 m/a。随着开采深度的增加,工作面倾斜长度与开采深度之比即采动系数不断减小,当采动系数小于1.2时,工作面为非充分采动,当采动系数小于1/3时,工作面为极不充分采动,此时地表任意点的下沉值均未达到该地质采矿条件下的最大值[1-2]。非充分采动工作面上覆岩层移动和破坏稳定后,按破坏程度分为垮落带、裂缝带和弯曲下沉带,其中垮落带和裂缝带合称为导水裂缝带。导水裂缝带高度是煤矿保水开采、防水安全煤岩柱留设和瓦斯抽采的重要参数,因此,准确确定非充分采动工作面导水裂缝带高度对于煤矿安全生产具有重要意义。目前,非充分采动导水裂缝带高度计算常用方法有理论分析、现场实测、相似模拟、数值模拟等[3-6]。其中,现场实测结果最为可靠,但工作量大,成本较高;理论分析往往对实际情况进行了理想简化,适用性不强;数值模拟和相似模拟中岩体力学参数难以准确确定,模型建立与简化因人而异,计算结果更适合定性分析。
量纲分析,是物理领域中建立数学模型的一种方法。对于某些复杂研究问题,往往难以建立数学模型从而采用数学方程准确表述,或者方程求解过程复杂,不方便在实际中应用,采用量纲分析可以明确各物理量对研究问题的影响作用,在数学上给出各物理量之间明确的函数关系式。非充分采动导水裂缝带高度受多种因素影响,与影响因素之间存在复杂、难定量的非线性关系,因此笔者把量纲分析引入到非充分采动导水裂缝带高度计算中,考虑导水裂缝带高度主要影响因素,根据不同矿区导水裂缝带高度实测数据,采用多元回归分析,建立基于量纲分析的导水裂缝带高度预测模型,为非充分采动导水裂缝带高度预测提供了方法和参考。
1 非充分采动导水裂缝带高度影响因素
导水裂缝带高度影响因素众多,根据理论分析、现场实测、相似模拟、数值模拟等方法对非充分采动导水裂缝带高度的研究,非充分采动导水裂缝带高度主要影响因素包括:开采厚度、煤层埋深、工作面倾斜长度、煤层倾角、覆岩力学性质和覆岩结构特征。
a.开采厚度
开采厚度是导水裂缝带高度的主要影响因素,“三下”开采规范中的经验计算公式[7]中导水裂缝带高度仅与开采厚度有关。当其他条件一定时,薄煤层单层开采或厚煤层第一分层开采时,导水裂缝带高度与开采厚度近似呈线性关系;厚煤层分层开采及综放开采时,导水裂缝带高度与开采厚度近似呈分式函数关系。中硬覆岩条件下导水裂缝带高度与开采厚度间的回归公式[8-9]为

b. 煤层埋深
当煤层埋深为25~2 700 m时,铅直应力基本上等于上覆岩层的重力。因此铅直应力随着煤层埋深的增大而增加,煤层开采后上覆岩层破坏程度越剧烈,导水裂缝带发育高度越大。导水裂缝带高度与煤层埋深间的回归公式[10-11]为
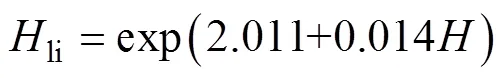

式中为预计导水裂缝带高度范围内硬岩厚度与预计导水裂缝带高度的比值[12]。
c.工作面倾斜长度
工作面基本顶断裂前可视为由煤壁和边界煤柱支撑的固定梁,工作面的倾斜长度越大,基本顶向下弯曲的程度越大,断裂后形成的导水裂缝带高度越大。在覆岩破坏未达到充分采动时,导水裂缝带高度随着工作面倾斜长度的增加而增加,当覆岩破坏达到充分采动后,不再受工作面倾斜长度的影响。导水裂缝带高度与工作面倾斜长度间的回归公式[12-13]为

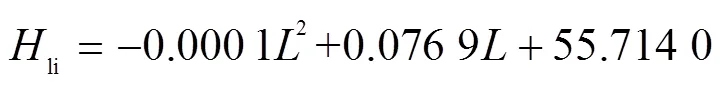
d. 煤层倾角
煤层倾角影响导水裂缝带的形态和高度。对于水平及缓倾斜煤层、倾斜煤层和急倾斜煤层,导水裂缝带在倾斜方向上的形态分别为马鞍形、抛物线形、椭圆形。当煤层倾角小于45°时,导水裂缝带高度随着煤层倾角增大而增大;当煤层倾角为45°~ 60°时,导水裂缝带高度随着倾角的增大而减小[9]。导水裂缝带高度与煤层倾角间的回归公式[9]为

e. 覆岩力学性质与结构特征
“三下”开采规范中,根据覆岩的单向抗压强度,将覆岩力学性质分为坚硬、中硬、软弱和极软弱4类。受采动影响后,坚硬和中硬覆岩易产生裂隙而下沉量较小,覆岩断裂后裂隙不易闭合和恢复其原有隔水能力;软弱和极软弱覆岩不易产生裂隙而下沉量较大,覆岩断裂后裂隙容易闭合并恢复其原有隔水能力。因此,覆岩越坚硬,导水裂缝带高度越大。按从直接顶到基本顶的顺序,导水裂缝带高度范围内的覆岩结构特征可以分为坚硬—坚硬、坚硬—软弱、软弱—坚硬、软弱—软弱4种类型。一般情况下,导水裂缝带高度由小至大对应的覆岩结构特征分别为软弱—软弱、坚硬—软弱、软弱—坚硬、坚硬—坚硬,在定量分析中分别量化取值0.2,0.4,0.6,0.8[14-15]。导水裂缝带高度与覆岩结构特征间的回归公式[16-17]为


2 非充分采动导水裂缝带高度的量纲分析预测模型建立
2.1 量纲分析
量纲分析,是在理论分析和实验的基础上,利用物理量量纲提供的信息,根据量纲齐次原则确定物理量之间关系,在此基础上根据物理原理构建各物理量之间的方程,然后建立数学模型进行求解。运用量纲分析研究非充分采动导水裂缝带高度的具体步骤如下[18-19]:


根据式(10),非充分采动导水裂缝带高度li可以表示为

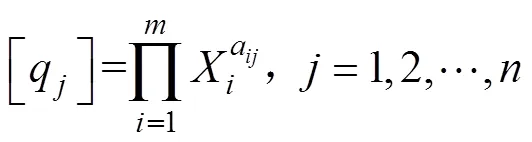
物理量的基本量纲只有7个,对于纯力学类问题仅涉及3个基本量纲:质量、长度和时间,分别用M、L、T表示。则物理量q的量纲又可以表示为
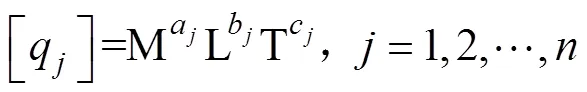
导水裂缝带高度属于力学类问题,因此式(11)中的7个物理量均为基本量纲M、L、T的组合,根据式(13),7个物理量的量纲见表1。
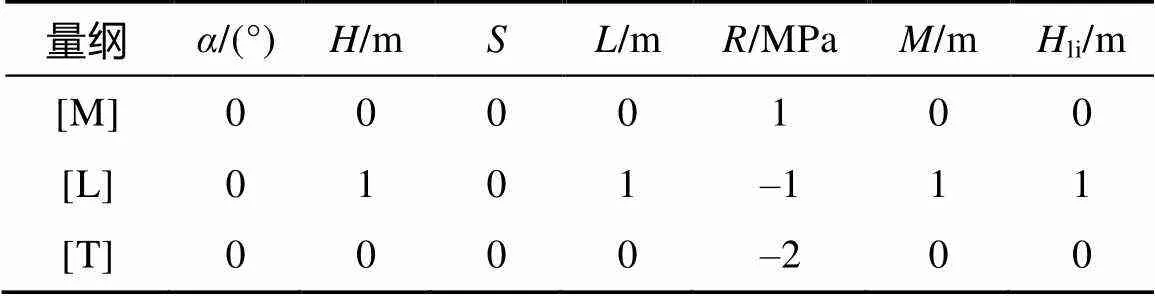
表1 物理量量纲
根据表1,量纲矩阵形式为:

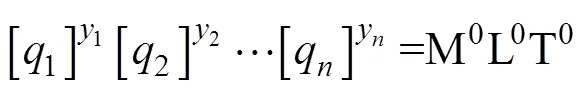
展开式(15)可以得到



式(14)中量纲矩阵的秩rank()为2,因此=0有5个基本解:1=(1,0,0,0,0,0,0)T,2=(0,0,1,0, 0,0,0),3=(0,–1,0,1,0,0,0),4=(0,–1,0,0,0,1,0),5= (0,–1,0,0,0,0,1)T。

根据量纲矩阵的基本解计算结果,无量纲量计算结果见表2。

表2 无量纲量π计算结果

非充分采动导水裂缝带高度函数式(11)的无量纲表达式为

2.2 非充分采动导水裂缝带高度多元回归分析
非充分采动导水裂缝带高度的无量纲表达式(19)中的函数形式未定,为了得到非充分采动导水裂缝带高度定量预测模型,采用多元回归方法进行分析。多元回归分析的基本模型为
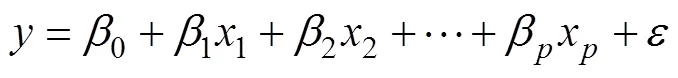

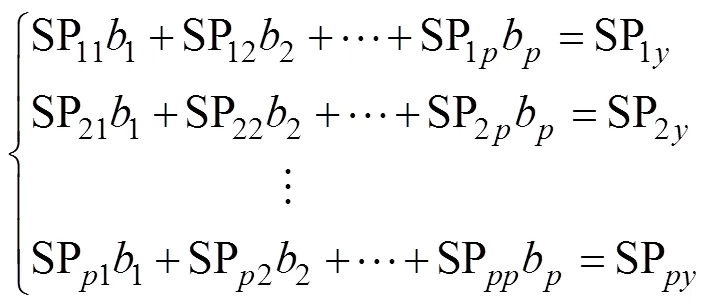

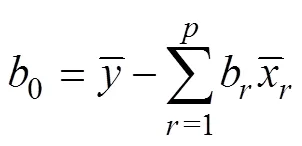
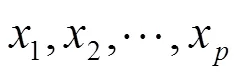
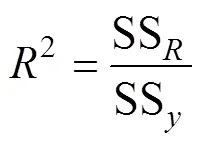

实际问题研究中,因变量与自变量之间除了线性关系外还存在非线性关系,常见的多元非线性关系有多元幂函数、多元对数函数和多元指数函数。非线性函数可以变换为线性形式后按照线性回归进行求解。
根据相关文献收集了我国部分矿区非充分采动导水裂缝带高度实测数据[20-21],见表3。根据表3中实测数据,采用Matlab软件,分别用多元线性函数、多元幂函数、多元对数函数和多元指数函数对导水裂缝带高度无量纲表达式(19)进行了回归分析,通过比较相关系数2和误差平方和SSE确定最优函数关系式,2越大,SSE越小,相应的函数关系式最优。4种函数回归计算结果见表4,从表4中可以看出,多元线性函数的相关系数2最大,误差平方和SSE最小,多元线性函数为最优函数关系式。因此,基于量纲分析的非充分采动导水裂缝带高度预测模型为

式(25)适用于非充分采动工作面导水裂缝带高度计算,即工作面倾斜长度与煤层埋深之比小于1.2的情况。从式(25)可以看出,非充分采动导水裂缝带高度与覆岩结构特征、煤层倾角、工作面倾斜长度与煤层埋深之比、开采厚度与煤层埋深之比、煤层埋深有关。
3 工程验证
为了进一步检验基于量纲分析的非充分采动导水裂缝带高度预测模型的可靠性和适用性,选择济宁三号煤矿1301、新集一矿1303两个非充分采动工作面进行现场工程验证。
济宁三号煤矿1301工作面开采3下煤,煤层厚度为3.46~7.84 m,平均厚度为6.3 m;煤层倾角为0°~ 10°,平均倾角为4°。工作面走向长度为1 614.8 m,倾斜长度为170 m,开采深度为445~515 m,平均开采深度为480 m。覆岩结构特征为坚硬—软弱型。工作面采用综采放顶煤开采,全部垮落法管理顶板。将以上地质与采矿参数带入非充分采动导水裂缝带高度预测模型式(25)中,1301非充分采动工作面导水裂缝带高度预测值为71.1 m,根据井下钻孔法现场实测确定的导水裂缝带高度为68.6 m[22],预测模型预测值与现场实测值的绝对误差为2.5 m,相对误差为3.64%。
新集一矿1303工作面开采13-1煤,煤层厚度为6.64~10 m,平均厚度为7.76 m;煤层倾角为6°~10°,平均倾角为8°;工作面走向长度为645 m,倾斜长度为134 m,开采深度为323~335 m,平均开采深度为329 m,覆岩结构特征为软硬—坚硬型。工作面采用综采放顶煤开采,全部垮落法管理顶板。将以上地质与采矿参数带入非充分采动导水裂缝带预测模型式(25)中,1303非充分采动工作面导水裂缝带高度预测值为86.4 m,根据地面钻孔冲洗液漏失量法现场实测确定的导水裂缝带高度为83.94 m[23]。预测模型预测值与现场实测值的绝对误差为2.46 m,相对误差为2.93%。

表3 非充分采动导水裂缝带高度实测数据

表4 多元函数表达式
济宁三号煤矿1301工作面和新集一矿1303工作面的工程验证结果表明,基于量纲分析的非充分采动导水裂缝带高度预测模型是可行的,其预测精度能够满足煤矿现场安全生产需要,可以为煤矿保水开采、防水安全煤岩柱留设和瓦斯抽采提供参考。
4 结论
a. 通过现场实测、理论分析、相似模拟、数值模拟等方法,确定非充分采动导水裂缝带高度的主要影响因素为开采厚度、煤层埋深、工作面倾斜长度、煤层倾角、覆岩力学性质、覆岩结构特征。
b. 基于量纲分析,建立了非充分采动导水裂缝带高度与煤层倾角、覆岩结构特征、工作面倾斜长度、煤层埋深、开采厚度之间的无量纲表达式。根据非充分采动导水裂缝带高度实测数据,采用多元回归分析得到了无量纲表达式的最优函数关系式。
c.选取济宁三号煤矿1301工作面和新集一矿1303工作面导水裂缝带高度现场实例对基于量纲分析的非充分采动导水裂缝带高度预测模型进行了工程验证,预测模型预测结果与现场实测结果的绝对误差分别为2.5 m和2.46 m,相对误差分别为3.64%和2.93%,预测精度可以满足煤矿现场安全生产需要,为非充分采动导水裂缝带高度预测提供了方法和参考。
[1] 郭文兵,谭志祥,柴华彬,等. 煤矿开采损害与保护[M]. 北京:煤炭工业出版社,2013:7–37.
[2] 郭增长,韩六合,邓智毅,等. 极不充分开采地表移动和变形特征[J]. 矿山测量,2002(2):55–57. GUO Zengzhang,HAN Liuhe,DENG Zhiyi,et al. Surface movement and deformation characteristics under super- subcritical mining[J]. Mine Surveying,2002(2):55–57.
[3] 施龙青,辛恒奇,翟培合,等. 大采深条件下导水裂隙带高度计算研究[J]. 中国矿业大学学报,2012,41(1):37–41. SHI Longqing,XIN Hengqi,ZHAI Peihe,et al. Calculating the height of water flowing fracture zone in deep mining[J]. Journal of China University of Mining & Technology,2012,47(1):37–41.
[4] 谭毅,郭文兵,杨达明,等. 非充分采动下浅埋坚硬顶板“两带”高度分析[J]. 采矿与安全工程学报,2017,34(5):845–851. TAN Yi,GUO Wenbing,YANG Daming,et al. Analysis on height of “two zones” under subcritical mining in shallow coal seam with hard roof[J]. Journal of Mining & Safety Engineering,2017,34(5):845–851.
[5] 李超峰,虎维岳,王云宏,等. 煤层顶板导水裂缝带高度综合探查技术[J]. 煤田地质与勘探,2018,46(1):101–107. LI Chaofeng,HU Weiyue,WANG Yunhong,et al. Comprehensive detection technique for coal seam roof water flowing fractured zone height[J]. Coal Geology & Exploration,2018,46(1):101–107.
[6] 冯洁,王苏健,陈通,等. 生态脆弱矿区土层中导水裂缝带发育高度研究[J]. 煤田地质与勘探,2018,46(1):97–100. FENG Jie,WANG Sujian,CHEN Tong,et al. Height of water flowing fractured zone of soil layer in the ecologically fragile mining area[J]. Coal Geology & Exploration,2018,46(1):97–100.
[7] 国家安全监管总局、国家煤矿安监局、国家能源局、国家铁路局. 建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范[M]. 北京:煤炭工业出版社,2017:55–56.
[8] 孙亚军,徐智敏,董青红. 小浪底水库下采煤导水裂隙发育监测与模拟研究[J]. 岩石力学与工程学报,2009,28(2):238–245. SUN Yajun,XU Zhimin,DONG Qinghong. Monitoring and simulation research on development of water flowing fractures for coal mining under xiaolangdi reservoir[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(2):238–245.
[9] 尹尚先,徐斌,徐慧,等. 综采条件下煤层顶板导水裂缝带高度计算研究[J]. 煤炭科学技术,2013,41(9):138–142. YIN Shangxian,XU Bin,XU Hui,et al. Study on height calculation of water conducted fractured zone caused by fully mechanized mining[J]. Coal Science and Technology,2013,41(9):138–142.
[10] 马志伟,叶义成,王其虎,等. 含钒页岩矿床开采导水裂隙带发育高度研究[J]. 金属矿山,2013(4):142–146. MA Zhiwei,YE Yicheng,WANG Qihu,et al. Study on height of water flowing fractured zone in containing vanadium shale deposit[J]. Metal Mine,2013(4):142–146.
[11] 张宝安,李佳音,卢洋,等. 采空区覆岩导水裂隙带高度预计方法对比分析[J]. 中国地质灾害与防治学报,2016,27(2):132–136. ZHANG Baoan,LI Jiayin,LU Yang,et al. Comparison and analysis of the prediction method of water flowing fractured zone height[J]. The Chinese Journal of Geological Hazard and Control,2016,27(2):132–136.
[12] 胡小娟,李文平,曹丁涛,等. 综采导水裂隙带多因素影响指标研究与高度预计[J]. 煤炭学报,2012,37(4):613–620. HU Xiaojuan,LI Wenping,CAO Dingtao,et al. Index of multiple factors and expected height of fully mechanized water flowing fractured zone[J]. Journal of China Coal Society,2012,37(4):613–620.
[13] 李培现,谭志祥,顾伟,等. 基于FLAC的导水断裂带分布规律模拟研究[J]. 煤炭科学技术,2015,43(4):31–34. LI Peixian,TAN Zhixiang,GU Wei,et al. Simulation study on distribution law of water flow crack zone based on FLAC[J]. Coal Science and Technology,2015,43(4):31–34.
[14] 康永华,申宝宏. 水体下采煤宏观分类与发展战略[M]. 北京:煤炭工业出版社,2017:177–184.
[15] 李振华,许延春,李龙飞,等. 基于BP神经网络的导水裂隙带高度预测[J]. 采矿与安全工程学报,2015,32(6):905–910. LI Zhenhua,XU Yanchun,LI Longfei,et al. Forecast of the height of water flowing fractured zone based on BP neural networks[J]. Journal of Mining & Safety Engineering,2015,32(6):905–910.
[16] 黄欢,姬亚东. 运用偏最小二乘回归法计算导水裂缝带高度[J]. 矿业安全与环保,2017,44(1):40–44.HUANG Huan,JI Yadong. Application of partial least squares regression for calculating height of water flowing fractured zone[J]. Mining Safety & Environmental Protection,2017,44(1):40–44.
[17] 赵高博,郭文兵,杨达明,等. 综放开采覆岩破坏模型及导水裂隙带高度研究[J]. 中国安全科学学报,2017,27(11):144–149. ZHAO Gaobo,GUO Wenbing,YANG Daming,et al. Study on overburden failure models and height of water flowing fractured zone in fully mechanized caving mining[J]. China Safety Science Journal,2017,27(11):144–149.
[18] 赵国彦,梁伟章,王少锋,等. 基于量纲分析的巷道围岩松动圈预测模型[J]. 岩土力学,2016,37(增刊2):273–278. ZHAO Guoyan,LIANG Weizhang,WANG Shaofeng,et al. Prediction model for extent of excavation damaged zone around roadway based on dimensional analysis[J]. Rock and Soil Mechanics,2016,37(S2):273–278.
[19] 岳哲,叶义成,王其虎,等. 基于量纲分析的岩石相似材料抗压强度计算模型[J]. 岩土力学,2018,39(1):216–221. YUE Zhe,YE Yicheng,WANG Qihu,et al. A model for calculation of compressive strength of rock-like materials based on dimensional analysis[J]. Rock and Soil Mechanics,2018,39(1):216–221.
[20] 胡炳南,张华兴,申宝宏. 建筑物、水体、铁路及主要井巷煤柱留设与压煤开采指南[M]. 北京:煤炭工业出版社,2017:172–180.
[21] 王正帅,邓喀中,谭志祥. 导水裂缝带高度预测的模糊支持向量机模型[J]. 地下空间与工程学报,2011,7(4):723–727. WANG Zhengshuai,DENG Kazhong,TAN Zhixiang. Height prediction of water fractured zone based on fuzzy SVM[J]. Chinese Journal of Underground Space and Engineering,2011,7(4):723–727.
[22] 黄福昌,倪兴华,张怀新,等. 厚煤层综放开采沉陷控制与治理技术[M]. 徐州:中国矿业大学出版社,2007:119–120.
[23] 刘谊,朱林,金吕锋. 新集矿区推覆体水文工程地质条件研究和水害防治实践[M]. 徐州:中国矿业大学出版社,2008:50–65.
Prediction of the height of water flowing fractured zone under subcritical mining based on dimensional analysis
LOU Gaozhong1, GUO Wenbing1,2, GAO Jinlong3
(1. School of Energy Science and Engineering, Henan Polytechnic University, Jiaozuo 454000, China; 2. Coal Production Safety Collaborative Innovation Center in Henan Province, Jiaozuo 454000, China; 3.No.1Coal Mine, Pingdingshan Coal Mining Co. Ltd., Pingdingshan 467000, China)
In order to accurately predict the height ofwater flowing fractured zone under subcritical mining, mining thickness, mining depth, inclined length of working face, dip angle of coal seam, overburden mechanical properties, overburden structure characteristicswere selected as the main influencing factors on the height of water flowing fractured zone under subcritical mining. Dimensionless relations between the height of water flowing fractured zone and,,,,were established by dimensional analysis. Based on 30 sets of measured data, the optimal function relation of dimensionless relation was obtained by multiple regression. The prediction model is validated with field examples from two subcritical working faces, the prediction values are in good agreement with the measured values, and the relative errors are 3.64% and 2.93% respectively, the prediction accuracy of the prediction model can meet the field requirements of safe production in coal mine.
subcritical mining; height of water flowing fractured zone; dimensional analysis; multiple regression
National Natural Science Foundation of China(51774111);Excellent Talents of Science & Technology Innovation in Henan Province(184200510003)
娄高中,1988年生,男,河南平顶山人,博士研究生,从事“三下”采煤研究.E-mail:754937725@qq.com
娄高中,郭文兵,高金龙. 基于量纲分析的非充分采动导水裂缝带高度预测[J]. 煤田地质与勘探,2019,47(3):147–153.
LOU Gaozhong,GUO Wenbing,GAO Jinlong. Prediction of the height of water flowing fractured zone under subcritical mining based on dimensional analysis[J]. Coal Geology & Exploration,2019,47(3):147–153.
1001-1986(2019)03-0147-07
TD823.83
A
10.3969/j.issn.1001-1986.2019.03.023
2018-07-18
国家自然科学基金项目(51774111);河南省科技创新杰出人才资助项目(184200510003)
(责任编辑 张宏 周建军)

