两种结构小直径TP2铜管爆破压力的同质性
杨 帆 刘 岑 张红卫 刘 兵 范有雄 刘小宁
(1.武汉软件工程职业学院 机械工程学院 湖北 武汉:430205;2.湖北轻工职业技术学院 机电工程学院 湖北 武汉:430070)
在食品、医药、卫生、医疗领域以及工业与民用热交换器中,经常采用外直径为Φ7.00~Φ12.70的小直径软态TP2铜管输送有一定工作压力的液体或气体;为保证铜管强度的安全,计算其爆破压力必须准确。
铜光管与铜内螺纹管是小直径软态TP2铜管常见的两种结构,这两种结构铜管爆破压力的同质性,是指在相同条件时,其爆破压力试验数据的波动在允许范围内,并能真实反映软态TP2铜材相应性能的性质。显然,同质性不但是两种结构铜管爆破压力能否采用同一公式计算的前提[1-3],而且还是两种结构铜管爆破压力概率分布分析的基础[4-8]。目前尚未见到对不同结构小直径软态TP2铜管爆破压力同质性的研究。
文中以外直径为Φ7.00~Φ12.70的小直径TP2铜光管与铜内螺纹管为研究对象,分别将其实测爆破压力与中径公式计算值之比视为随机变量,基于27组不同结构铜管实测爆破压力[3]的有效性分析[9-11],应用概率论与数理统计理论方法[12-13],研究了两种结构小直径TP2铜管爆破压力的同质性。
1 基本理论与方法
1.1 具有统计性质随机变量的构建
1.1.1 小直径TP2铜管爆破压力计算公式
假设小直径软态TP2铜光管与铜内螺纹管的爆破压力具有同质性,对于爆破压力不受端部结构影响的长铜管[14-16],用中径公式计算其爆破压力[3]:
(1)
式中,u为铜管爆破压力的中径公式计算值,MPa;Rm为铜材抗拉强度的均值,MPa;K为铜管径比的均值,K=D0/Di;Di、D0分别为铜管内、外直径的均值,mm。
1.1.2 构建具有统计性质的随机变量
构建如下具有统计性质的随机变量
(2)
式中,p为小直径TP2铜管爆破压力的实测值,MPa;r为具有统计性质的的随机变量。
1.2 统计量及其有效性
通过试验可得到相同结构小直径TP2铜管爆破压力的n组实测数据pi(1≤i≤n),根据式(1)可得到爆破压力的中径公式计算值ui(1≤i≤n),对应的统计量由式(2)可得:
(3)
式中,ui为采用中径公式算得的第i个小直径TP2铜管爆破压力,MPa;pi为第i个小直径TP2铜管爆破压力的实测值,MPa;ri为统计量。
对n组爆破压力实测数据进行统计,可得到统计量的平均值与精密度:
(4)
(5)

应用数理统计中的t分布是判别统计量有效性的基本方法[9-11],在双侧置信度为(1-α)时,由t分布性质和实测数据组数n,可确定判别统计量有效性的t分布系数tn-1,0.5α,文中所用的t分布系数见表1[12-13]。

表1 有关分布系数
判别ri有效性的指标为[14-17]:
(6)
若
|ti|>t0.5α,n-1
(7)
表明ri不是有效统计数据,需要剔除;应从统计数据ri的最小值或者最大值开始剔除无效数据,每剔除1个无效数据,都必须计算其余数据的平均值与精密度,再判别其余数据的有效性;若有m个有效数据,则最后按式(4)与式(5),重新计算m个有效数据的平均值与精密度。
若
|ti| (8) 表明ri是有效统计数据。 文中取α=0.05,即在双侧置信度为95%时分析统计量的有效性,表明有95%把握认为剔除的无效数据是意外因素影响而形成的。 对于小直径软态TP2铜光管(结构A),具有统计性质的随机变量 式中,pA为小直径软态TP2铜光管(结构A)实测爆破压力,MPa;u为采用中径公式算得的小直径TP2铜光管(结构A)爆破压力,MPa。 通过试验,如果获得小直径软态TP2铜光管(结构A)爆破压力pA的nA组有效试验数据pAi(i=1,2,…,nA),不难得到pA的统计量: 式中,pAi为小直径软态TP2铜光管的第i个有效实测爆破压力,MPa;uAi为采用中径公式算得的小直径TP2铜光管的第i个爆破压力,MPa;rAi为小直径TP2铜光管的第i个爆破压力与中径公式计算值之比。 对nA组有效实测爆破压力数据进行统计,可得到统计量的平均值与精密度: (9) (10) 对于小直径软态TP2铜内螺纹管(结构B),具有统计性质的随机变量 式中,pB为小直径软态TP2铜内螺纹管(结构B)实测爆破压力,MPa;uB为采用中径公式算得的小直径TP2铜内螺纹管(结构B)爆破压力,MPa。 通过试验,如果获得小直径软态TP2铜内螺纹管(结构B)爆破压力pB的nB组有效试验数据pBi(i=1,2,…,nB),不难得到pB的统计量: 式中,pBi为小直径软态TP2铜内螺纹管的第i个有效实测爆破压力,MPa;uBi为采用中径公式算得的小直径TP2铜内螺纹管的第i个爆破压力,MPa;rBi为小直径TP2铜内螺纹管的第i个爆破压力与中径公式计算值之比。 对nB组有效实测爆破压力数据进行统计,可得到统计量的平均值与精密度: (11) (12) 假设rA与rB都是基本符合正态分布的随机变量,其均值分别为μA与μB,标准差分别为σA与σB。小直径软态TP2铜光管(结构A)爆破压力与铜内螺纹管(结构B)爆破压力同质性的判据为: μA≈μB,σA≈σB (13) 即rA与rB的均值与标准差分别无显著差异。 1.3.1 标准差无显著差异的判别 数理统计中的F分布,是比较标准差σA与σB是否存在显著差异的工具,比较依据为[17-18]: (14) 若 F1-0.5α,nA-1,nB-1≤F≤F0.5α,nA-1,nB-1 (15) 表明在双侧置信度为(1-α)时的标准差σA≈σB,即标准差σA与σB无显著差异。 其中 取α=0.02,文中所用的F分布系数见表1[12-13]。 1.3.2 均值无显著差异的判别 数理统计中的t分布也是比较均值μA与μB是否存在显著差异的工具。假设σA≈σB,则均值μA与μB是否存在显著差异的比较依据为[17]: (16) 其中 (17) 若 |t|≤tnA+nB-2,0.5α (18) 表明在双侧置信度为(1-α)时的μA≈μB,即均值μA与μB无显著差异。 取α=0.02,文中所用的t分布系数见表1[12-13]。 1.3.3 评价 当均值μA与μB和标准差σA与σB满足式(13)时,表明rA与rB概率分布相同,rA与rB的分布规律一样和分布参数相同,即小直径软态TP2铜光管与铜内螺纹管的爆破压力具有同质性。 由以上分析可知,可将小直径软态TP2铜光管与铜内螺纹管的有效爆破压力合并,研究随机变量r的概率分布,概率分布包括两个内容,一是分布规律,二是分布参数。 1.4.1 分布规律 基于合并的同质性试验数据,可采用假设检验的方法[17-19],分析随机变量r的分布规律。 1.4.2 分布参数 ①均值的取值区间。双侧置信度为(1-α)时,r的均值μ的取值区间为: μ∈[μmin,μmax] (19) 其中 (20) (21) 式中,μmin与μmax分别为均值μ在双侧置信度为(1-α)时的下限与上限;t0.5α,n-1为t分布系数,由自由度(n-1)与0.5α查得。 本文取α=0.02,所用的t分布系数见表1。 ②标准差的取值区间。双侧置信度为(1-α)时,r的标准差σ取值范围为: σ∈[σmin,σmax] (22) 其中 (23) (24) 本文取α=0.02,所用的χ2分布系数见表1。 ③变异系数的取值范围。双侧置信度为(1-α)时,r的变异系数C取值范围为: C∈[Cmin,Cmax] (25) 其中 Cmin=σmin/μmax,Cmax=σmax/μmin (26) 式中,Cmin与Cmax分别为C在双侧置信度为(1-α)时的下限与上限。 有关单位利用材质为软态TP2、外直径为Φ7.00~Φ12.70、径比为1.0601~1.1724的不同结构铜管进行室温液压爆破试验。 对于小直径软态TP2铜光管,获得15组爆破压力试验数据,现将爆破试验数据列入表2,表2中序号12~15的铜光管爆破口出现在钎焊处。现将与爆破试验数据pAi及统计值rAi也列入表2。对于小直径软态TP2铜内螺纹管,获得了12组爆破压力试验数据pBi,现将其及统计值rBi列入表3。 表2 铜光管(A)爆破压力试验数据与统计量 表3 铜内螺纹管(B)爆破压力试验数据与统计量 取试验数据有效性的双侧置信度为95%时,对于15组铜光管试验数据,统计值的最小值为表2中序号第15的试验数据r15=0.7242,用式(3)与式(4) 可知判据|t15|= 2.397>t14,0.025=2.145,因此,第15号数据无效。对余下14组铜光管统计值重新计算平均值与精密度,统计值的最小值是表2中序号为第14的试验数据r14=0.7496,再次用式(3)与式(4)可知,|t14|=2.992>t13,0.025=2.160,因此,序号为14的数据无效。对其余的13组铜光管统计值再次计算平均值与精密度,用式(3)与式(4)可知,13组试验数据统计值均有|ti| 表4 铜光管(A)统计量的平均值与精密度 对于表3中序号为1~12的12组铜内螺纹管试验数据,统计值的最小值是序号为第12的试验数据r12=0.8240,用式(3)与式(4)可知判据|t12|=2.612>t11,0.025=2.201,因此,第12组数据无效。对余下的11组铜内螺纹管试验数据再次计算平均值与精密度,用式(3)与式(4)可知,表3中序号为1~11的11组试验数据统计值均有|ti| 表5 铜内螺纹管(B)统计量的平均值与精密度 研究表明,钎焊加热可使焊缝附近的铜管材料退火,严重时会产生过热和过烧,导致铜管爆破压力降低[3];文中剔除的是3组爆破压力过低的无效数据,笔者认为是过热和过烧造成的,因此,过热和过烧导致铜管爆破压力降低的现象,应引起学术界与工程界的高度重视。 对于小直径软态TP2铜光管与铜内螺纹管,其有效爆破压力的统计值见表4与表5,由式(14)可得到标准差的比较依据: 根据表1,F0.99,12,10=0.206,F0.01,12,10=5.11,显然F满足式(15),即0.206≤F≤5.11,表明在双侧置信度为98%时标准差σA≈σB,即σA与σB无显著差异。 由于σA与σB无显著差异,由式(17)可得: =0.04220 由式(16)可得到均值的比较依据: 根据表1,t0.02, 22=2.183,显然t满足式(18):|t|=0.2834 根据以上分析,在双侧置信度为98%时,有μA≈μB与σA≈σB,满足式(13),即rA与rB具有相同的概率分布,故小直径软态TP2铜光管与铜内螺纹管的爆破压力具有同质性。因此,采用中径公式计算铜光管与铜内螺纹管的爆破压力合适。 从以上分析还可知,与铜光管相比,内螺纹对小直径软态TP2铜管爆破压力的影响不明显。 分布规律假设检验的基本方法见[4-8,19-23]。 4.1.1rA与rB的分布规律 ①假设随机变量rA与rB基本符合正态分布。rA与rB分别有13组与11组有效统计数据,因1+3.3lg13= 4.67与1+3.3lg11=4.44,故将其分别分为5个区间。 ②计算皮尔逊统计量之和。rA与rB每个区间实际频数与理论频数差异的皮尔逊统计量之和见表6。 表6 rA与rB的皮尔逊统计量 ③检验。由于rA与rB的自由度都为f=5-1-2=2,取显著度δ=0.05,皮尔逊统计量的允许值由表1得: 4.1.2 r的分布规律 ①同质性有效数据的合并。由于小直径软态TP2铜光管与铜内螺纹管的有效爆破压力是同质的,因此,可将铜光管与铜内螺纹管有效爆破压力的统计值合并,见表7。 表7 铜光管与铜内螺纹管统计量的平均值与精密度 4.2.1rA的分布参数 双侧置信度为98%时,基于表4数据,由式(19)~式(21)可得rA均值μA的取值区间: μA∈[0.9428,1.0120] (27) 由式(22)~式(24)可得rA标准差σA的取值范围: σA∈[0.02652,0.07186] (28) 将式(18)与式(19)代入式(25)与式(26),可得rA变异系数CA的取值范围: CA∈[0.02621,0.07622] (29) 4.2.2rB的分布参数 双侧置信度为98%时,基于表5数据,由式(19)~式(21)可得rB均值μB的取值区间: μB∈[0.9367,1.0279] (30) 表8 r的皮尔逊统计量 由式(22)~式(24)可得rB标准差σB的取值范围: σB∈[0.02989,0.09002] (31) 将式(18)与式(19)代入式(25)与式(26),可得rB变异系数CB的取值范围: CB∈[0.02907,0.09611] (32) 4.2.3r的分布参数 双侧置信度为98%时,基于表7数据,由式(19)~式(21)可得r均值μ的取值区间: μ∈[0.9641,1.0083] (33) 由式(22)~式(24)可得r标准差σ的取值范围: σ∈[0.03153,0.06373] (34) 将式(18)与式(19)代入式(25)与式(26),可得r变异系数C的取值范围: C∈[0.03127,0.06610] (35) 4.2.4 关于分布参数的讨论 根据以上分析,随机变量rA与rB具有同质性,但是,从式(27)~式(35)可知,rA与rB的分布参数取值区间存在一些差别,可认为这是有效试验数据的差异造成的。另外,利用两个正态随机变量分布参数的比较方法[20],可知随机变量rA与rB的分布参数取值区间无显著差异。 由于随机变量rA与rB具有同质性,将其有效试验数据合并,得到随机变量r的分布参数取值区间,比较式(27)~式(35),即分析rA、rB与r分布参数的取值区间,可以发现r分布参数的取值区间是最优的。 应用数理统计理论与方法,建立了小直径软态TP2铜光管与铜内螺纹管爆破压力同质性的分析方法,基于24组有效实测爆破压力数据,得到如下结论。 1)不考虑端部结构的影响,文中两种结构小直径软态TP2铜光管与铜内螺纹管的爆破压力具有同质性,内螺纹对小直径软态TP2铜管爆破压力的影响不明显,可用中径公式计算铜光管与铜内螺纹管的爆破压力。 2)在显著度为0.05时,小直径TP2铜管24组有效爆破压力的实测值与中径公式计算值之比,是基本符合正态分布的随机变量;在双侧置信度98%时,该随机变量的均值位于0.9641与1.0083之间,标准差位于0.03153与0.06373之间,变异系数位于0.03127与0.06610之间。1.3 不同结构铜管爆破压力的同质性
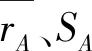

1.4 概率分布

2 试验数据与统计量的有效性


2.1 铜光管

2.2 铜内螺纹管

3 同质性分析
3.1 标准差
3.2 均值
3.3 同质性评价
4 概率分布
4.1 分布规律




4.2 分布参数

5 结论

