捆绑火箭超静定连接结构参数化建模与优化

蒋国庆，陈万华，王元兴

(中国空气动力研究与发展中心设备设计及测试技术研究所，绵阳621000)

1 引言

助推器能够大幅度提高火箭的运载能力，各航天大国相继在各自的运载火箭系列的基础上开发出了捆绑式运载火箭[1]。 助推器与火箭芯级之间一般采用静定式连接，也有采用超静定连接方式。 超静定连接结构设计与刚度相关，且在一定程度上影响了火箭的动特性[2]。 为实现火箭结构轻量化，提高火箭运载能力，有必要对超静定连接结构进行优化设计。

随着计算机技术和结构优化设计方法的不断发展，基于参数化模型和智能优化算法的联合优化方法得到了越来越广泛的研究和使用[3]。 参数化建模的应用范围十分广泛，目前主要研究方向是参数化造型[4]。 主流CAE 软件的二次开发功能可以实现参数化建模，主要的二次开发工具有ANSYS 的APDL 语言[5]、ABAQUS 的Python语言[6]和MSC.PATRAN 的PCL 语言[7]等。 智能优化算法包括遗传算法、模拟退火算法等，其中遗传算法是模仿自然界生物进化机制而发展起来的随机全局搜索和优化方法[8-9]，使用尤其广泛。 本文采用PCL 语言建立捆绑火箭超静定连接结构的参数化模型，并结合遗传算法对其进行优化设计。

2 有限元模型

某捆绑火箭主要由芯级和四个助推器组成，按常规梁单元建模，即以站点为节点，将箭体质量分布在各节点处并在节点处建立相应的质量单元(MASS 单元)，而节点与节点之间则用无质量梁单元连接。 芯级与助推器之间的连接结构对火箭的动特性有重要影响，需要采用合理的方法对其进行模拟。

捆绑连接结构由前捆绑、中捆绑和后捆绑组成，其中前捆绑和中捆绑均采用大刚度梁单元(CBEAM 单元)连接捆绑火箭芯级梁、助推器中心梁梁上和箭体周边的连接点，以此模拟火箭连接处的刚性面，采用杆单元(CROD 单元)模拟芯级与助推器之间的连杆，同时利用CBEAM 单元和CROD 单元之间自由度的不匹配关系来模拟连杆端点处的铰接效果。 后捆绑连接处为一球铰，在此采用RBE2 单元进行模拟，释放其3 个转动自由度。 这样助推器与芯级之间形成超静定结构，且每个助推器与芯级之间均为一次超静定。

超静定捆绑火箭梁模型及其三维显示图如图1 所示。

3 参数化建模

图1 捆绑火箭梁模型及其三维显示图Fig.1 Beam model and its 3D display of strap-on launch vehicle

火箭的捆绑连接结构比较复杂，且质量较重，通过对其进行优化设计可以减轻重量。 采用遗传算法对捆绑连接结构进行优化设计前，需要得到捆绑连接结构的参数化模型。

3.1 参数选取

根据独立性原则和完备性原则，设置优化参数见表1，各参数位置见图2。

表1 捆绑连接结构选用参数统计表Table 1 Main parameters of connection structure

3.2 参数化建模

在创建火箭有限元梁模型的过程中，软件会自动生成记录历史建模命令的model＿name.db.jou文件。 提取该文件中的建模命令并把预先设定的参数或参数表达式代替相应建模命令中的数据，即可得到捆绑火箭的参数化模型。

4 结构优化设计

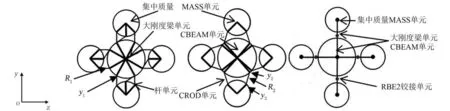
图2 捆绑火箭捆绑连接结构Fig.2 Connection structure of strap-on launch vehicle

对火箭中的超静定连接结构进行优化设计时，把设计变量设置为各连杆的位置坐标及各连杆的外径；考虑到火箭第一阶自振频率对火箭动特性的重要性，在此把性能约束条件设置为火箭第一阶自振频率要求不能低于某一数值；考虑到加工可行性和结构协调性，在此把几何约束条件设置为各连杆的位置坐标和各连杆的外径只能在一定范围内变动。 从而，捆绑火箭连接件的优化模型可以描述为式(1)：

优化设计方法有多种，如传统的线性规划法、无约束优化方法、约束优化方法、离散设计变量优化方法等。 本次优化设计中各连杆的具体坐标和各连杆的外径与火箭的动特性(如自振频率等)之间的关系很复杂，无法推导出其显示表达式，因此难以采用传统优化算法解决此问题。 而启发式算法如遗传算法、模拟退化算法等能够很好得解决此问题。 本文采用遗传算法对捆绑连接结构进行优化设计，计算流程[4]如图3 所示。

本次优化设计中捆绑连接结构5 个参数的变化范围如表2 所示。 遗传算法的运行参数设置为群体规模为60，迭代次数为40，基于MATLAB、MSC.PATRAN 以及MSC.NASTRAN 的联合优化设计流程如图4 所示。

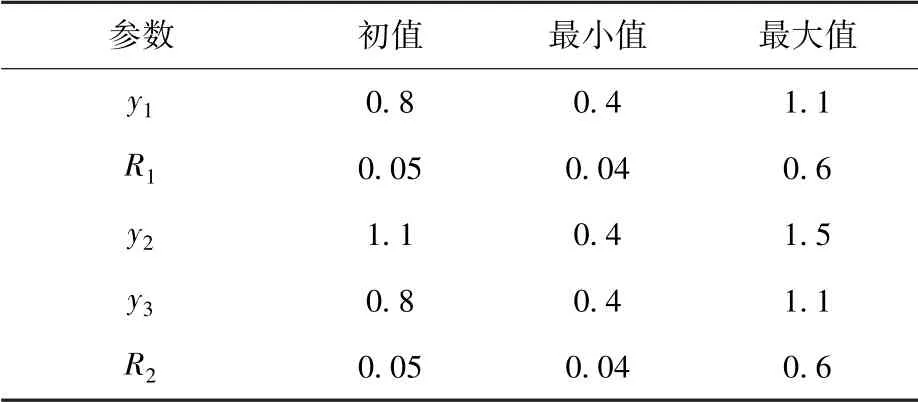
表2 各参数变化范围Table 2 Range of parameters/m

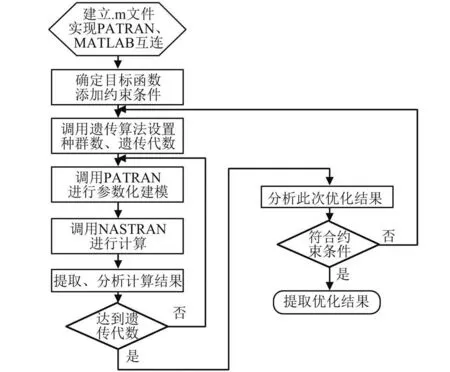
图4 捆绑火箭连接件优化设计流程Fig.4 Optimization process of connection structure

遗传算法的计算历程如图5 所示。 由图可知，连杆总质量随着迭代次数的增加，先急剧下降，后变得非常平缓，说明此次优化设计收敛性较好，连杆总质量在第40 代时得到了最优值。 各参数的优化结果如表3 所示。 优化后火箭前捆绑、中捆绑连接形式如图6 所示。 由表3 和图6 可知，优化后模拟火箭刚性面的大刚度梁单元之间的夹角明显减小，同时前捆绑和中捆绑连杆外径均有所减小。

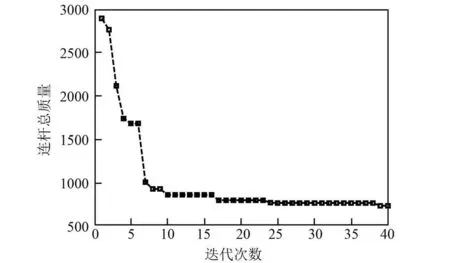
图5 遗传算法的迭代计算过程Fig.5 Iterative computation process of GA

表3 优化前后各设计变量数值对比表Table 3 Comparison of variables before and after optimization/m

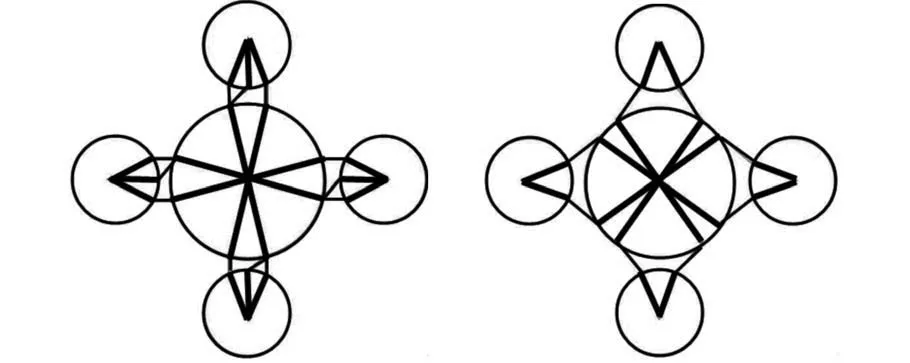
图6 优化后前、中捆绑连接结构示意图Fig.6 Schematic diagram of main connection structure after optimization

优化后连杆总质量及捆绑火箭第一阶自振频率如表4 所示。

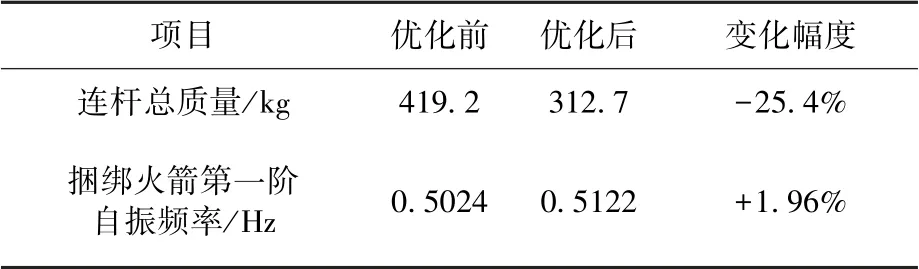
表4 优化前后连杆总质量和捆绑火箭第一阶自振频率对比表Table 4 Comparison of total quality and first order frequency before and after optimization

由表4 可知，优化后连杆总质量比优化前连杆总质量减少了25.4%，主要是由两个方面造成：①连杆位置的改变导致了连杆长度的缩短；②前捆绑、中捆绑连杆的外径分别减少了12.8%、3.2%。 优化后捆绑火箭的第一阶自振频率比优化前只上升了1.96%，这主要是由于连杆总质量在捆绑火箭总质量中所占的比重较小。 综上可知，优化后，捆绑火箭的弯曲基频有所增加，捆绑火箭连杆总质量降幅显著，达到了预期目的。 但评论本次优化结果的有效性还需比较优化前后火箭动特性和连杆内力。

5 优化前后捆绑火箭对比

5.1 优化前后动特性分析

对优化前后捆绑火箭分别进行自由状态下的模态分析，得到第一阶弯曲和第一阶扭转模态及所对应的自振频率对比如表5 所示。

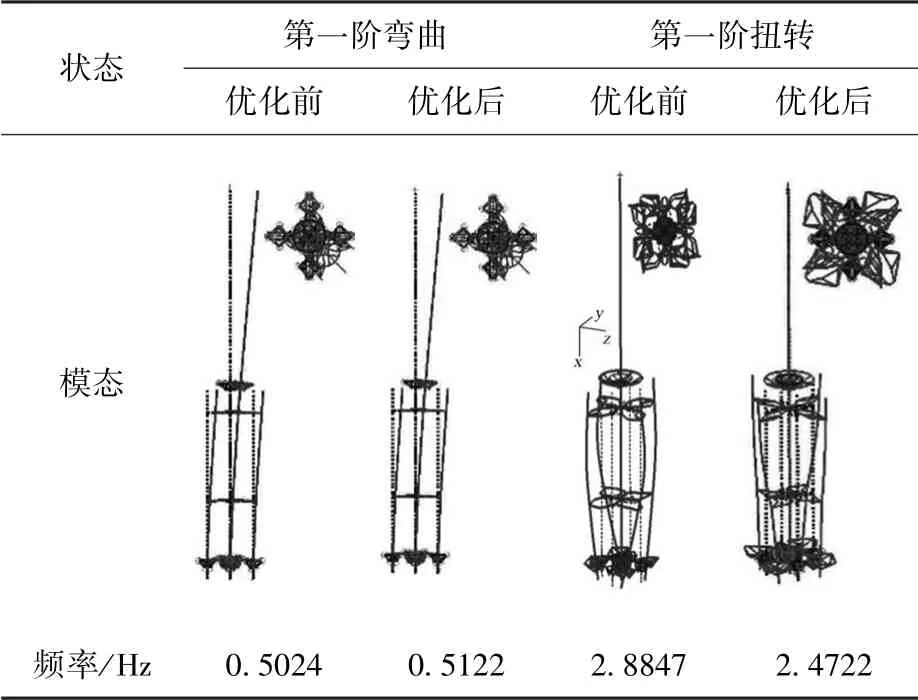
表5 优化前后捆绑火箭自振频率和模态对比表Table 5 Comparison of frequency and modes before and after optimization

由表5 可知，优化后的扭转基频比优化前降低了14.3%。 说明在保持连杆数量和连杆连接方式的前提下，连杆的位置和连杆的外径使得捆绑火箭的扭转基频变化较大，而对捆绑火箭的弯曲基频影响不大。

5.2 优化前后捆绑火箭连杆载荷分析

捆绑火箭起飞前竖立在发射台上，只受重力作用，边界条件为火箭芯级底部固支。 此种工况下优化前后捆绑火箭连杆最大内力及后捆绑主接头各向最大节点力对比表如表6 所示。

表6 优化前后捆绑火箭连杆载荷对比表Table 6 Comparison of load in connective rods before and after optimization/N

由表6 可知，优化后连杆的最大内力较优化前增加较多，这主要是由于优化后连杆位置发生变化所致。 优化前后捆绑火箭后捆绑主接头的各向最大节点力相差不大，部分方向的节点力得到了改善。

综上可知，优化后捆绑火箭的动特性和连杆载荷情况都有了一定的改善。

6 结论

1)利用CBEAM 单元和CROD 单元之间自由度的不匹配关系能够很好得模拟连杆端点处的铰接效果。

2)采用PCL 语言和遗传算法能够对捆绑火箭超静定连接结构进行优化设计，且优化效果比较明显，其中连杆总质量减小了25.4%，火箭弯曲基频基本保持不变，火箭扭转基频减小了14.3%，连杆所受载荷得到一定改善。

参考文献(References)

[1]康开华，才满瑞，尚辉.质子号运载火箭及其运营[J].导弹与航天运载技术， 2006， 3(283)： 21-27.Kang K H，Cai M R，Shang H.Proton launch vehicles and its operation[J].Missile and Space Vehicle，2006，3(283)：21-27.(in Chinese)

[2]李家文.大型捆绑火箭姿态控制系统的建模、设计与分析[D].长沙： 国防科学技术大学， 2011.Li J W.Modeling， Design and Analysis of Large Strap-on Vehicle's Attitude Control System[D].Changsha： National University of Defense Technology， 2011.(in Chinese)

[3]麻越垠，陈万华，王元兴，等.基于响应面方法的叶栅摆动装置有限元模型修正[J].振动与冲击， 2016， 35(22)：232-236.Ma Y Y， Chen W H， Wang Y X， et al.Finite element model updating of the blade swing mechanism based on response surface method [J].Journal of Vibration and Shock， 2016， 35(22)： 232-236.(in Chinese)

[4]李磊.基于结构完整性分析的固体火箭发动机药形改进与优化设计[D].长沙： 国防科学技术大学， 2011.Li L.Improvement and Optimization Design of Solid Rocket Motor based on Structural Integrity Analysis[D].Changsha：National University of Defense Technology， 2011.(in Chinese)

[5]师访.ANSYS 二次开发及应用实例详解[M].北京： 中国水利水电出版社， 2012： 17-34.Shi F.Second Development and Application Example of ANSYS[M].Beijing： China Water ＆ Power Press， 2012： 17-34.(in Chinese)

[6]苏景鹤， 江丙云.ABAQUS Python 二次开发攻略[M].北京： 人民邮电出版社， 2016： 12-14.Su J H， Jiang B Y.Second Development Strategy of ABAQUS Python[M].Beijing： Posts ＆ Telecom Press， 2016： 12-14.(in Chinese)

[7]李磊， 唐国金， 段静波， 等.基于参数化建模的车轮形药柱形状优化[J].国防科技大学学报， 2011， 33(1)： 11-16.Li L， Tang G J， Duan J B， et al.Shape optimization of wheel shape grain based on parameterized modeling[J].Journal of National University of Defense Technology， 2011， 33(1)：11-16.(in Chinese)

[8]刘翔春， 廖瑛， 文援兰.应用改进遗传算法优化天基光学监视平台轨道[J].国防科技大学学报，2014，36(3)：58-62.Liu X C， Liao Y， Wen Y L.Applying the improved genetic algorithm to optimize the orbit for space-based optics surveillance platform[J].Journal of National University of Defense Technology， 2014， 36(3)： 58-62.(in Chinese)

[9]宋春生， 于传超， 张锦光， 等.基于遗传算法的复杂双层磁悬浮精密隔振系统LQR 控制研究[J].振动与冲击，2016， 35(16)： 99-105.Song C S， Yu C C， Zhang J G， et al.LQR Control of a Complex Two-stage Magnetic Suspension Active Precise Isolation System based on Genetic Algorithm[M].Journal of Vibration and Shock， 2016， 35(16)： 99-105.(in Chinese)