一种微重力下洗衣装置的设计与研究

汤凯利，张 华，邓德喜，章松发

(无锡小天鹅股份有限公司， 无锡214028)

1 引言

长期多人载人飞行任务中，航天员的衣物如果继续采用一次性服装，会因为补给和运输而造成较大的资源消耗。 为了更环保并且能够经济高效地解决该问题，需要设计一种微重力环境下可用的洗衣装置，实现衣物的洗净与循环使用。

微重力环境下，地面上现行的洗涤方法主要有以下问题：①手洗无法实现密封和自动化；②波轮自动洗衣机，借助离心力产生的水与衣物的作用力将衣物洗净，无法实现密封；③滚筒自动洗衣机，借助离心力将动能转化为势能，然后自由落体，利用摔打将衣物洗净，借助了重力。 因此需要设计一种密封良好，不利用重力的洗衣装置，在微重力下将衣物洗净。

本文提出一种具有柔性洗涤袋，同时柔性袋被凸包夹持挤压且被齿轮结构驱动的洗衣装置。由于创造微重力环境进行测试代价高昂且周期较长，为了衡量该洗衣装置的洗涤力度，提升其洗净能力，引入仿真模型指导设计和优化。 应用光滑粒子动力学法(SPH)与有限单元法(FEM)耦合方法模拟洗衣装置的洗涤过程。 结合所提出的洗净经验公式，用该模型指导洗衣装置的结构和动力优化设计。

2 基本设计

为实现密封良好，且有效提供机械力的洗涤方式，微重力下洗衣装置的关键结构设计如图1所示。 图中略去了管道等组件，仅示意了实现洗涤功能的3 个主要结构，分为柔性袋组件、导轨组件和凸包组件。 其中柔性袋组件由PP 材料框架与硅橡胶片组成，可密封容纳衣物与水；导轨组件位于柔性袋上下两侧，用齿轮齿条结构实现驱动，可带动柔性袋组件左右往复运动；凸包组件分为前端凸包和后端凸包，固定于机器外壳上，可在柔性袋左右往复运动时，提供挤压力。 因整机体积限制，柔性袋组件的最大运动行程为100 mm，见图2。 所设计洗涤过程为：先放入衣物与洗涤剂，接着将柔性袋抽真空，然后进水，最后启动导轨，开始洗涤。 洗涤过程中，袋内衣物将在机械力与洗涤剂共同作用下，将衣物洗净。 其中机械力来源包括：柔性袋左右往复运动产生的衣物与水流的摩擦力、衣物与柔性袋PP 材料框架的撞击力以及衣物被凸包挤压的挤压力。

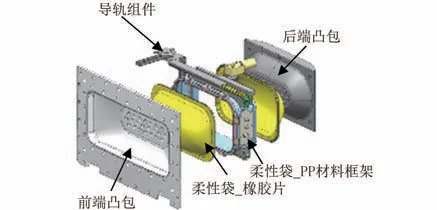
图1 关键结构爆炸图Fig.1 The exploded view of the main structures

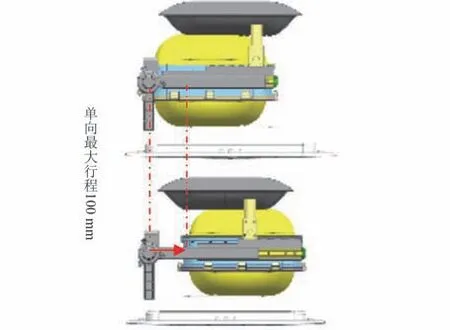
图2 装置最大行程示意图Fig.2 The maximum stroke of the device

洗衣装置初版样机测试结果显示衣物洗净比明显低于国标，根据洗净经验公式，洗净参数由机械力、衣物摔打翻滚频率以及效率共同决定，如式(1)所示：

其中I 为洗净参数，f 为洗涤过程机械力，n为衣物摔打频率，m 为衣物翻滚频率，j 为衣物翻滚效率。 本文针对洗涤过程机械力进行研究，并以滚筒洗净参数为目标，对当前装置结构和运动参数进行优化，以提升装置洗净能力。

3 数值仿真

3.1 理论基础

衡量洗涤力度的仿真模型，需考虑袋内内容物与柔性袋不断撞击挤压这一洗涤过程，是1 个局部存在大变形的模拟问题。 SPH-FEM 耦合方法，能够同时发挥SPH[1]计算大变形和FEM[2]计算精度高计算效率高的优势，十分适用于该类模型内局部出现大变形的问题。 SPH-FEM 耦合方法由Attaway 等[3-4]首先提出，Sonia 等[5]在此基础上发展了1 种SPH-FEM 连续混合方法，根据再生阶数要求，提供多种插值函数及其导数，能够确保SPH 和FEM 的可再生性、收敛性和稳定性。SPH-FEM 耦合在液体晃动、金属切削、冲击爆炸等方面都有应用[6-7]。

3.1.1 模拟流体的SPH 方程

流体控制方程由为不可压黏性Navie-Stokes方程(简称N-S 方程)，即连续方程和动量方程。受重力作用的连续体(流体和固体)的运动方程均可以用连续方程和动量方程表示为式(2)、式(3)：

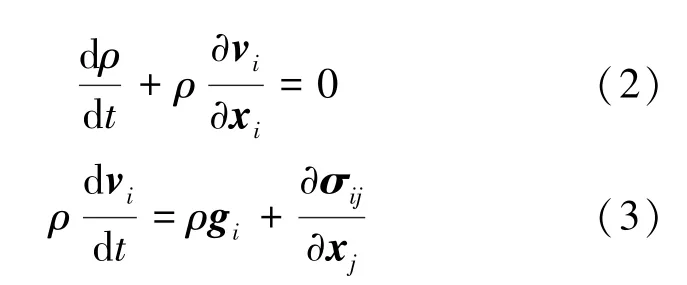
其中t 是时间，ρ 是密度， vi是速度向量， xi是位置向量，gi是重力向量，σij是应力张量。

采用光滑粒子流体力学方程时，根据定义恰当的核函数的密度分布，将连续体划分为若干质量为m 的准实体粒子，这时除在以粒子本身为圆心的沿半径2h(h 为用来刻画核函数尺度域的“光滑长度”)分布的圆周上的密度不为零外，其余各处均为零，据此可进行数值计算的离散[8]。

根据连续方程(2)，一般粒子α(流体或固体)的密度物质导数可以通过光滑粒子流体力学进行内插获得式(4)：

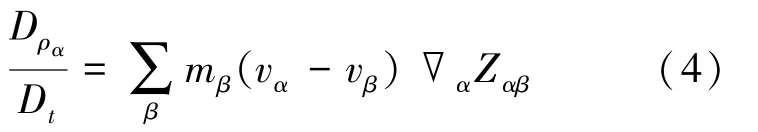
式中，对粒子α 尺度域内的周围所有粒子β求和，使用速度差分(vα- vβ)散度的近似是为保证常数速度场的密度物质导数为零；▽αZαβ是核函数在处的梯度。 其3 次样条曲线为式(5)：

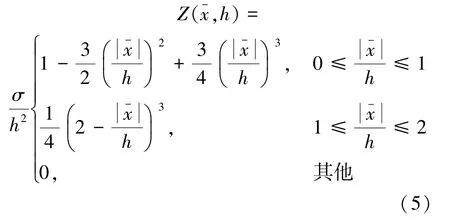
其中σ 是正交标准化常数，对于一般流体粒子α，动量方程(3)的光滑粒子流体力学方程可以写作式(6)：

人都聚集到了北坝两座山包间谷口处。迟恒惊慌失措赶到，不知道自己能做什么。狂泼的雨如同充满仇恨的怨妇，歇斯底里要用她的泪与呜咽去吞噬所有。他看见有人在架水泵、挖放泵的水洼，有人向坝堤外侧铺又长又宽的塑料布以作临时水渠，避免泄水冲涮砂质堤坝，迟恒赶紧过去帮着铺。很快，四台水泵开始抽吸库面积水往外吐。他从坝坡爬上来，水如蛇一样阴冷地已绕上脚根，不远处，魏昌龙蹲在坝旁一动不动死死盯着边线水位。迟恒刚想过去，突然想到极度紧张的人，很容易暴躁失控。

3.1.2 模拟结构的FEM 方程

利用虚功原理建立的非线性动力学有限元控制方程为式(7)：

式中，M 为质量矩阵，见式(8)；K 为总体刚度矩阵，见式(9)；Fext为外力矢量，见式(10)；fc为接触力。

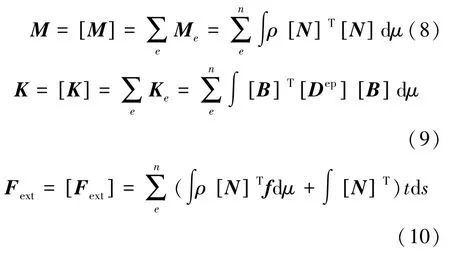
式中，f 为单位质量体力矢量，t 为面力矢量。

3.1.3 SPH-FEM 交界面接触处理

流体和结构分别采用了基于拉格朗日描述的SPH 方法和FEM 方法求解，因此可方便地通过接触算法处理流体与固体的交界面。 将SPH 粒子视为从节点，对应的结构面视为主面，在两者间建立基于罚函数方法的通用接触算法。 其原理是在每一时间步首先搜寻各从点是否穿透其靶点，没有穿透者不作任何处理；如果穿透，则在该从点和其靶点之间引入1 个较大的法向接触力，法向接触力正比于从点相对于其靶点的穿透量和表征接触碰撞界面刚度的罚因子，从而使穿透部分自动回到平衡位置。 在物理上相当于在从点与靶点之间放置一法向弹簧，以限制两者之间的穿透。

3.2 建模过程

用Radioss 有限元软件建立了洗衣装置洗涤过程的仿真模型，见图3。 模型中柔性袋内内容物会发生大变形，因此将其离散为SPH 粒子，其余部分离散为有限单元。 为简化计算，柔性袋内内容物不额外区分衣物和水，而是根据总体积离散为均匀密度的SPH 粒子。 SPH 粒子总体积为柔性袋容量的50%，等效为含水率300%的1 kg棉质衣物，由于微重力下衣物会悬浮于包内，故将粒子分布于柔性袋中央位置，粒子间隙为4 mm，粒子总数为11.9667 万。 洗衣装置结构尺寸如表1所示，柔性袋与凸包都为薄壁件，离散为壳单元，单元尺寸为4 mm 左右。 因凸包变形小且不受关注，为减少计算量，用RB2 单元将其刚化。 凸包与柔性袋单侧过盈量为5 mm。 模型中SPH 粒子分别与PP 框架、硅橡胶片建立接触连接，PP 框架单元与硅橡胶单元通过共节点连接，硅橡胶片分别与前凸包、后凸包建立接触连接。 仿真模型中各材料属性如表2 所示。

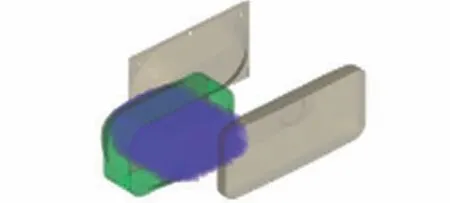
图3 仿真模型图Fig.3 Simulation model

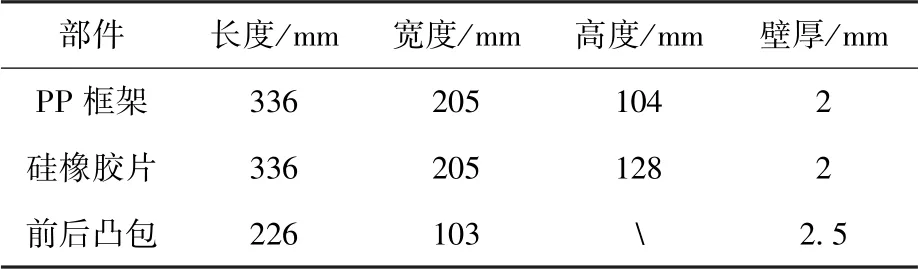
表1 洗衣装置结构尺寸Table 1 Dimensions of the washing device

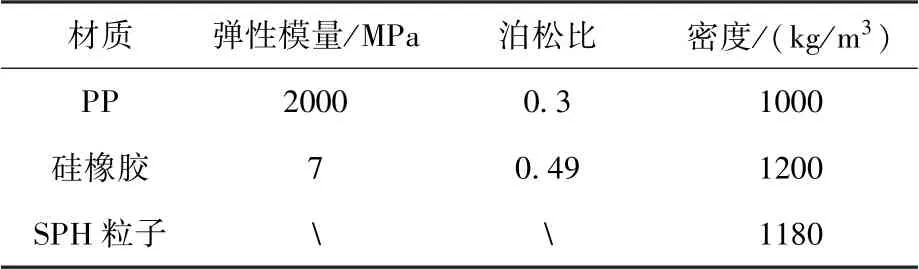
表2 仿真模型材料属性Table 2 Material features of the simulation model

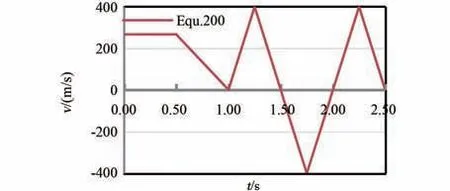
图4 洗涤包速度控制图Equ.200Fig.4 The controlled velocity figure Equ.200 of washing bag

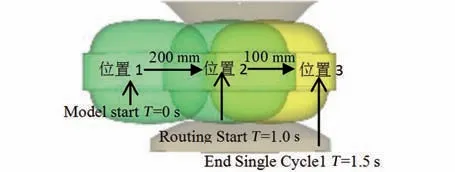
图5 洗涤包运动轨迹Fig.5 Movement locus of the washing bag

3.3 仿真结果

基于上文仿真模型可获取SPH 粒子和洗衣装置接触力以及粒子速度云图，其中粒子接触力可作为洗衣过程中机械力评价指标，粒子速度可作为洗衣过程中衣物翻滚评价指标。 图6 为仿真过程中， SPH 粒子与柔性袋PP 框架间、SPH 粒子与柔性袋橡胶片间、柔性袋橡胶片与凸包间的法向接触力合力随时间变化曲线图。 可以看出，代表衣物的SPH 粒子与柔性袋PP 框架间，不发生撞击时，作用力为0；发生撞击时会产生峰值应力，其中在第2 和第3 个单向行程中，各有一次撞击，分别产生130 N 与156 N 的峰值应力。 代表衣物的SPH 粒子与橡胶片间的作用力，在衣物撞击PP 框架前，就已开始增大，并在撞击时达到峰值49.2 N 与89.1 N。 这表明撞击前SPH 粒子在一端聚集，聚集的SPH 粒子受到凸包的挤压，使得接触力开始增大，撞击PP 框架后粒子散开来，在凸包挤压作用与粒子撞击橡胶片的共同作用下，使得接触力达到峰值。 凸包对橡胶片的挤压力，稳定在17.6 N，在SPH 粒子与PP 框架撞击前后时，因粒子聚集，挤压力增大。

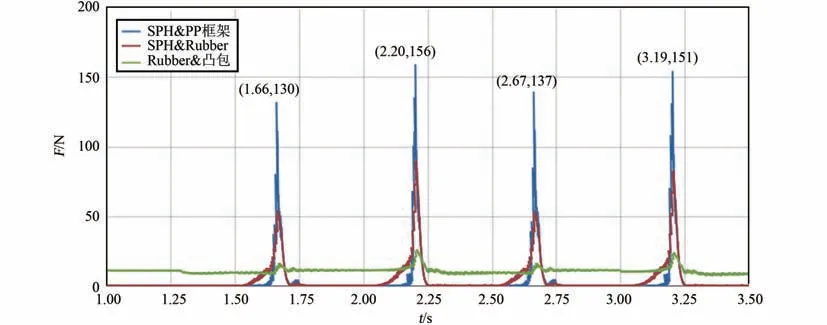
图6 接触力与时间曲线图Fig.6 The normal contact force over time

图7 为SPH 粒子撞击柔性袋时模型的x 方向速度云图，图7(a)为t ＝1.66 s 时刻，即第一次撞击时的情形。 此时柔性袋速度为沿x 负方向，靠右端与柔性袋接触的粒子，速度已变为沿x 正向，靠左端大部分粒子仍具有沿x 正向的速度。粒子的这一速度变化过程可代表此时衣物有1 个翻转运动过程。 类似图7(b)为t＝2.2 s 时刻第2次撞击时的情形，此时也代表衣物有一个翻转运动过程。

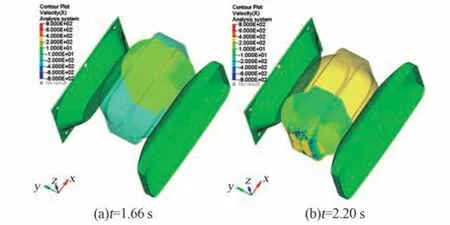
图7 SPH 粒子撞击PP 框架时速度云图Fig.7 The velocity contour plot when SPH particles hit PP Frame

根据式(1)可计算初版装置洗净参数I1＝f1·n1·m1·j1＝94.2，其中机械力f1＝(130+156+49.2+89.1)/2 ＝212.15 N，n1＝2/3，m1＝2/3，j1＝1。同样可计算滚筒洗衣机洗净参数：以内桶直径D＝500 mm 滚筒洗衣机为参考，2 kg 重物提升至桶内最高点，然后自由落体，取冲击时间为15 ms，由动量定理mv＝ft 得出冲击力为417 N，即有fbase＝417 N，nbase＝1，mbase＝1，jbase＝1，得出Ibase＝417。由于初版装置洗净参数I1＜Ibase，因此需对当前系统进行优化，提高装置的洗净能力。

4 仿真优化

为提升洗涤装置的洗净能力，本文从柔性包速度和凸包凸台结构2 方面进行优化。

4.1 速度参数优化

建立了速度优化模型，与原模型相比，仅PP框架的x 方向速度约束更改为图8(0.25～1.25 s洗涤包的平均速度为400 mm/s，故下文均以图Equ.400 表示)。 图9～11 分别为优化前后的结果对比图，且将优化后结果的时间轴数值放大了1倍。 对比图9 中SPH 粒子与PP 框架接触力可知，第1 次撞击的峰值应力由130 N 提升为379 N，第2 次撞击峰值应力由156 N 提升为520 N，撞击力度提升了约3 倍。 对比图10 中SPH 粒子与橡胶片间的接触力，可知峰值接触力分别为160 N 与300 N。 结合图11 中凸包与橡胶片间的接触力，可知凸包过盈挤压时的稳定接触力没变，此时凸包对衣物挤压力的增大主要来自于撞击时速度的提升。 综合而言，同等情况下，速度提升1 倍，衣物撞击PP 框架时，整个柔性袋传递给衣物的峰值力提升了约3 倍，撞击频率与翻转频率没变。 据分析结果有f ＝(379+520+160+300)/2 ＝679.5，n ＝2/3，m＝2/3，J ＝1，计算得I2＝302。 比较得I1＜I2＜Ibase，即速度优化后，洗净能力有提升，但仍没达到当前滚筒洗衣机标准。

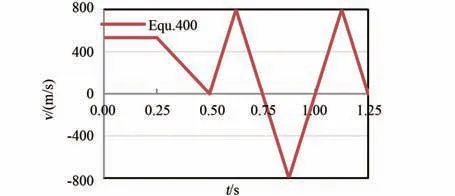
图8 洗涤包速度控制图Equ.400Fig.8 The controlled velocity figure Equ.400 of washing bag

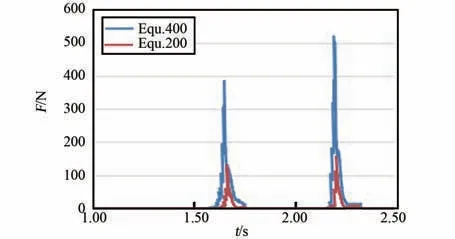
图9 SPH 粒子与PP 框架接触力Fig.9 The contact force over time between SPH partials and PP frame

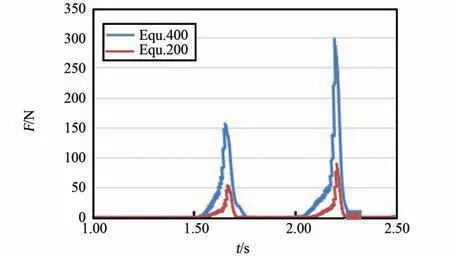
图10 SPH 粒子与橡胶片接触力Fig.10 The contact force over time between SPH partials and rubber sheet

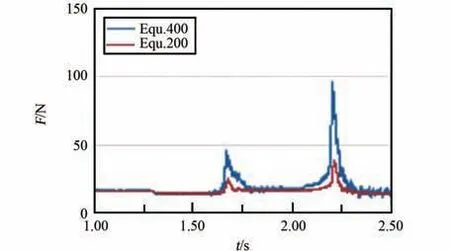
图11 凸包与橡胶片接触力Fig.11 The contact force over time between bumps and rubber sheet

4.2 凸包凸台结构优化

图12 凸包凸台结构优化模型Fig.12 The simulation model with bumps structure optimized

在4.1 基础上继续优化，将原凸包优化为图12中的结构，即在原凸包上增加高为30 mm 的凸台。前后凸包上的凸台交叉分布，分别为1 个和2 个。图13～15 为更改前无凸台结构与更改后有凸台结构的仿真结果对比图。 图13 显示有凸台时，在第2个单向行程中，SPH 粒子与橡胶片有2 次(t ＝0.81 s、t ＝0.86 s)连续撞击，分别产生峰值162 N 与78.1 N 的峰值力；第3 个单向行程2 次连续撞击(t＝1.07 s、t＝1.11 s)分别产生361 N与97.7 N 的峰值力。 对比无凸台结构仿真结果，撞击产生的峰值力下降，撞击频率提升1 倍。 图14 为SPH 粒子与PP 框架间的接触力，结果显示，有凸台时，每次撞击前后，高挤压力作用的时间会明显增长。 图15解释了橡胶片与凸包接触力随时间的变化关系，因前后凸包上凸台间隔作用，橡胶片受到约80 N 的挤压力且时间较长，一旦SPH 粒子聚集，橡胶片受到的挤压力就会传递给SPH 粒子，且将聚集的SPH 粒子挤散，这很好地解释了橡胶片与SPH 粒子间高挤压力作用时间长的原因。 图16 显示了SPH 粒子撞击PP 框架时模型的速度云图，查看图中柔性袋与粒子的变化形态，以及粒子速度分布，可知有凸台后，衣物易被展开，翻转效率提升0.5倍。 综合而言，增加凸台后，衣物撞击PP 框架时，整个柔性袋给衣物的峰值力下降约1 倍，撞击频率提升1 倍，凸台易于将团起的衣物展开，衣物翻转效率提升0.5 倍。 据分析结果有f ＝(162+78.1+361+97.7+80×4)/4 ＝254.7，n ＝4/3，m ＝4/3，J ＝3/2，计算得I3＝679.2。 比较得I3＞Ibase＞I2，即同时进行速度优化与结构优化后，洗净达到了当前滚筒洗衣机标准。

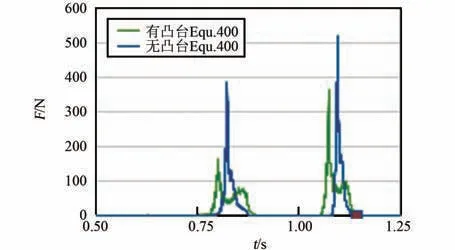
图13 SPH 粒子与橡胶片接触力Fig.13 The contact force over time between SPHpartials and rubber sheet

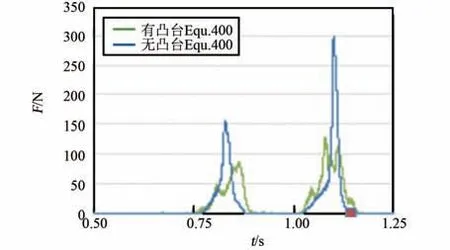
图14 SPH 粒子与PP 框架接触力Fig.14 The contact force over time between SPH partials and PP frame

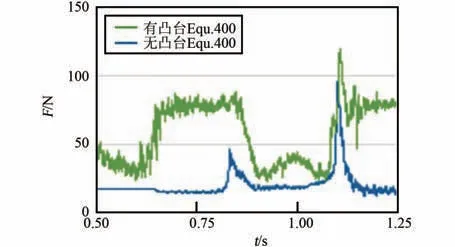
图15 橡胶片与凸包接触力Fig.15 The contact force over time between rubber sheet and bumps

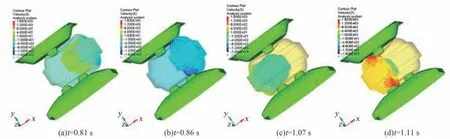
图16 SPH 粒子撞击PP 框架时速度云图Fig.16 The velocity contour plot when SPH particles hit PP Frame

4.3 情形对比

柔性袋内内容物容量不同时，洗净能力会有差异。 因此建立了内容物占柔性袋96%容量时的模型如图17，以衡量接近满负载状况下，所设计洗衣装置的洗净能力。 图18～20 为同等条件下，50%与96%内容物仿真结果对比图。 图18 显示，内容物增加到96%后，由于柔性袋内空隙小，撞击次数增加，每个单向行程中至少会发生1 次SPH粒子与PP 框架的撞击，撞击峰值力度分别为231.9 N、473.7 N、217.8 N 与286.1 N。 图19～20显示，内容物增加到96%后，SPH 粒子一直处于聚集状态，没有足够的空间展开。 因此，凸包凸台会持续挤压橡胶片，进而挤压SPH 粒子，每个单向历程中会持续受到与峰值力100 N 相当的挤压力。结合图21 第1 个单向行程形态图，可知撞击后粒子速度缓慢变为0，而不是迅速反向，此时翻转效率极低。 综合而言，与50%内容物相比，当柔性袋内有96%内容物时，衣物撞击PP 框架时，袋内衣物受到的峰值力增大1 倍，撞击频率提升0.3 倍，翻转效率降低0.5 倍。 计算得f ＝(231.9+473.7+217.8+286.1+100×4)/4 ＝402.4，n ＝4/3，m ＝4/3，J＝1/2，I4＝357.7。 I4＝0.86Ibase，表明洗净没达到当前滚筒洗衣机标准，需增加约1/5 的洗涤时长。

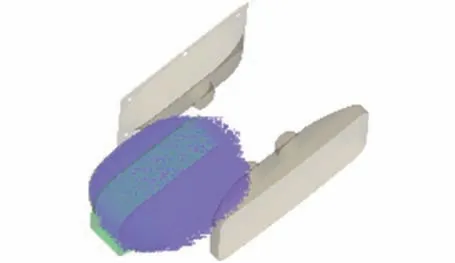
图17 优化后96%内容物模型Fig.17 The simulation model with 96%volume occupied

图18 SPH 粒子与PP 框架触力Fig.18 The contact force over time between SPH partials and PP frame

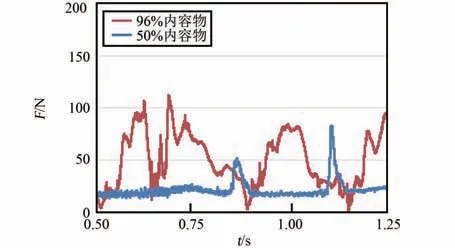
图19 SPH 粒子与橡胶片接触力Fig.19 The contact force over time between SPH partials and rubber sheet

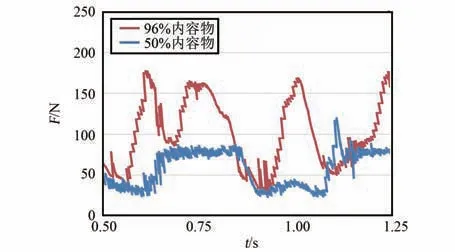
图20 橡胶片与凸包接触力Fig.20 The contact force over time between rubber sheet and bumps

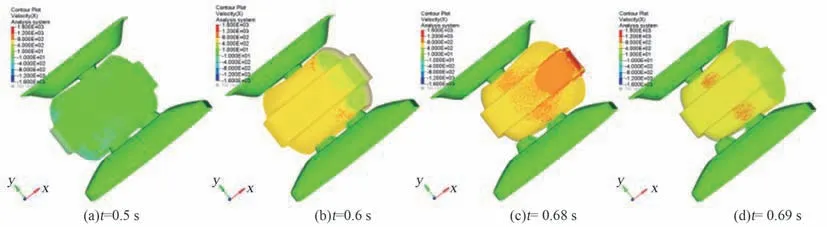
图21 96%内容物模型第1 个单向历程中速度云图Fig.21 The velocity contour plot of 96%volume occupied model during the first single routing

5 结论

1)建立了基于光滑粒子动力学法(SPH)与有限元法(FEM)耦合的流固耦合模型，获取了SPH 粒子和洗衣装置接触力以及粒子速度云图，粒子接触力作为洗衣过程中机械力评价指标，粒子速度作为洗衣过程中衣物翻滚评价指标。

2)柔性袋速度提升和凸包增加凸台结构均能增大洗涤过程机械力。 柔性袋速度提升1 倍，同时挤压凸包增加凸台结构，在50%负载工况下装置能达到当前滚筒洗衣机相近的洗净度。

3)洗涤衣物量影响洗衣装置洗净能力，可通过增加洗涤时长相应提升洗净能力。

参考文献(References)

[1]强洪夫.光滑粒子流体动力学新方法及应用[M].北京：科学出版社，2017：20-49.Qiang H F.New Method and Application of Smoothed Particle Hydro-dynamics[M].Beijing： Science Press， 2017： 20-49.(in Chinese)

[2]王勖成.有限单元法[M].北京：清华大学出版社，2003：468-520.Wang X C.Finite Element Method[M].Beijing： Tshinghua University Press， 2003： 468-520.(in Chinese)

[3]Attaway S W，Heinstein W M，Mello F J，et al.Coupling of smooth particle hydro-dynamics with PRONTO[C]/ /1993 ASME Winter Annual Meeting，New Orleans，1993.

[4]Attaway S W，Heinstein W M，Mello F J.Coupling of smooth particle hydrodynamics with finite element method [J].Nuclear Engineering and Design，1994，150：199-205.

[5]Sonia F，Javier B，Antonio H.Continuous blending of SPH with finite elements[J].Computer ＆ Structures，2005，83：1448-1458.

[6]马利，陶伟明，郭乙木， 等.SPH 耦合有限元方法的水射流弹塑性碰撞模拟[J].浙江大学学报，2008，42(2)：259-263.Ma L， Tao W M， Guo Y M，et al.Elastic/plastic impact simulation of water jet using smoothed particle hydrodynamics and finite element method[J].Journal of Zhejiang University，2008， 42(2)： 259-263.(in Chinese)

[7]肖毅华，韩旭，胡德安.流体与结构相互作用问题的FESPH 耦合模拟[J].应用力学学报，2011，28(1)：13-18.Xiao Y H， Han X， Hu D A.FE-SPH coupling simulation of fluid-structure interaction problems[J].Chinese Journal of Applied Mechanics， 2011， 28(1)： 13-18.(in Chinese)

[8]孙芳锦，张大明.基于光滑粒子流体动力学的流固耦合问题研究[J].地震工程与工程振动， 2013， 33(6)： 222-227.Sun F J， Zhang D M.Study on fluid-structure interaction based on smoothed particle hydro-dynamics[J].Journal of Earthquake Engineering and Engineering Vibration，2013，33(6)：222-227.(in Chinese)