局部SRC二次转换结构受力性能研究

邓智元，陈思坚

(1.福建工程学院土木工程学院，福建 福州 350118；2.福建省土木工程新技术与信息化重点实验室，福建 福州 350118)

梁式转换层结构因其受力性能好、传力途径明确、施工简单以及结构计算方便等众多优点在国内外高层建筑中被广为采用[1]。常见的梁式转换层结构多采用一次转换，但现实工程中转换梁上部的墙体多为L 型的墙肢，无法全部落在框支主梁上，需要进行二次转换[2]。由于二次转换结构体系传力不直接，易对转换主梁产生较大的扭矩和剪力，加上次梁进一步减小了转换主梁的剪跨比，使转换主梁很容易发生剪切破坏。

我国现行《高层建筑混凝土结构技术规程》[3]第10.2.16 条规定：B级高度部分框支剪力墙高层建筑的结构转换层，不宜采用框支主、次梁方案。虽然规范对A级高度部分框支剪力墙结构无此限制，但也没有明确规定对此类结构应如何设计，因此对转换层的理论研究很有现实意义。现有的转换层结构研究主要集中在一次转换上，二次转换结构体系的研究仅限于工程特例的具体分析。例如：雷静[4]、马斐[5]、R.S.Londhe[6]、R.K.L.Su[7]以及关立军[8]等人分别对广州、佛山、大连带主次梁转换层的复杂高层建筑结构进行了分析，针对具体建筑给出了设计建议。

本文针对二次转换结构产生的不利因素，提出在主次梁交接处至支座处局部加设型钢，形成局部型钢混凝土(steel reinforced concrete,SRC)二次转换结构[9]，利用有限元分析法分析RC二次转换结构和局部SRC二次转换结构在不同剪跨比下表现出来的抗剪、抗扭、应力分布等性能，为局部SRC二次转换结构的适用范围提供一个合理的建议值。

1 转换层结构整体模型研究

1.1 模型概况

为确保有限元模型的正确性，以文献[10]的转换结构拟静力加载试验为参考。考虑转换梁和上部剪力墙协同工作[2]，墙体取3层，混凝土均为C30，型钢采用Q-345B，钢筋采用HRB400级。构件尺寸信息如图1所示。

图1 构件尺寸及配筋图(单位：mm)Fig.1 Component size and reinforcement diagram(unit: mm)

1.2 材料本构及网格划分

混凝土采用塑性损伤模型本构关系模型(concrete damaged plasticity)[4]，钢材均采用双折线强化本构关系模型[11]。

为了更真实地模拟实际结构受力状态，除了钢筋采用桁架单元模拟，其余构件均用实体单元，选择精度较高的结构化技术分割方式进行网络划分，钢筋单元每8 cm划分为一个网格尺寸，混凝土每4 cm进行一次网格分割。钢筋与混凝土和型钢与混凝土接触面均采用有限元通用软件ABAQUS自带的Embed关系模型，柱下端边界条件采用固结方式(U1=U2=U3=0)，有限元模型如图2所示。

图2 混凝土、钢筋有限元模型Fig.2 Finite element models of concrete and reinforcement framework with steel bars

1.3 模型验证

有限元计算结果与试验结果的滞回曲线以及骨架曲线对比如图3-4所示。由图可见，有限元模拟和试验结果拟合较好，因此该建模有效。

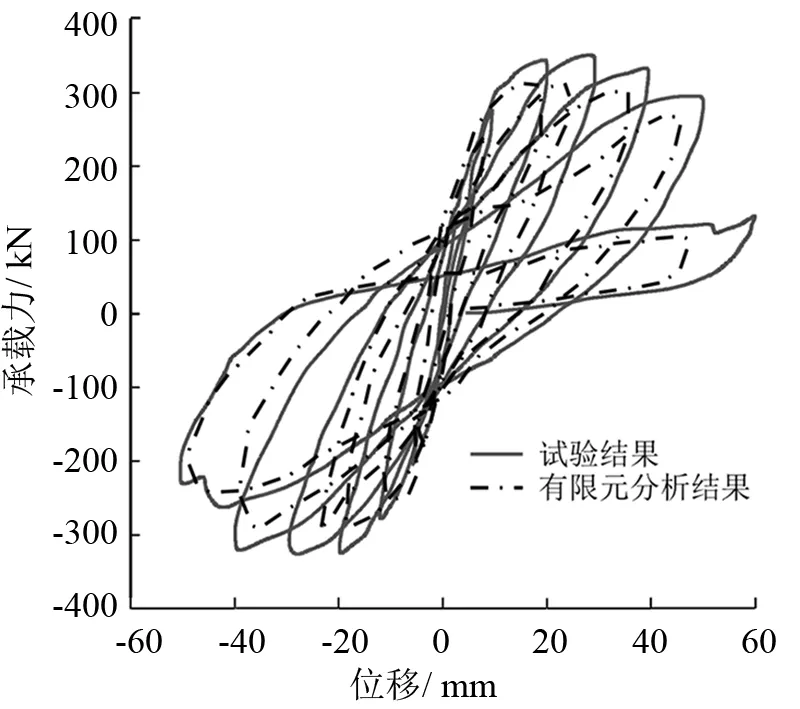
图3 滞回曲线对比Fig.3 Hysteresis loop chart

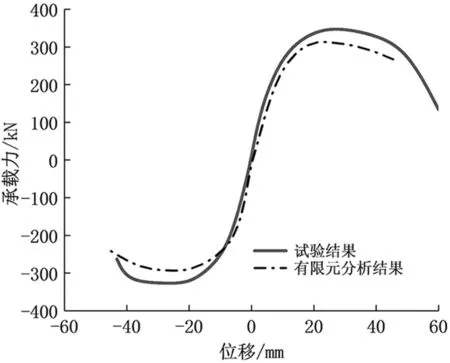
图4 骨架曲线对比Fig.4 Comparison of skeleton curves

1.4 计算结果分析

为进一步模拟非整体模型的工况和不同楼层共同工作的工况，计算时对上部墙体层数n从0到5依次加载模拟，其中n= 0表示不考虑转换梁和墙体的协同效应。各种工况下，n对转换梁的轴力(N)、剪力(V)、弯矩(M)影响如图5(a)-(c)所示。

从图5(a)-(c)中可以直观看出：(1)n= 0时，不考虑转换梁和上部墙体协同效应，转换梁的弯矩、剪力、轴力远大于考虑协同效应，在数值上比大了近一倍；(2)n< 3时，考虑转换梁和上部墙体协同效应，转换梁内力相差较大，均超过10%；(3)n≥ 3时，考虑转换梁和上部墙体协同效应，其内力相差较小，弯矩最大相差仅0.36%，剪力最大相差仅0.96%，而轴力最大相差2.04%；最大内力差值均小于5%，并且4 ≤n≤ 6时，内力均趋于稳定。因此，取n= 3既可满足其精度要求又减小了计算量、提高了效率。

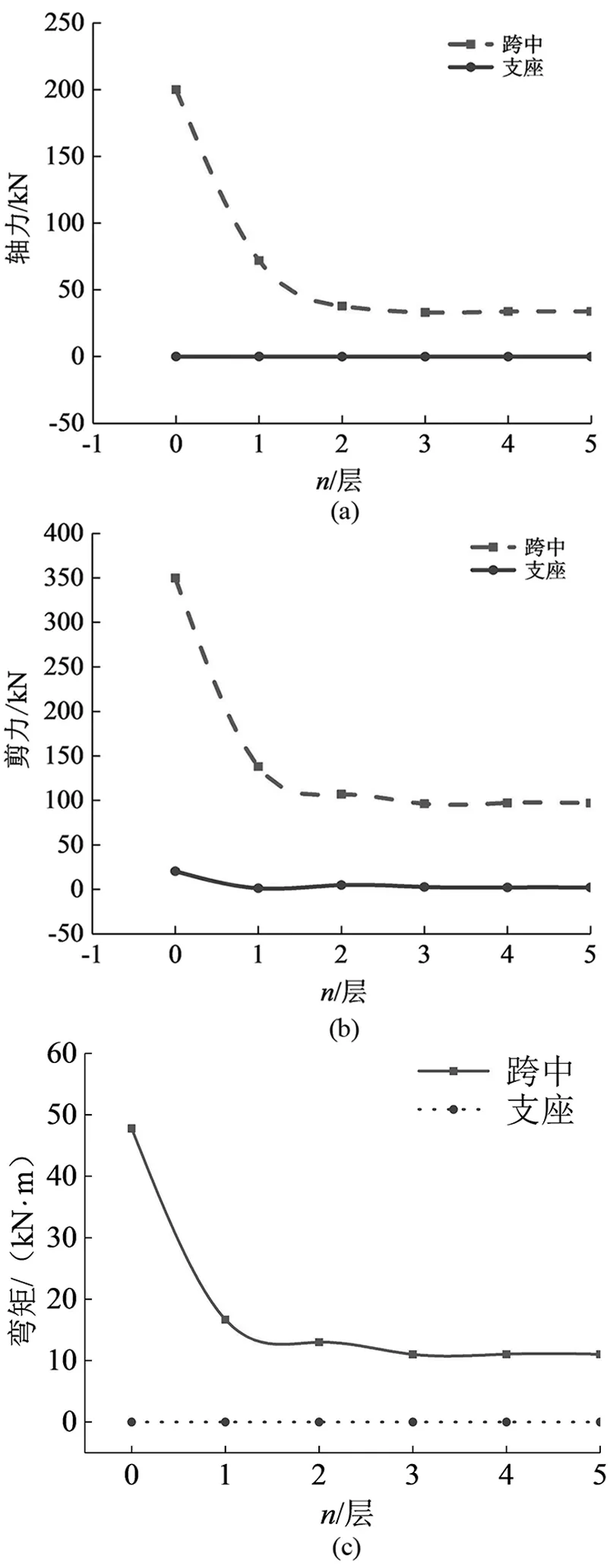
图5 转换梁内力随楼层的变化图Fig.5 Diagram of the internal force of the transfer beam changing with the floor number

2 局部SRC转换梁力学性能对比分析

2.1 有限元模型建立

对RC二次转换结构和局部SRC二次转换结构(结构构造如图6所示)分别进行有限元受力分析，对比两者转换主梁的抗扭和抗剪性能。为了建模方便，在进行二次转换结构建模分析时候，用扭矩(T)和集中力(F)代替次梁及其上部剪力墙所产生的效应，计算时候取3层墙体，型钢尺寸为100 mm × 100 mm × 8 mm× 10 mm，有限元模型如图7所示,建模方式与前小节相同，不再赘述。

图6 局部SRC转换结构构造图Fig.6 Construction of local SRC transfer structure

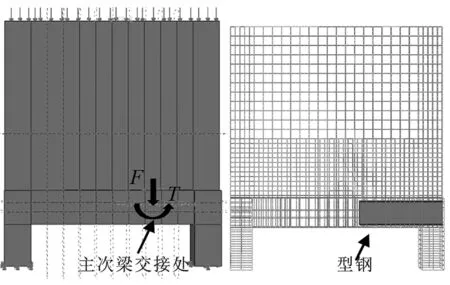
图7 混凝土及钢筋有限元模型Fig.7 Finite element models of concrete and reinforcement framework with steel bars

2.2 内力对比分析

根据有限元计算结果，分别提取出局部SRC转换梁、SRC转换梁、RC转换梁的梁左、梁右、主次梁交接处以及跨中截面的内力，并分析对比其抗剪和抗扭性能，具体结果见表1-3。

由表1-3可以看出：(1)和RC转换梁相比，局部SRC转换梁在主次梁交接处的剪力值减小11.51%，扭矩值减小10.90%，明显提高了转换梁的抗剪和抗扭性能，缓解了二次转换产生的扭转效应；(2)和SRC转换梁相比，局部SRC的抗剪能力达到SRC转换梁的75.46%，抗扭能力达到72.60%，而用钢量仅占SRC转换梁的33.33%，因此采用局部SRC转换梁总体上更经济、合理。

表1 局部SRC转换梁内力

2.3 应力对比分析

根据有限元计算结果分别提取出转换梁上表面中轴线应力，见图8所示。

从图8可以看出，二次转换结构在主次梁交接处产生应力集中，其中，局部SRC转换梁在主次梁交接处应力值可减小约23.23%，与SRC转换梁相差不足5%。

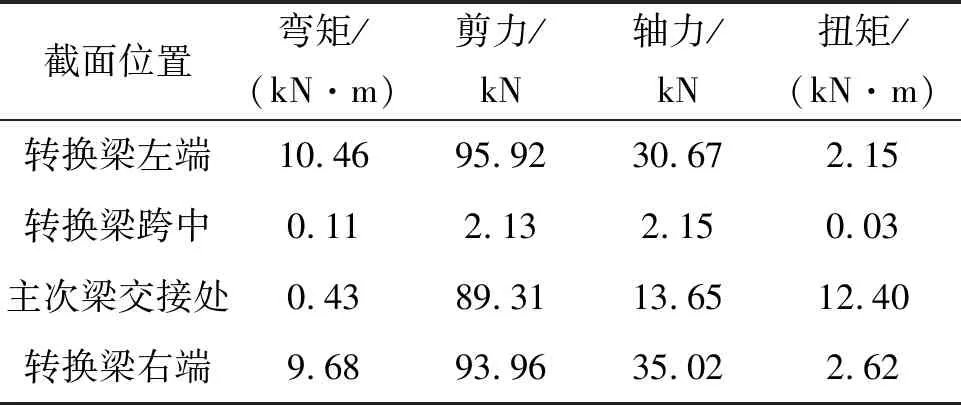
表2 SRC转换梁内力

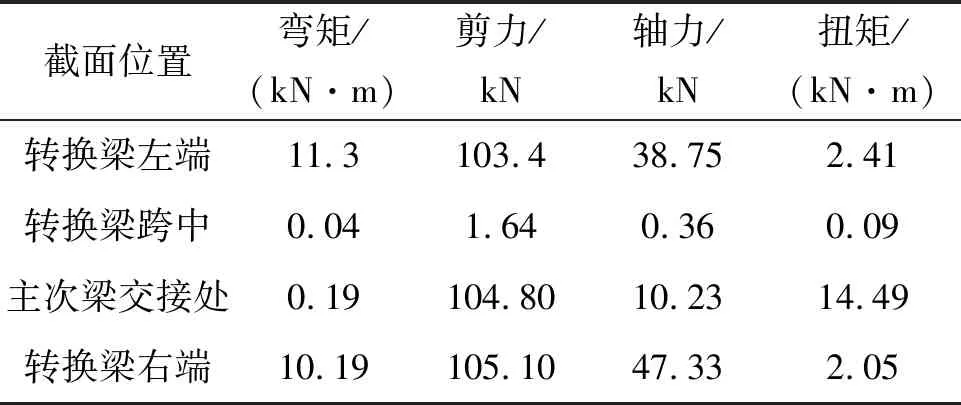
表3 RC转换梁内力

图8 不同形式转换梁其应力对比图Fig.8 Stress comparison of different types of transfer beams

3 剪跨比对局部SRC转换梁影响分析

从第2节得知，局部SRC转换结构不仅比SRC结构更节省钢材，也有效缓解了扭转效应和应力集中等二次转换带来的不利因素。为进一步了解剪跨比对局部SRC转换结构的抗剪和抗扭影响，确定局部SRC二次转换结构的适用范围，分别取净跨0.1l0、0.2l0、0.3l0、0.35l0、0.4l0、0.5l0,(l0为梁净跨)对应剪跨比λ：0.63、1.27、1.90、2.53、2.85、3.17进行有限元受力分析，结果见表4-5。

表4 转换主梁剪力值

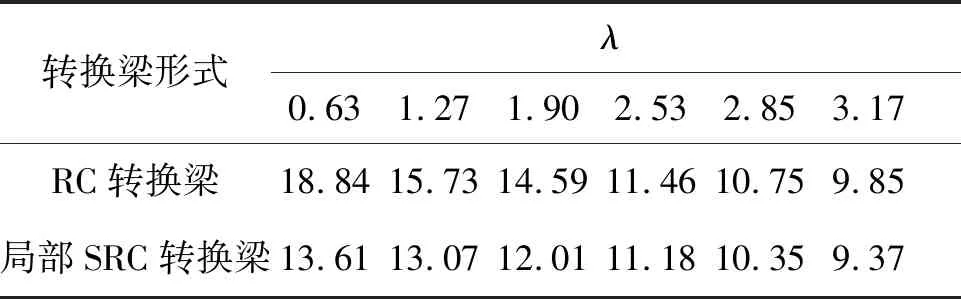
表5 转换主梁扭矩值

从表4-5可以得出:(1)当0.63 ≤λ≤ 1.90时，局部SRC转换梁剪力值最大减小28.87%，扭矩最大减小27.76%，(2)当λ> 1.90时，局部SRC转换梁剪力值最大仅减小7.91%，而扭矩值最大仅减小4.87%。综上，局部SRC转换梁提高了二次转换结构的抗剪和抗扭性能，减小了扭转效应，剪跨比处于0.63～1.90时，其抗剪和抗扭均能减小20%以上，当剪跨比大于1.90时，其剪力值和扭矩值最多减小不到8%，故建议此类局部SRC二次转换结构剪跨比适用范围在0.65～1.90。

4 结论

1)对带转换层结构进行有限元建模分析时，应考虑转换梁和上部墙体的协同效应，为减小与真实值之间的误差，上部层墙体结构取值不应小于3层。

2)同RC转换梁相比，局部SRC转换梁可大幅度降低主次梁交接处的应力集中和扭转效应；与SRC转换梁相比，局部SRC转换梁的剪力值和扭矩值可达到SRC转换梁的70%，但局部SRC转换梁用钢量仅占SRC转换梁的33.33%。综合考虑，采用局部SRC转换梁更为经济合理。

3)由于剪跨比不同，局部加钢的转换梁对扭转效应和应力集中的缓解情况不一，计算结果表明：当剪跨比介于0.65～1.90时，局部SRC二次转换结构的抗扭、抗剪效果最佳。