考虑路网拥堵状态的出行者主观路径选择模型
张卫华,颜 鹏,黄志鹏
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
0 引 言
出行者路径选择是交通领域研究的热点问题,其结论的科学性直接影响到交通配流模型的可靠性。早期学者对出行者路径选择问题的研究,通常假设出行者是完全理性的、具有完全的信息和相同喜好,采用效用理论建立出行路径选择模型。随着行为科学的发展和实践,已有研究者考虑了出行者的有限理性,D. KAHNEMAN等[1]在有限理性基础上提出了前景理论(prospect theory, PT),用价值函数替代效用函数;A. TVERSKY等[2]完善了PT,发展成为累积前景理论(cumulative prospect theory, CPT)。由于能够较为贴近实际描述出行者决策行为,PT和CPT被广泛应用于交通研究领域。徐红利等[3]、杨志勇等[4]、XU H L等[5]、李小静[6]及陈玲娟等[7]均以路径为直接研究对象,假设路径行程时间为连续的概率函数,出行者在完全理性或者不完全理性情况下对路径进行选择,从而建立相应的出行者路径选择模型。
传统的基于累积前景理论的出行者路径选择模型将路径作为研究对象来计算前景值,而在实际路网中,难以得到路径行程时间及概率分布,并且路径行程时间与路网交通负荷紧密相关,路径行程时间分布在不同的时段是有差异的,因此传统的基于累积前景理论的出行者路径选择模型不能体现路网的拥堵状态的变化对出行者路径选择的影响。笔者针对传统路径选择行为模型中未考虑路网拥堵状态这一影响因素的问题,从路段的角度研究不同路网拥堵状态下,路径行程时间的概率模型,通过累积前景理论对出行者选择行为进行分析,探索更加符合实际的出行者路径选择模型。
1 改进的基于CPT主观路径选择模型
1.1 基于CPT传统路径选择模型问题分析
根据累积前景理论,当出行者通过考虑自身可以获得的效用大小进行路径选择时,出行者进行路径选择的行为可分为3个阶段:
1)编辑阶段。出行者初步分析路径的信息,根据出行需要,将备选路径的出行效用编译为自身的收益或者损失。
2)估值阶段。根据编辑阶段的收益和损失值,确定主观概率和主观效用,从而获得路径的感知价值(即前景值)。
3)选择阶段。出行者在备选路径中选择感知价值最大的路径出行。
出行者在有限理性的情况下进行路径选择,是依靠其对路径的感知价值,而感知价值通过主观效用函数v(x)和主观概率函数π(P)获得。主观效用函数是出行者根据实际效用x形成的主观感知效用,体现了出行者对实际效用的主观判断程度;主观概率函数是出行者根据路径实际效用发生的概率P形成的主观概率,体现了实际效用的概率分布对感知价值的影响。
假设一次出行有f+g+1个到达时刻,其中晚于参考点到达时刻有f个,早于参考点到达时刻有g个,通过主观效用函数和主观概率函数可计算路径l前景值:
(1)
式中:Ph为到达时刻为第h个时刻的概率;π-(Ph)为出行者感受损失时的主观概率;π+(Ph)为出行者感受收益时的主观概率。
这种以前景值为判断指标的传统CPT路径选择模型,一般是假设路径行程时间分布函数已知或直接给定行程时间所对应的概率。而道路交通网络系统受到外界很多因素的影响,是一个复杂的系统,表现出一定的时空动态特性。不同的路网拥堵状态下,路径的行程时间分布不尽相同,出行者选择路径的结果不同,表现为不同的出发时段路段行程时间不同,如高峰时段出行,出行者会更加有意识地避开拥堵路段,以保证能在预期时间内抵达目的地。
因此,对于同一条路径,在不同的拥堵状态下,出行者对其的感知价值是有差异的。采用固定函数表示路径行程时间不能体现路网拥堵状态的变化对出行者决策行为的影响。对出行者路径选择行为建模时,应当考虑路网拥堵状态对出行者的影响。
1.2 改进模型
出行者在进行不确定性决策时,通过对已知信息的处理,形成主观判断,即路径某一效用实际发生的概率转变为出行者主观概率。在不同的出行时段,实际路网中各路径的拥堵状态不同,出行者所获得的路径信息是不同的,即同一路径的行程时间概率函数是不同的,因此出行者选取的参考点和路径前景值也不尽相同。如图1,当考虑不同交通拥堵状态时,采用传统模型对路径前景值求解,同一参考点下前景值存在唯一解;而考虑路径拥堵状态时,由于行程时间函数不同,同一参考点下路径前景值不同。
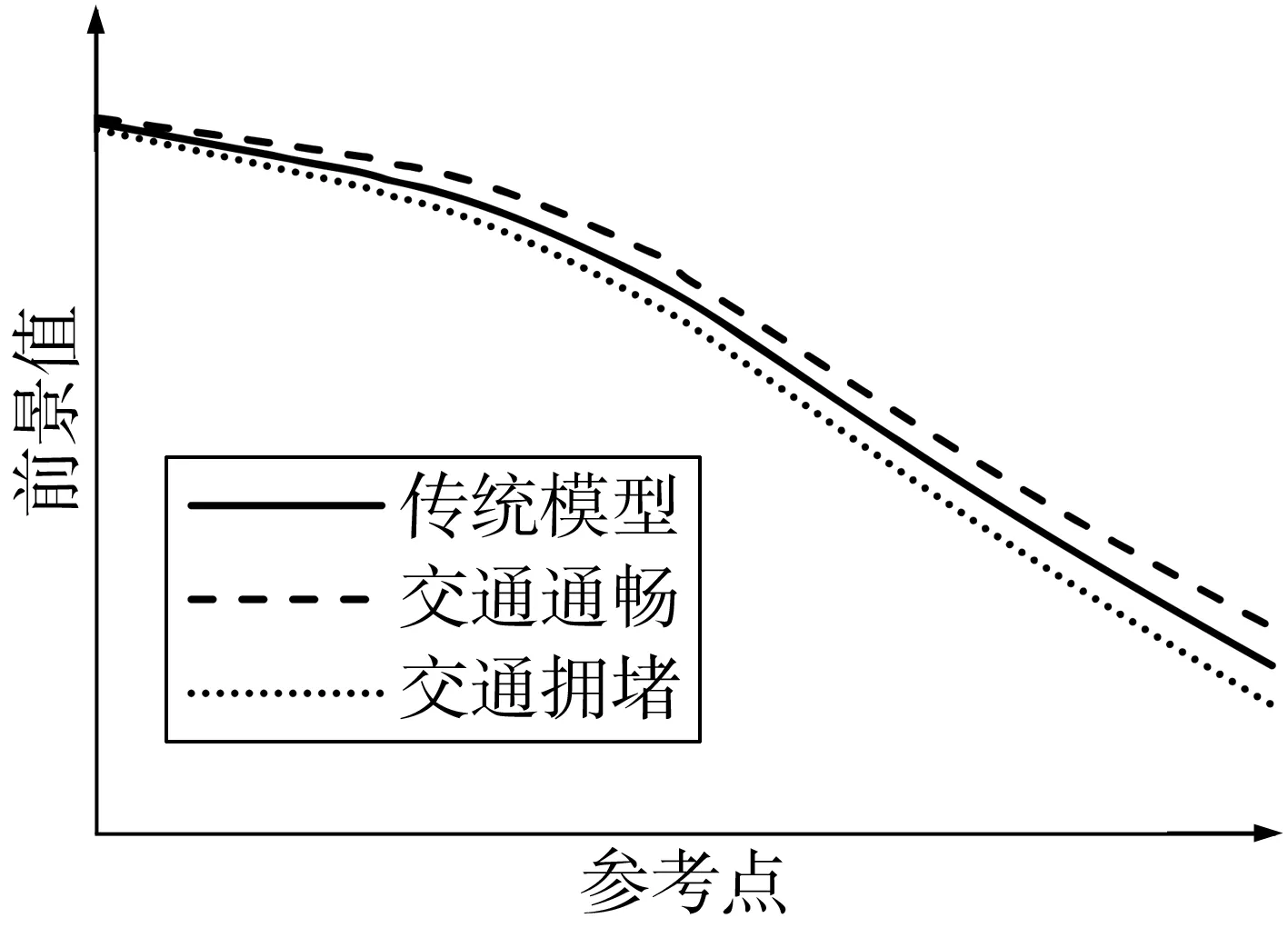
图1 不同交通状态的前景值-参考点曲线Fig. 1 The relationship curves between reference points and prospect value of different traffic states
假定出行者一次出行可以获得一定的效用,其完成该次出行能够获得的最大收益是xmax,而选择某一路径l的出行费用是c,则出行者选择路径lj可以获得的效用是[8]:
xj=xmax-c
(2)
出行者的一次出行中,行程花费时间为T,必须在预期时间T0之内到达目的地,否则将会产生如下损失[9]:
早于预期时间到达会产生早到损失费用c1:
c1=θ1(T0-T)
(3)
晚于预期时间到达会产生迟到损失费用c2:
c2=θ2(T-T0)
(4)
1)若出行者完成一次出行的通行时间费用为θ3·T,则总损失费用为:
(5)
式中:θ1、θ2、θ3分别为早到、迟到和行程过程中的单位时间价值系数,根据K. A. SMALL[10]的研究成果,有θ2>θ3>θ1。
2)若出行者对于一次出行能够获得的效用心理参考点为x0,则主观感知效用可以分为收益部分(xj≥x0)和损失部分(xj (6) 效用敏感系数0<α,β≤1,反映出行者对实际效用变化的感知敏感程度;损失规避系数λ>1,反映出行者面对相同效用的收益与损失之间的感知程度差异。 0≤h (7) 1-f≤h≤0 (8) (9) 式中:γ为概率权重系数,根据D. KAHNEMAN[1]对参数γ的标定,获得收益时γ=0.61,发生损失时γ=0.69。 (10) 路径是由路段组成的,组成路径的各路段行程时间相加即可得到该路径行程时间。不同的路网拥堵状态下路段行程时间分布不同,因此可从路段角度研究路径行程时间概率,得到基于路段单元的路径行程时间概率。 路段行程时间是连续变量,难以直接推导路径行程时间函数,考虑到出行者对时间长短的感知程度是有限的,可把路段行程时间离散化,将路段行程时间用离散分布函数表示,以得到基于路段单元的路径行程时间概率函数。 设:ai为路网中的路段(i为路网中路段编号),A为路网中路段的集合,ai∈A,qi/Ci为路段ai的饱和度,ti为是路段ai的行程时间,ti=ki·Δt(ki为整数,取值为1、2、3、…,Δt为时间单元)。 定义:Δt为出行者认为路段行程时间等于ti或ti-ε对自身的效用相等时,ε的最大值。由于出行者对时间的敏感程度是有限的,取ε≥1/50T,即Δt≤1/50T。 假设路段ai饱和度为qi/Ci时,其行程时间ti的概率密度函数为f(ti,qi,Ci),行程时间概率函数为F(ti,qi,Ci),也就是路段ai行程时间小于ti的概率为F(ti,qi,Ci),即图2中累积概率函数。将路段ai行程时间ti作离散化处理:由Δt定义行程时间取值为区间((ki-1)·Δt,ki·Δt]内任意一点等同于行程时间为ki·Δt,则可以认为路段ai的行程时间小于ki·Δt的概率等于路段ai的行程时间小于区间((ki-1)·Δt,ki·Δt]内任意一点的概率,即图2中离散化函数,则,路段ai的行程时间为ki·Δt的概率为: (11) 图2 概率-行程时间曲线Fig. 2 The curve of probability and travel time 将路径看作是路段的组合,若路径lj由m条路段组成,按照走行顺序分别是aj1,…,aji,…,ajm,记为路径lj(aj1,…,aji,…,ajm)。 由于各路段行程时间ti是离散量,所以路径lj的行程时间Tj也是离散量,记: (12) 根据式(11)、式(12),即可在已知路段饱和度条件下,求得路径lj任意行程时间取值对应区间的概率,即路径行程时间概率函数。 根据基于路段单元的路程概率-行程时间函数建立出行路径选择模型,考虑到路网拥堵状态对行程时间函数的影响,区别于传统路径选择模型直接给定路径行程时间分布,因此求解时应当先对路径行程时间函数进行预处理,得到各种路网状态下的路段行程时间分布函数,从而计算各条路径行程时间函数,以此为基础计算各条路径前景值。具体步骤如下: Step0:路段数据初始化。将路段饱和度进行n等分,不同饱和度区间对应的交通状态记为η,η取值为1,…,n,根据路段交通量及行程时间调查数据,确定路段ai不同饱和度区间对应的行程时间分布函数fηi(ti,qi,Ci)。 Step1:确定路网拥堵状态。路网拥堵状态是路网中各路段交通状态的组合,若路段a1,a2,…,的交通状态分别是η1,η2,…,记路网拥堵状态为S(η1,η2,…)。根据路网拥堵状态即可确定路径的交通运行状态。 Step2:根据给定OD点对进行路径搜索,确定有效路径。 Step3:根据Δt定义确定时间单元Δt大小,并计算各路段的行程时间及概率。 Step4:根据出行者的参考点x0,由式(5)、式(6)计算各备选路径的主观效用,再由式(10)~式(12)计算主观概率和前景值。 Step5:出行者选取前景值最大的路径出行。 按照以上步骤,即可在给定的路网拥堵状态下,根据出行者的参考点,求得OD点对之间各条路径的前景值。 调查实际城市道路路段,从而得到不同拥堵状态的路段行程时间参数。选取合肥市徽州大道-太湖路交叉口为起点,马鞍山路-九华山路交叉口为终点,建立简单有向路网如图3。起终点间3条路径分别是:①起点-徽州大道-九华山路-终点;②起点-太湖路-马鞍山路-终点;③起点-靶场路-终点。 图3 有向路网Fig. 3 Directional road network 调查路网内9条有向路段的实时流量和行程时间,调查时段为06:00—24:00,根据Step0,n=3,饱和度区间为[0,0.2]、(0.2,0.6]和(0.6,1],对应的交通状态η取值分别为1,2,3。用正态分布函数表示各条路段行程时间分布,得到各路段不同拥堵水平下行程时间分布参数,如表1。 表1 路段行程时间分布参数Table 1 Distribution parameters of travel time of all road sections s 1)根据Step1,确定路网拥堵状态。为分析不同拥堵状态下的路径选择结果,结合实际路网交通特征,假定4种不同的路网拥堵状态: 状态1——S1(1,1,1,1,1,1,1,1,1),表示整体畅通的路网交通状态,各路段饱和度区间均为[0,0.2]; 状态2——S2(2,2,2,2,2,2,2,2,2),表示路网拥堵状态一般的水平,各路段饱和度区间均为(0.2,0.6]; 状态3——S3(2,3,2,3,2,3,2,2,3),表示局部拥堵的路网交通状态,部分路段饱和度区间均为[0.6,1]; 状态4——S4(3,3,3,3,3,3,3,3,3),表示整体拥堵的路网交通状态,各路段饱和度区间均为[0.6,1]。 2)根据Step2,确定4条有效路径。路径1: l1(a1,a2,a3,a4),路径2:l2(a1,a5,a6,a4),路径3:l3(a1,a5,a7),路径4:l4(a8,a9)。 3)根据Step3,根据路径行程时间均值,时间单元Δt=5s,由式(11)对路网中各条路段的行程时间分布离散化处理,并采用式(12)计算路径的行程时间所对应的概率。 取单位时间价值系数θ1=0.8、θ2=1.2、θ3=1.0[6],损失规避系数λ=1.15,效用敏感系数α=β= 0.8。 为了便于对比分析不同路径的前景值大小,假设出行者完成一次出行所花费的时间与心理预期时间相等的情况下,所获得的效用为0,即认为出行者恰好在预期行程时间完成出行时的收益xmax=0。 4)根据Step4,得到出行者在S1、S2和S3路网拥堵状态下,心理参考点x0与路径前景值V关系,如图4。 图4 前景值-参考点曲线Fig. 4 The relationship curves between reference points and prospect value 由图4可见,路网拥堵状态为S1时,路径1的前景值高于其他路径,如图4(a)。路网拥堵状态为S2,当参考点x0>-300时,路径4前景值最高;当参考点x0<-300时,路径1前景值最高,即高风险追求的出行者选择路径4出行,低风险追求的出行者选择路径1出行,如图4(b)。路网拥堵状态为S3时,路径3的前景值高于其他路径,如图4(c)。路网拥堵状态为S4时,路径1的前景值高于其他路径,如图4(d)。 由此可知,出行者路径选择结果不但与参考点的选取有关,而且与路网拥堵状态有关,出行者在不同时段出行,路径选择结果是不尽相同的。例如,路网状态3条件下,路径3前景值始终高于路径1前景值,反映到实际路网中,即路径3拥堵水平较低,出行者选择路径3出行所感受到的价值更高;而路网状态4条件下,路径3前景值始终低于路径1前景值,反映到实际路网中,即出行者选择路径1出行所感受到的价值更高。从行程时间均值亦可验证这一结论,路网状态3条件下,路径1行程时间均值为537 s,路径3行程时间均值为615 s,出行者更倾向于选择路径1出行。 基于累积前景理论,从路网及路段交通状态变化的角度探讨了出行者的路径选择行为,构建了前景值计算模型;结合算例分析了路径选择模型的应用方法与计算步骤,研究了不同路网拥堵状态下参考点的选取对路径选择结果的影响规律。结果表明:不同路网拥堵状态下路径选择结果不同。可见,路径前景值不但与参考点的选取有关,而且与路网拥堵状态有关。不同路网拥堵状态下,出行者路径选择结果不尽相同,表明考虑路网拥堵状态能更好地描述出行者的路径选择行为。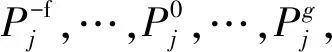


2 考虑路网拥堵的路径行程时间概率
2.1 路网拥堵状态对路径行程时间的影响
2.2 基于路段单元的路径行程时间概率函数
3 模型求解
4 算例分析

5 结 语

