自动驾驶汽车横向模糊控制器设计

邵毅明，陈亚伟

(1. 重庆交通大学 交通运输学院，重庆 400074； 2. 重庆交通大学 机电与车辆工程学院，重庆 400074)

随着智能技术发展，自动驾驶汽车已经成为汽车行业发展的新方向。运动控制是自动驾驶汽车研究领域的核心问题之一，其中横向控制则是运动控制的一个重要方面。横向控制可使车辆沿期望轨迹行驶，并在行驶过程中，保持车辆的稳定性和舒适性，它是实现车辆自动驾驶的基础。由于车辆在行驶过程中具有高度非线性动态特性及随机出现的外界干扰，故如何根据车辆实际情况设计出合理可靠的控制系统具有深远意义[1-3]。

笔者基于车辆动力学模型，充分考虑实际交通场景中的车辆状况，通过测试及总结熟练驾驶员操作经验，设计了车辆横向控制方案，并且利用模糊控制理论设计了横向模糊控制器。

1 建立车辆动力学模型

车辆是一个复杂的非线性系统。在建立车辆动力学模型时，既要保证车辆动力学模型尽可能准确，同时要对其适当的简化。故在建立模型之前做如下的假设:① 将前轮转向角作为输入；② 假设车辆只做平行于地面的运动；③ 忽略空气阻力的影响；④ 认为地面切向力不影响轮胎侧偏特性；⑤ 认为汽车行驶过程中轮胎特性不变。

根据上述假设，建立如图1的车辆二自由度单轨模型，对在水平路面行驶的车辆建立惯性坐标系OXYZ和车辆局部坐标系oxyz，并在此基础上对其做动力学分析。图1中的符号含义如表1。

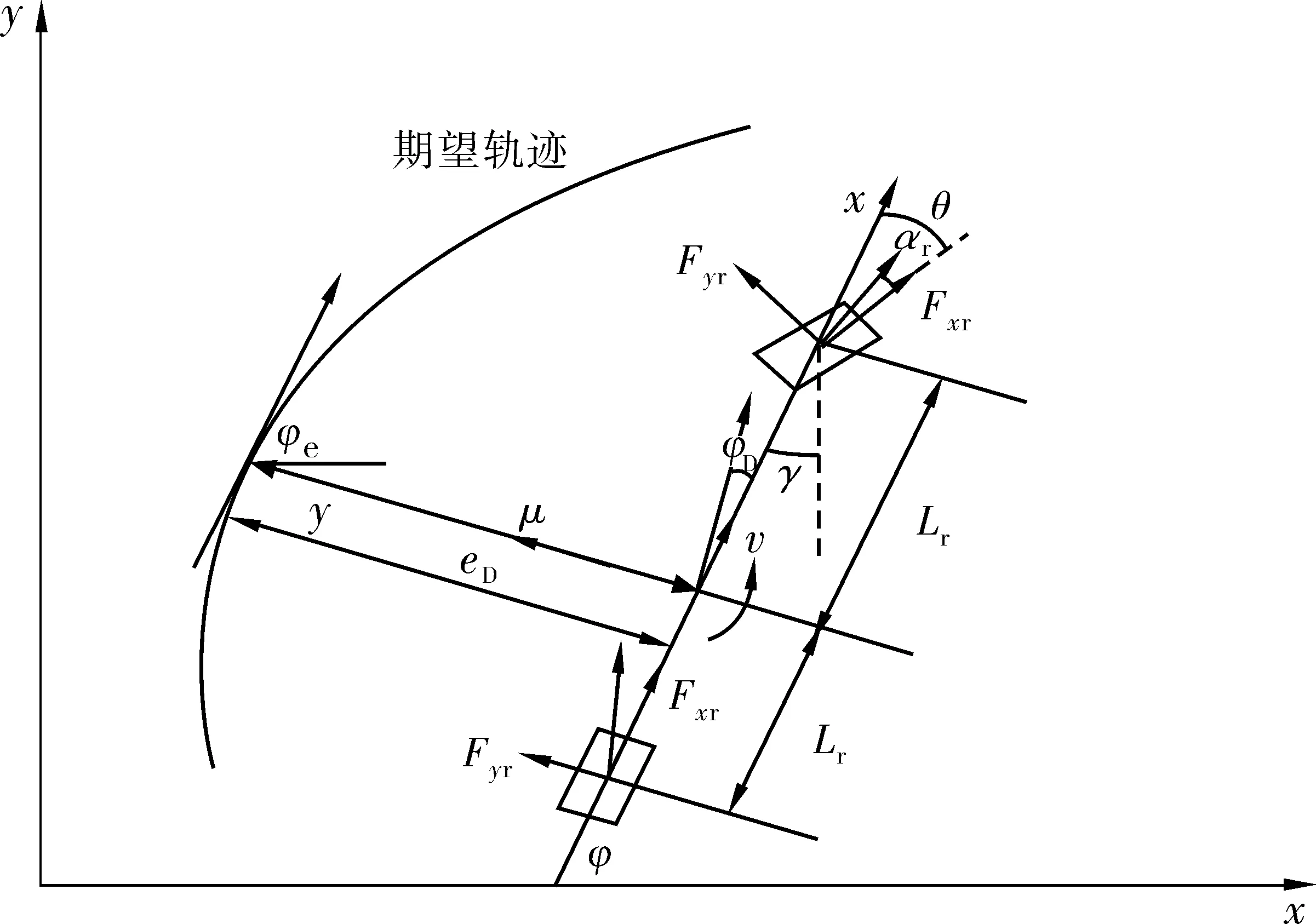
图1 车辆动力学模型Fig. 1 Vehicle dynamics model

指 标桥形标A均值M标准差SD桥形标B均值M标准差SD桥形标C均值M标准差SD桥形标D均值M标准差SDSig.眼跳次数/次18.2676.28519.6676.92520.1336.46822.4675.4100.003∗∗总注视次数/次26.4004.74826.9335.16127.5336.40227.9334.3010.761∗∗兴趣区内注视次数/次19.7335.75020.8005.32123.0675.92224.1334.4060.002∗∗总注视时间/s7.2502.0337.4682.2366.5851.8837.0151.3600.408∗∗平均注视驻留时间/s0.3020.1250.2800.0660.2440.0540.2620.0480.082∗∗第一注视点时间/s0.5170.4030.3150.1490.3040.2340.2770.1950.032∗∗

根据牛顿第二定律，列出如下车辆横摆运动、纵向运动以及横摆运动方程，如式(1)～(3)：

(1)

(2)

(3)

由于侧偏角在小幅度范围内，侧向力随侧偏角线性上升，此时车辆前后轮胎受到的侧向力可近似表示如式(4)：

Fyf=kfαf；Fyr=krαr

(4)

前后轮侧偏角分别可表示如式(5)、(6)：

(5)

(6)

将式(5)、(6)与式(1)～(3)联立可得车辆横向动力学模型，如式(7)：

(7)

车辆循迹过程中，横向误差可表示如式(8)、(9)：

(9)

(10)

(11)

式(7)所表示的车辆横向动力学模型可改写如式(12)：

(12)

(13)

2 车辆横向模糊控制研究

在得到车辆横向动力学模型均是基于车辆匀速行驶并且在小转角的情况下，只适用于道路平坦通畅，并且无较大转角的场景。但实际上车辆所处的交通环境极其复杂，经常需要更改路径，频繁的变换速度，这种情况下上述关于车辆动力学的假设将无法成立，实际交通环境下的车辆会存在较多不确定因素，如系统模型参数的改变、未建模部分的影响、不可预测的外界干扰输入等[4-7]。

故横向控制系统必须具备在模型不精确或者其他外界条件干扰下，依旧有良好的自适应性，以便完成控制任务。同时对参数、外界条件变化的情况，还必须具备一定的鲁棒性。考虑到车辆横向控制的具有复杂性、行驶过程的非线性以及难以建立精确的数学模型等特点，笔者引入模糊控制方法。模糊控制能够模拟人的行为，且不需要对控制对象精确建模，它是解决难以精确建模复杂非线性问题的有效手段[8-10]。

车辆在行驶过程中，控制系统要实时获取外界环境和车辆状态两方面信息，控制系统流程如图2，模糊控制器将两部分信息融合，通过模糊控制器的推理机进行分析，最后输出合适的前轮控制量，从而达到车辆横向控制的目标。

图2 控制系统Fig. 2 Control system

2.1 模糊控制原理

模糊控制的思想是将熟练人员的经验总结为一系列的控制规则，再通过模糊推理得到合理的控制量作用于控制对象[11]。

模糊控制系统的关键部件是模糊控制器(图3)，它由以下几部分组成：

图3 模糊控制器结构Fig. 3 Fuzzy controller structure

1)模糊化接口：模糊化接口将输入变量转变为模糊矢量，以便控制器对其进行求解。

2)模糊数据库：模糊数据库的作用是在规则推理时向推理机提供数据。

3)规则库：规则库存放模糊规则，主要由熟练人员的经验总结而来，通过一系列的关系词连接而成。

4)推理机：推理机经过逻辑运算按照制定的模糊规则将输入的模糊变量输出。

5)解模糊化接口：解模糊化是将输出的模糊量经过运算转变为精确量的过程。

2.2 模糊控制器的设计

模糊控制器的设计主要包括：确定输入输出变量、模糊化、制定模糊控制规则、模糊推理和解模糊化等过程[12]。

2.2.1 确定输入和输出变量

模糊控制器的设计首先必须确定输入和输出变量。车辆在行驶过程中，所能获得的数据一般有横向误差和横摆角偏差以及两者的变化率，车辆可依靠以上信息进行横向操纵控制。为降低模糊控制的输入维数，笔者以横向误差和横摆角偏差为输入变量，前轮转向角为输出变量[13]。

2.2.2 模糊化

选取横向误差eD，横摆角偏差φD和前轮转向角θ这3个语言变量的模糊论域为[-3，-2，-1,0,1,2,3]，对3个变量论域取7个模糊子集，即PB(正大)、PM(正中)、PS(正小)、ZO(0)、NS(负小)、NM(负中)、NB(负大)。

eD>0表示车辆在道路中心线右侧；eD=0表示车辆正位于道路中心线；eD<0表示车辆在道路中心线左侧。

u>0表示前轮右转；u=0表示不改变方向；u<0表示前轮左偏。

3个变量的模糊子集采用gaussmf型和trimf型。

2.2.3 制定模糊控制规则

模糊控制规则指通过模糊逻辑的模糊条件语句来表征人类驾驶行为的经验知识，笔者基于试验和熟练驾驶员日常经验，制定了49条“IF-THEN”规则，图4为隶属度函数，图5为MATLAB中模糊规则的编辑器。表2是制定的模糊控制规则，如下：

Ri:IFeDisEiandφDisEci,THENθis Si

其中：Ei、Eci和Si分别为输入变量eD、φD和输出变量θ模糊子集的语言变量，{Ei,Eci,Si}∈{NB,NM,NS,ZO,PS,PM,PB}。

图4 隶属度函数Fig. 4 Membership function

图5 规则制定Fig. 5 Rule making

uφDNBNMNSZOPSPMPBeDNBNBNBNMNMNSNSZONMNBNMNMNSNSZOPSNSNMNMNSNSZOPSPSZONMNSNSZOPSPSPMPSNSNSZOPSPSPMPMPMNSZOPSPSPMPMPBPBZOPSPSPMPMPBPB

2.2.4 模糊推理

笔者采用Mamdani的max-min合成法，具体步骤如下[14]：

把规则库中的Ei、Eci和Si分别看作输入变量eD、φD和输出变量θ对应论域X、Y、Z上的词集，可得如下的控制规则关系：

Ri=(Ei×Eci)×Si

Ri的隶属函数为：

μRi(x,y,z)=μEi(x)∧μEci(y)∧μSi(z)

其中：∀x∈X,∀y∈Y,∀z∈Z

R的隶属度函数为：

当输入变量eD、φD分别取模糊集E、Ec时，控制量为：

S=(E×Ec)°R

因此，S的隶属度为：

2.2.5 解模糊化

上述模糊推理得到的是模糊值，必须通过解模糊转化为实际控制值输出。解模糊化是将模糊控制量转化为精确量，然后乘以比例因子转化为实际的控制量。笔者选用centroid法(面积中心法)进行解模糊，求得反映控制量的真实值[15-16]。

如果已知横向误差eD及横摆角偏差φD，则先通过量化因子k1和k2将其范围限定在模糊论域内，将其模糊化，再通过解模糊得到模糊控制器的输出值，如表3。

表3 模糊控制Table 3 Fuzzy control

经过上述步骤，基于MTALAB完成了笔者所需的模糊控制器设计，模糊控制系统结构如图6。

图6 模糊控制系统结构Fig. 6 Fuzzy control system structure

3 不同工况的仿真研究

通过Carsim和MATLAB进行联合仿真，通过观察车辆在不同车速下沿着期望轨迹的行驶状况，以验证所设计控制器的有效性。

3.1 仿真道路曲率

仿真路径曲率如图7。

图7 道路曲率Fig. 7 Road curvature map

开始时路径为直线以便监测横向控制器循迹的性能；然后，从100 m路段开始，路径由两段方向相反的弧线组成，用来分析控制器循迹弯道的性能；随后，是一段曲率为零的路段；最后经过一段曲率变化较大的弧线段，以检验控制器在急速转弯时的性能。

考虑到速度对车辆横向控制有重要影响，笔者选取30 km/h作为低速工况下的测试速度，高速工况选择60 km/h作为测试速度，分别以上述速度进行仿真实验。

3.2 低速工况的仿真

起始工况：θ=-3°，v=30 km/h，以车辆横向误差、横摆角偏差、横向加速度以及前轮转角作为观测量，得到如下仿真曲线，见图8。

图8 速度为30 km/h时的仿真曲线Fig. 8 The simulation curve when the speed is 30 km/h

由图8(a)可知：最大稳态误差发生在曲率为-0.001 5 m-1路段，曲线最大稳态误差为-0.025 m，响应速度较快；由图8(b)可知：模糊控制器可将横摆角偏差控制在一定范围内，超调量和振荡较小，最大横摆角偏差不超过1°；由图8(c)知：在速度较低时，即使在路径曲率快速变化的恶劣工况下，模糊控制器仍然可以控制车辆在一定的舒适度范围之内，横向加速度最大不超过0.025 m/s2；由图8(d)可知：模糊控制器可保证前轮转角平滑输出且稳定性较高，最大前轮转角不超过3°；由图8(e)可知：在低速工况下，车辆横摆角速度变化不大，最大横摆角速度不超过10 deg/s,超调量较小；由图8(f)可知：质心侧偏角变化趋势较为平缓，最大侧偏角不超过3 deg，没有局部振荡的现象发生。

3.3 高速工况的仿真

初始状态：θ=-3°，v=60 km/h。同样以车辆横向误差、横摆角偏差、横向加速度以及前轮转角作为观测量，得到如下仿真曲线，见图9。

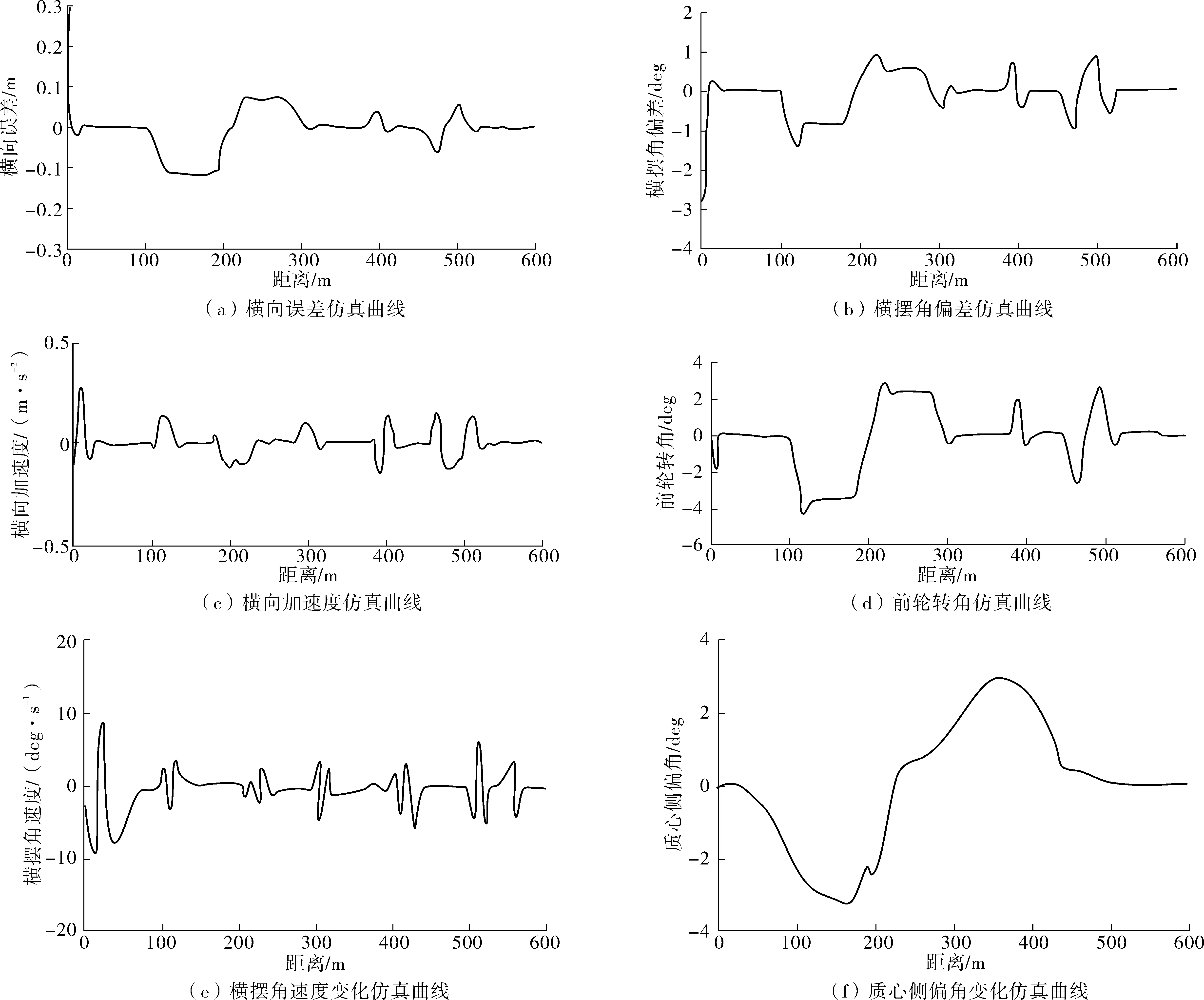
图9 速度为60 km/h时的仿真曲线Fig. 9 The simulation curve when the speed is 60 km/h

由图9(a)可知：曲率为0.015-1处路段车辆的稳态误差最大，最大稳态误差为0.1 m；由图9(b)可知：模糊控制器调节横摆角偏差的时间短，且控制精度较高，最大横摆角偏差不超过1.25°；由图9(c)可知：在初始纠正偏差和曲率快速变化的阶段，车辆的横向加速度较大，但模糊控制器的振荡较小，有较好的乘坐舒适性；由图9(d)可知：控制输出量的振荡较小，前轮转向角最大为不超过4″。由图9(e)可知：虽有部分振荡现象发生，但车辆横摆角整体变化幅度较小，其幅值仍未超出10 deg/s，车辆没有失去稳定性；由图9(f)可知：在模糊控制器的作用下，质心侧偏角保持在±3 deg范围内，并且没有急速骤变的情况发生，能够保证车辆的稳定性。

综上所述，笔者设计的模糊控制器具备较好的动态响应特性和循迹精度，在车辆循迹曲率变化工况下，系统响应较快，能够准确的跟随目标轨迹，而且稳态误差不随道路曲率变化而发生较大的起伏，具备一定抗干扰能力。

4 结 语

笔者建立了车辆二自由度单轨模型，考虑到车辆横向控制为非线性的时变复杂过程，将驾驶员实际经验与模糊控制理论相结合，设计了车辆横向模糊控制器。经过理论分析以及模拟仿真，车辆的横向误差、横摆角偏差等参数在一定范围之内，仿真结果表明：在一定速度范围内，无论是直线路段还是弯道，设计的模糊控制器均能够使车辆平稳快速的跟随目标轨迹行驶。