基于Drucker-Prager Cap模型的装配式混凝土箱涵节段滞回性能研究

杜 青，郝景钊，卿龙邦

(河北工业大学 土木与交通学院，天津 300401)

0 引 言

以往，在高速公路以及其他道路施工中的过水涵洞和通道多采用现浇箱涵，而预制装配式混凝土箱涵在我国的的应用尚处于初级阶段。随着国家对装配式建筑的大力推广，装配式箱涵在道路工程、地下结构等方面的应用将会越来越广泛。装配式箱涵具有施工周期短，质量控制好，生产要素少，经济效果好，环境影响小等特点，利于工厂化和标准化施工，可以在城区、高寒地区、沙漠戈壁等对施工环境要求较高的区域广泛应用，具有很好的推广应用前景[1]。而与之相对应的理论计算却相对缺乏，对于地震对箱涵的影响程度，以及作为地下结构的箱涵应确保的抗震性能也不明确。

为了获得装配式钢筋混凝土箱涵拼装节段的抗震性能，笔者利用了分析软件ADINA建立了有限元模型，但在计算过程中发现在滞回性能分析中比较难收敛。而ADINA提供的非协调参数Drucker-Prager Cap(D-P Cap)模型作为一种经典有效的非线性本构模型，具有破坏规则简单、控制参数明确、收敛性强、计算速度快等特点[2]。然而该模型多用于对岩土材料的模拟，相关参数的确定准则并不适用于混凝土材料。通过参阅相关文献和大量试算，确定了适用于混凝土材料的相关参数，并通过与试验结果对比，验证了非协调参数D-P Cap模型对混凝土的模拟在预制箱涵拼装节段滞回性能分析时的准确性。

1 试验体参数及实验过程

1.1 试验体参数及配筋图

1.1.1 试验体尺寸及配筋图

试验体为大跨度浅埋式箱涵的缩尺模型，形状为矩形，净跨为4 m，净高为2 m，宽为0.8 m。具体尺寸及配筋图如图1、图2。

图1 试验体尺寸Fig. 1 Size of the specimen

图2 钢筋尺寸及分布位置Fig. 2 Size and distribution position of rebar

1.1.2 材料参数

选用的混凝土及钢筋材料参数实验测得数值如表1、表2。

表1 混凝土材料参数Table 1 Material parameters of concrete

表2 钢筋材料参数Table 2 Material parameters of rebar

1.2 荷载及加载方式

为了模拟箱涵结构在地下的安装条件，在箱涵下部角部两侧设置支撑，使得垂直和水平方向上不会产生拉力，同时也不会限制底板和侧壁的弯曲。液压伺服机构通过连杆和夹具与实验体连接，使得水平荷载施加在箱涵顶板的轴线上。

竖向荷载通过对PC钢棒施加预应力，从而在箱涵顶板处施加两点式集中荷载，用以模拟上部覆土的均布荷载。加载位置、荷载大小及加载制度见图3、图4。图4中：n为加载周期；r为层间位移角，r=δ/H。

图3 试验体荷载施加位置及荷载大小Fig. 3 Position and size of the load on the specimen

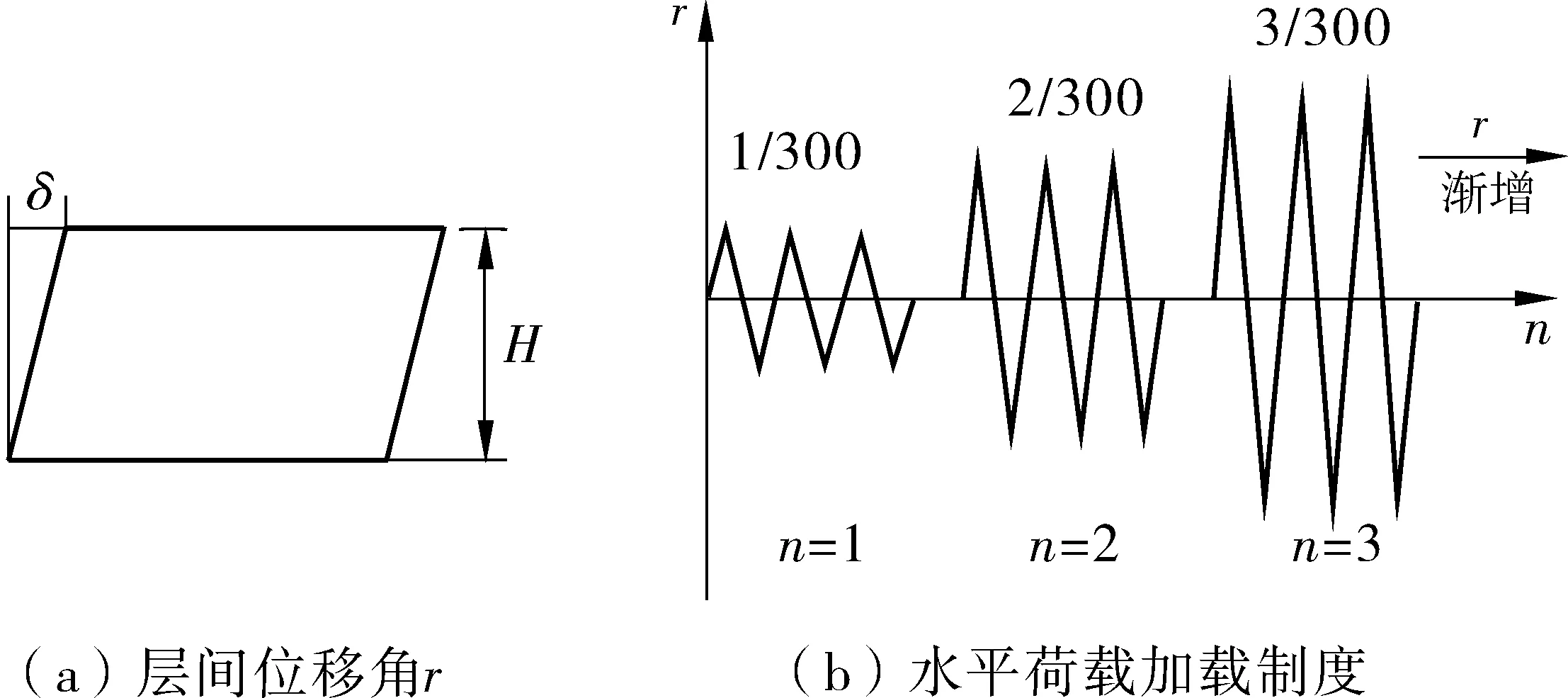
图4 层间位移角及水平荷载加载制度Fig. 4 Interstory displacement angle and loading system underhorizontal load

2 有限元模型

2.1 几何模型及网格划分

ADINA提供了Native与Parasolid两种几何建模方式。对于钢筋，笔者采用Native建模方式，即点-线建模。而由于混凝土模型较为复杂，为便于各部分的网格连接，对于混凝土，采用Parasolid建模方式，即定义Sheet后并划分网格，通过拉伸命令同时定义单元属性，使得整个混凝土模型的网格完美连接在一起，从而避免导致计算错误。此外，通过前期规划，使得钢筋单元节点与混凝土单元节点重合在一起，从而压缩节点个数，减少计算量。模型中混凝土单元采用六面体八节点的3D-solid单元，钢筋采用两节点的Truss单元，具体模型见图5。

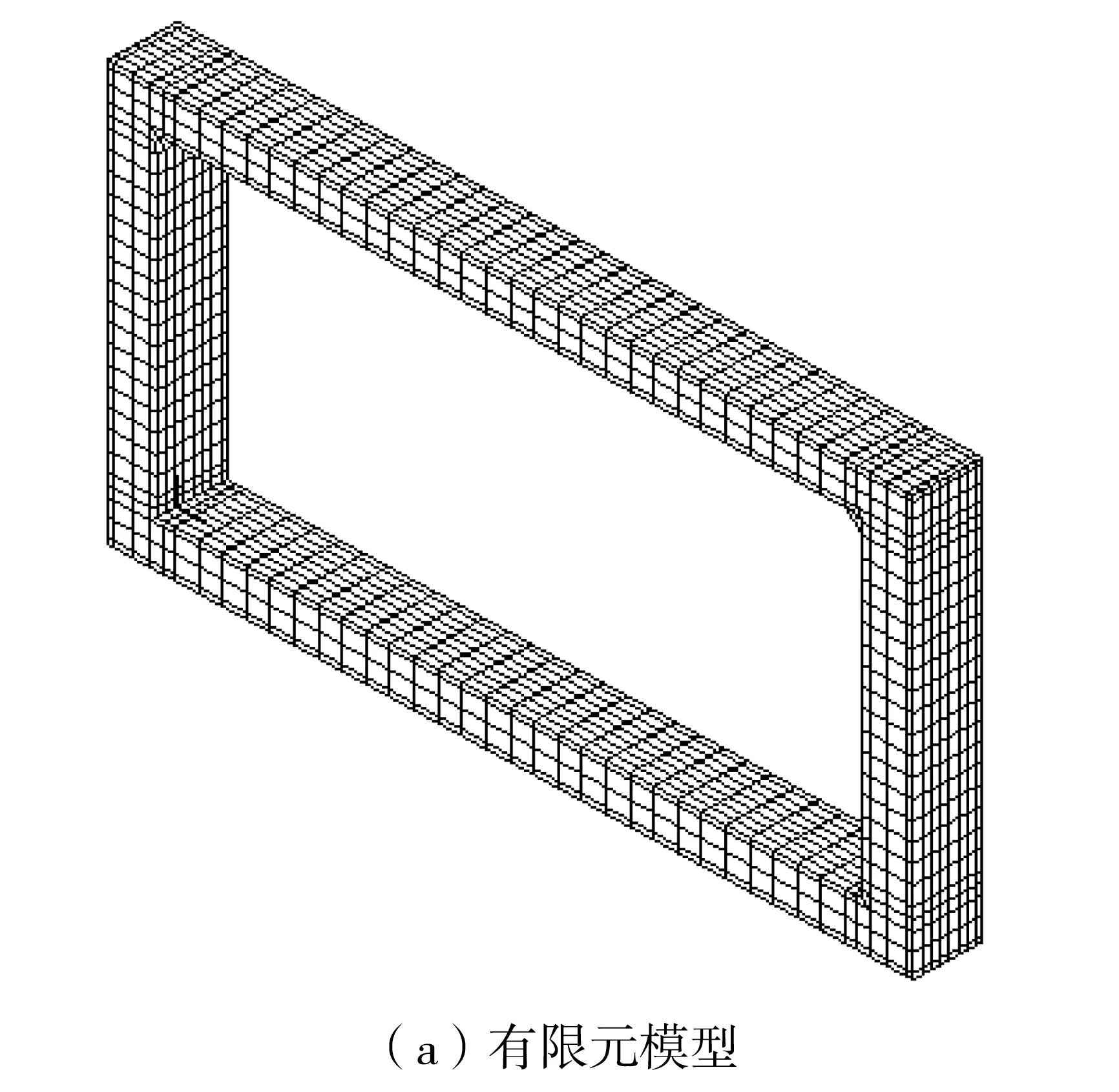
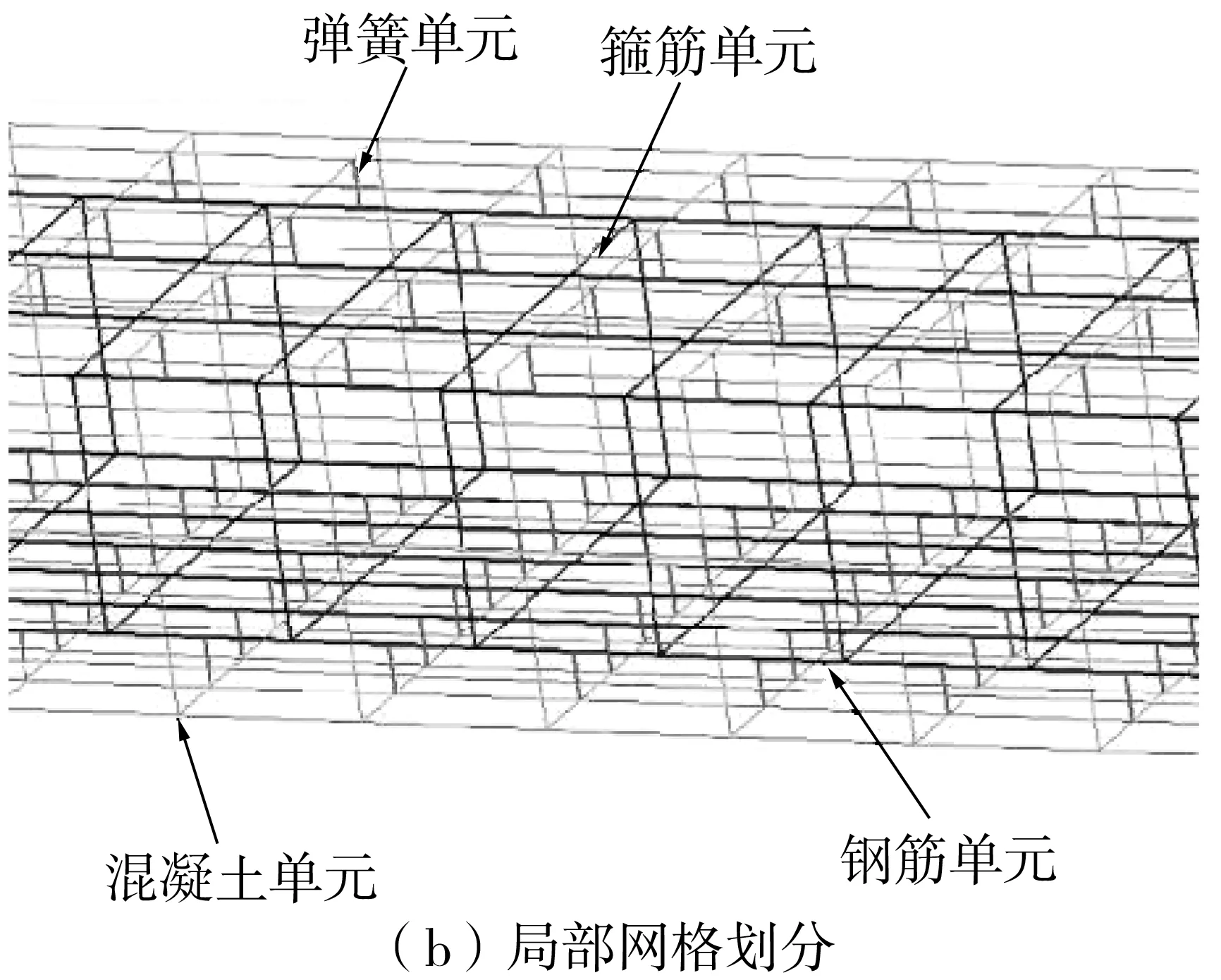
图5 有限元模型及网格划分Fig. 5 Finite element model and mesh generation

2.2 本构模型

2.2.1 混凝土本构模型

采用ADINA提供的非协调参数D-P Cap模型对混凝土进行模拟。D-P Cap模型基于理想Drucker-Prager屈服函数以及拉伸截止、帽盖硬化等准则，即在经典的D-P模型基础上，分别在静水压力轴的两端增加拉伸中止屈服面和压缩帽盖屈服面，利用这两个屈服面可以较好地模拟混凝土受拉受压破坏。

1)Drucker-Prager屈服条件

在D-P Cap模型中Drucker-Prager屈服条件由式(1)给出：

(1)

式中：I1为应力张量第一不变量；J2D为应力偏量第二不变量；α、k由式(2)给出[3]:

(2)

式中：c为内聚力；φ为内摩擦角。

图6 子午面上的D-P Cap模型Fig. 6 D-P Cap model in meridian plane

参考文献[4]列出的不同强度下混凝土粘聚力和内摩擦角，计算α值约为0.35。但混凝土与岩土材料不同，考虑到真实结构中的钢筋混凝土构件在工作时多处于无围压状态，且由该方法得到的屈服准则无法兼顾混凝土的受拉受压性能，过高的α值会使混凝土在偏大的范围内按线弹性计算，最终使得结果误差过大。而鉴于实际工程中的混凝土材料受静水压力并不明显，需要通过控制参数α的大小适当限制其圆锥面的张角。经过大量试算，当α值处于0.10～0.12之间时，计算结果较为准确，取α=0.115。而参数k的物理意义较为明确，即混凝土材料在纯剪应力下的屈服应力。按照矩形短梁的纯剪试验结果，取k=(0.17-0.25)fc[5]，经大量试算，取k=0.23fc。

2)帽盖硬化段

在Drucker-Prager屈服函数引入帽盖的目的是为了考虑静水压力导致材料空隙破坏，从而出现体积屈服的现象。笔者采用平面帽盖模型，屈服函数：

fc=I1-X

(3)

(4)

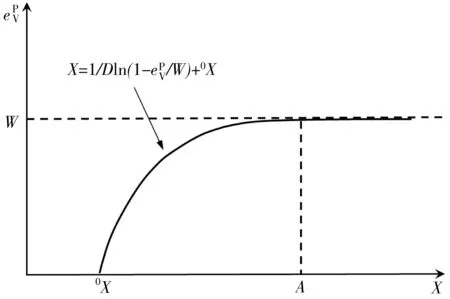
图7 帽盖位置X与体积塑应变的关系Fig. 7 Relationship between cap position X and volumetric

在ADINA中的D-P Cap模型中，帽盖硬化段最重要的部分为0X、W、D等3个参数的确定。文献[6]提供了0X的拟合式：

0X=13.14+1.9fc

(5)

文献[6]也给出了W的参考值为0.067[6]。而文献[3]也表明，W在0.066～0.18之间变化，D在0.000 953～0.0 711 MPa-1之间变化。通过大量试算，取W=0.067，D=0.001 MPa-1。

2.2.2 钢筋本构模型

钢筋采用Bilinear Elastic-Plastic双线性本构关系模型。该本构模型基于Von-Mises屈服条件、相关流动法则、等向应变硬化或随动应变硬化条件。其中，将纵筋等主要受力钢筋通过弹簧单元与混凝土单元连接在一起，箍筋等辅助钢筋通过use as rebar选项与混凝土单元耦合在一起。此外，在钢筋屈服后，弹性模量将降为初始模量的1/100[7]。本构关系如图8。

图8 钢筋本构模型Fig. 8 Constitutive model of rebar

2.2.3 钢筋与混凝土粘结滑移关系

在钢筋混凝土结构拟静力试验中，钢筋和混凝土之间会发生粘结滑移，此为滞回曲线出现捏拢现象的重要影响因素。对粘结滑移现象模拟准确与否将对结果产生巨大影响。当前钢筋混凝土粘结滑移本构关系的表达式有很多，如H. NILSON通过对B.BRESLER等的拉伸试件试验分析，拟合得到粘结滑移关系经验表达式[8]；S. M. MIRZA根据变形钢筋模拟缝间粘结强度的试验结果得到四次多项式等[9]。笔者采用前者研究所得经验表达式作为粘结滑移本构模型，即：

τ=9.78×102s-5.72×104s2+8.35×105s3

(6)

式中：τ为粘结应力，MPa；s为相对滑移量，mm。

此类型粘结滑移作用可以通过在模型中钢筋节点与混凝土节点之间设置的弹簧单元来模拟。弹簧为假想的力学模型，具有弹性刚度，但并没有实际尺寸，因此，可以设置在需要设置联结的任何地方，使得建模方便，形式简单，是有限元模拟中常用的一种方法[10]。

2.3 加载方式及加载制度

在原试验中，通过控制箱涵试件的层间位移角的方式进行低周往复加载。此种方式在模拟分析中难以实现，因而将其转换为由位移控制的加载方式，并施加于箱涵模型顶板轴线位置。

3 结果分析

3.1 滞回性能对比

数值模拟的水平荷载-顶板左端水平位移曲线与实验曲线对比见图9。

图9 荷载-位移曲线Fig. 9 Load-displacement curves

由图9可知，数值模拟结果与试验结果吻合度较高，刚度退化和强度退化现象得到了较为准确的展现，滞回曲线的捏拢现象明显准确，证明了模型的准确性及参数设置的合理性。而在结构被施加负向位移时模拟计算结果略低于实验值，可能因为原模型采用层间位移角控制施加荷载，与笔者位移控制施加荷载的方式有所不同，从而导致结果略有差异。

3.2 骨架曲线

骨架曲线是指往复加载时各次滞回曲线峰点的连线。如图10，对比试验结果与计算结果可见，两者总体吻合度较高，变形能力模拟较为准确。此外，计算结果的屈服承载力与极限承载力与试验结果较为接近，而最大承载力则较低，偏于安全。

图10 骨架曲线Fig. 10 Skeleton curve

3.3 残余位移

残余位移及结构卸载后产生的不可恢复变形为评价结构修复性的重要指标。由表3可见，残余位移计算结果与试验结果十分接近，仅最后一个循环差距稍大。

表3 残余位移Table 3 Residual displacement mm

3.4 应力云图损伤对比

将应力云图显示上限调整到混凝土屈服强度附近后，显示断面、侧壁与顶板应力云图如图11～图13。由图11～图13可见，试验中试件损伤位置与应力云图中应力集中位置基本一致。

图11 断面损伤对比Fig. 11 Contrast of specimen damage for cross-section

图12 侧壁损伤对比Fig. 12 Contrast of specimen damage for side wall

图13 顶板损伤对比Fig. 13 Contrast of specimen damage for top slab

4 结 语

笔者通过对大跨度浅埋式预制混凝土箱涵的滞回性能进行数值模拟分析，从数值计算结果与实际试验结果的对比中得出以下结论：

1)模型的建立过程合理，计算结果与试验值吻合度较高，比较准确的反映了预制箱涵构件的抗震性能和滞回性能，基本再现了结构的破坏状况。

2)通过阅读相关文献和大量试算所确定的参数，使得在ADINA中的D-P Cap模型对混凝土模拟得到较为准确的结果。该成果可用于预制箱涵等混凝土结构的抗震计算和设计。