波纹腹板H形钢梁承载力的参数化分析

王浩瀚，赏锦国

（1.广东省建筑设计研究院，广东 广州 510000；2.安徽省城建设计研究总院股份有限公司，安徽 合肥 230000）

1 概述

随着波纹钢腹板组合梁桥的推广和应用，因H形钢的波纹腹板较普通的平腹板有着良好的受力性能和明显的经济效益[1-2]，因此对其腹板承载能力和稳定性进行参数化分析，对以后的研究和应用具有一定的参考价值。

H型钢的波纹腹板构造见图1，它包括厚度t、平折板宽度a、斜折板宽度c、倾角α、斜折板纵向投影长度b和波高d，其中的l=2（a+b）。

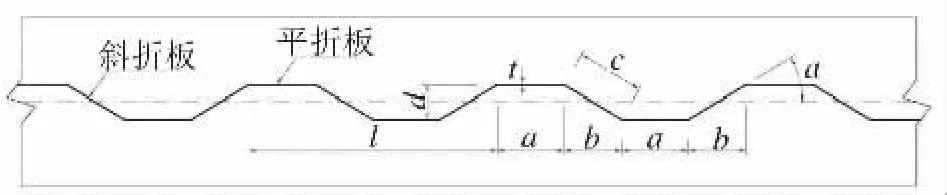
图1 H型钢波纹腹板构造

2 有限元建模

采用ANSYS有限元软件对焊接波纹腹板H形钢梁进行分析，对比各种参数变化对波纹腹板极限承载能力的影响，这些参数包括腹板厚度t、倾角α、平折板宽度a和材料屈服强度σy。

2.1 单元的选取

根据结构的受力特性，采用曲壳模型4节点壳单元shell181建立波纹腹板H形钢梁模型，该单元每个节点有6个自由度，具有大变形功能[3]。该单元具有强大的非线性功能，其几何特征如图2所示。

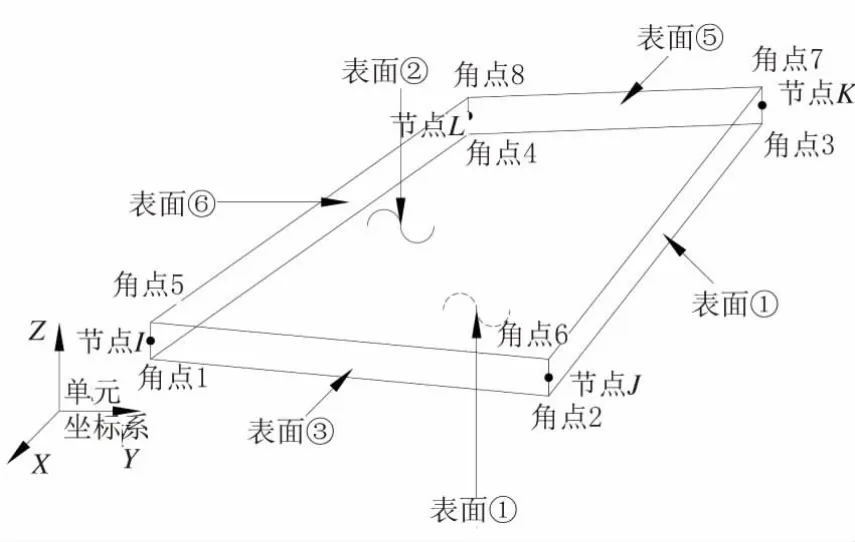
图2 Shell181单元几何特征

2.2 非线性问题

波纹腹板稳定性计算中，腹板发生屈曲时已有较大的变形，相对于腹板的几何尺寸不可忽略，应考虑腹板几何非线性的影响。

如果结构经受大变形，会引起结构的非线性响应。当达到极限状态时，腹板某部分将进入塑性状态，因此本计算中除了材料非线性（即材料本构关系）外，还应考虑几何非线性。

本次计算中采用简化的三折线模型，即：基于连续屈服理论的应力-应变曲线、基于非连续屈服理论的应力-应变曲线和理想弹塑性体应力-应变曲线，其曲线图见图 3（a）、图 3（b）和图 3（c）。

3 几何参数分析

3.1 腹板厚度的影响

采用的有限元模型如图4所示；平折板宽度a与斜折板宽度c均为66 mm，腹板高度h为330 mm，弹性模量 E=2.05×105N/mm2，泊松比 μ=0.3，屈服强度 σy为 261 MPa。

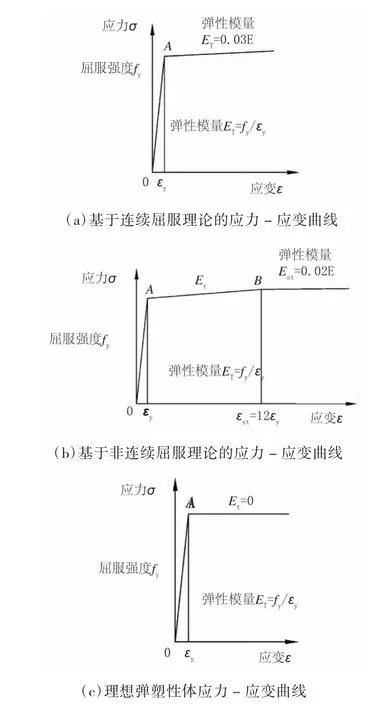
图3 钢材的应力-应变曲线

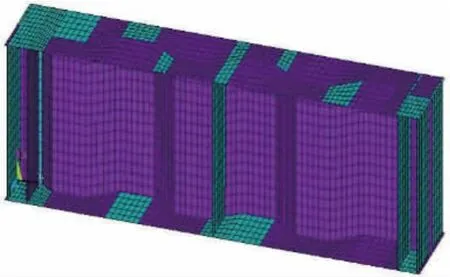
图4 有限元模型

以腹板厚度t为变量，取值范围为1～4 mm，变化幅度为0.5 mm，此时腹板的抗剪极限承载能力Q 为板厚 t的函数，即 Q（t）。

模型分析结果均有同样的屈曲模式，其中t=3 mm、4 mm时的屈曲模式如图5所示。

当腹板高度h为330 mm时，随着腹板厚度t的变化，其极限承载力对比见表1。

由表1可知，腹板极限承载力模型分析值随腹板厚度增加而明显增加。本次计算结果拟合后的曲线如图6所示，可以发现其极限承载力Q与腹板厚度t的关系为：

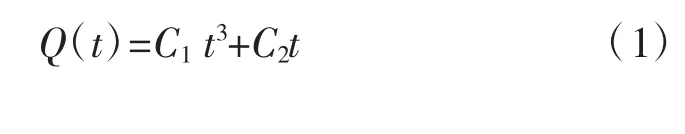
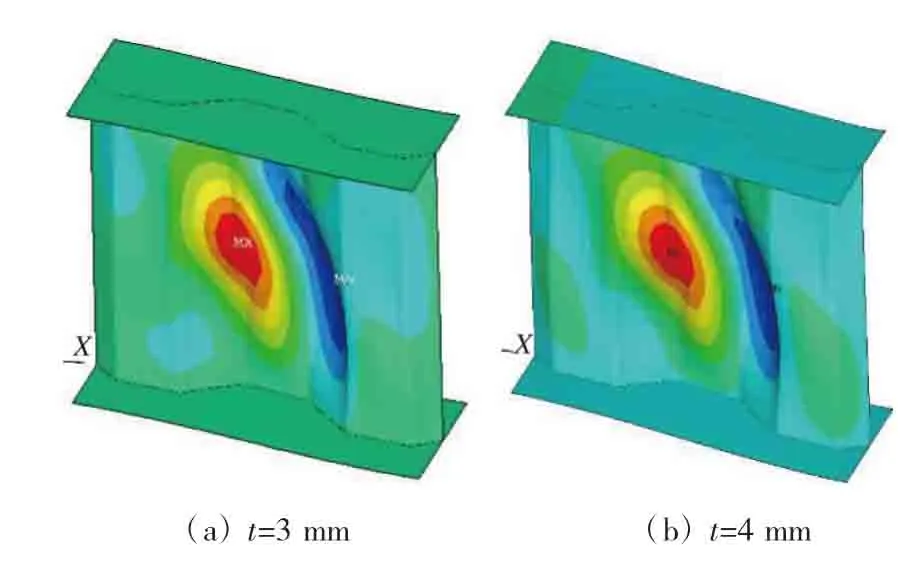
图5 不同板厚的屈曲模式

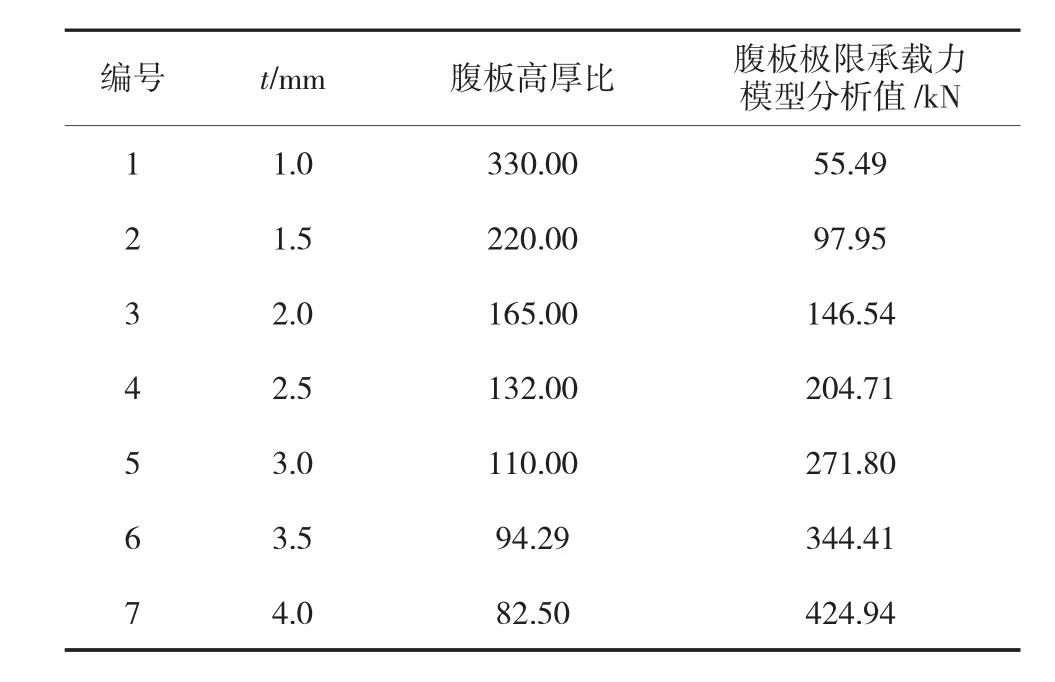
表1 腹板厚度变化时的腹板极限承载力

式中：C1、C2分别为调整系数。

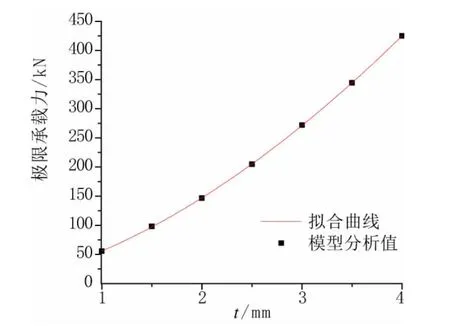
图6 不同腹板厚度下的腹板极限承载力

3.2 波纹形状的影响

如图1所示，波纹腹板形状参数有平折板宽度a、斜折板宽度c、斜折板纵向投影长度b、波高d和波纹倾角α。若假设a=c，根据几何条件有sin α=则此时波纹腹板形状独立参数仅剩折板宽度a和倾角α。

3.2.1 折板宽度a不变，以倾角α为变量时的极限承载力

采用如图7所示的有限元模型分析，腹板高度h为341 mm，折板宽度a=c=66 mm，屈服强度为325 MPa，腹板厚度t为3.0 mm。以倾角α为变量（sin α=0.26，0.50，0.61，0.71，0.87，0.97），模型分析结果中sin α=d/a=0.71时的屈曲模式见图8。

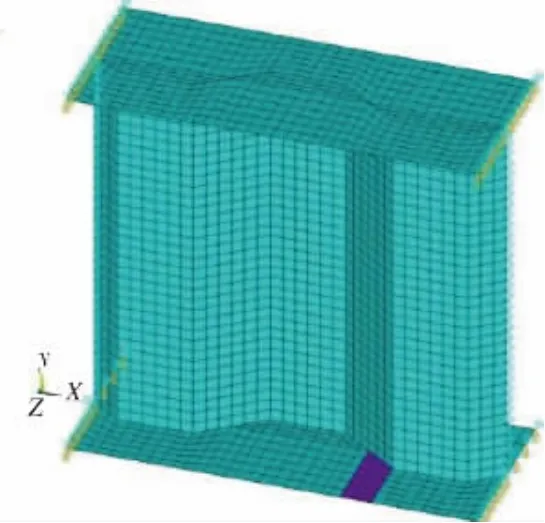
图7 简化有限元模型

图8 sin α=d/a=0.71的屈曲模式

当折板宽度a=c，在保持其他参数不变的情况下，以倾角α为变量，其腹板的极限承载力对比见表2。

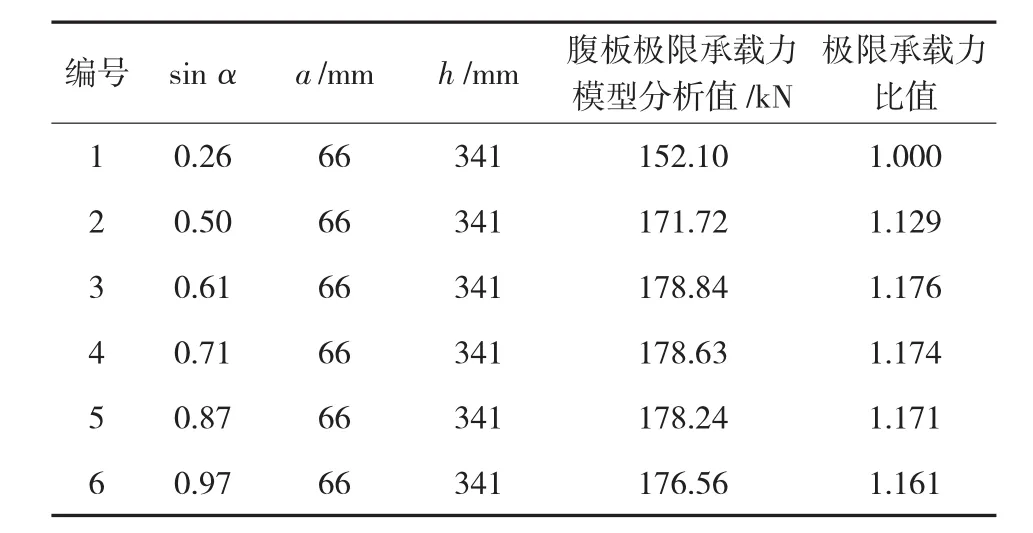
表2 波纹倾角变化时的腹板极限承载力

由表2可知，当sin α≤0.61时，随倾角增大，侧向约束增强，腹板的极限承载力也逐渐增大；当sin α为0.61～0.71时，模型取得较高承载能力；当sin α＞0.71时，随倾角的进一步增加，腹板的承载能力变化不大，同时将导致腹板的钢材用量增加。

3.2.2 倾角α不变，以折板宽度a为变量时的极限承载力采用如图9所示的有限元模型，模型总长L为480 mm。此时平折板宽度a与斜折板宽度c相等，a=c，以 a为变量（a=11，22，33，44，66，88，132 mm）。

模型总长L不变且sin α=0.61，当a较小时，模型的波纹变密，见图9（a）；当a较大时，模型的波纹变疏，见图 9（b）。

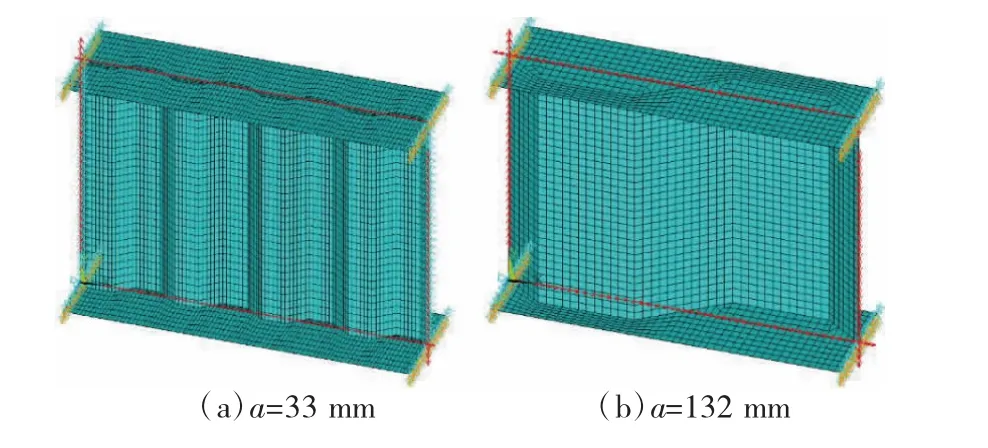
图9 折板板幅变化时的有限元模型

当a为不同值时，其折板有不同的屈曲模式，如图10所示；折板板幅变化时的腹板极限承载力见表3。

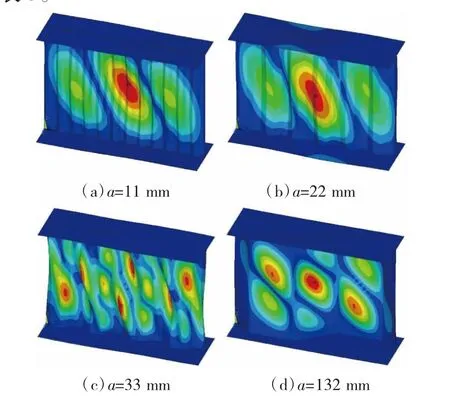
图10 不同折板宽度屈曲模式

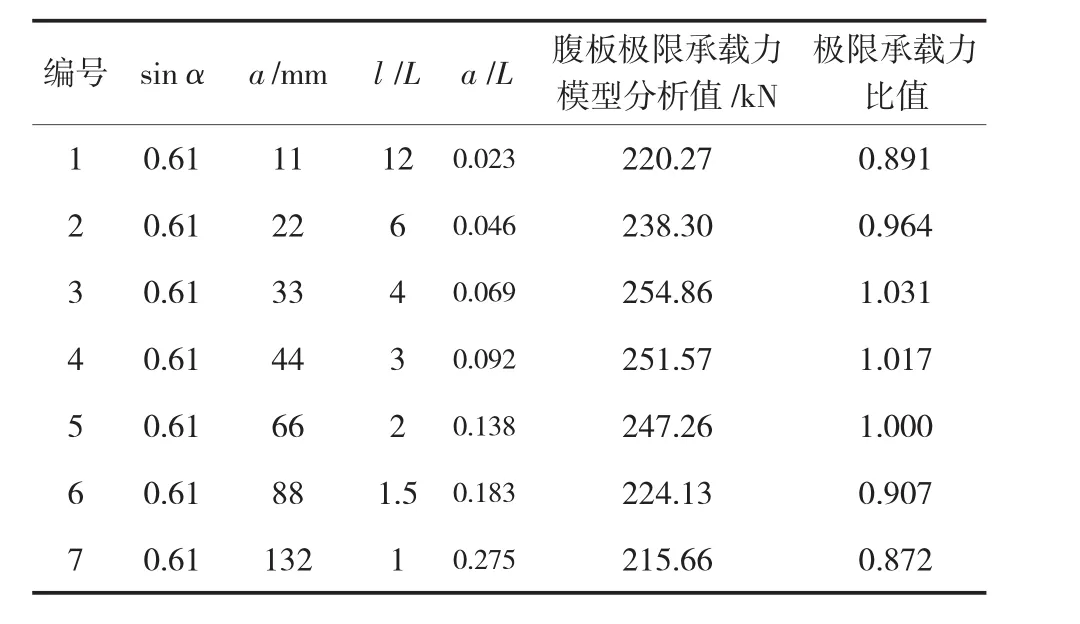
表3 折板板幅变化时的腹板极限承载力

由表3可知，在sin α=d/a为定值且其他尺寸不变的条件下，当a/L≥0.069时，随着a减小，波纹增加、波纹变密，有限元模型计算得到的腹板极限承载力不断增大。但a/L≤0.069时，随着a减小，波纹增加，有限元模型计算得到的腹板极限承载力并不增大，反而有所减小。

4 材料强度分析

在有限元模型分析中，以钢材强度为变量，采用如图3所示的应力-应变关系及图4所示的有限元模型，其中平折板宽度a与斜折板宽度c均为66 mm，腹板高度330 mm，腹板厚度3 mm。其中，腹板弹性模量E为2.05×105MPa，泊松比μ为0.3。此时腹板的极限承载力Q为腹板钢材屈服强度 σy的函数，即 Q（σy）。

不同材料性能的腹板极限承载力见表4。

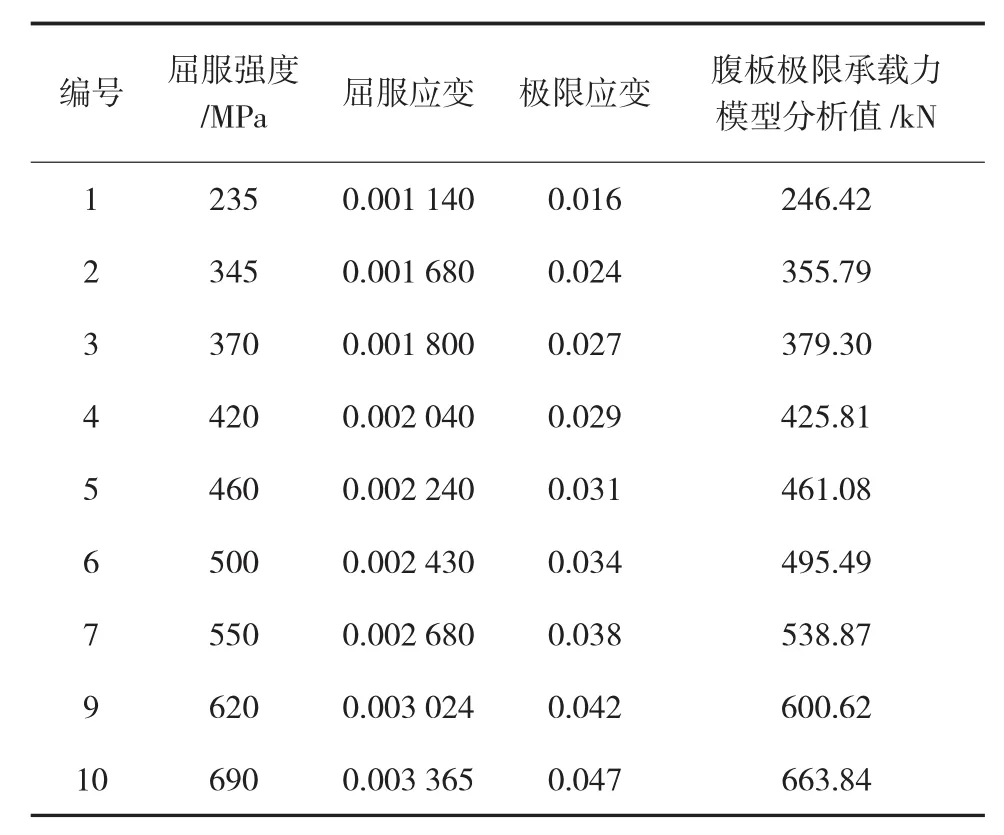
表4 不同材料性能的腹板极限承载力

由表4可知，在其他参数均保持不变的条件下，腹板的极限承载力随腹板屈服强度的增加而增加。本次计算结果的拟合曲线见图11。可以发现，腹板极限承载力Q与腹板屈服强度σy的关系为：

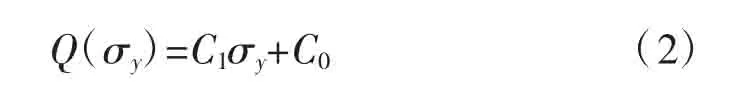
式中：C1、C0分别为调整系数。

5 结语

（1）波纹腹板H形钢梁的承载能力与腹板板厚有直接关系。在本次有限元分析中，承载能力与腹板板厚约为3次幂的关系。

（2）本次有限元建模时假设a=c，通过对比发现：当sin α≤0.61时，随倾角的增大，折板间侧向约束作用加强，腹板极限承载力逐渐增大；当sin α为0.61～0.71时，腹板极限承载力较高；当sin α＞0.71时，与 sin α=0.61～0.71 时相比，腹板的极限承载力变化不大且会增加腹板的材料用量。即d=0.61 a～0.71 a是综合材料用量与极限承载力的最佳值。

图11 不同屈服强度下腹板的极限承载力

（3）在倾角不变的条件下，当a/L≤0.069时，腹板的极限承载力随板幅a的增大而提高；当a/L≥0.069时，随着a的增大，波纹变稀，腹板的极限承载力反而减少。

（4）发现腹板的极限承载力与材料的屈服强度有一定相关性，拟合计算结果呈现线性关系。