钢桥面板横隔板多裂纹扩展三维数值模拟及其特性研究

金 通

（南昌市城市规划设计研究总院，江西 南昌 330038）

0 引言

正交异性钢桥面板自诞生以来，凭借其杰出的力学性能和较为出色的经济性，在现代化的桥梁建设中得到广泛应用[1]。然而由于在设计过程中的认识不足，以及该类桥梁对加工工艺要求较高，往往采用钢桥面板的桥梁在后期使用过程中会出现不同程度的疲劳开裂问题。根据国内外相关疲劳病害的统计结果可知[2]：钢桥面板中横隔板作为一个重要的构造部位，在实际工程结构中也存在着疲劳开裂问题的困扰。因此，针对正交异性钢桥面板中的疲劳开裂问题进行研究具有十分重要的实际工程意义。

目前而言，对于钢桥面板疲劳裂纹方面的研究主要集中在单一裂纹的数值模拟方面，但是针对工程中屡见不鲜的多裂纹现象，工程领域的研究学者还未有相关的研究成果。

本文在线弹性断裂力学理论的基础上，采用与有限元软件结合的方法，针对横隔板开孔处疲劳易损部位产生的多裂纹进行研究。基于对疲劳裂纹的三维扩展数值模拟，对裂纹前缘的应力强度因子K进行统计分析，可以得到横隔板弧形开孔处存在多条疲劳裂纹时的各条裂纹的扩展特性。

1 疲劳裂纹扩展关键理论基础

1.1 应力强度因子计算

经过国内外学者在断裂力学方面的不断研究和耕耘，发现应力强度因子是决定驱动裂纹扩展的一个重要因素，可以作为合理表征疲劳裂纹尖端区域应力场的一个参数。由于在实际工程结构中，疲劳开裂往往会以复合型开裂模式进行扩展，此时应以等效应力强度因子ΔKeff来对裂纹前缘的特性进行表征。本文中对应的复合型裂纹应力强度因子求解采用BS7910[3]所推荐的等效应力强度因子计算公式，即

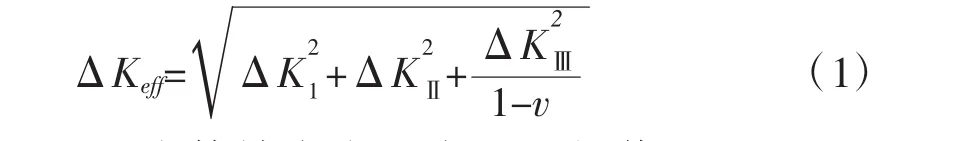
式中：ΔKeff为等效应力强度因子幅值；ΔKI,ΔKⅡ,ΔKⅢ分别为I型、Ⅱ型、Ⅲ型裂纹应力强度因子幅值；为材料泊松比。

1.2 疲劳裂纹扩展判据

国内外大量的针对材料中裂纹扩展速率与应力强度因子的关系的实验结果显示，在材料的da/dN-ΔK曲线图中有两条垂直的渐近线。其中左侧的渐近线位于ΔK=ΔKth处，ΔKth表示裂纹扩展的阈值，低于该值时，疲劳裂纹将不能进一步扩展。右侧的渐近线为Kmax=KC处，表示应力强度因子达到了使构件完全断裂的临界值。如果在双对数坐标中将da/dN表示为ΔK的函数，则该函数包含三个区间，分别为：门槛值区，Paris区，稳态撕裂的裂纹扩展区，如图1所示。

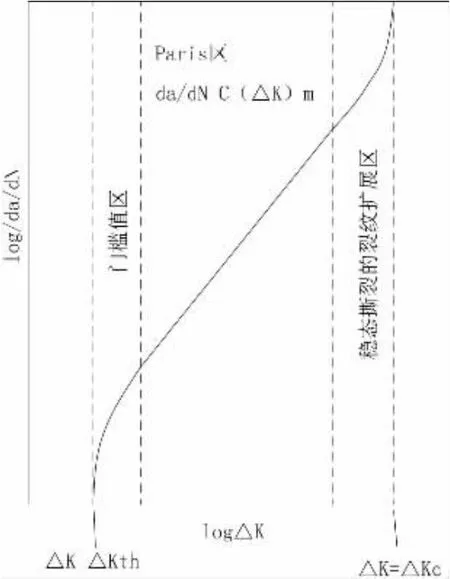
图1 裂纹扩展速率作为的函数的3个区

2 有限元模型建立

本文中以某斜拉桥正交异性钢桥面板为工程背景，该钢桥面板的构造具有在目前工程领域良好的代表性。其中，顶板板厚16 mm，横隔板板厚14 mm，横隔板间距2 500 mm，纵向U形加劲肋尺寸为300 mm×280 mm×8 mm，中心间距600 mm，钢材采用Q345qD。在该模型中，截取一个节间两个纵肋作为钢桥面板中横隔板处多裂纹扩展特性进行研究。结构模型的尺寸为：模型的总长度为2.7m，宽为1.4m，结构的高度为0.6m，具体的尺寸如图2所示。模型的加载区域有两处，每个加载区间均为200 mm×200 mm的正方形，结构所施加的荷载值为320 kN，加载方案如图2和图3所示。

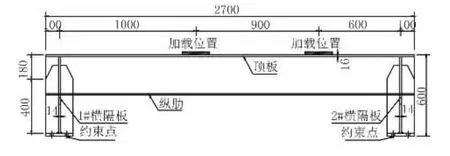
图2 加载模型方案立面示意图（单位：mm）

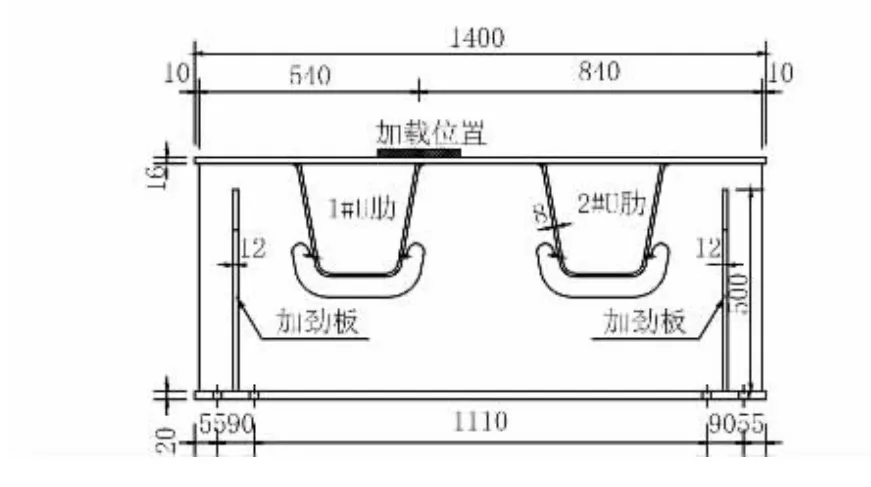
图3 加载模型方案横断面示意图（单位：mm）

本文采用通用有限元软件ANSYS建立结构模型对应的实体单元模型，于关注隔板的弧形切口处建立了两个初始角裂纹。在此基础上，对其进行裂纹扩展的数值模拟。在本模型当中，裂纹尖端采用的是能够较为精确反映尖端应力场奇异性的奇异单元Solid95，然后隔板的剩余部分采用的是单元Solid92。并且为了在保证计算精度的同时，也能够尽可能地提高有限元数值模型的计算效率，整体模型的其他部分均采用单元Solid45。根据国内学者刘益铭[5]对初始裂纹尺寸的选择，本文中的裂纹初始尺寸选择与其一致，两个初始角裂纹选取为1/4的扇形裂纹（半径为0.5 mm）。有限元数值模型以及初始裂纹的位置如图4所示。

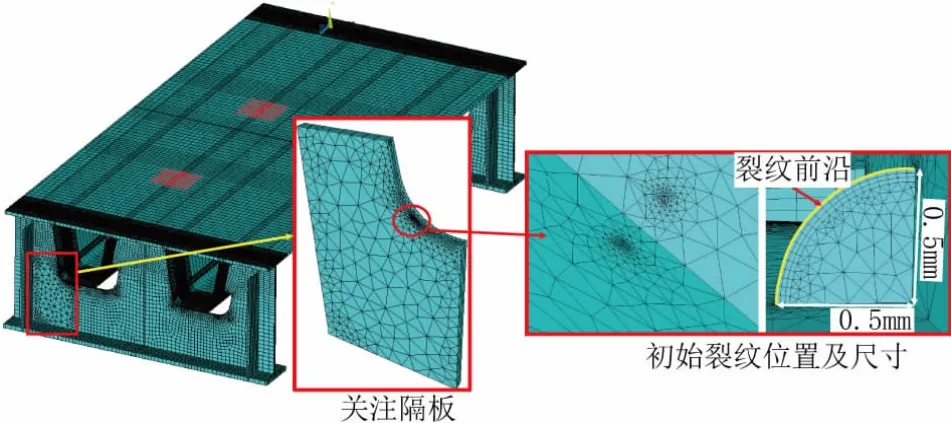
图4 有限元模型

3 疲劳裂纹扩展特性研究

横隔板处多疲劳裂纹扩展的三维数值模拟结果如图4所示，由于本论文的篇幅所限，并且裂纹扩展至当前55个扩展步长的情况下已经足以明显反应关注细节处多裂纹的扩展特性。因此，本文中裂纹扩展终止时的多裂纹形态如图5所示。

图5 裂纹形态示意图

钢桥面板中横隔板弧形开孔处产生的疲劳裂纹的原因主要是当荷载作用下横隔板的反复面外变形以及拉应力所致。根据前述过程中针对横隔板处多裂纹并存的数值扩展模拟，以及图4疲劳裂纹形态可知：（1）横隔板处角裂纹在一定的荷载循环次数作用后，将扩展成穿透型疲劳裂纹；（2）横隔板处即使是尺寸相同的初始裂纹，经过相同的荷载循环次数作用后，发展形态也不一样。

为了更为详细的研究横隔板处多裂纹的扩展特性，必须从裂纹前缘的应力强度因子幅值入手。由于疲劳裂纹前缘节点从理论上讲是无数多个点，在有限元数值模型中虽用有限多个点进行表示，但是对于进行分析研究来讲，对每个节点均进行统计分析显然是不可取的。因此，本文对每条裂纹的前缘均只取其两端节点进行分析，其相应位置如图6所示。

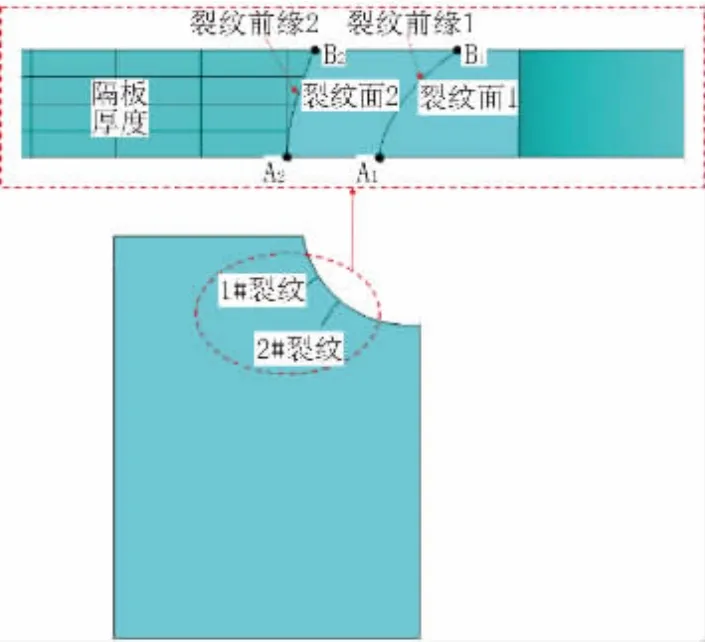
图6 裂纹前缘关注节点示意图

本文中裂纹尺寸长度选取表面外侧裂纹为控制长度，图7和图8中裂纹尺寸均以其为标准。通过对横隔板处多裂纹的扩展特性进行统计分析，如图7和图8所示。

根据图7和图8中的数据结果显示，可知：1#裂纹和2#裂纹关注节点的等效应力强度因子幅值ΔKeff当其处于初始裂纹阶段，其数值相差不大。但随着疲劳裂纹尺寸的增长，两条裂纹前缘的应力强度因子幅值会表现出完全不一样的趋势。1#裂纹前缘的应力强度因子幅值随着裂纹扩展至一定的尺寸后将会逐渐减小，并且最终其值会降低至裂纹扩展阈值之下，表明其最终会停止扩展。2#裂纹则在裂纹扩展一定尺寸后，将以较大的扩展速率一直扩展，并发展成一条主裂纹。

4 结论

通过对正交异性钢桥面板横隔板处多裂纹从初始角裂纹到穿透型裂纹的全过程数值模拟分析，采用线弹性断裂力学进行疲劳性能分析，得出以下结论：

（1）横隔板处角裂纹在一定的荷载循环次数作用后，将扩展成穿透型疲劳裂纹；

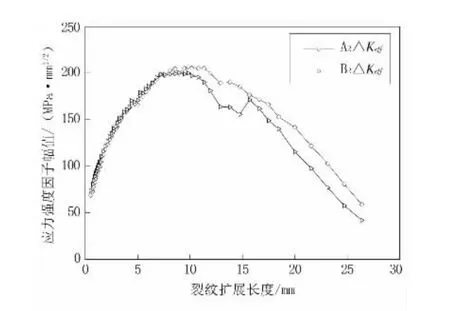
图7 1#裂纹等效应力强度因子幅值ΔKeff

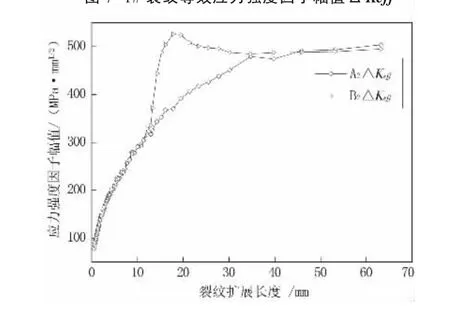
图8 2#裂纹等效应力强度因子幅值ΔKeff

（2）横隔板处即使是尺寸相同的初始裂纹，经过相同的荷载循环次数作用后，发展形态也不一样；

（3）1#裂纹前缘的应力强度因子幅值随着裂纹扩展至一定的尺寸后将会逐渐减小，并且最终其值会降低至裂纹扩展阈值之下，表明其最终会停止扩展。2#裂纹则在裂纹扩展一定尺寸后，将以较大的扩展速率一直扩展，并发展成一条主裂纹。