平均家庭户规模的模拟与预测—基于改进的Bi-logistic方法

焦桂花，傅崇辉，王玉霞

(1.广东医科大学 人文与管理学院，广东 东莞 523808；2.深圳市云天统计科学研究所，广东 深圳 518000)

一、引言

平均家庭规模是家庭人口分析、经济分析和环境影响分析的基础参数，家庭成员共享生活空间、能源、水、耐用消费品等形成家庭内部的规模效应[1]。平均家庭规模的变化会对资源节约和环境保护形成挑战，甚至对宏观经济也会产生影响[2-3]。

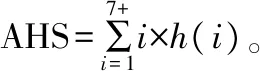
家庭内的人数是最基本的家庭人口学特征，平均家庭规模常用作描述家庭变化的指标，根据平均家庭规模的变化趋势，可以直观判断出家庭结构的变动趋势以及由此而引起的家庭需求的变动方向。比如，在人口老龄化的背景下，平均家庭规模下降可能伴随独居老年家庭比例和数量的上升，需要投入更多的居家养老支持资源；生育率下降会导致平均家庭规模缩小，同时也会导致家庭消费品(比如生活能源)的人均消费量增加，从而对环境产生负面影响。显然，平均家庭规模的变化对于家庭政策的制定和修订、社会实业部门的投资决策、环境保护和资源节约具有明确的指向意义。

虽然平均家庭规模的描述性统计分析和应用较为丰富，但受家庭数据的限制，鲜有直接对平均家庭规模进行模拟和预测的方法。本文将在前期研究的基础上，提出一种基于分段Bi-logistic曲线的平均家庭规模模拟和预测方法，并用中国省级家庭数据进行验证，以扩展现有平均家庭规模研究方法。考虑到中国不同地区处于家庭转变的不同阶段，因此首先对家庭转变阶段进行判断，再根据Bi-logistic曲线的参数意义，构建平均家庭规模模拟方程。从模型整体性、替代性和精确性三个方面对模型进行检验，并将研究结果用于模拟和预测中国典型地区的平均家庭规模变化。

二、文献回顾

随着人口和社会环境改变引起家庭结构的变化，家庭人口研究日益活跃，与平均家庭规模相关的家庭结构和家庭预测的理论研究和实证分析得到加强。

(一)基于家庭预测的平均家庭规模预测方法

家庭预测是常见的能够得到平均家庭规模模拟和预测结果的方法，经过简单的计算人口数量预测结果和家庭数量预测结果就可得到平均家庭规模的预测值[注]平均家庭规模预测值=人口数量预测值/家庭数量预测值。。

1.户主率家庭模型分别对不同年龄、性别和婚姻状态的人口中户主的比例进行预测，一般采用线性外推、回归模型或情景设定方法预测户主率，再结合人口预测结果得到家庭预测结果，根据家庭预测结果很容易得到平均家庭规模和家庭结构的预测信息。户主率法作为一种简单而稳健的家庭预测方法得到广泛应用，并衍生出一些扩展的户主率模型[4]。尽管户主率法对数据要求较低、简单易用，但它最大问题是很难通过预测(或假定)生育、死亡、结婚、离婚等人口参数来推测户主率的变动[5]。

2.微观仿真家庭模型对每一个样本所经历的生育、死亡、婚姻、家庭关系的状态变化进行模拟，汇总得出家庭人口的整体特征与分布[6]，同样可以得到平均家庭规模的预测结果。它的优点是可以精细地模拟研究个体或较小群体之间的异质性差异及其概率分布，在家庭生命周期研究中有明显的优势。但其缺点是预测起点的样本人口规模与抽样比必须足够大，而人口普查所搜集的家庭人口信息无法满足微观仿真模型对家庭人口特征分类很细的需求，因此限制了其应用范围。

3.宏观动态家庭模型将起始人口按家庭状态分为不同的类型，运用状态转移概率矩阵估计下一时点的家庭状态，从而得到整个人口的家庭状态变化。以LIPRO模型为代表的宏观模拟家庭户预测模型需要不同家庭户类型之间相互转换的转移概率数据[7]，常规的人口统计、普查与调查很难满足这些特别的数据要求，必须通过专门设计的家庭户调查才能获得。

ProFamy模型将人口按八个状态分类，状态转移概念矩阵包括性别、年龄别死亡率、初婚率、胎次别生育率、迁移率、离家率、离婚率、离婚再婚率、丧偶再婚率。虽然上述状态转移概率数据可以通过常规人口数据源获得，但通常需要多个人口数据来源才能满足要求。Yi等在运用ProFamy预测美国家庭变化时，由于缺乏离家率的数据，只能采用设定的方法[8]。

(二)基于家庭结构预测的平均家庭规模模拟和预测方法

除了可以间接模拟和预测平均家庭规模外，家庭结构模型的家庭规模结构还可以通过加权平均的方法得到平均家庭规模的预测结果。

Ironmonger等运用家庭规模倾向率(household size propensity)预测澳大利亚的家庭规模结构的变化[9]，但基于两期人口普查数据(1981、1986)得到的预测参数(家庭规模倾向率)很难反映未来的变化趋势。另外还有家庭成员率、家庭状态率、家庭关系率的方法可以预测家庭数量和结构[5]。这类方法比家庭预测模型所需要的数据和参数更少，也相对简单，但模型参数的预测需要较长的时间序列数据，在不满足数据要求时，往往只能假设最近的参数在预测期内保持不变。

总体上看，现有能够模拟或预测平均家庭规模的方法多为间接方法，即通过人口和家庭预测或家庭结构预测间接得到平均家庭规模，所涉及的数据和参数较多，许多发展中国家或小区域无法满足。本文利用常规的人口数量和家庭数量指标，采用改进Bi-logistic曲线拟合平均家庭规模的变化趋势，根据平均家庭规模时间序列数据拟合曲线参数，避免对家庭数据的过高要求。这种直接拟合平均家庭规模的方法完全独立于家庭预测模型或家庭结构模型，可以与家庭预测结果或家庭结构预测结果相互检验。

三、研究设计

(一)概念界定

家庭规模是指家庭成员人数，全社会平均的家庭人数即为平均家庭规模。国际上通常按照共同生活(housekeeping)和共同居住(dwelling unit)的标准界定家庭成员[10]。按照“共同生活”的标准，家庭内部共享食物等生存资料的成员被视为家庭成员；按照“共同居住”的标准，居住在同一建筑单元里的人被视为家庭成员。

中国人口普查对家庭户的定义为：以家庭成员关系为主，居住一处共同生活的人口，作为一个家庭户[11]。可见，中国对家庭户的界定需要同时满足共同生活和共同居住两个标准，本文的“家庭”也采用这个标准，平均家庭规模是指排除了集体户人口的家庭户人口的家庭规模，即平均家庭户规模。

(二)数据选择

人口普查是能够获得准确家庭户数据的方式之一，但它不能提供时间序列数据，中国每10年才进行一次人口普查。为了获得时间序列的省级家庭规模数据，采取1955—2014年人口数量和家庭数量计算相应年份各省、市、自治区的家庭规模[注]平均家庭规模=人口数量/家庭数量。。1991年以前，中国的人口数量和家庭数量来自公安户籍统计资料，但没有区分家庭户和集体户人口；1992年以后中国开始进行人口变动抽样调查，抽样比例约为1‰。同样，人口变动抽样调查公布的结果也没有区分家庭户和集体户人口。虽然家庭户人口占绝大部分[注]2010年第六次人口普查显示，家庭户人口占总人口的比例为90.81%。，但本文采用的计算方法会高估平均家庭规模[注]由于人口数量大于家庭户人口数量，通过人口数量和家庭数量计算的平均家庭规模大于本文定义的平均家庭规模。，在随后的模型检验和预测时，需要用人口普查口径的家庭规模进行校正。

1955—1994年各年人口数量和家庭数量引自《中国人口统计年鉴(1995)》，1995—2005年各年人口数量和家庭数量引自各年《中国人口统计年鉴》，2006—2014年各年平均家庭规模和家庭户数量引自各年《中国人口与就业统计年鉴》。

(三)Bi-logistic曲线

按照Meyer的定义[12]，Bi-logistic曲线可以表示为：

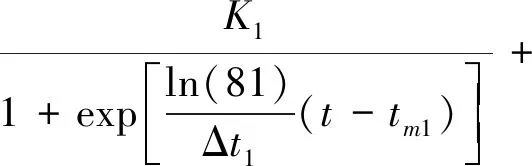
(1)

上升-下降曲线可以表示为两个logistic曲线之和(a、b)，采用时间序列数据可以估计式(1)的参数，如图1所示。

图1 Bi-logistic曲线示意图

参数估计的标准过程是假设时间序列数据的测量误差是独立、正态分布、同方差。离差(Residuals)定义为时间时间序列数据的观测值(ti，yi)与Bi-logistic曲线的拟合值(N(ti))之差：

Residuals=N(ti)-yii=1，2，…，m

(2)

运用非线性回归方法使得离差平方和最小(见式(3))就可以估计出Bi-logistic曲线的最优参数。

(3)

(四)研究方法

家庭结构变化的收敛理论认为，伴随着城市化、工业化和人口转变，家庭结构趋向于核心化，家庭规模小型化[13]。根据发达国家实证经验，在家庭结构变化过程中，平均家庭规模表现为如图2所示的3个阶段：第1阶段家庭规模呈轻微扩张趋势；第2阶段家庭规模快速收缩；第3阶段家庭规模慢速收缩，并围绕2～3人/户波动[14]。本文将这种规律性的变化过程称为家庭转变，如图2所示。

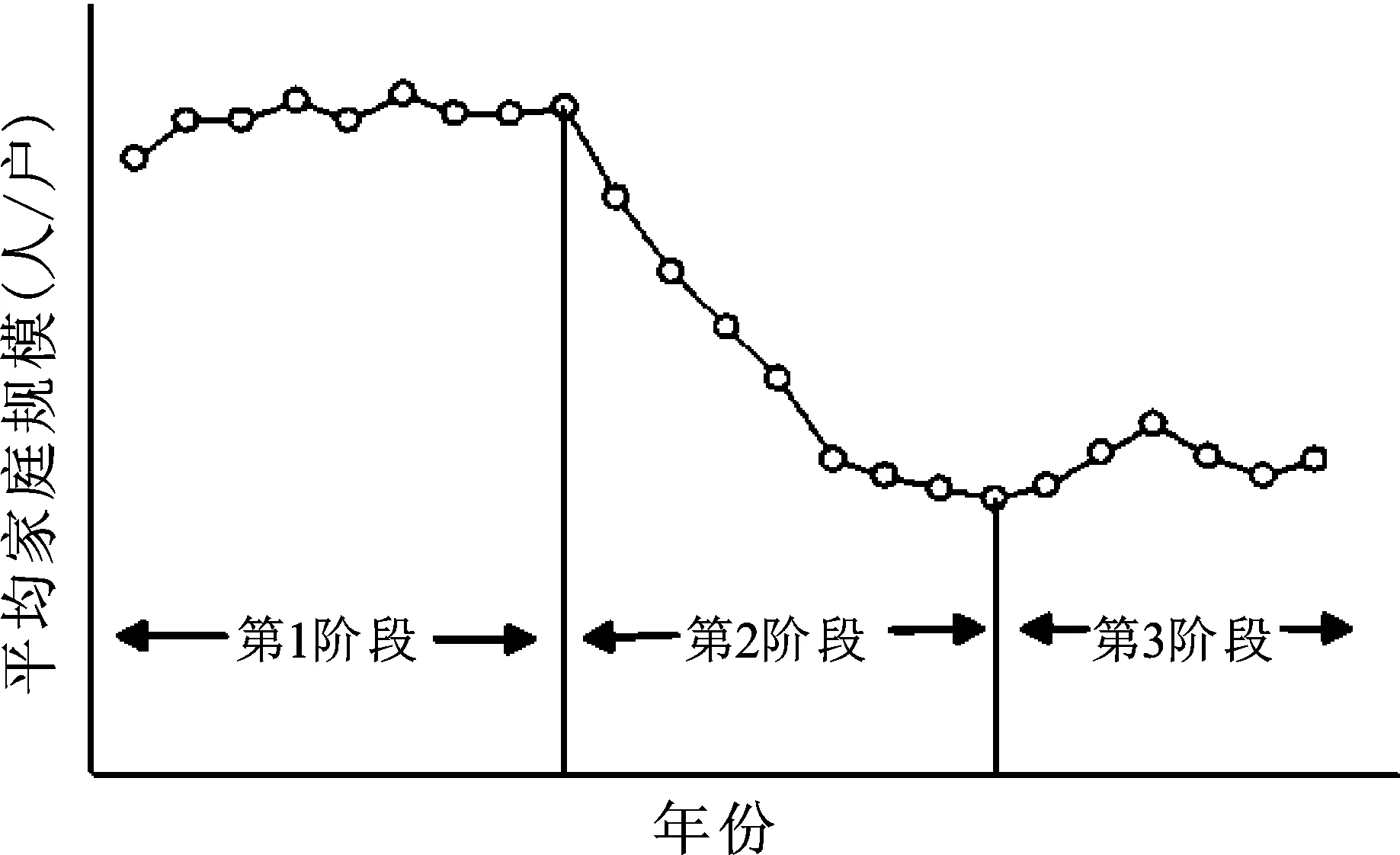
图2 家庭转变过程示意图

中国的家庭转变已经跨越了第1阶段(转折点在1974年左右)，接近第2阶段的末期。由于中国所有地区已经渡过了家庭转变的第1阶段，本文只考虑家庭转变第2阶段以后的情况，如图3所示。

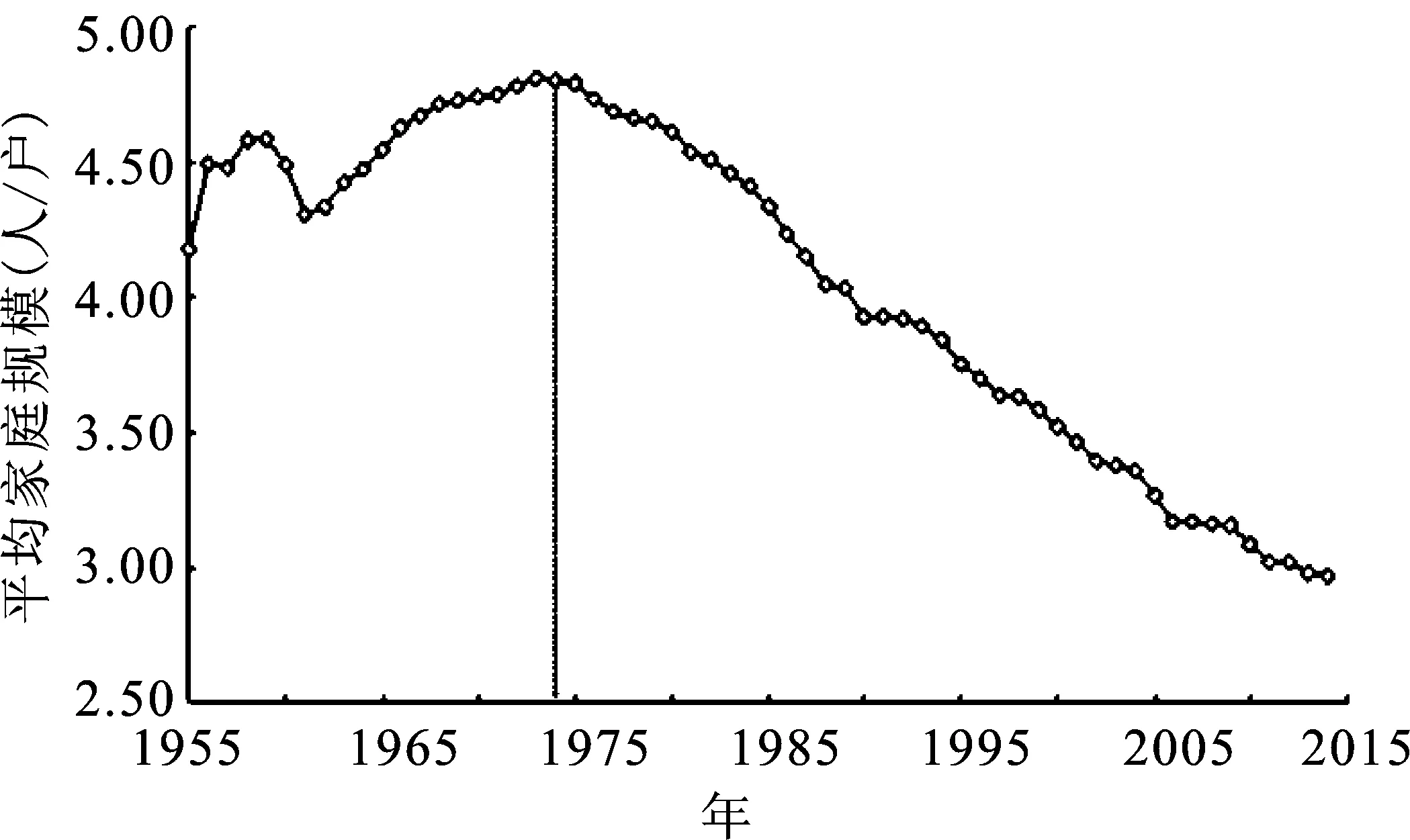
图3 中国平均家庭户规模动态变化趋势图

1.家庭转变阶段判断准则

(1)判断第2阶段的起始点。为了排除平均家庭户规模的随机波动，将第2阶段起始点设置为家庭规模首次连续下降的时点，用公式表示为：

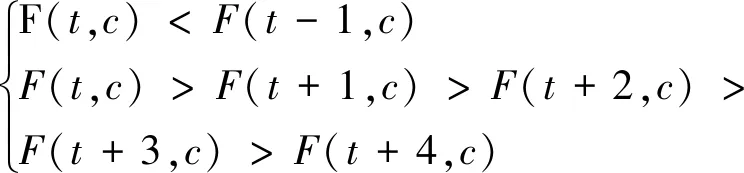
(4)

其中，F为平均家庭户规模，t为年份，c为地区。根据式(4)的含义，第2阶段起始点的判断准则为：平均家庭户规模首次出现至少连续5年下降的时点。

(2)判断第3阶段的起始点。根据家庭转变理论，将第3阶段起始点设置为平均家庭户规模首次出现低位波动的时点，用公式表示为：

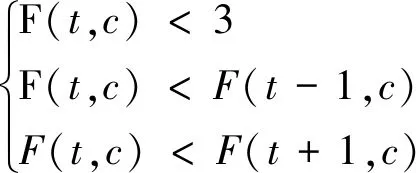
(5)

根据式(5)的含义，第3阶段起始点的判断准则为：平均家庭户规模小于3人/户，且首次出现上升的时点。

根据上述判断准则，满足式(4)条件、不满足式(5)条件的地区可以判断为处于家庭转变第2阶段；满足式(5)条件的地区可以判断为处于家庭转变第3阶段，只有北京、上海、天津和浙江进入了第3阶段。前者表现为平均家庭户规模持续下降，可采用Bi-logistic曲线进行模拟和预测[12]；后者表现为平均家庭户规模围绕某一固定值波动，可采用自回归模型进行模拟和预测。

2.平均家庭户规模模拟方程

发展中国家的平均家庭户规模普遍大于3人/户[15]，还没有进入家庭转变第3阶段，中国也只有少数地区刚刚进入家庭转变第3阶段，但数据点太少，还不支持自回归模型的拟合条件，因此本文只对家庭转变第2阶段的平均家庭户规模进行模拟。

如图3所示，中国的平均家庭户规模表现为典型的S型曲线，Logistic函数常用于模拟具有一定承载容量的系统，也包括人口生态系统[16]。当社会环境改变导致系统的承载容量发生变化时，分别控制两条logistic曲线的参数进行叠加，可以拟合承载容量变化的复杂系统[12]。Bi-logistic曲线既可以拟合增长过程，也可以拟合下降过程。

观察图3所示的平均家庭户规模变化过程(第2阶段)可知，中国平均家庭户规模经历了早期的快速下降阶段和后期的慢速下降阶段，可以采用Bi-logistic函数模拟整个过程的不同下降速率[12，16]。每年平均家庭户规模下降幅度(以下称为平均家庭户规模减量，用ΔF表示)用平均家庭户规模的函数表示为：

ΔF(t，c)=F(t，c)-F(t+1，c)=f(F(t，c))

(6)

中国各省、市、自治区的平均家庭户规模减量函数的观测曲线大致可以分为单峰和双峰两种类型。图4a可以理解为平均家庭户规模经历了快速下降和慢速下降两个过程，图4b显然是受到某种人口事件的干扰。

20世纪90年代，中国出现流动人口快速增长的现象[17]，1990—1995年流动人口的年均增长率达到27.07%。由于人口流动，总有部分家庭成员未共同居住[18]，人口流动或多或少会导致平均家庭户规模下降。

图4中，a点对应的年份为1994年，b点对应的年份为1995年，正值中国人口流动高涨之时。如图4a和4b所示。

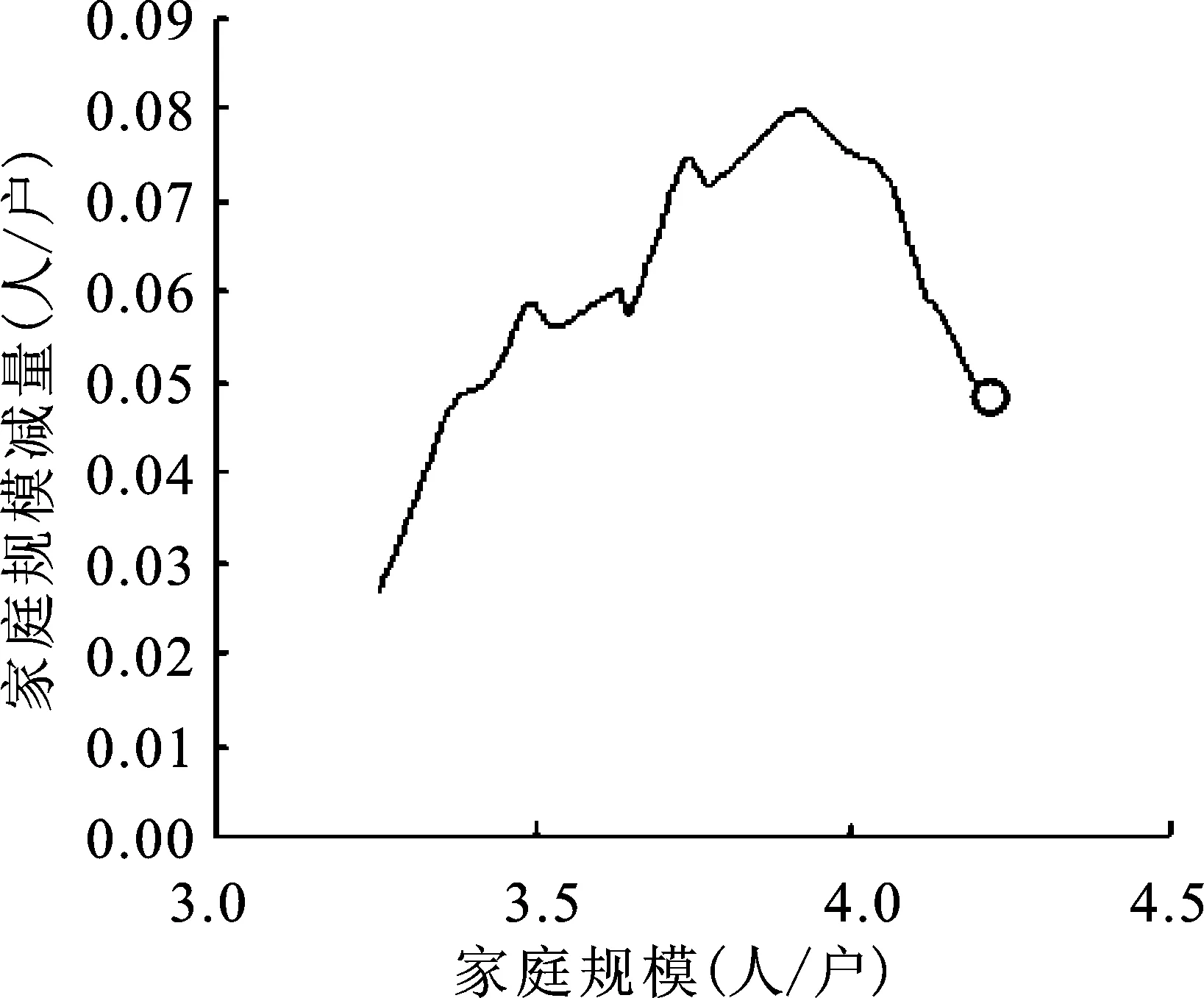
图4a 江西省家庭规模减量观测曲线图

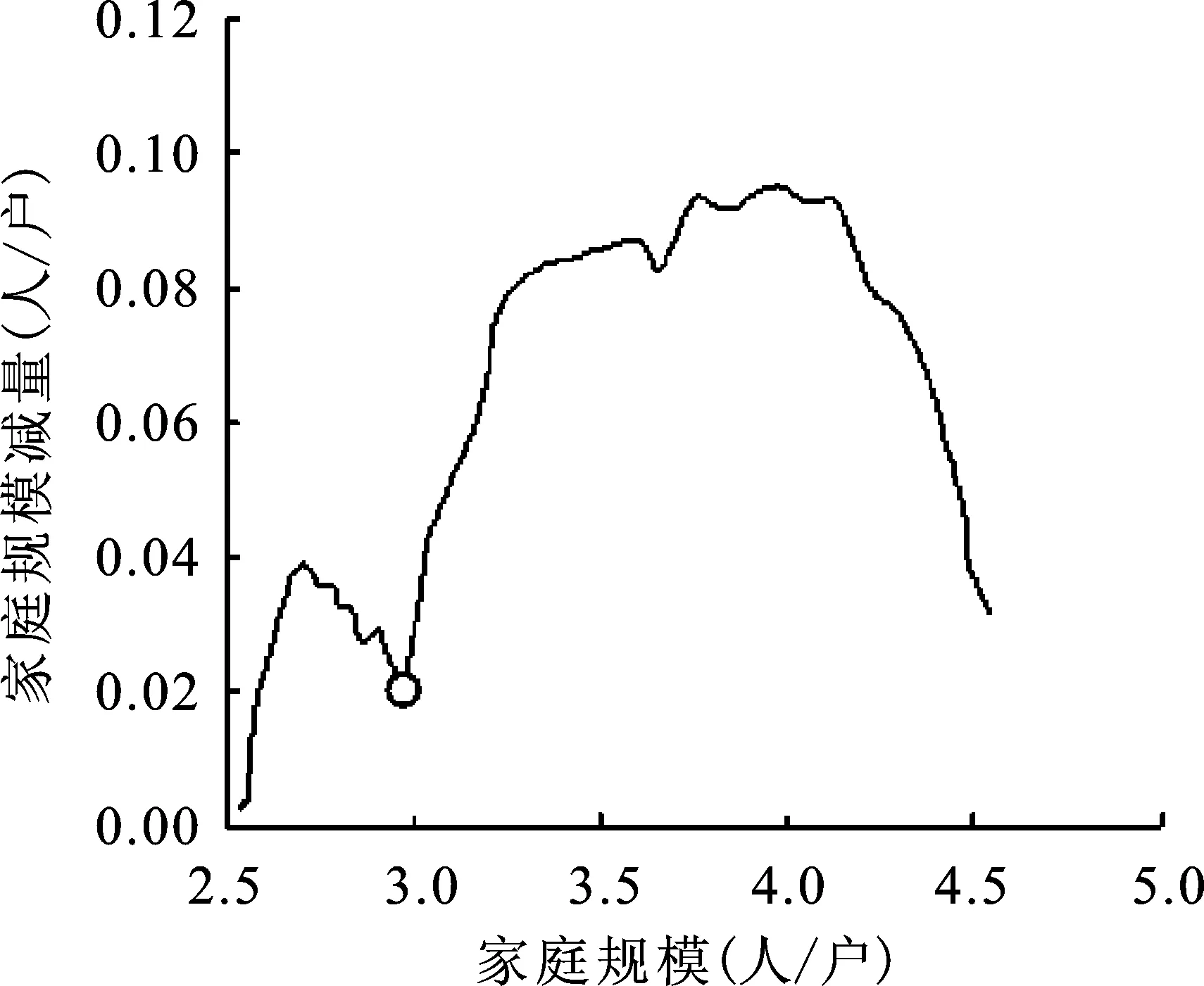
图4b 北京市家庭规模减量观测曲线图

当流动人口加速期正好与平均家庭户规模减量的上升期重叠时(a点)，就表现为单峰形状；当流动人口加速期与平均家庭户规模减量的下降期重叠时(b点)，就表现为双峰形状。前者称为Ⅰ类地区；后者称为Ⅱ类地区。

Ⅰ类地区采用Bi-logistic曲线拟合，即：

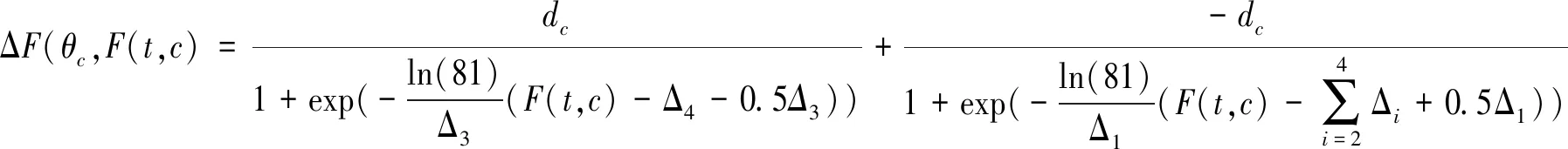
(7)

式中，θc= (Δ1，Δ2，Δ3，Δ4，dc)，为5个待估参数。

Ⅱ类地区采用分段Bi-logistic曲线拟合，即

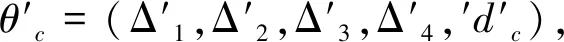
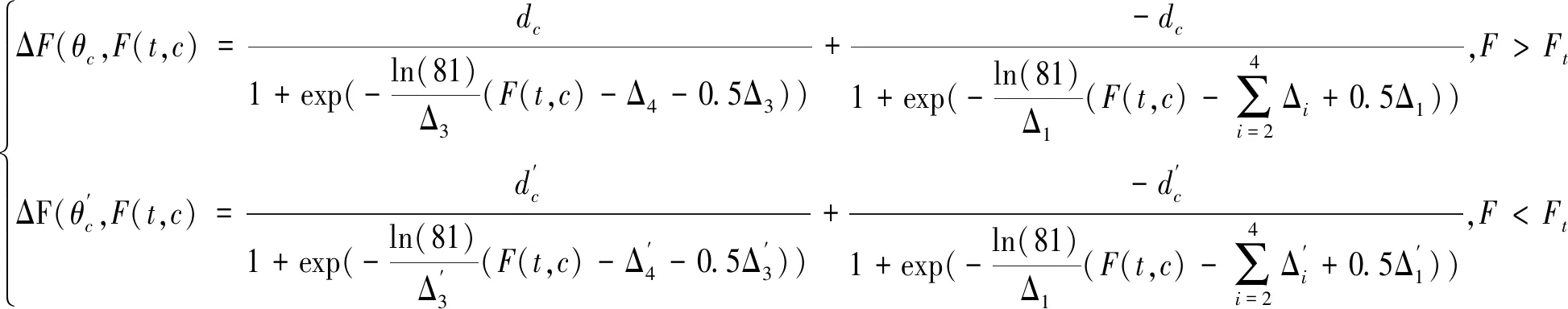
(8)

将式(7)或式(8)的结果代入式(6)，可得：

F(t+1，c)=F(t，c) - ΔF(t，c)

(9)

3.参数意义

采取L-M非线性最小二乘法估计式(7～8)的参数，需要事先给定待估参数的初始值。了解各参数的意义不仅有助于通过观测曲线估计参数的初始值，而且能够根据参数意义判断拟合值的合理性，以及根据参数意义设定预测参数，见图5所示。

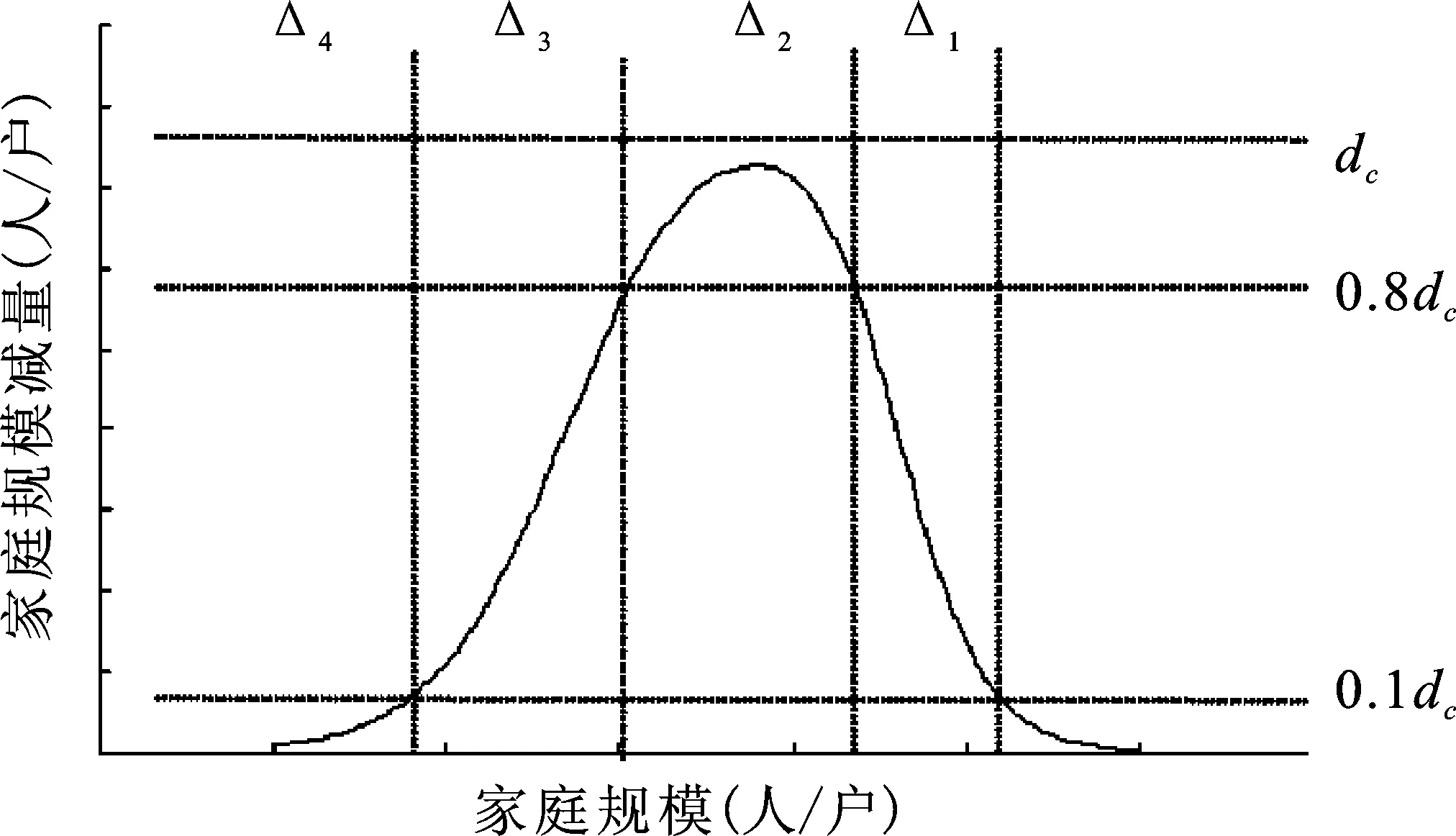
图5 家庭规模模拟方程的参数意义图

如图5所示，dc为平均家庭户规模减量可能达到的峰值；Δ1为平均家庭户规模减量快速上升阶段；Δ2为平均家庭户规模减量高位转折阶段；Δ3为平均家庭户规模减量快速下降阶段；Δ4为平均家庭户规模减量低速下降阶段。

四、结果分析

(一)模型检验

1.整体性检验

平均家庭户规模模拟方程采用非线性最小二乘法进行拟合，可以从决定系数和整体性检验判定模拟方程的稳健性。表1显示，平均家庭户规模模拟方程的解释力度普遍较高，R2在78%～98%之间，F检验也支持模拟方程有显著性意义，基于历史数据的模拟方程是稳健的，结果详见表1。

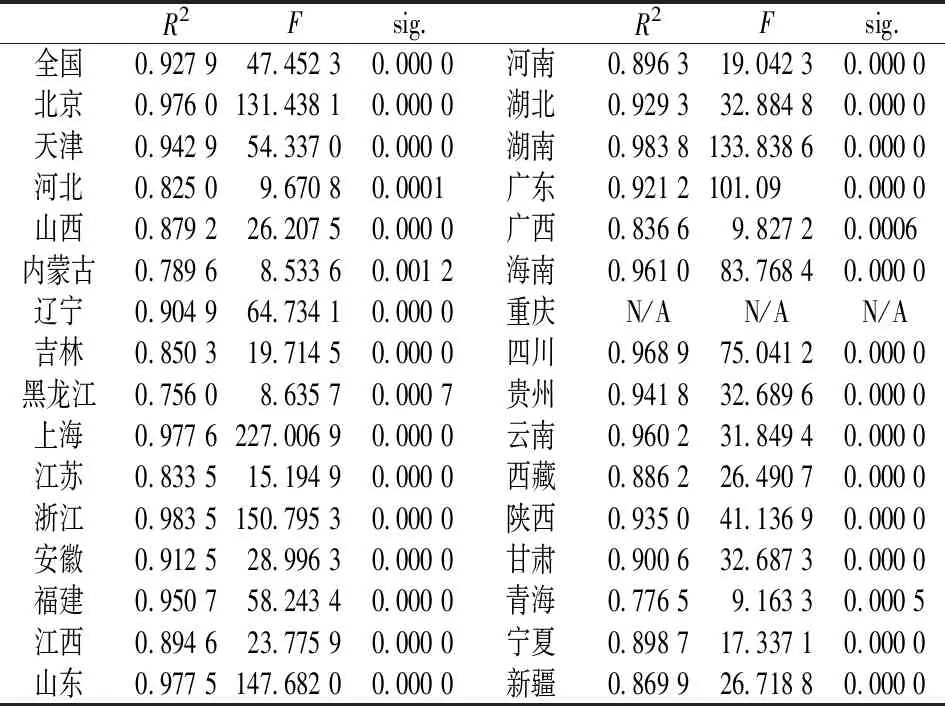
表1 拟合优度检验

注：数据来源于模型计算结果。

2.替代性检验

重庆市是1994年从四川省分离出来的直辖市，它的平均家庭户规模变化规律应该与四川省高度相似。用四川省的模拟方程参数估计重庆市的平均家庭户规模，如果拟合值能够达到精度要求，则说明平均家庭户规模模拟方程具有良好的替代性。

中国于1990年、2000年和2010年分别进行了3次人口普查，可以得到相应年份家庭规模的准确数据[注]人口普查得到的家庭规模是家庭户人口数量/家庭户数量。。以1990年重庆市的平均家庭户规模(3.56人/户)为基点，代入四川省的平均家庭户规模模拟方程，估计2000年和2010年重庆市的平均家庭户规模，并将估计值与实际值(人口普查得到的数值)相比较。结果显示，2000年和2010年重庆市的平均家庭户规模的估计值分别为3.33人/户和2.86人/户，与实际值的误差分别只有3.85%和3.09%[注]人口普查数据显示，2000年和2010年重庆家庭规模分别为3.21人/户和2.77人/户。。替代性检验说明，当无法获得小区域家庭数据时，可以用大区域的模型参数代替，或者用类似地区的参数进行替代。因此，平均家庭户规模模拟方程可以起到类似于模型生命表的作用。

3.准确性检验

根据平均家庭户规模模拟方程的特点，选择具有代表性的几个地区进行准确性的事后检验。它们分别是模型解释力最高的北京市和最低的黑龙江省，以及同样是分段Bi-logistic的全国；模拟方程为Bi-logistic的上海市和山东省。

以1990年人口普查的平均家庭户规模为基点，将模型参数代入式(4～6)，得到2000年和2010年的平均家庭户规模估计值，并与对应年份的实际值进行对比。从表2结果可以看出，2000年的估计误差在5%以内，2010年的估计误差在10%以内。相对来说，分段Bi-logistic模型的估计精度好于Bi-logistic模型。总之，采用本文的模拟方程估计家庭规模，10年期的估计误差小于5%，20年期的估计误差小于10%，模型的精度较好，数据详见表2。

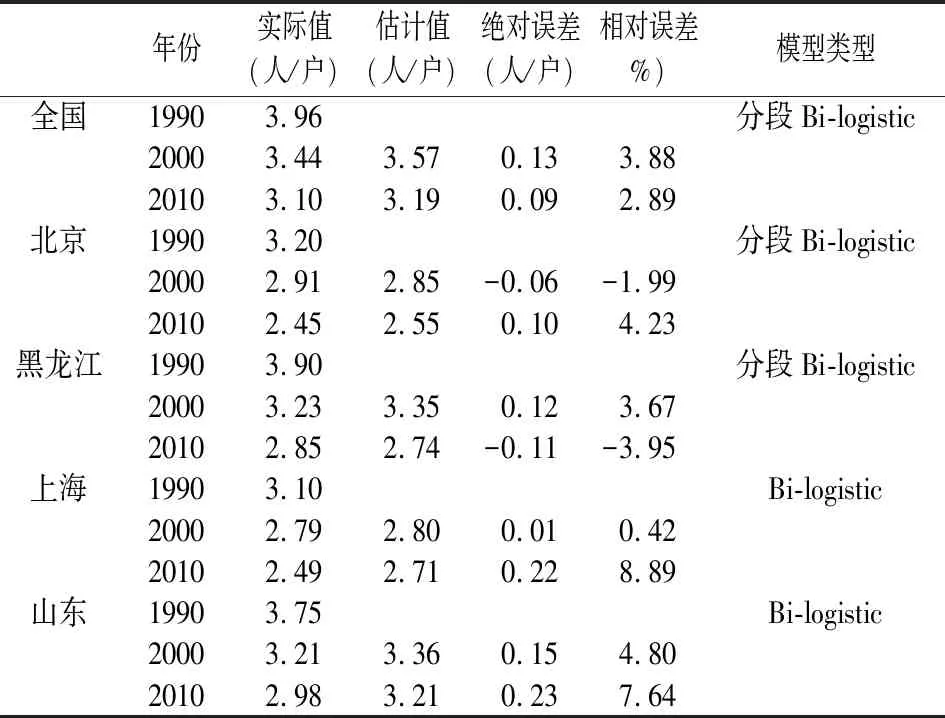
表2 模型事后检验

注：实际值引自对应年份各地区的人口普查公报。

(二)拟合结果

表3为中国各省、市、自治区的平均家庭户规模模拟方程参数的拟合结果。其中，山西省、辽宁省、上海市、江西省、山东省、湖南省、广东省、山西省、西藏自治区和新疆自治区是Bi-logistic方程，其余地区为分段Bi-logistic方程。

从拟合结果看，20世纪90年代的人口流动对中国的平均家庭户规模变化产生了深刻影响，分段Bi-logistic方程反映了这种典型人口事件在平均家庭户规模变化上的表现。对于平均家庭户规模模拟方程为Bi-logistic的地区也不是没有受到人口流动的影响，只是这些地区的人口流动加速期与平均家庭户规模减量的上升期重叠，从而表现为单峰图形，数据如表3所示。

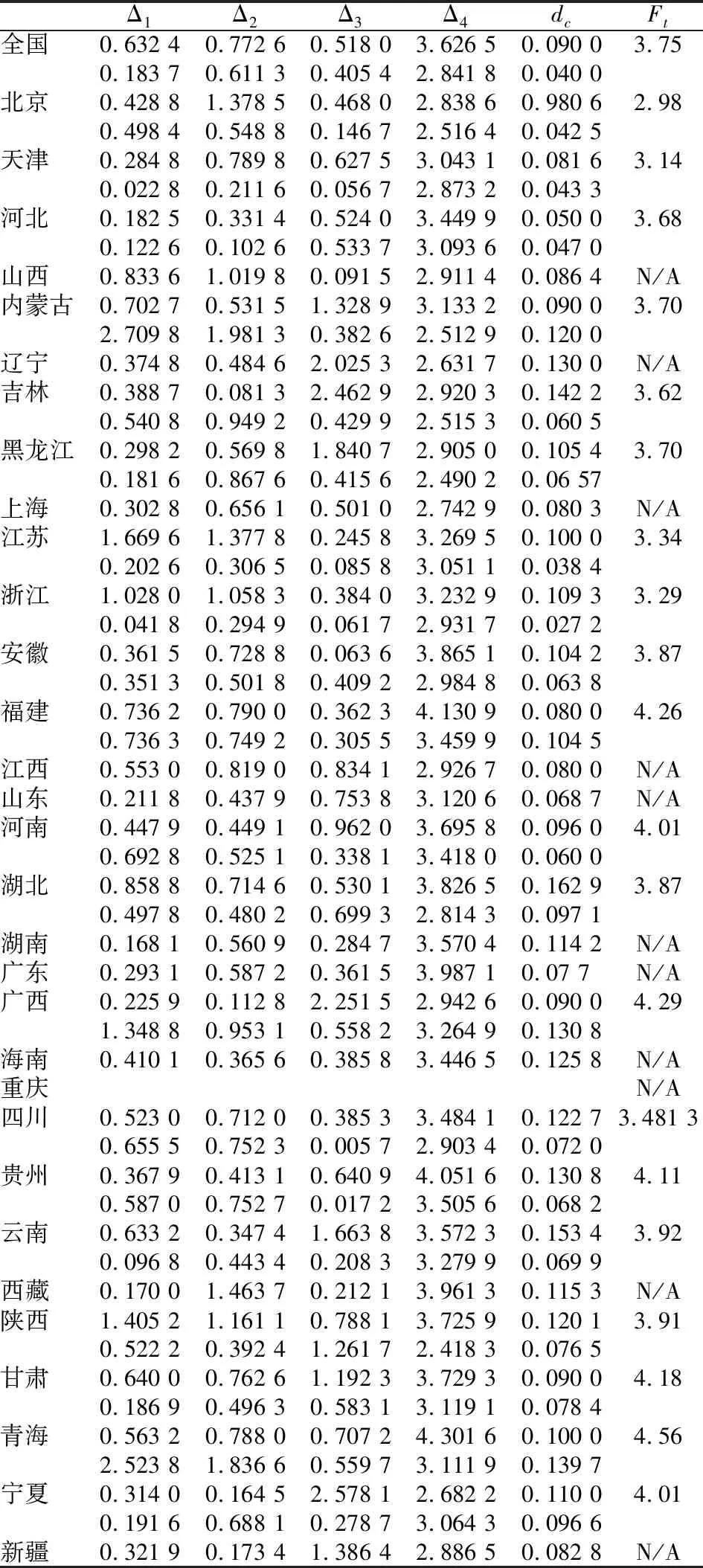
表3 平均家庭户规模模拟方程的参数拟合值

注：重庆的参数没有拟合，本文用四川的参数替代。

实际应用过程中，给定起始年份的平均家庭户规模，将表3的参数值代入式(7)或式(8)得到平均家庭户规模减量的估计值，再由式(9)计算下一年份的平均家庭户规模估计值，依此类推可以得出未来各年份的估计值。对于分段Bi-logistic的地区，在分界点(Ft)前后分别采用不同的参数值。

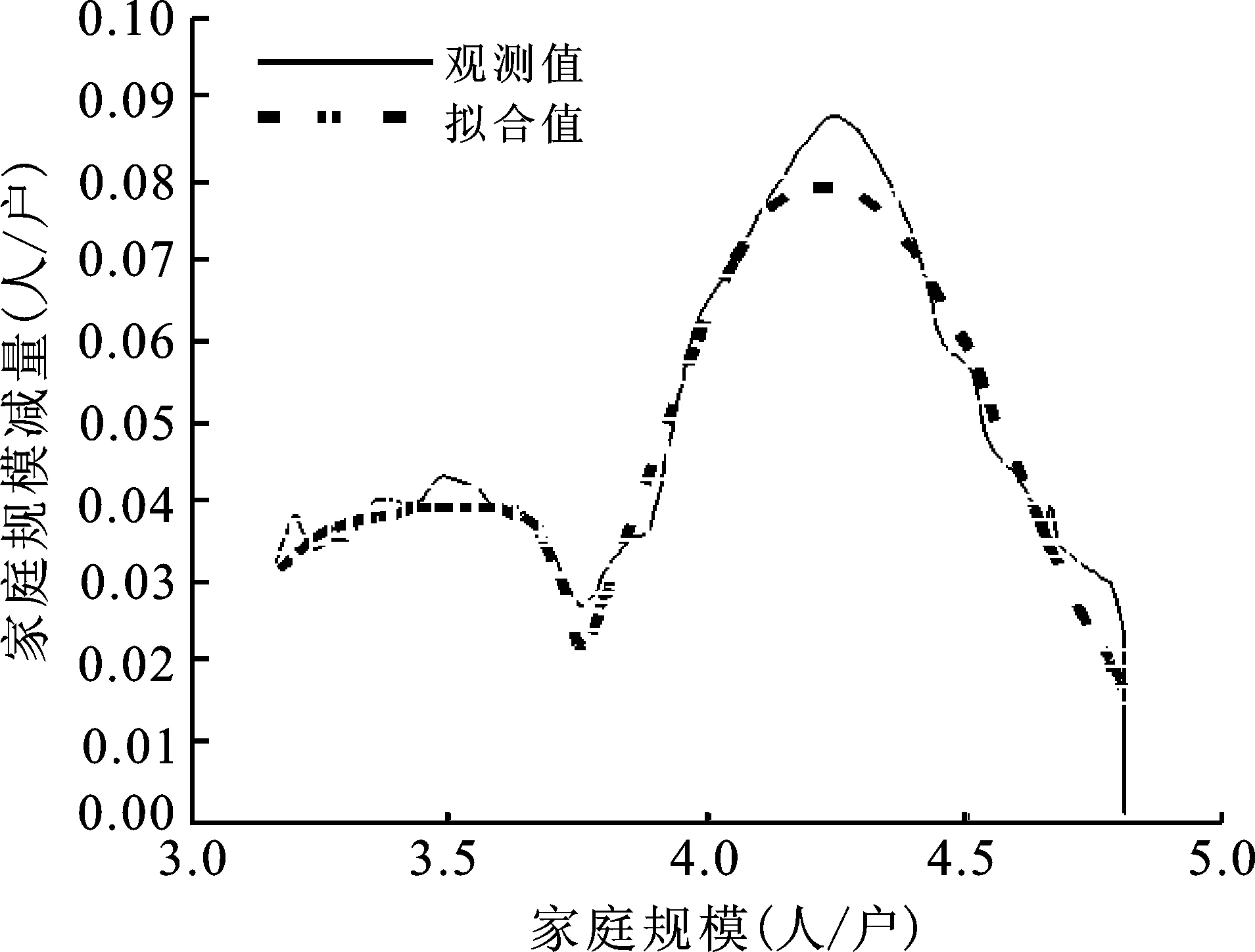
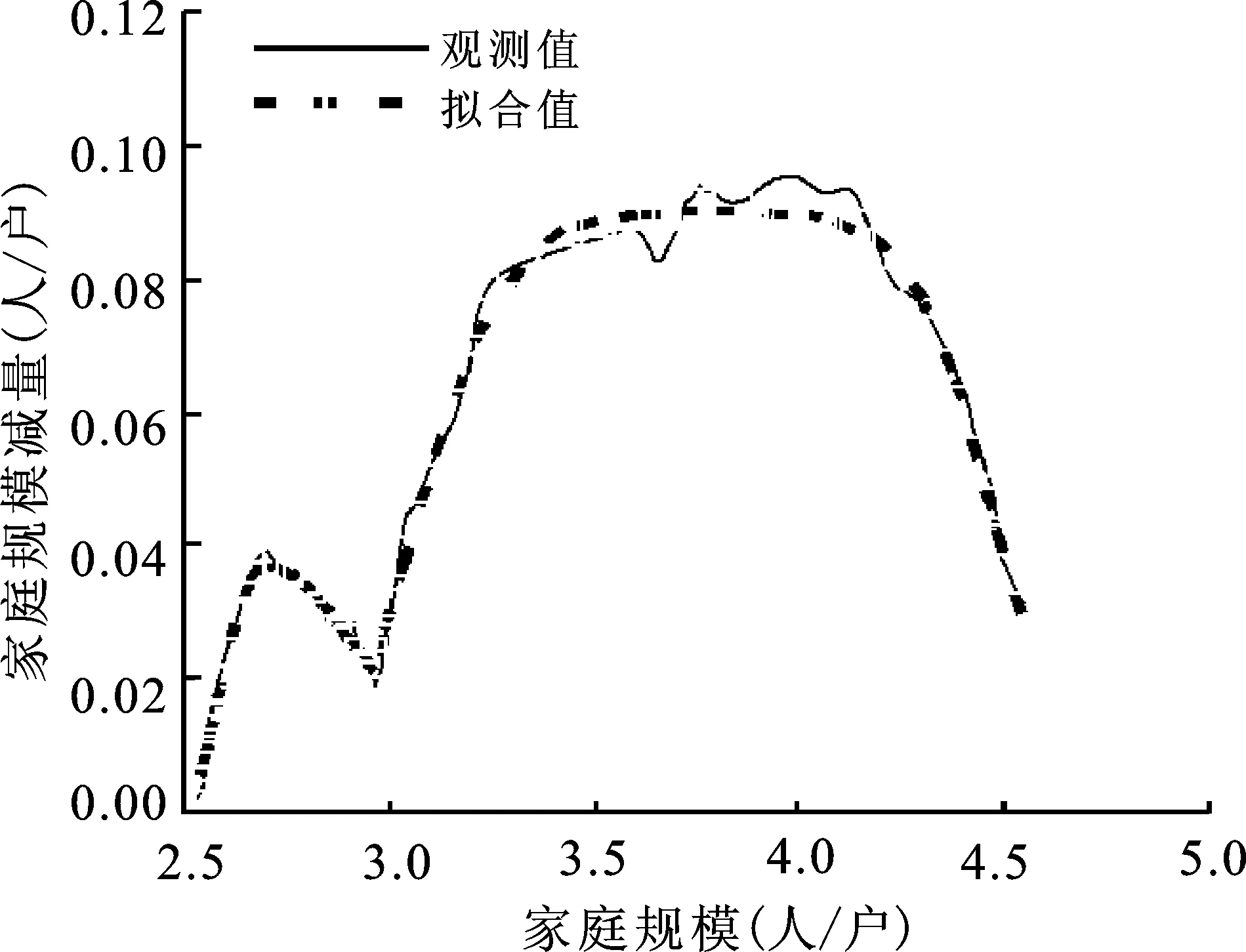
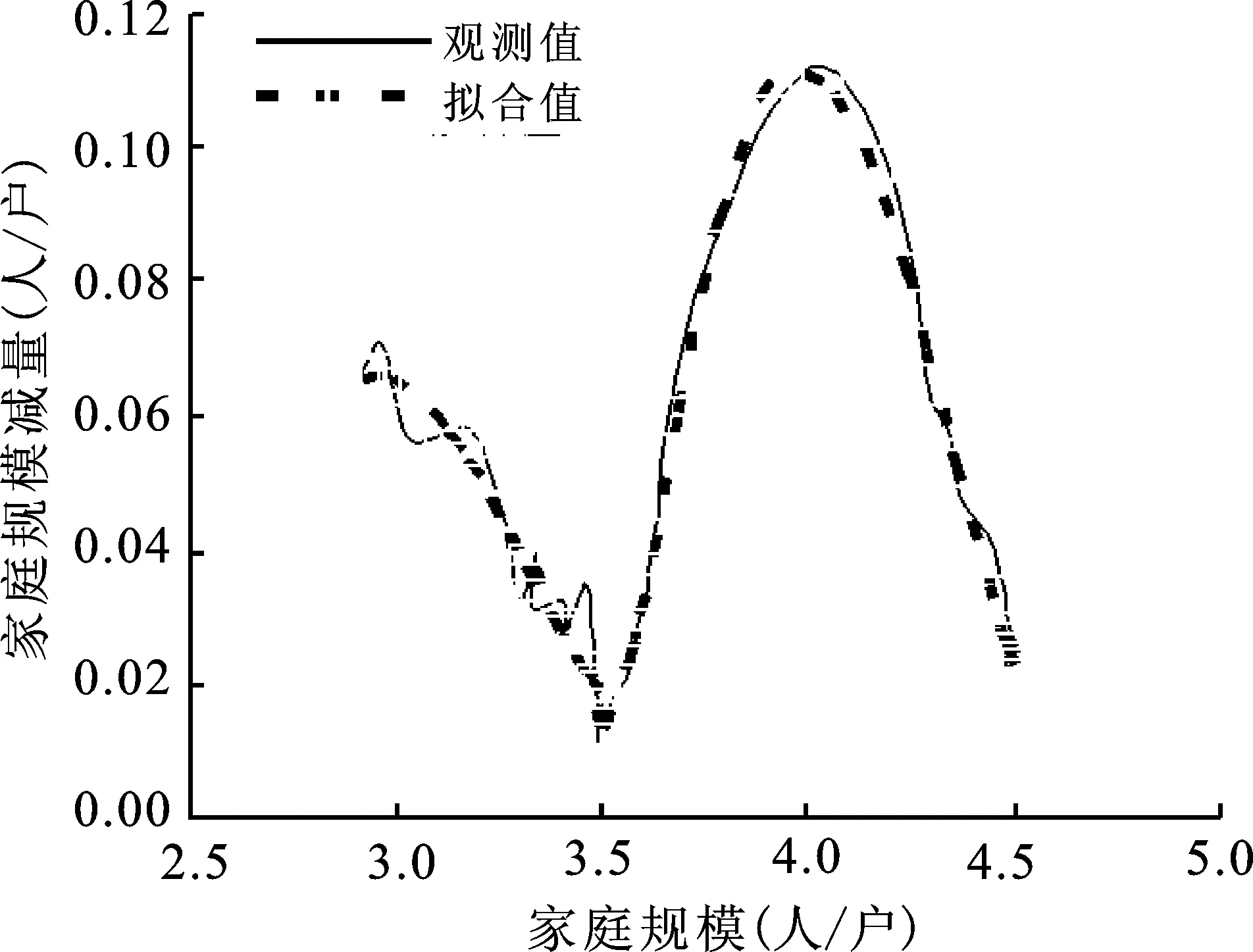
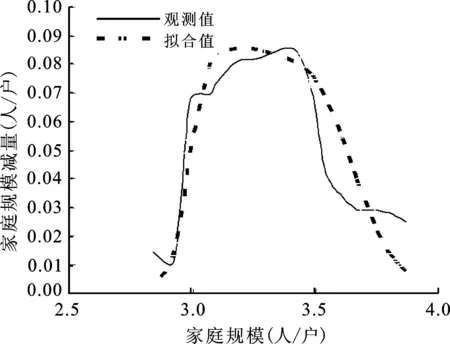
图6a 全国图6b 北京市图6c 四川省图6d 山西省图6 平均家庭户规模减量拟合曲线图

图6a～d分别给出了全国、北京市、四川省和山西省的平均家庭户规模拟合图形。平均家庭户规模的拟合有两方面的用途：一是用于模拟没有家庭数据的地区的平均家庭户规模变化过程；二是用于校正平均家庭户规模观测值。利用人口普查时点的平均家庭户规模数值校正平均家庭户规模模拟方程取得的估计值，其误差在可以接受的范围。

(三)预测结果

平均家庭户规模模拟方程不仅可以用于模拟平均家庭户规模变化的历史过程，也可以预测未来平均家庭户规模变化的趋势。

从历史看，西方发达国家的平均家庭户规模经历了快速下降阶段后，在2～3人/户时从慢速下降过渡到低位波动阶段[5]，也就是进入家庭转变的第3阶段。从现实看，中国的北京、上海等地区也是在3人/户左右进入平均家庭户规模减量慢速下降阶段，并逐步过渡到家庭转变第3阶段。因此，对应于平均家庭户规模模拟方程Δ4的参数意义，假设中国各省市自治区的平均家庭户规模达到3人/户后进入慢速下降阶段，预测未来中国各省、市、自治区的平均家庭户规模变化趋势。本文以全国、北京市、上海市、重庆市、黑龙江省和山东省为例，以2010年第六次人口普查的平均家庭户规模为基点，预测2010—2030年平均家庭户规模的变化，如图7所示。

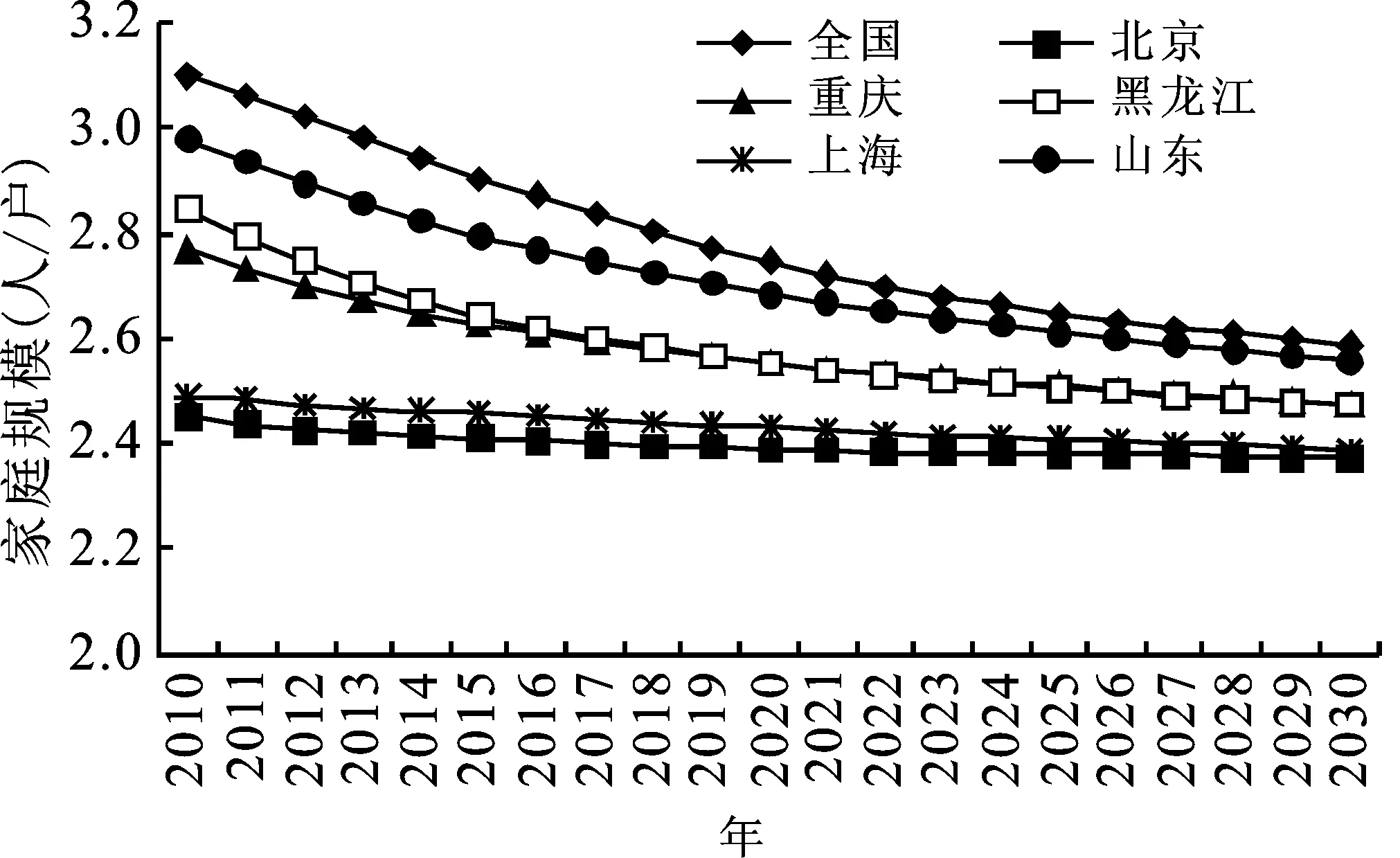
图7 平均家庭户规模预测结果图

从图7的预测结果看，起始平均家庭户规模水平较高的全国和山东省下降速度较快，分别从2010年的3.10人/户和2.98人/户，下降到2020年的2.75人/户和2.69人/户，以及2030年的2.59人/户和2.56人/户；起始平均家庭户规模水平中等的黑龙江省和重庆市则将经历了相对缓慢的下降过程，于2020年接近2.5人/户，随后向2.5人/户收敛；北京、上海的起始平均家庭户规模水平已经低于2.5人/户，随后的预测结果基本在一条水平线上。

本文的平均家庭户规模模拟方程是基于家庭转变第2阶段的数据进行拟合，不适用于已经进入或即将进入家庭转变第3阶段的地区。家庭转变第3阶段地区的模拟和预测应该采用另外的模型，但中国处于家庭转变第3阶段的地区没有足够的数据点进行模型拟合。

五、总结与讨论

基于常规人口数量和家庭数量指标的平均家庭户规模模拟方程，能够在简单数据要求的基础上模拟和预测平均家庭户规模变化过程，对于缺乏动态家庭数据的发展中国家和小区域的家庭动态变化研究有积极意义。

1.模型整体检验显示，平均家庭户规模模拟方程的解释力在78%～98%之间。事后检验显示，利用人口普查时点的家庭规模数据进行校正，中短期模拟的误差可以控制在5%以内，中长期模拟的误差在10%以内。总之，本文的平均家庭户规模模拟方程是一种稳健、简约的模拟或预测方法。

2.从分析结果看，各省的模型拟合参数存在明显的差异，说明中国不同省份的家庭规模结构存在一定的异质性。平均家庭户规模是用于描述家庭规模结构的抽象指标，不同省份的平均家庭户规模模型参数的差异反映的是不同省份的家庭规模结构存在差异，除非不同省份的家庭规模结构趋向同质化，否则模型参数就必然存在差异。因此，本文的结果间接说明中国家庭规模结构存在地区差异。

3.采用省级研究尺度的数据进行方法验证，所得到的结果是“省级”平均水平的模拟或预测结果，如果输入更大(全国)或更小(市级)尺度的数据，则相应得到不同尺度的平均家庭户规模模拟或预测结果。同样，如果输入分城乡的数据，则得到的是分城乡的平均家庭户规模模拟或预测结果。

4.本文的模型能够体现典型的人口学事件，比如，中国20世纪90年代逐步兴起的人口流动，在平均家庭户规模模拟方程中表现为分段Bi-logistic方程的形式。至于诸如生育政策改变等其它人口事件，如果历史数据没有包含这些人口事件的信息，则需假设原有平均家庭户规模变化趋势还会受到人口事件的“干扰”，需要引用其它相关研究结果，修正平均家庭户规模的预测结果。比如：全面两孩政策是中国近年来生育政策的重大调整，它对家庭规模结构或多或少会产生影响，从而使得平均家庭户规模的变化偏离预测轨迹。如果将全面两孩政策的影响纳入本文的模型，应该考虑政策新增出生人口数量[19]对平均家庭户规模的影响[注]在预测期内，新增出生人口不太可能离家立户，考虑全面两孩政策的平均家庭规模为：政策不变的平均家庭规模(2.59)+新增出生人口数量/家庭数量(0.07)。新增出生人口数量引自王广州(2016)的预测结果。。当然，不同人口事件对平均家庭户规模产生不同的影响，不在本文的研究范围，需要基于人口事件对家庭规模结构影响的理论分析，提出人口事件的“干扰”假设，比如全面两孩政策的实施、新型城镇化导致的人口回流等。

5.鉴于家庭结构变化过程和影响因素的复杂性[1]，本文的模拟方程只是对家庭转变第2阶段的平均家庭户规模进行模拟和预测，且使用了较长的时间序列数据，但都是公开途径可以获取的常规数据。如果时间序列不够长，本方法的适用性会受到较大影响，这也是没有对家庭转变第3阶段进行模拟的原因所在。但至少对中国而言，绝大多数地区已经经历了长时间的家庭转变过程并接近家庭转变第2阶段的尾声，本文的方法还是有一定适用性的。