求解分数阶延迟微分方程的卷积Runge-Kutta方法
朱瑞,张根根,肖飞雁,兰海峰
(广西师范大学数学与统计学院,广西 桂林541004)
1.引言
分数阶延迟微分方程(FDDEs)在计算机神经网络[19],流体力学[18],电磁学[11],工程学[20−21]等应用科学领域得到广泛应用.关于分数阶延迟微分方程定性理论,Benchohra等[1]首先讨论了一类带无穷时滞的Riemann-Liouville分数阶微分方程初值问题解的存在性.DENG[2]研究了一类分数阶延迟微分方程解的存在唯一性并得到两个新的存在性和唯一性结果.在分数阶延迟微分方程数值求解方面,Moghaddam[3]提出了利用分数阶有限差分方法求解分数阶延迟微分方程.Mogrado等[4]利用自适应的分数阶向后差分方法求解了一类常延迟线性分数阶微分方程初值问题.Bhalekar等[5]将Adams-Bashforth-Moulton算法扩展到求解分数阶延迟微分方程.WANG[6]又将Adams-Bashforth-Moulton方法与线性插值方法结合来近似分数阶延迟微分方程.Daftardargejji[7]提出了一种新的用于分数阶延迟微分方程的预估校正方法.
另一方面,关于卷积Runge-Kutta方法,Lubich[8−9,13−14]将卷积核进行Lapace变换,利用Runge-Kutta 方法构造了求解分数阶微分方程的数值算法,并给出相应的理论分析结果.接着,在文[10]中给出了基于A-稳定Runge-Kutta方法的卷积积分的误差分析,并证明该方法近似的阶数取决于Runge-Kutta方法的经典阶数和Lapace变换的增长指数.曹学年等[12]构造了求解非线性分数阶微分方程的Radau IIA方法,并证明该方法的相容性,收敛性和稳定性.徐大[22]利用Runge-Kutta方法研究Volterra型积分方程初边值问题,并证明了数值方法的收敛性.
本文基于强A-稳定Runge-Kutta方法,构造了求解非线性分数阶延迟微分方程的离散格式.第三节和第四节分别对数值方法进行了误差分析和稳定性分析.最后给出两个数值算例,以验证提出方法的有效性.
2.数值格式
考虑如下分数阶延迟微分方程初值问题

其中常延迟τ ≥0,φ(k)∈C[−τ,0]为初值函数,f:[0,T]×Rd×Rd→Rd是一个连续映射且满足经典Lipschiz条件

这里L1,L2为常数,符号∥·∥表示空间Rd中的范数.
定义2.1[15]表示Caputo分数阶导数,其定义形式为:

其中l −1<α ≤l,l ∈N,t>0.
定义2.2[15]表示Riemann-Liouville分数阶导数,其定义形式为:
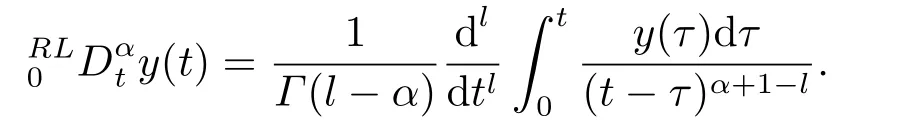
根据Riemann-Liouville分数阶导数与Caputo分数阶导数的关系,微分方程(2.1)等价于以下方程

并且记问题(2.3)的真解为y(t).

应用基于Riemann-Liouville分数阶导数的强A-稳定Runge-Kutta方法[9]

求解(2.3)式,得到在点tn+1=(n+1)h处的离散格式

即

其中


3.误差分析
在给出主要结果之前,我们首先介绍几个有用的引理.
引理3.1[9]假设K(s)在扇形区域|arg(s −c)| <π−ϕ,其中ϕ <π2,c ∈R,存在实数µ,M,使得|K(s)|≤M ·|s|−µ,考虑一个强A稳定的m级p阶Runge-Kutta方法,此时存在一个h0>0,当0 其中,q为级阶,特别地,对于Radau IIA方法有p=2m −1,q=m. 引理3.2[9]在引理3.1的假设条件下,存在h0>0,使得当h 其中n=0与n=1有相同的界限,c,γ,h0仅依赖于方法和引理(3.1)中假设条件中的常数,可以独立于µ. 引理3.3(Gronwall不等式) 令a,b ≥0,h>0,ηi满足 则必有 其中M0=max(|η0|,|η1|,··· ,|ηk−1|). 接下来,我们将给出Runge-Kutta方法的局部截断误差和收敛性分析.记Un为mN维向量,U(1)n=O(hm+1)为Un前(m −1)N个分量,U(2)n=O(hp)+O(hm+1+µ|logh|)为后N个分量. 定理3.1对于分数阶延迟微分方程(2.3),基于m级Runge-Kutta方法的局部截断误差为O(hp)+O(hm+1+µ|logh|)). 证假设Yvj=y(tv+cjh)(v ≤n).由(2.3),(2.6) 及引理3.1 可得 这里ω0,m是矩阵W0=h−α−1(A−1)α的第m行的第m个元素,令hω0,m=h−α,其中为依赖于方法的非零常数.将hα/乘以上式,两边取范数可推出 存在最大步长h0>0,使得则当0 证毕. 定理3.2对于分数阶延迟微分方程(2.3),基于强A-稳定的m级Runge-Kutta方法满足 证记evj=y(tv+cjh)−Yvj,j=1,··· ,m,Ev=(ev1,ev2,··· ,evm)T,由(2.3),(2.6)及引理3.1可得 即 其中,W0=h−α−1(A−1)α为非奇异矩阵.将上式左右两端同时左乘hαAα有 注意到 对于∥En−u∥进行如下讨论. 情况I当n−u ≤0时,y(t−τ)=φ(t−τ)根据(2.4)式可知0.对(3.2)式两边取范数,有 存在h1>0使得(hα1∥Aα∥)−1>L1,则当0 这里C1=max(∥Wv∥,v=0,··· ,n −1), 由引理3.3有 当m ≥2时,∥Un∥=O(hm+1);当m=1时,∥Un∥=O(hp),所以 情况II当n −u ≥0时, 证毕. 定理4.1卷积Runge-Kutta方法求解分数阶延迟微分方程(2.3)是稳定的. 证设{yn+1},{xn+1}分别是由分数阶延迟微分方程(2.3)及其扰动问题 的解,令 其中xn+1=Xnm,yn+1=Ynm. 记σij=Xij−Yij,j=1,··· ,m,ςv=(σv1,···,σvm)T,v=−u,−u+1,··· ,n,ςk(0)=xk(0)−yk(0),k=0,1,··· ,l −1,则 即 注意到 且 对(4.1)式两边同乘hαAα,并两边取范数得 即 取h2为最大步长,且使(hα2∥Aα∥)−1>L1,则当0 即 这里C3,C4为常数,根据引理3.3有 从而 所以数值方法稳定.证毕. 例5.1考虑如下分数阶延迟微分方程问题 其精确解为y=t3. 利用三阶Radau IIA方法,分别取不同步时刻t和不同α在t ∈[0,2]进行数值试验,其绝对误差e如表5.1所示.取h=1/20,α=0.1,0.3,0.5,0.7,0.9时的误差分布图见图5.1. 表5.1 在t=2.0时刻,不同步长h和α下数值解的绝对误差 图5.1 h=1/20时取不同α值的误差分布 图5.2 h=1/40时取不同α值的误差分布 例5.2考虑如下分数阶延迟微分方程问题 其真解为y=t2. 利用三阶Radau IIA方法,分别取不同步长h和不同α在t ∈[0,2]进行数值试验,其绝对误差如表5.2所示.取h=1/40,α=0.1,0.3,0.5,0.7,0.9时的误差分布图见图5.2. 表5.2 在t=2.0时刻,不同步长h和α下数值解的绝对误差










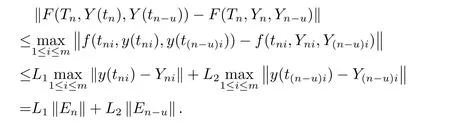

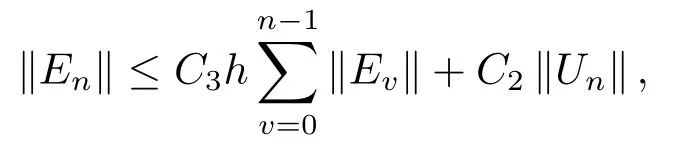





4.稳定性分析








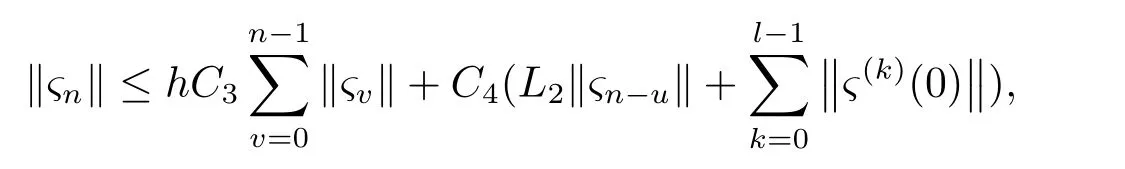


5.数值试验







