蓝牙测距与PDR测角融合的室内定位方法
王晓甜, 毛永毅
(西安邮电大学 电子工程学院, 西安 710121)
室内定位系统在日常生活、工业生产、科学研究、医疗保障等领域应用十分广泛[1-3]。由于在室内环境下蓝牙信号存在着多径效应、信号易衰减、穿透能力弱等问题会造成定位精度大大下降。
目前蓝牙测距、行人航位推算(pedestrian dead reckoning, PDR)等方法是常用的室内定位方法。
目前围绕蓝牙测距方法有很多研究成果。如基于卡尔曼滤波器的室内定位算法[4-6],但是该类算法更适用于线性模型,在噪声较低的情况下定位效果较好,而在非视距(non-line of sight, NLOS)情况下,定位精度和稳定性均受到一定的影响。基于蓝牙网关的接收信号强度指示(received signal strength indication,RSSI)实时校正方法[7],利用定位终端收集蓝牙节点的RSSI,通过存储在服务器上的RSSI波动信息实时调整RSSI;文献[8-10]分析了路径衰减指数对定位精度的影响,在一定程度上实现了对环境噪声和的NLOS误差的补偿,但是定位精度和稳定性仍需进一步提高。
经典行人航位推算(pedestrian dead reckoning, PDR)定位方法利用惯性传感器获取的信息来推算行人的位置和运动轨迹,但是在推算过程中,由于存在着步长和航向角估计误差,会导致误差累积现象[11]。对PDR定位方法改进的研究中,文献[12]通过对矢量域划分校正手机航向角,削弱线性矢量域的累积误差,在保证了PDR的实时性、短时定位高精度性的同时,大幅度削弱了PDR的累计误差从而提高了系统整体的精度、可靠性。文献[13]通过群搜索优化算法(group search optimizer, GSO)算法自动调整正则化权重,以获得更准确的定位结果,并对环境的变化具有一定的适应性。但是,上述定位算法未能完全解决PDR累计误差的问题。
本文拟提出一种融合蓝牙测距与PDR测角的室内定位系统。采用极值-留数消噪算法消除RSSI中的噪声以提高测距精度,利用三次最小二乘算法对蓝牙测距数据和PDR测角数据进行融合确定行人位置。
1 基于极值-留数的RSSI信号降噪
针对RSSI信号提出了一种基于极值-留数的信号分解降噪方法,提取RSSI信号中固有信息的极值和留数,根据这些信息进行重构,以期达到降噪目的。
1.1 极值和留数的求解
首先对信号进行Prony分解得到一系列极值和留数,每个极值和对应的留数代表RSSI信号中的1个成分。设t时刻接收到的RSSI信号为y(t),将其分解成n阶复指数形式[14],其表达式为
(1)
λn=-αn+jωn,γn=Anejθn。
式中:n=1,2,…,p为分解阶次;λn为第n阶极值;系数γn为第n阶留数,它与λn成对出现,为实数或共轭复数;αn为第n阶阻尼系数;ωn为第n阶角频率;An为第n阶各个成分的幅值;θn为第n阶对应相位。
与y(t)对应的等间隔Δt采样的第k=0,1,…,N-1个离散信号为yk,其复指数分解形式[14]的表达式为
(2)
zn=eλnΔt。
为了求解式(1)中的极值和留数,引入高阶微分方程
(3)
(4)
式(1)为式(3)的通解,其中λn为式(3)对应的特征方程式(4)的根。
对于等间隔采样的离散数据yk,式(3)高阶微分方程可变为差分方程
(5)
式中bn为常系数。令bn=1,对应的特征方程为
(6)
求解极值和留数步骤如下:
步骤1将式 (5) 写成矩阵形式
Yb=-y′,
(7)

由于Y和y′已知, 可求出向量b。
步骤2将向量b中的元素bk代入式(6)中,求得特征值zk(k=1,2,…,p)
步骤3将特征值zk代入式(2)中,即可求得对应的留数γk。
1.2 噪声信号分离与剔除
RSSI实测信号y(t)可以看作由2部分组成
y(t)==ys(t)+yn(t)。
(8)
式中:ys(t)为RSSI中不含噪的信号;yn(t)为RSSI中的噪声信号。
对y(t)进行极值-留数分解,得到极值和留数向量,分别表示为
λ=[λs1,λs2,…,λsm,λn1,λn2,…,λnl],
(9)
γ=[γs1,γs2,…,γsm,γn1,γn2,…,γnl]。
(10)
去除噪声对应的极值和留数后,得到不含噪信号的极值和留数向量分别为
λ=[λs1,λs2,…,λsm]
(11)
γ=[γs1,γs2,…,γsm]。
(12)
利用式(2)重构响应信号,得到消除噪声后信号可以表示为
(13)
极值-留数分解降噪算法步骤如下。
步骤1对RSSI信号y(t)进行傅里叶变换,得到信号的对应频谱。
步骤2根据频谱找到峰值对应的频率,以此频率作为中心频率设置频率窗口。
步骤3对RSSI信号y(t)进行极值-留数分解,对极值取绝对值,将复频率转化为实频率,选出频率窗口中的实频率对应的极值和留数,这部分极值和留数可认为是不含噪声的信号对应的极值和留数,通过式(1)将这部分极值和留数重构成时域信号,完成降噪过程。
2 PDR定位
基于PDR定位方法通过加速度计、陀螺仪和磁力计等传感器采集行人运动数据。利用测得的加速度数据推算出行人的步频、步长信息,利用测得的磁力计和陀螺仪数据推算出运动的方位角信息,然后根据前一时刻行人的位置推算出当前时刻行人的位置,PDR定位原理可以表示为
(14)
其中:行人t时刻的位置坐标为(xt,yt),t+1时刻的位置坐标为(xt+1,yt+1);t至t+1时刻行人行走距离为rt+1,行走方向与x坐标轴的夹角为方位角φt+1。
利用有限冲击响应滤波器(finite impulse respond filter, FIR)对测量得到的加速度数据进行滤波以消除噪声。令行人在单步之内的航向角不变,行人在行走时加速度会呈现周期性变化,可以利用峰值检测法测量行人的步频[15]。不同行人的步长存在着一定的差异,利用步长与加速度之间的非线性关系,建立非线性步长估计模型计算步长。令t时刻行人一步内的最大加速度为a1,最小加速度为a2,则步长可以表示为
(15)
其中k1、k2分别为可实时调整的参数,可根据定位的结果自动调整,以适应不同的行人个体。
k1、k2调整方法为:设定k1、k2的初始值并代入到步长公式中,进行定位;经4次定位计算后采用最小二乘法对k1、k2拟合。若拟合后k1、k2的变化值σ≥0.01,则重复上述过程;若k1、k2的变化值σ<0.01,则调整完毕。
方位角可通过计算磁力计参数和陀螺仪参数获得。利用手机内置数字磁罗盘测量磁场信息(Mx,My,Mz),可计算出磁场的水平分量Xh与Yh。则磁航向角可以表示为
(16)
测量φM0后,查表可得其对应的磁偏角,修正后可得行人的航向角φ。
3 蓝牙测距和PDR测角融合定位
3.1 蓝牙测距方程和PDR测角方程
设参与定位的蓝牙基站Bi(i=1,2,…,M)的位置坐标为(xi,yi),其中,B1为主基站。首先采用极值-留数对RSSI信号进行降噪,设RSSI信号服从对数衰减模型,行人与第i个基站之间的信号强度值为pi,行人与第i个基站之间距离为di,pi与di的关系[16]可以表示为
pi=p0-10βlogdi+εi。
(17)
式中:εi为行人与基站Bi间的噪声信号强度值;p0为发射信号功率;β为路径衰减指数。
蓝牙测距和PDR测角示意,如图1所示。
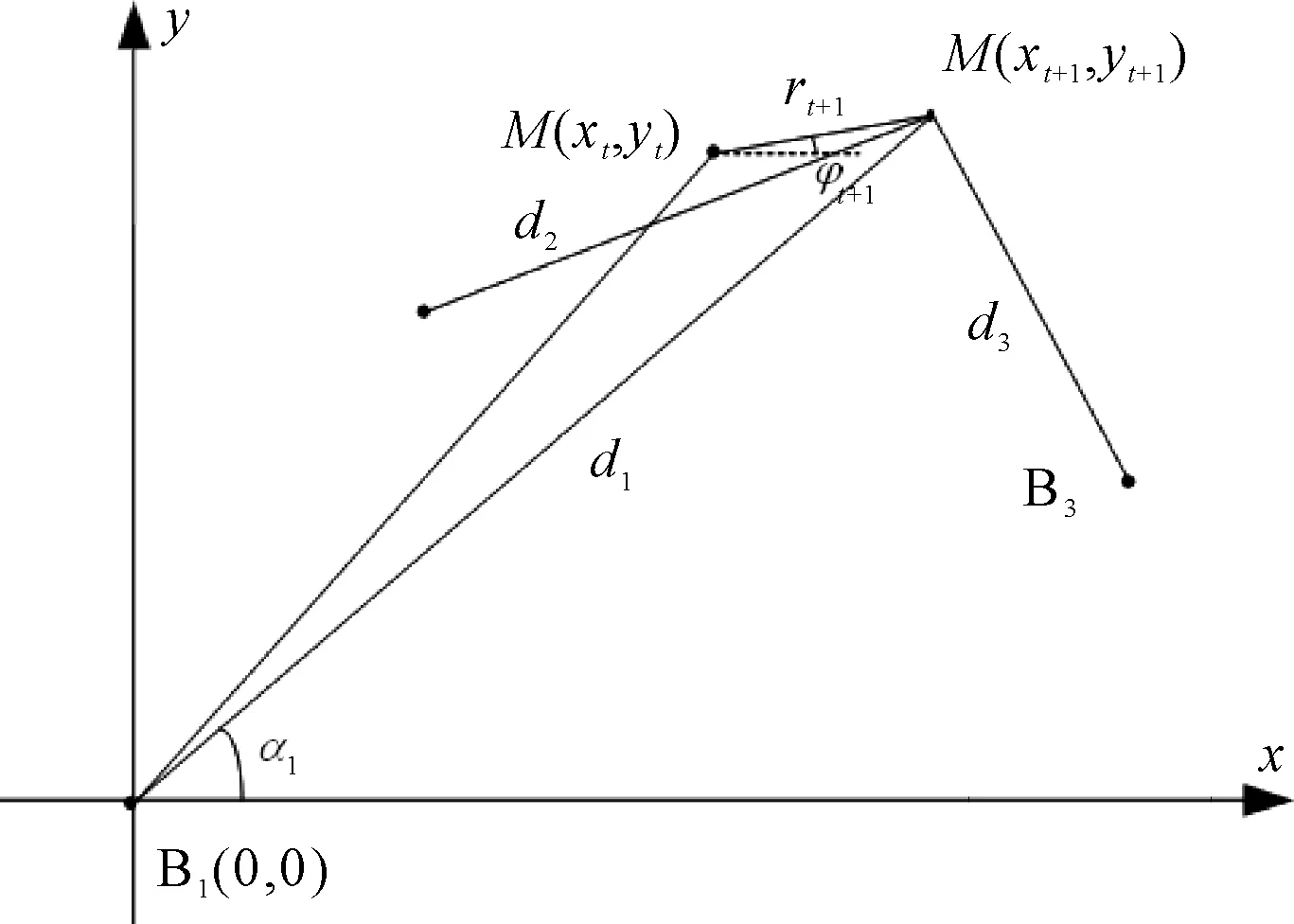
图1 蓝牙测距和PDR测角示意
这里M(xt,yt))为行人t时刻的坐标,M(xt+1,yt+1)为行人t+1时刻的坐标。B1、B2、B3为基站。d1、2、d3分别为行人到基站B1、B2、B3的距离。φt+1为航向角。rt+1为t时刻到t+1时刻的行走距离。
为了推导方便,设主基站B1位于坐标原点。根据di可建立距离方程

(18)
令xi,1=xi-x1,yi,1=yi-y1,di,1=di-d1,则式(18)可改写为
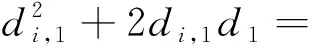
(19)
如此得到行人t+1时刻的位置坐标(xt+1,yt+1)为需要测定的行人位置坐标(x,y),行人与坐标轴横轴的夹角为α1,α2满足
(20)
3.2 融合定位算法
令za=[x,y,d1]T为未知量,建立方程
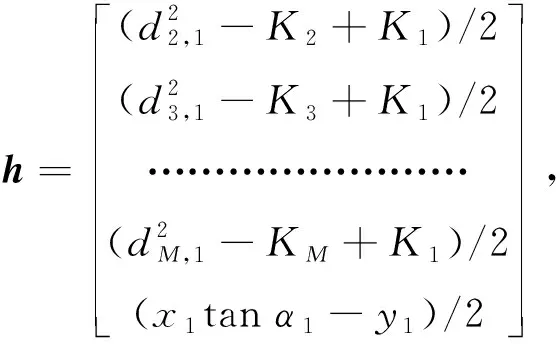
(21)
可将存在的测距误差和角度测量误差表示为误差矢量
(22)

噪声的协方差矩阵可以表示为
当测距误差和测角误差较小时,误差矢量
ψ=BQB,
其中
使用加权最小二乘法(weighted least squares estimation, WLS)进行第一次求解得
(23)
如此,利用za的值可得到新的矩阵B,再进行一次WLS计算可得到改进的行人估计位置。
由于d1与行人位置坐标(x,y)相关,利用这一关系可以进行更为准确的行人位置估计,其步骤如下。
分别计算Δza及za的协方差矩阵
(24)


(25)
ψ′的协方差矩阵为

(26)

依次类推,用第二次WLS计算结果近似代替,则可以得到za′的第三次WLS估计结果
za′=(Ga′TΨ′-1Ga′)-1Ga′TΨ′-1h′。
(27)
最终确定行人的定位结果为

(28)
利用基站的先验信息可以消除式(28)中存在二值解,得到当前的行人位置坐标。
4 实验结果及分析
实验在长12.2 m,宽8.6 m的实验室内进行。融合蓝牙测距与PDR测角的室内定位系统由系统主控制器、蓝牙定位基站和定位目标构成,如图2所示。

图2 融合蓝牙测距与PDR测角的室内定位系统构成
基站个数对基于本文极值-留数降噪定位算法、经典测距定位算法[17]、高斯降噪[18]的定位算法、小波降噪[19]的定位算法的定位误差的影响情况如图3所示。

图3 基站个数对平均误差的影响
可以看出,由于多个基站参与定位,定位信息的冗余有效减小了定位误差,随着定位基站数量的增加,四种算法定位的均方根误差(root mean square error, RMSE)随之减小。本文算法的定位精度明显优于其它定位算法,这是由于采用基于极值-留数的消噪比较有效的消除了室内复杂环境造成的测距误差的影响,因而提高了定位精度。本文算法的RMSE最低可达到0.45 m。
为了验证不同强度噪声对定位算法的影响,在实验室内放置白噪声信号发生器用做干扰源,对不同信噪比情况下的定位精度进行研究。不同信噪比情况下不同算法的平均误差仿真结果如图4所示。
可以看出,随着信噪比的提高,各种定位方法的均方根误差随之减小,其原因是噪声的减小有效的降低了定位误差。信噪比变化对本文算法的定位精度影响较小,表明了经过极值-留数降噪可有效适应环境噪声的变化。

图4 信噪比对平均误差的影响
4种定位方法的定位误差累计分布函数(cumulative distribution function, CDF)如图5所示。

图5 4种定位方法的定位误差累计分布函数
可以看出,文献[17]定位算法只有25%的定位误差达到1 m以内,文献[18]定位算法有28%的定位误差达到1 m以内,文献[19]定位算法有55%的定位误差达到1 m以内,本文算法可达到68%。文献[17]定位算法只有56%的定位误差达到2 m以内,文献[18]定位算法有68%的定位误差达到2 m以内,文献[19]定位算法有78%的定位误差达到2 m以内,而本文算法可达到91%。说明本文算法比其他3种算法有更高可靠性。
为验证融合算法的性能,令行人初始位置位于实验室左上角,行人在实验室内逆时针行走一圈,利用手机以30 Hz的频率采集并保存加速度计、陀螺仪及磁力计的原始数据并上传给上位机。此外,令蓝牙基站测得的RSSI数据也同步上传至上位机,由上位机进行处理和计算得出定位结果。
对经典PDR算法[11]、经典测距算法[17]、本文算法3种算法得到的运动轨迹进行了对比。3种算法的轨迹对比如图6所示。

图6 3种算法的轨迹对比
图6中矩形实线表示真实轨迹,左上角为起点,逆时针匀速行走一周。虚线为经典PDR定位方法绘制的轨迹。经典PDR定位算法在短时间内定位精度比较高,但随着时间的增加误差不断积累导致后面的定位结果远远偏离真实轨迹。点划线为经典测距算法绘制的轨迹,由于没有充分利用历史信息,定位结果会出现定位结果围绕真实轨迹随机跳变的现象。实线是本文算法绘制出的轨迹,比较接近真实轨迹,说明了本文算法有效的减小PDR定位方法存在的误差累积现象和经典测距算法的位置跳变现象,获得了较好的定位与跟踪效果。本文算法在获得测距信息的同时获得了测角信息,最少利用两个基站即可获得行人的位置,这样就可以减少所需定位基站的数量,从而可以有效降低硬件系统成本。
5 结语
由于室内信道环境复杂,非视距传播等因素对定位精度影响较大,单独的定位算法的精度受到很大的影响。本文首先利用极值-留数方法对蓝牙信号进行降噪,然后采用三次最小二乘算法融合降噪后的RSSI数据和PDR数据进行定位计算。实验结果表明,基于极值-留数降噪的蓝牙定位算法的定位精度、可靠性和抗噪性能明显优于文献[17]、文献[18]和文献[19]定位算法,本文算法的RSME最低可达到0.45 m;本文算法最少可以利用两个基站即可完成位置的确定,可以有效的降低系统成本,并且克服了单独采用蓝牙定位出现的定位结果围绕真实轨迹随机跳变的现象和单独采用PDR定位出现的误差积累现象,从而获得较好的定位跟踪效果。

