基于最小平方QR分解的改进鲁棒特征选择
支晓斌, 武少茹
(1.西安邮电大学 理学院, 陕西 西安 710121; 2.西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
特征选择在模式识别领域中,依据特定的准则从原始特征空间中选择一个特征子集,以实现低维度和准确的数据表示[1]。在实际应用过程中,通常会遇到高维数据集。数据的高维度性不仅增加了算法的计算时间,而且会对算法性能产生不利影响[2-3]。因此,高维数据的特征选择方法已成为重点研究问题[4-5]。目前,基于结构化稀疏诱导技术的特征选择方法[6]将稀疏诱导正则化技术与回归或判别分析等机器学习算法相结合,不仅可以准确地选择出与类标签强相关的特征,同时还具有特征选择的稳定性,应用较为广泛。但是,其在对高维数据进行特征选择时,仍容易出现计算开销过大的问题[7-9]。
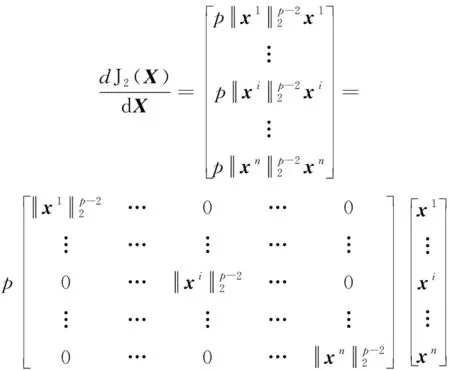
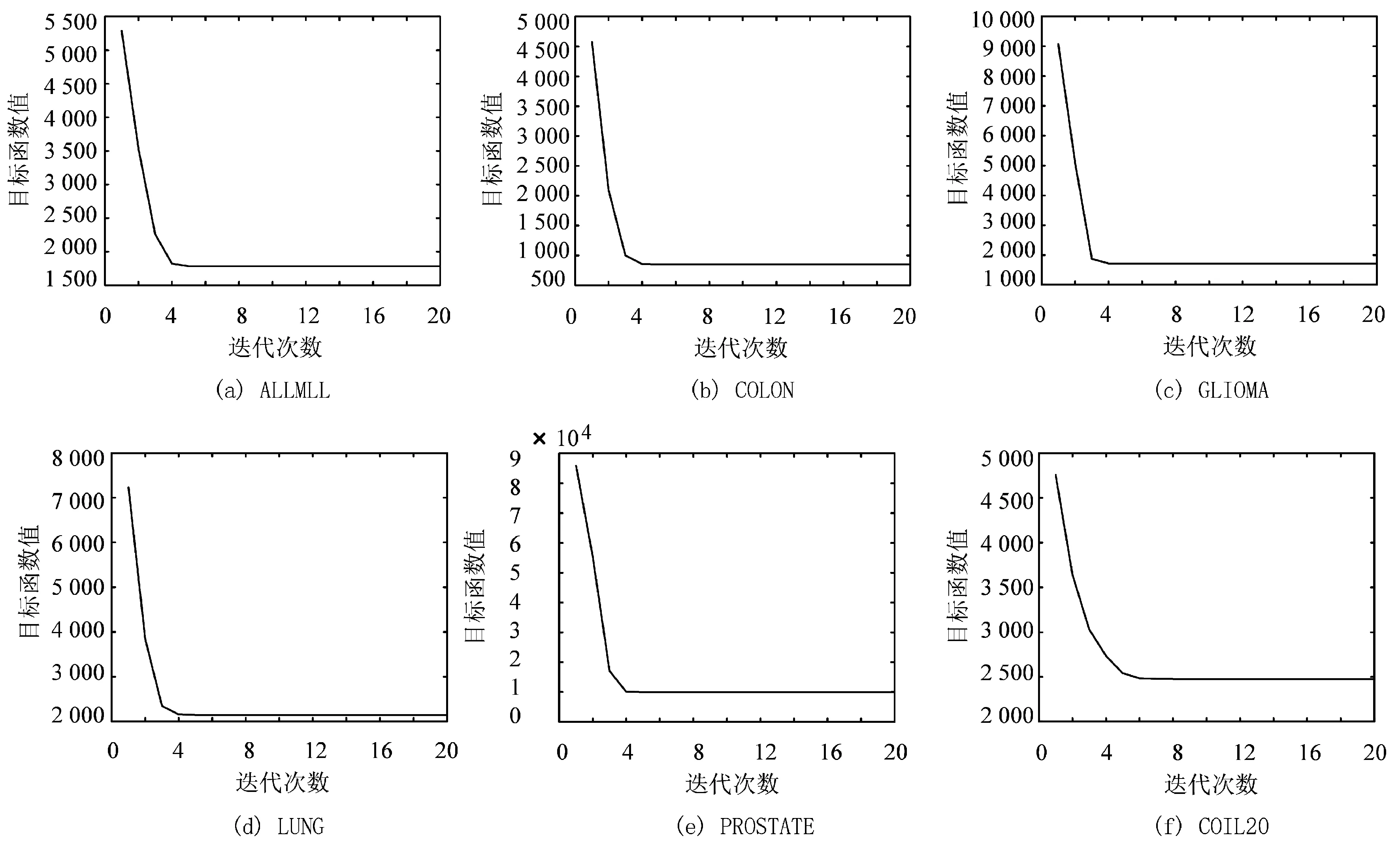
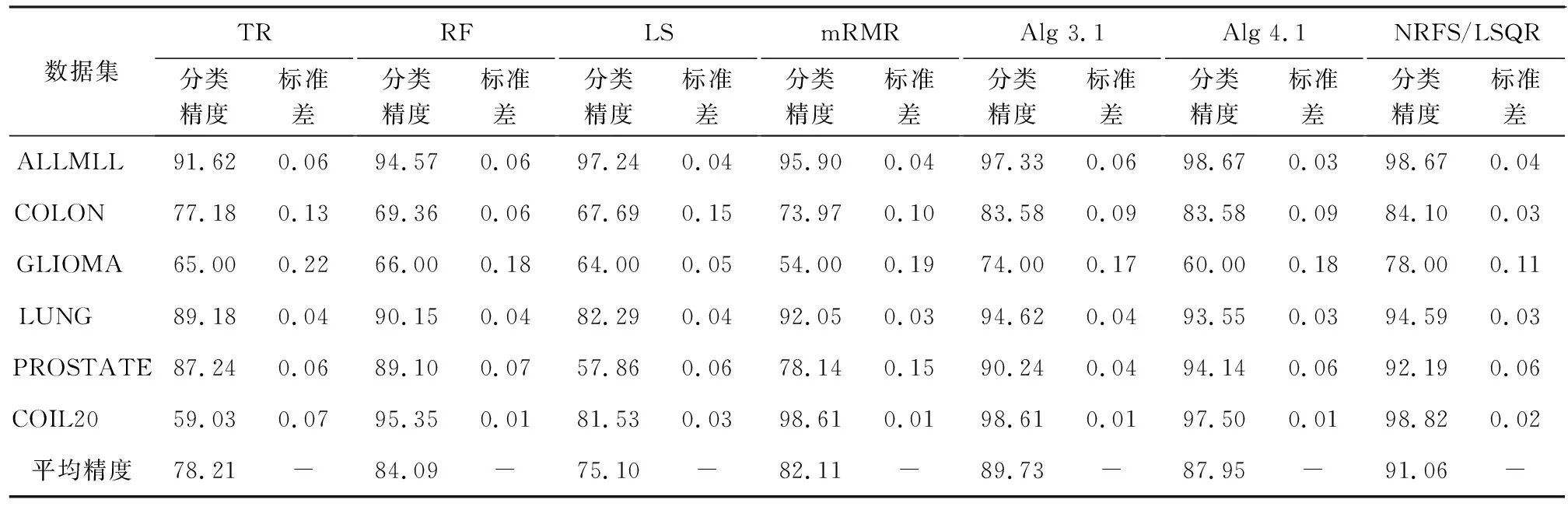
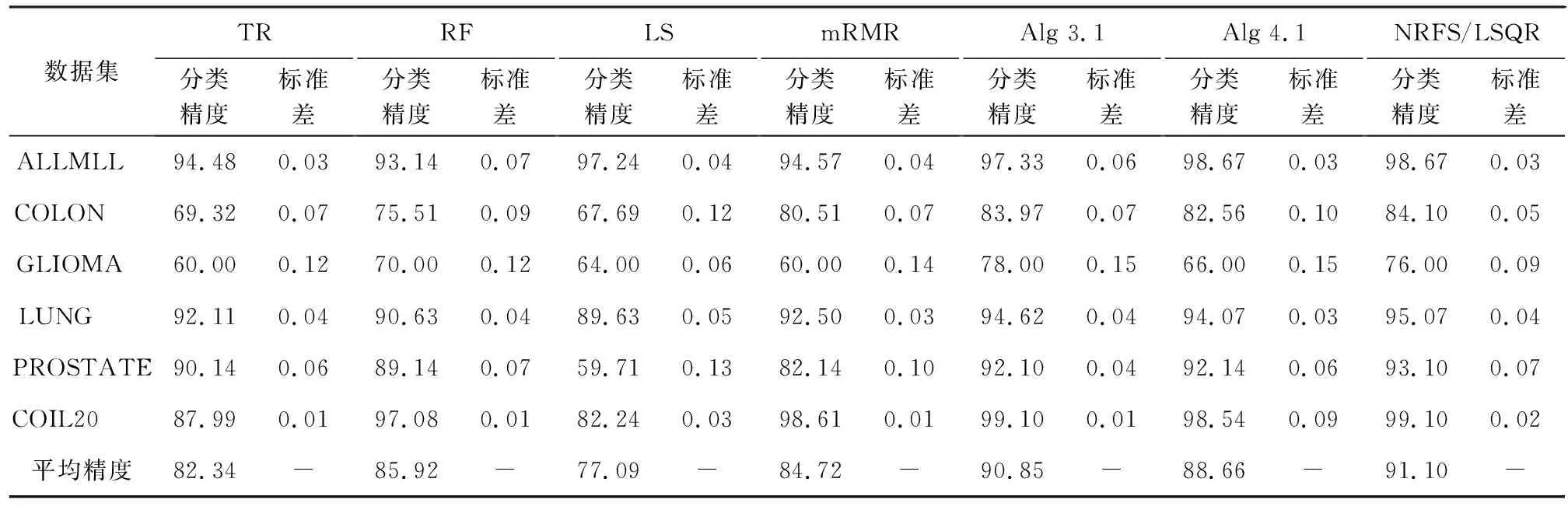
基于结构化稀疏诱导技术的特征选择方法可分为基于向量范数和基于矩阵范数两类特征选择。相比于基于向量范数的特征选择只能解决二分类问题,基于矩阵范数的特征选择可解决多分类问题[6]。为了解决多分类问题,鲁棒特征选择算法(robust feature selection,RFS)[8]使用l2,1-范数代替l1-范数作为正则化项,将鲁棒最小二乘回归(robust least squares regression, RLSR)和l2,1-范数正则化结合,实现了鲁棒的特征选择。但在其每次迭代过程中都包含矩阵求逆运算,使得对高维数据具有较高的时间复杂度,并且RFS对数据的适应性较差。为避免RFS存在的问题,广义的鲁棒特征选择算法(general robust feature selection,GRFS)[9]将RFS中回归问题的损失函数和正则化项均推广为l2,p-范数(0 鉴于GRFS中存在分类精度差的问题,本文提出一种基于最小平方QR分解(least square QR-factorization, LSQR)算法[10]的鲁棒特征选择算法(LSQR based new robust feature selection,NRFS/LSQR)。该算法将GRFS问题转化为迭代重加权最小二乘(iterative re-weighted least squares, IRLS)问题[11],在迭代过程中构造加权数据矩阵和加权类标签矩阵,并利用LSQR求解由二者构成的线性方程组问题,以期保证算法计算效率的同时提高算法精度。 矩阵范数是基于构化稀疏诱导技术的特征选择方法实现特征选择的重要工具之一。矩阵的lr,p-范数被定义为矩阵所有行的lr-范数构成的向量的lp-范数[6]。当r=2,p=1时,矩阵M∈n×d的l2,1-范数[1]定义为 当r=2,p>0时,矩阵M∈n×d的l2, p-范数[9]定义为 其中mi表示矩阵M的第i行,mj表示矩阵M的第j列。 RFS算法通过对鲁棒最小二乘回归的损失函数添加l2,1-范数正则化项约束,使得每个特征对所有的数据点具有一致的重要性,从而实现鲁棒特征选择[8]。 假设在d维空间中存在n个属于c类的数据样本矩阵A=[a1,a2,…,an]∈d×n,对应的类标签矩阵为n×c,则RFS[8]算法可描述为 (1) 其中,γ为正则化参数,X为回归系数矩阵。 将问题(1)转化为与之等价的有约束极值问题 (2) 利用拉格朗日乘子法求解问题(2),得到 Y=D-1MT(MD-1MT)-1B, GRFS算法[9]是RFS算法的广义形式,即从基于l2,1-范数的形式推广成为基于l2,p-范数(0 (3) 采用与RFS相似的解法,可解此目标函数。但是,这种方法对于样本数较多的数据集具有时间复杂度高的缺点。为避免在每次迭代时都去进行矩阵求逆运算,采用一步梯度投影替代求逆运算,使其时间复杂度达到O(cm2),从而提高算法的运行速度。 基于l2, p-范数的GRFS算法采用一步梯度投影替代了求逆运算,虽然提高了算法的运行效率,但是,运算过程中的数值近似在一定程度上降低了算法的精度。因此,NRFS/LSQR算法先将问题(3)转化为迭代重加权最小二乘问题,在迭代过程中不断更新加权数据矩阵和加权的类标签矩阵,由二者构成线性方程组问题,再利用LSQR算法[10]求解此问题。 令鲁棒最小二乘回归损失函数 正则化项 则问题(3)可表示为 J(X)=J1(X)+γJ2(X)。 (4) 利用式(4)对X进行求导,并令导数为0,得到 (5) 又因 J1(X)对列xj求导,可得 (6) 根据加权数据矩阵 A′=[w1a1,…,wnan], (7) 第j类数据的加权标签 (8) 其中B′为加权的类标签矩阵,即 (9) J2(X)对行xi求导有 则J2(X)对X的导数为 由此可得对角矩阵D的第i个对角元素为 (10) 则J2(X)对X的导数的矩阵形式为 (11) 将式(8)和式(11)带入式(5)得 p[A′A′TX-A′B′]+pγDX=0 整理得到 (A′A′T+γD)X=A′B′。 (12) (A″A″T)X=A″B″。 (13) 式(13)即为问题(3)的转化问题,可利用LSQR算法求解。因X的求解依赖于D,D又需由X计算得到,所以NRFS/LSQR算法是一个迭代的过程。 在NRFS/LSQR算法的具体实现中,把最小二乘问题[10] (14) 利用LSQR算法求解,将得到的解(AAT+γI)†AB作为X的初始值,即 X0=(AAT+γI)†AB。 NRFS/LSQR算法的具体步骤如下。 步骤1对原始数据矩阵A和类标签矩阵B执行规范化和中心化过程。 步骤2以问题(14)的解作为X的初始值,即取X0=(AAT+γI)†AB。 步骤4将X0带入式(6)计算得到权重wi,i=1,2,…,n。 步骤7根据更新后的A″和B″重构问题(13),并利用LSQR算法求解得到X。 为验证NRFS/LSQR算法的有效性,首先对该算法的收敛性进行分析,再将其与救援扩展(relief-f, RF)算法[12]、拉普拉斯分值(laplacian score, LS)算法[13]、迹比(trace ratio, TR)算法[14]、最大相关最小冗余(minimal-Redundancy Maximal-Relevance criterion, mRMR)算法[15]和GRFS算法等5种特征选择算法进行分类精度对比,评估其特征选择能力。 实验环境为Intel Core i5-8500 3.00 GHz CPU、16 GB运行内存、Windows 10操作系统和MATLAB 2016a。 实验选取ALLAML数据集[9]、COLON数据集[1]、GLIOMA数据集[9]、LUNG数据集[9]、PROSTATE数据集[9]和COIL20数据集[1]等6个数据集。其中COLON数据集具有相对较少的样本数以及维数,COIL20数据集具有相对较多的样本数,增加了实验的复杂性,使得实验结果更加可靠。各数据集的相关统计特性如表1所示。 表1 6个数据集的相关特性 当参数p=1,γ=10时,NRFS/LSQR算法的目标函数值在6个数据集上随迭代次数的变化趋势如图1所示。从图1可以看出,NRFS/LSQR算法的目标函数值在迭代过程中呈非增趋势且在第6次迭代之后都收敛于一个固定值。故NRFS/LSQR算法具有较快的收敛速度。 使用最近邻法作为分类器度量各特征选择算法的特征选择能力。GRFS和NRFS/LSQR中的正则化参数γ设置为{10-6, 10-5, 10-4, 10-3, 10-2, 10-1, 100, 101, 102, 103, 104, 105, 106},p设置为{0.25, 0.5, 0.75, 1},选取所有参数组合中最优的结果作为最终结果。在实验过程中随机选取80%的样本作为训练集,剩余的20%样本作为测试集,将这个过程重复5次,取5次结果的平均值作为最终的结果。被选特征数分别为20、 40、60和80时各特征选择算法的分类精度和标准差分别如表2,表3,表4和表5所示。各表中的Alg 3.1和Alg 4.1是GRFS算法在文献[9]中的两个算法。 图1 迭代变化趋势曲线 表2 被选特征数为20时7种特征选择算法在6个数据集上的分类精度及标准差/% 表3 被选特征数为40时7种特征选择算法在6个数据集上的分类精度及标准差/% 表4 被选特征数为60时7种特征选择算法在6个数据集上的分类精度及标准差/% 表5 被选特征数为80时7种特征选择算法在6个数据集上的分类精度及标准差/% 由表2、表3、表4和表5可以看出,NRFS/LSQR算法的平均分类精度均高于其他5种特征选择算法,尤其是在被选特征数为20时,NRFS/LSQR算法的分类精度比其他5种算法中的最高精度还高出2.76%。因此,NRFS/LSQR算法具有较强的特征选择能力。 NRFS/LSQR算法通过构造加权的数据矩阵和类标签矩阵,将基于l2,p-范数的鲁棒特征选择问题转化为迭代重加权最小二乘问题,并利用LSQR求解迭代过程中的最小二乘问题,避免了因数值近似带来的精度损失。实验结果表明,NRFS/LSQR算法的特征选择能力优于其他几种特征选择算法,且收敛速度快。1 鲁棒特征选择算法
1.1 矩阵范数
1.2 基于l2,1-范数的鲁棒特征选择算法
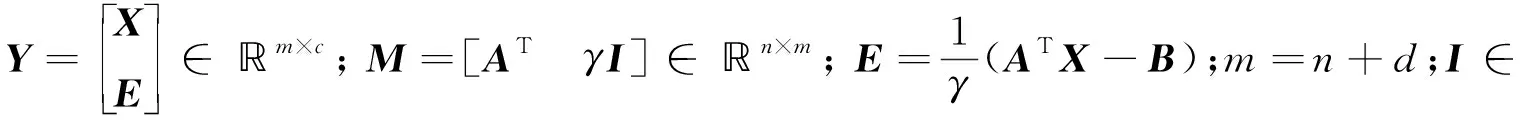

1.3 基于l2,p-范数的鲁棒特征选择算法
2 基于LSQR算法的鲁棒特征选择算法
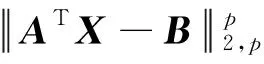
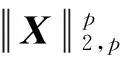
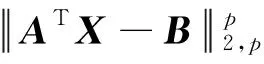


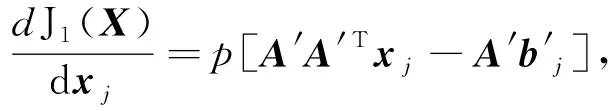


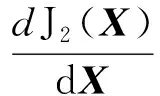
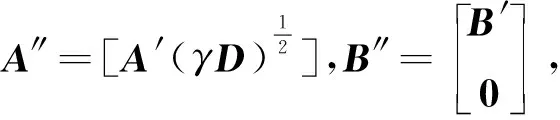
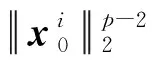
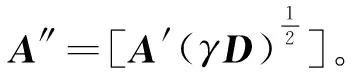
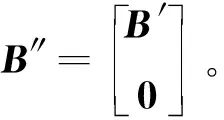

3 实验结果及分析
3.1 实验设置
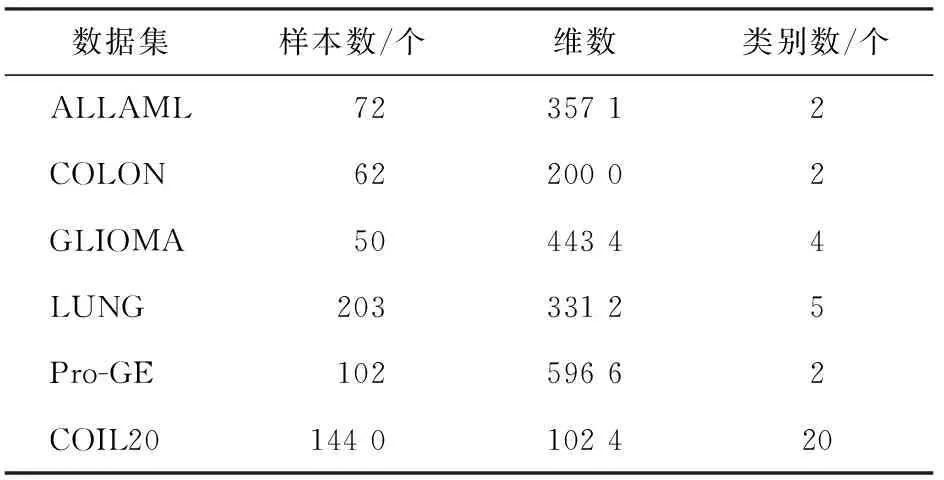
3.2 收敛性分析
3.3 分类精度对比


4 结语

