婴儿培养箱温度场和流场均匀性的分析优化

周峰，唐火红，骆敏舟

1. 合肥工业大学 a. 智能制造技术研究院；b. 机械工程学院，安徽 合肥 230009；2. 江苏集萃智能制造技术研究所有限公司，江苏 南京 211800

引言

婴儿培养箱主要用于早产儿或患病儿的恒温培养，为早产儿或患病儿提供一个恒温恒湿的类似母体的适宜环境，减少外界环境对婴儿的不良影响，保证婴儿的正常生长发育[1-2]。培养箱服务人群的特殊性决定了其良好的温度性能相对重要，所以对培养箱内部温度场均匀性的研究具有重要意义[3-4]。kim等[5]采用数值模拟的方法对婴儿培养箱内的气流运动状态以及婴儿周围的气流状态进行了研究。Ginalsk等[6]通过数值模拟的方法研究了在培养箱内某些部位添加有机玻璃板对内部气流温度的影响。Wongkamhang等[7]建立了双层壁面的培养箱模型，研究了多出口多入口对箱内温度的影响。但以上研究均未对箱内温度场和流场的均匀性做优化。文中通过正交试验与数值分析的方法，研究影响培养箱温度均匀性和气流速度均匀性的因素，优化培养箱温度场和流场的均匀性。文中采用在箱体长度方向的两侧入风，宽度方向的两侧出风的方式，在底面上设置两个入风口和两个出风口。相比于传统的一侧入风一侧出风的培养箱，这种进出风口的设置能缩短箱内气流的流动距离，改善入风口侧温度高，出风口侧温度低的状况，提高培养箱内的温度均匀性，同时也能提高加热速度。

正交试验法是一种研究与处理多因素试验的一种科学方法，利用正交表来安排试验，具有均衡分散、整齐可比的特点，能在考察范围内选出代表性强的少数试验条件做到均衡抽样，能够通过少数的试验次数找到最优的方案[8-9]。传统的正交试验多采用加工样机进行实际试验的方法进行分析，既费时又费力，而计算机数值模拟在流体领域的广泛应用，则可以省去繁琐的实际试验而得到较为准确的结果。文中以培养箱内气流为研究对象，应用计算流体动力学（Computational Fluid Dynamics，CFD）方法和正交试验的方法对婴儿培养箱进行数值仿真和优化设计，找出性能较优的设计方案。

1 正交试验设计

婴儿培养箱利用热对流的方式对箱内空气进行加热[10]，为了研究箱内的温度场和流场的情况，必须对箱内气流流动进行研究。影响箱内气流的因素有很多，文中选取入口大小（A）、出口大小（B）、入口风速（C）、入口角度（D）作为正交试验的四个因素来分析。入口和出口均为条缝式，按照已有的经验确定各因素3个水平。根据表1所示的因素和水平个数选择正交表，设计9组试验并填入正交表，得到试验方案（表2）。

表1 因素-水平表

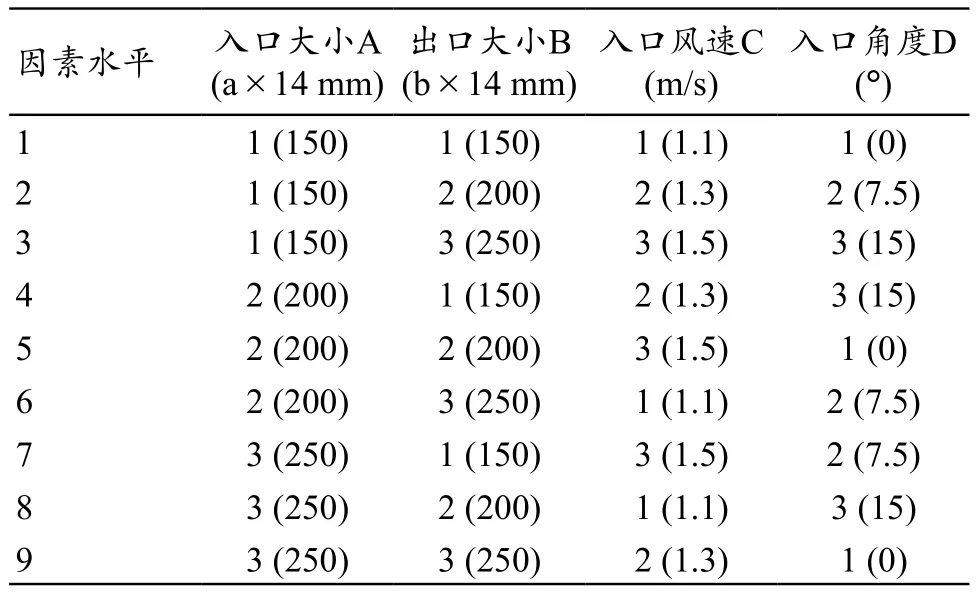
表2 试验方案表

2 数值计算

2.1 计算模型的建立

利用SolidWorks对婴儿培养箱箱内流场区域进行三维建模，简化内部结构，如图1a所示。坐标原点设置在箱体底面的中心处。由于箱体为对称结构，所以取流场区域的四分之一来进行研究，这样可以减少划分网格后的总网格数，提高计算效率，如图1b所示。在ansys workbench中将模型导入DesignModeler，在DesignModeler中建立入口和出口，如图1c所示。然后将DesignModeler数据导入ICEM 进行网格划分。

图1 婴儿培养箱箱内流场区域三维建模简化图

2.2 网格划分

在ICEM中进行网格划分。结构网格的质量较高，网格生成的数据结构简单，计算速度较快，网格容易实现区域边界的拟合，数值模拟时容易收敛[11]。培养箱箱体形状比较规则，采用六面体结构网格，节点数约为345558，单元数约361728，然后将网格数据导入到fluent中。流场的有限元模型及网格如图2所示。

图2 有限元模型及网格

2.3 求解设置

2.3.1 边界条件

在fluent中进行边界条件的设置，入口采用速度边界条件，包括入口气流速度、湍流强度和水利直径等。入口方向通过xyz坐标轴上的速度分量来确定。湍流强度和水力直径的计算如下[12]：

其中，D为水力直径，A为流体流过的截面积，P为湿周。

其中，Re为雷诺数，ρ为流体密度，v为流体速度，d为水力直径，μ为流体的黏性系数。

其中，I为湍流强度，Re为雷诺数。

设定入口温度边界条件为308 K，出口采用出流边界条件，四周和上壁面采用无滑移壁面边界条件。箱体为双层有机玻璃罩，中间为空气，壁面的热边界条件采用第三类边界条件conduction来模拟三层壁面结构，外壁面大气温度设置为常温25℃，即298 K。箱体底面为设备箱，设置下壁面为无滑移边界条件，热边界条件为第三类边界条件，外壁面温度假定比外界高出5℃，即303 K。婴儿床在箱体内，设置为绝热无滑移边界条件。两个对称面设置为对称边界条件。

2.3.2 数学模型

在建立数学模型时做如下假设：① 培养箱内的空气不可压缩并且符合boussinesq假设；② 培养箱内的空气流动为稳态湍流；③ 培养箱放置在室内，不考虑热辐射的影响；④ 不考虑湿度的影响；⑤ 假定箱体为密封，忽略泄露的影响。

标准k-ε模型在科学研究及工程实践中得到了广泛的检验和应用，但其用在强旋流、弯曲壁面流动或弯曲线流动时，会产生一定的失真[13]。培养箱内的气流流动较为复杂，会产生旋流以及流线较大的弯曲，所以采用改进的Realizable k-ε模型；近壁面采用标准壁面函数。

2.3.3 基本控制方程

CFD给出了流体流动的控制方程——质量守恒方程、动量守恒方程和能量守恒方程[13]。（1）质量守恒方程：

式中，ρ为流体的密度，单位kg/m3；t为时间，单位s；为速度矢量，单位m/s。

（2）动量守恒方程：

式中，p为作用在流体微元体上的压力，Su、Sv、Sw为广义源项。

（3）能量守恒方程：

式中，cp为比热容，T为温度，k为流体的传热系数，ST为流体的内热源及由于黏性作用流体机械能转换为热能的部分，黏性耗散项。

3 计算结果及分析

3.1 箱体内流动分析

根据表2的试验方案，分别对9组试验进行计算得到计算结果。图3、图4为各组试验流场区域的流线图和婴儿床上方10 cm即Z=200 mm处的温度云图。

从流线图中可以看，9组试验气流运动情况大体是相同的。两侧入口处的气流进入箱体后向上运动，碰到上壁面后沿上壁面向中间移动，在中间位置两侧气流相遇，然后共同向下运动，遇到婴儿床后散开，一部分到达出口处流出箱体，另一部分向两侧运动，在遇到入口气流后被入口气流裹挟向上运动，形成两个明显的大尺寸的涡流。随着气流的运动，其流线颜色逐渐趋于深蓝色，说明气流速度逐渐减小，到达婴儿床时流线颜色较均匀，速度也均小于0.35 m/s，其速度大小符合婴儿培养箱安全专用要求[14]。

图3 各组试验流线图

图4 Z=200 mm截面温度云图

从温度云图上看，9组试验温度分布的形式是相同的，两侧入口区域和中间气流汇聚区域颜色较深温度较高，距离两侧和中间区域较远的地方，在大约出口区域的两边形成四个明显的颜色较浅的低温区域，同时贴近壁面的区域受外界低温的影响较大颜色较浅温度较低。

试验1/2/3、试验4/5/6、试验7/8/9入口大小逐渐增大，入口的高温气流影响的区域也越大，四个低温区的面积较小；试验1/5/9、试验2/6/7、试验3/4/8入口角度为逐渐增大，在入口角度从0°增大到7.5°时，高温区离壁面距离有所增大但不明显，这是由于入口气流受附壁作用的影响，流线明显被拉近壁面；当入口角度增大到15°时，流线距离壁面足够远，没有受到壁面的影响，高温区域距离壁面最远，所以，在入口角度逐渐增大的过程中，高温区逐渐靠近中心区域，使得低温区域的面积也减小。

3.2 极差分析

通过极差分析法分析各因素对温度场和气流速度场的影响状况，由于婴儿被放置在婴儿床上，培养箱其他地方的温度对婴儿的影响不大，在计算域内婴儿床上方10 cm处和20 cm处的平面上，各选取五个点[15-16]（一个中心点和四个角点），总计10个点，在fluent中输出这10个点的温度和速度值、平均值和标准差，通过计算得到温度不均匀系数和气流的速度不均匀系数，作为评价指标。

通过对称，可以得到婴儿床上方26个点的温度和速度数据，符合婴儿培养箱安全专用要求中的5个点的取点要求。温度和速度不均匀系数定义如下[17]：

由于温度不均匀系数数值较小，将其统一放大1000倍，放大后不影响数据的分析。

计算结果和极差分析如表3、表4所示。其中KT、KV为温度不均匀系数和速度不均匀系数，T1、T2、T3分别为相应水平下的温度指标之和，RT为温度指标极差值，V1、V2、V3分别为相应水平下的速度指标之和，为速度指标极差值。

表3 试验方案及结果计算表

表4 极差分析表

由表4可知，不同试验参数下温度不均匀系数和速度不均匀系数的极差值R是不同的，说明所选取的不同因素对温度均匀性和速度均匀性影响不同。极差值越大，说明该因素的不同水平对应的试验结果的差异越大，影响越也大，为主要因素；相反，极差值越小，说明该因素的不同水平对应的试验结果的差异越小，影响也越小，为次要因素。比较表4中各因素的极差值大小可知，影响温度不均匀系数和速度不均匀系数的主次因素描述如下。

温度均匀性：

入口角度—出口大小—入口大小—入口风速

速度均匀性：

出口大小—入口风速—入口角度—入口大小

为了直观起见，用因素的水平作横坐标，温度不均匀系数和速度不均匀系数为纵坐标，做出指标-因素关系图（图 5）。

图5 指标-因素关系图

温度不均匀系数和速度不均匀系数越小时，温度和速度越均匀，由图5可以看出：① 入口大小在从小到大的变化过程中，温度和速度不均匀系数均为持续减小，取A3时最好；② 出口大小在从小到大的变化过程中，温度和速度不均匀系数均为先下降再上升，取B2最好；③ 入口风速在1.1 m/s到1.5 m/s增大的过程中，温度不均匀系数先降低，后有微幅上升，取C2最好，速度不均匀系数持续增大，取C1最好；④ 入口角度在0°到15°的变化过程中，温度不均匀系数一直下降，取D3最好，速度不均匀系数先下降后升高，取D2最好。

可见，入口大小A和出口大小B对温度不均匀系数和速度不均匀系数的影响趋势是相同的，好坏顺序依次为A3A2A1、B2B1B3，所以入口大小和出口大小取A3B2最好；对于入口风速C来说，C3时温度均匀性最好，C1时速度均匀性最好，在入口风速取C2和C3时温度不均匀系数相差很小，速度不均匀系数相差很大，同时，温度均匀性和速度均匀性的重要程度不同，温度均匀性的重要程度更高，综合来看入口风速取C2最好；对于入口角度来说，D3时温度均匀性最好，D2时速度均匀性最好，入口角度在取D2和D3时温度不均匀系数和速度不均匀系数的差值不大，同时考虑到温度均匀性的重要程度更高，所以取D3最好。由此可以得出培养箱保温性能可能的最佳方案为A3B2C2D3。

由于A3B2C2D3组合未在9组试验中出现，以方案A3B2C2D3做第10组验证试验，经过数值计算结果数据如表5所示。

表5 方案A3B2C2D3结果数据

比较表3和表5的温度不均匀系数和速度不均匀系数，第10组试验的温度不均匀系数为10组试验中最小的，速度不均匀系数仅比第2组和第8组大，比其他组都小。第10组试验中，相对重要的指标温度均匀性达到了最优，相对不重要的指标速度均匀性达到了较好的水平。说明利用正交试验所得的优化组合是有效的。确定最佳方案为A3B2C2D3，即入口大小250×14 mm，出口大小200×14 mm，入口风速1.3 m/s，入口角度 15 °。

4 结论

利用正交试验的设计方法和数值计算的方法对婴儿培养箱的温度场和流场进行优化，通过正交试验的极差分析发现影响培养箱温度场均匀性的主次因素依次为入口角度、出口大小、入口大小、入口风速；影响培养箱速度均匀性的主次因素依次为出口大小、入口风速、入口角度、入口大小，并得到最优的方案为A3B2C2D3。

入口大小和出口大小对温度不均匀系数和速度不均匀系数的影响趋势是相同的，入口越大，温度均匀性和速度均匀性越好，出口在从小到大变化过程中温度和速度均匀性先变好后变坏；入口风速和入口角度对温度不均匀系数和速度不均匀系数的影响趋势是不同的，入口风速从小变大，温度均匀性为变好的趋势，而速度均匀性为变坏的趋势，入口角度从小变大，温度均匀性为变好趋势，速度均匀性为先变好后变坏。

经过验证试验，优化后的培养箱内温度均匀性和气流速度均匀性得到提高，说明正交试验的方法对培养箱的性能优化是可行的，可为后续的设计提供参考。