分流式柔性铰六维力传感器刚度分析与结构优化

王永立 路 懿

(燕山大学机械工程学院， 秦皇岛 066004)

0 引言

六维力/力矩传感器能够测量3个方向的力和3个方向的力矩，具有良好的应用前景。但传感器性能受到设计原理、结构、制造误差等因素的影响，严重制约着传感器的测量精度。如何在稳定可靠且具有良好互换性的前提下提高传感器精度是当前科研工作者面临的难度大且具有挑战性的研究课题。

目前已有的六维力传感器中，KANG[1]研制了一种 Stewart结构六维力传感器，通过力加载实验，找出了影响误差的因素。KIM[2]采用十字梁结构，开发了机器人足部和手爪上的六维力传感器。在国内，高峰等[3]研制了微型六维力传感器，该传感器用于机器人手腕和手指，用弹性铰链代替了传统的球面副结构。JIA等[4]研制了一种轴用六维力传感器，完成了该传感器理论模型，并用有限元方法进行了验证，完成了标定实验研究。ZHAO等[5]提出了一种基于 Stewart结构的预紧式六维力传感器，并针对样机进行了实验研究。LU等[6]提出了一种刚柔混合结构三腿六维力传感器，并建立了传感器静力模型和刚度模型，通过有限元分析验证了理论模型，进行了加载标定实验。文献[7-9]提出了多种超静定结构的六维力传感器，对其超静定结构进行受力分析，得到了外载与传感器各分支受力间的映射关系，并进行了结构参数优化。文献[10-13]研制了多种过约束正交并联六维力传感器，提出了多项适用于该类传感器的性能指标。

已有的六维力传感器均为一体化结构，具有刚度高、结构紧凑等优点，但这些六维力传感器仍存在一些问题：①目前商用六维力传感器多采用贴应变片方式采集信号，其应变片粘贴的位置、应变片空间布置方式、梁的加工精度对传感器性能影响很大，不易保证其高精度和高可靠性。而且长期使用过程中，一旦应变片损坏，只能整体更换，有些工况下在现场需要再次进行标定后才能使用，费时费力。同时一些商用传感器外载和测力单元之间的映射关系缺乏合理的理论依据。②Stewart型六维力传感器需进行整体预紧，预紧力大小难控制，预紧力导致整体量程减小，测量可重复性差。而且这种传感器结构是超静定的，整体标定困难，施加动态载荷时不易保证精度。③力敏元件中采用球铰的六维力传感器由于球铰间隙的存在，对测量精度有一定的影响，而且球铰无法承受重载。

本文以一种等效为3-RPS并联分支的测力支架为基础，基于其静力的理论模型，结合柔性铰链，设计一种柔性铰并联六维力传感器。

1 柔性铰六维力传感器结构

柔性铰链可以消除传统并联机构中刚性铰链的间隙和运动回程差，具有无摩擦、无磨损、无需润滑、一体化加工等优势，可获得很高的运动精度和运动分辨率[14-15]。本文设计的柔性铰六维力传感器结构如图1所示，包括1个基座、3个弹性测力支架、6个标准拉压力传感器即测力单元、1个加载平台和3个螺柱。

图1 柔性铰六维力传感器结构Fig.1 Structure of six-dimensional sensor with flexure hinge1.基座 2.测力单元 3.测力支架 4.加载平台 5.螺柱

装置的3个测力支架结构相同，圆周分布于基座和加载平台之间。弹性测力分支用高强度铝合金线切割加工而成，其结构简图如图2所示。该结构含有4个二元杆和2个三元杆，二元杆所用转动副R的轴线全部平行，其中柔性移动副P由内外刚性柱和上下两个弹性臂构成刚柔一体的平行四边形框架。测力单元量程为50 kg，其上、下端通过螺栓连接在弹性测力支架上。加载平台与测力分支以转动副的形式用螺柱连接。测力支架上下两个转动副共线使测力单元处只受轴向拉压力，保证了测量的准确性。传感器受外载时，6个测力单元产生信号，通过静力模型可以求得所受外载的所有力和力矩分量的大小和方向。

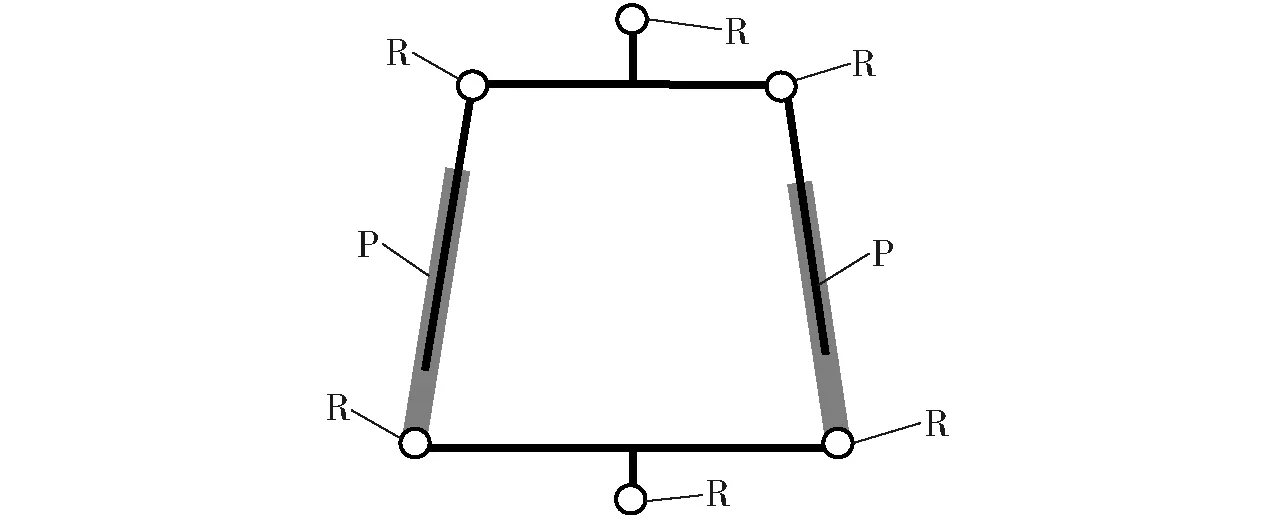
图2 弹性测力分支结构简图Fig.2 Structural diagram of elastic branch

2 柔性铰六维力传感器静力模型

支架与上平台联接处由3个转轴各异的柔性铰链构成，在受力分析时可以等效为球副。平行四边形框架可等效为移动副。故外载荷下该传感器支架的微变形效果可等效为3-RPS构型的变形效果，本文利用3-RPS构型的静力模型寻求传感器与外载荷的映射关系，并在实验部分进行验证。3-RPS静力模型为

(1)

其中

式中J——雅可比矩阵

e——加载平台中心与分支距离

Fri——支架驱动力，i=1，2，3

Fci——支架约束力，i=1，2，3

在驱动力方向上(图3a)进行受力分析，易知有

Fr1=(Fla1+Fla2)/cosβ

式中β——支架倾斜角，取20°

Flai——驱动力方向载荷下支架两侧柔性移动副处的受力，i=1，2

在约束力方向上(图3b)有

式中 δv1——约束力作用下支架竖直方向变形量

δh1——约束力作用下支架水平方向变形量

δθv1——约束力作用下柔性移动副的转角

δθh1——约束力作用下支架上梁的转角

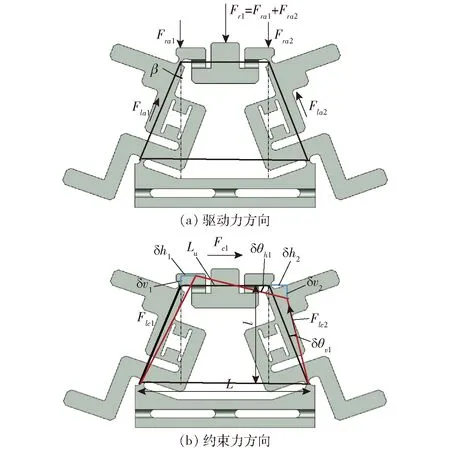
图3 传感器支架受力分析Fig.3 Force analyses of sensor bracket

由变形能等于载荷做功可得

(2)

式中Flci——约束力方向载荷下支架两侧柔性移动副处的受力

由支架对称性，可求出外载到6个测力分支Fli的力映射矩阵为

(3)

其中

3 柔性铰六维力传感器刚度模型

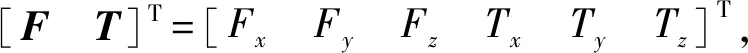
(4)

(5)

其中

(6)

式中Kp——分支刚度

kai、kci——第i分支对应的分支刚度

δr——各个分支沿对应力方向的变形量

有

(7)

其中

式中K——六维力传感器的刚度矩阵

图3a中，Fr方向上支架变形量主要来源于柔性移动副的变形，柔性移动副的变形量δe和标准拉压传感器处的变形量δs相等，则可以求出

(8)

图3b中，Fc方向上支架变形量为δh，由文献[17-19]可知，4个柔性转动副组成的平行四边形受力转动变形时，其转动刚度等效于一个柔性转动副的转动刚度，故可以推导出

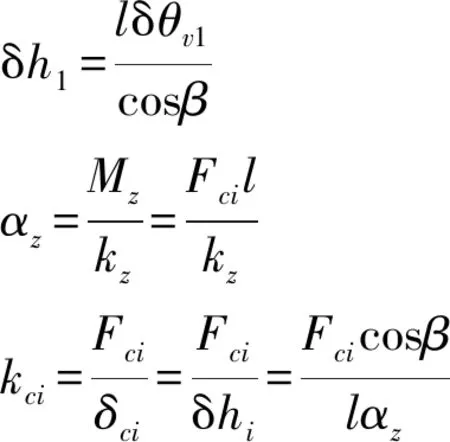
(9)

式中αz——等效柔性转动副受力产生的转角

kz——柔性转动副转动刚度

图4为平行四边形框架中的单边直圆柔性铰链，受力分析可得

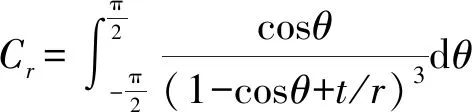
式中t——铰链最小厚度

tθ——柔性铰链微元长度

Cr——转动刚度系数r——铰链半径

φ——受力变形产生的角度

Tb——外载作用产生的弯矩

E——材料的弹性模量

h——弹性支架的厚度

对于支架的直圆柔性铰链，相当于两个单边直圆铰链，推导过程类似，只需改动Cr中系数即可，故有

(10)

对于由4个单边直圆柔性转动铰链组成的柔性等效移动副，其刚度为

(11)

式中g——柔性移动副长度

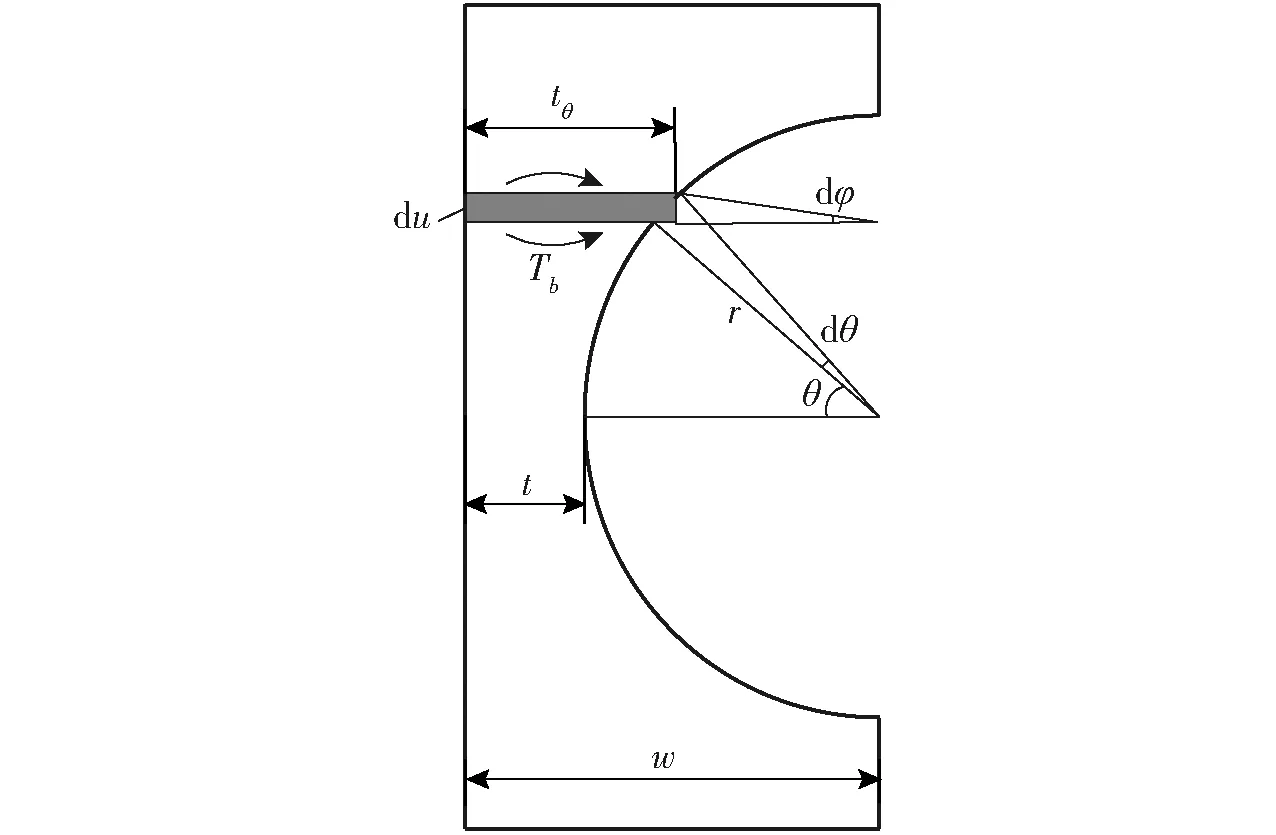
图4 柔性铰链转动刚度计算Fig.4 Rotational stiffness calculation of flexure hinge

建立六维力传感器的整体刚度模型之后，根据上述理论公式，代入模型中的具体数值r=1 mm,t=2 mm,e=90 mm,h=24 mm,g=10 mm,L=94 mm,l=59.2 mm,E=71.7，可求得：kai=1.028×108N/m,kci=2.355×106N/m。

传感器整体变形量与外载荷之间的关系可表示为

(12)

若分别在x、y、z方向施加单方向力，由式(12)可得到对应的传感器变形量，如表1所示。

有限元仿真结果如图5所示，分别在动平台上施加3个方向的载荷，这里取动平台中心节点变形量表示传感器的总体变形量。由图5a可知，传感器在x方向受力变形量为0.63 mm，比理论计算值0.51 mm稍大。其他方向变形量如表1所示。对比可知，仿真值与理论值基本吻合，从而验证了理论推导的正确性。理论变形量稍小是由于理论分析时将支架上厚度较大的部分视为刚体，忽略了该部分的变形量。

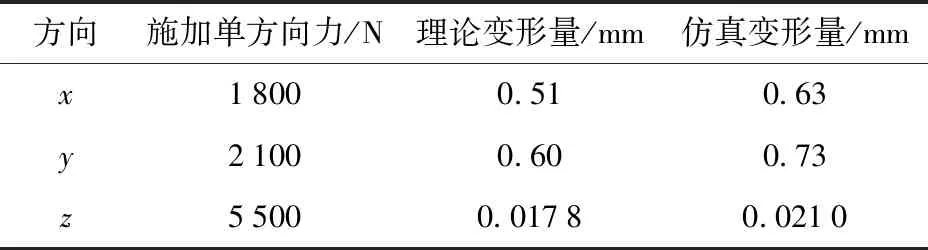
表1 3个方向加载力时理论与仿真变形量Tab.1 Theoretical and simulative deformation by forces in three directions

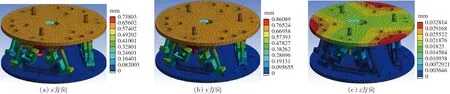
图5 3个方向加载变形Fig.5 Loading deformation in x, y and z directions

4 传感器结构优化设计

遗传算法(Genetic algorithm)是工程上常用的一种优化方法。由于其整体搜索策略和优化搜索方法在计算时不依赖于梯度信息或其他辅助知识，只需要影响搜索方向的目标函数和适应度函数，使得遗传算法不依赖于问题的具体领域，对问题的种类有很强的鲁棒性。解决优化问题可分为以下步骤：确定优化问题的数学模型、变量；明确约束条件和目标函数；选择合适优化算法，编写优化程序，得出问题的最优解。本文通过编程计算，得出各优化目标的参数化显式表达式，从而进行遗传算法优化。

(1)优化目标函数

目前从广义角度，六维力传感器的各向同性是国内外学者普遍认可和采用的评价指标。各向同性包含了灵敏度、刚度等，是指传感器在每个维度方向上性能的一致性。熊有伦[20]从信息矩阵的角度考虑，认为各向同性度好的传感器所提供的平均信息量最多，并提出以此准则确定传感器的结构参数。YAO等[21]使用一种新的分析方法，对Stewart六维力传感器各向同性进行了研究，得出各向同性最优时关于各结构参数的解析表达式。各向同性度越接近于1越好，因此根据力各向同性度和灵敏度各项同性度表达式，选择优化目标函数如下

(13)

(14)

(15)

(16)

可以看出，式(13)～(16)中，各优化函数与r、t、e等结构参数有关，矩阵G为传感器一阶静力影响系数矩阵，矩阵D为G的逆阵。μff、μfm、μsf、μsm分别表示力各向同性度、力矩各向同性度、力灵敏度各向同性度、力矩灵敏度各向同性度。另各向同性度综合优化目标函数为

fh=k1μff+k2μfm+k3μsf+k4μsm

(17)

式中ki——权重系数，i=1,2,3,4

优化过程中可根据需求，调整权重系数，使传感器综合性能满足优化目标。

(2)参数取值

传感器设计原则为空间尺寸与支架分布应尽可能紧凑；支架和标准拉压传感器框架尺寸应在上平台直径290 mm范围内；3个支架不能互相干涉；保证强度的同时减轻质量。受上述因素的限制，通过三维模型可以得出理论上各设计参数取值应满足

(3)优化结果

通过编写遗传算法优化程序，多次优化得到了各目标函数的优化结果和取得最优解时各结构参数的取值，如表2和表3所示。对于各向同性度综合优化，这里取4个权重系数均为0.25。

表2 结构参数优化结果Tab.2 Optimization result of structural parameters mm

表3 目标函数优化结果Tab.3 Optimization result of objective functions

由表3可知，在有效取值范围内，传感器的力矩各向同性度和力矩灵敏度各向同性度较好，可以取到最优值0.985 6。传感器的力各向同性度和力灵敏度各项同性度稍差，经优化可以提高。综合考虑4个优化目标，在权重参数均取0.25的条件下，确定了各向同性度综合最优时的结构参数。

针对力各向同性度和力灵敏度各向同性度偏低，本文对各结构参数对各向同性度的影响进行了研究。通过改变某一结构参数的取值范围，保持其他参数不变，可得力各向同性度在L=192 mm或l=30 mm时可以取到最优解1；力灵敏度各向同性度在L=200 mm或l=29 mm时可以取到最优解1。结果表明，4种各向同性度对参数L和l非常敏感，而改变其他参数对结果影响不大。在空间尺寸允许的条件下，设计时应尽量使L取200 mm左右，l取30 mm左右，这样可以显著提高力各向同性度和力灵敏度各向同性度。

5 传感器样机实验

根据优化结果，本文进行了传感器样机试制，样机设计参数为：Fx=Fy=±1 500 N，Fz=±4 000 N，Tx=Ty=±200 N·m，Tz=±300 N·m。本文对传感器进行了标定实验，z方向标定实验如图6所示。利用杠杆原理，将载荷加至4 053 N，6个测力单元的信号通过9针串口与计算机相连，在相关通信软件中设置通讯协议，计算机在线采集数据。由于加载时可能出现偏载，实验对6个测力单元的测量数值取平均值，其与理论值对比结果如图7所示，由此得到传感器该方向上的精度。满量程载荷下，6个测力单元实测平均值为260.2 N，4 053/6=675.5 N，可知弹性支架分担了675.5-260.2=415.3 N的力，占61.5%，可见该传感器实现了用小量程标准拉压传感器测大载荷的设计目标。优化结构参数后支架能够承担更多的载荷，同时可以选用更小量程的标准拉压传感器。

图6 z方向标定实验Fig.6 Loading experiment of sensor in z direction

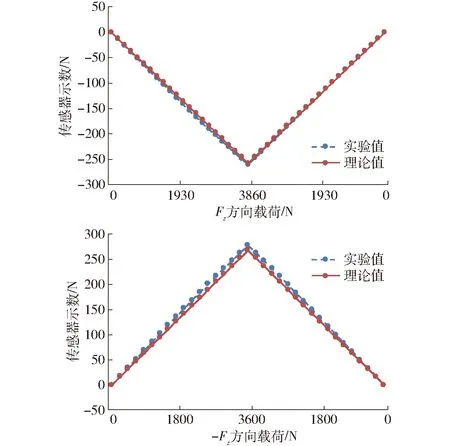
图7 z方向加载结果Fig.7 Loading result in z direction

其他方向测试与z方向类似，测试结果如表4所示。可见传感器在各方向精度较高，最大误差为1.05%，说明本文建立的静力模型是正确的。

表4 传感器测量精度Tab.4 Measurement accuracy of sensor %

为了验证传感器换件后无需二次标定，将传感器整体放置在3-SPR并联机械臂上，并在传感器测力平台安装了3个手爪，模仿机器人手臂的工作状态，如图8所示。调试控制并联机械臂的程序，进行测量实验。手爪抓取一个未知质量的沙桶，读取6个测力单元的示数，通过理论静力模型，换算出沙桶的理论质量。再用标准秤称出沙桶的实际质量，两者可得传感器主要受力方向的测量精度。

图8 传感器工况模拟实验Fig.8 Working condition experiment of sensor

实验经过多次测量取平均值，由数据建立的静力模型，可以计算出测力平台所受外载为[-0.52 N 0.9 N -65.91 N -0.58 N·m 0.2 N·m

-0.09 N·m]，其中主要受力Fz为-65.91 N。用标准秤测量未知沙桶的质量为6.8 kg，由此可知测量误差在0.38%以内，传感器更换测力单元无需进行二次标定即可快速投入使用，节省了现场标定的时间。

6 结论

(1)利用并联机构的优点和测力支架载荷分流的思想，设计了一种无间隙、承载能力强的柔性铰六维力传感器，采用等效法和微元法建立了传感器的理论模型，简化了计算过程，并利用有限元仿真验证了理论模型的正确性。

(2)采用遗传算法对传感器支架结构进行了优化，并根据优化结果进行了样机试制与实验。实验结果表明，样机具有使载荷分流的特性，能够实现在线快速换件使用，精确测量未知外载的6个分量，最大测量误差为1.05%。