可见光散射模型双向反射分布函数的仿真分析*

刘 燕，张 健，吕 瑛

（西北工业大学明德学院信息工程学院，西安710124）

1 引 言

20 世纪80年代以来，人类航天活动日益频繁，进入空间的目标数量不断增加，其载荷的复杂化、目标形状的多样化、目标体积的小型化对空间目标特性的研究提出了迫切的需要。目标与背景所能暴露呈现的特性是对可探测和可识别的参量的科学描述。对于空间目标而言，在所有空间目标监测与识别跟踪的相关任务中，希望尽可能详细地获得几何结构与尺寸、运行轨道、辐照度、辐亮度、偏振度、偏振角等特性数据。因为目标的几何机构与尺寸反映了目标的大小和基本结构特性，辐亮度反映了目标在特定轨道、特定位置和特定光照条件下的亮度信息，目标的偏振特性可以补充光度和光谱信息，有效提高对空间目标的识别能力[1-4]。

双向反射分布函数BRDF 模型是空间目标辐照度、辐亮度、偏振度、偏振角模型的重要组成部分。通过分析BRDF 模型随各参数的变化规律，可以有效地为研究空间目标特性提供基础。故此，主要针对可见光波段Torrance-Sparrow BRDF 模型随入射角、反射角及粗糙度的变化规律进行模拟并做出分析。

2 可见光散射模型

2.1 双向反射分布函数

BRDF 模型给出了物体表面光散射的空间分布。BRDF 的基本概念和物理意义见参考文献[1]。如图 1所示为 BRDF 的几何关系。其中，θi、φi表示入射光的天顶角和方位角；θr、φr表示探测光的天顶角和方位角。

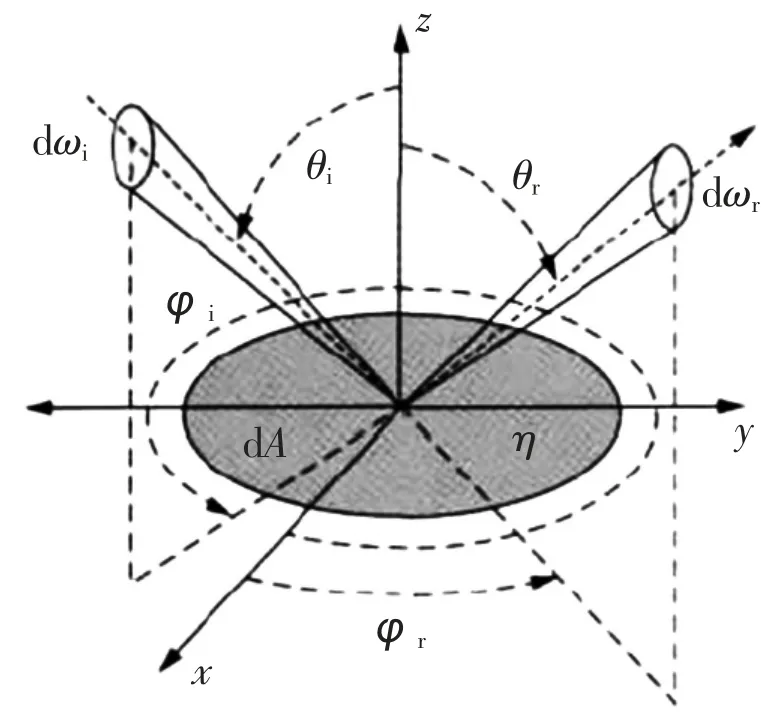
图1 BRDF 几何关系图

BRDF 的一般定义下式所示：

其取值范围为零到无限大，单位sr-1，它是一个微分量，不能直接测得。

BRDF 模型主要分为经验模型、物理模型和数据模型三大类。经验模型提供简洁的公式，便于快速计算，但它不考虑材质，也不一定满足物理定律，仅仅是提供一个反射光的近似；物理模型通常建立在被称为表面粗糙度的细节几何结构上，通过包含材料的各种几何及光学性质来尽可能精确近似现实中的材料；数据模型通常度量一个大的材料几何的BRDF，然后通过降维方法计算一个低维模型[5]。

2.2 T-S双向反射分布函数

BRDF 与物体表面法线z 及微面元法线zμ之间的相对位置关系如图2所示。以此构建Torrance-Sparrow（简称T-S）BRDF 模型，其表达式如下：

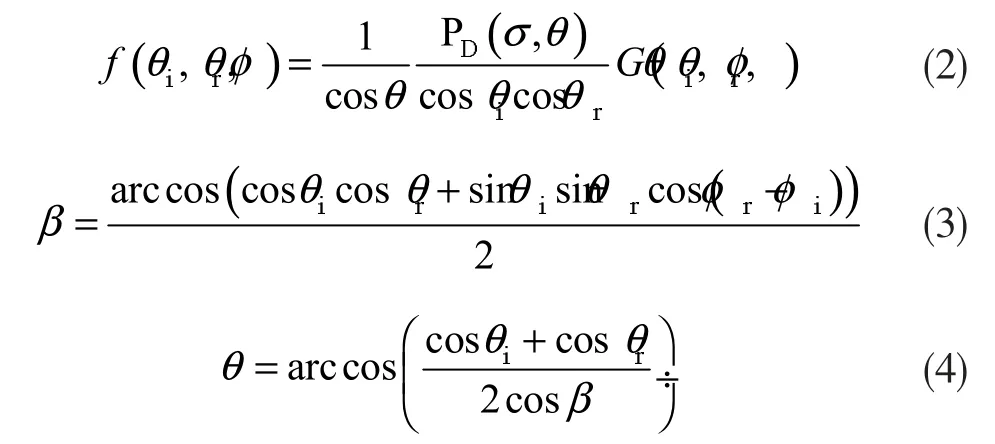
式(2)中，σ 表示物体材料表面的粗糙度，PD(σ,θ)为微面元法向概率分布函数，G(θi,θr,φ)为遮蔽因子，φ=φr-φi为方位角的差值；式(3)中，β 为入射方向与 zμ间的夹角；式(4)中，θ 为 z 与 zμ间的夹角，即图2 中的θN。以上模型的物理意义及基本理论可参见文献[6-7]。

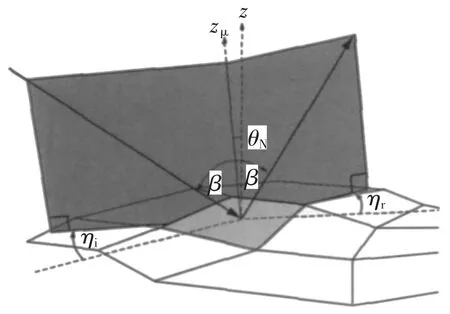
图2 微面元几何分布图

BRDF 的微面元概率分布函数如下式所示[8]：

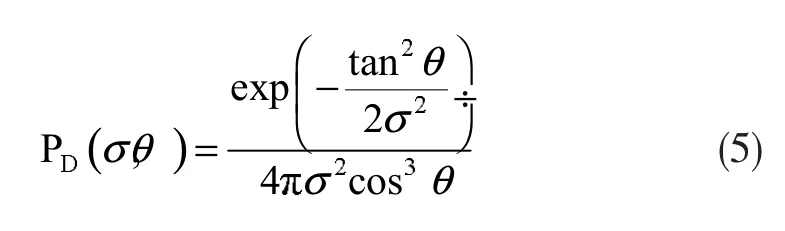
遮蔽因子 G(θi,θr,φ)可由如下公式表示[8]：

3 仿真分析

设置观测角θr=30°，方位角φ=180°，观察T-S模型在粗糙度 σ 分别为 0.1、0.2、0.3 时，BRDF 值随入射角θi的变化规律。模拟得到的曲线如图3所示。

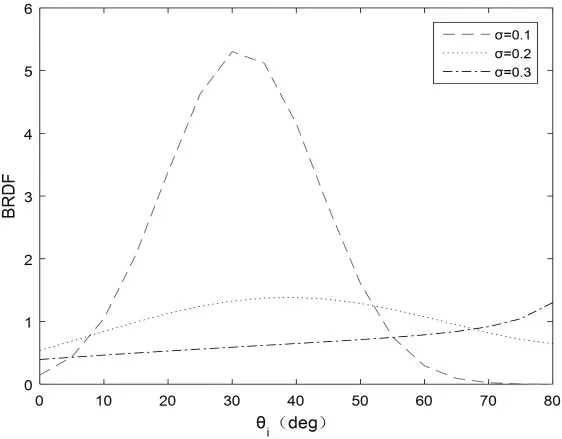
图3 BRDF 模拟结果（θr=30°条件下）

从图中可以看出在粗糙度较小，即σ=0.1 时，在观测角30°附近BRDF 出现极大值。这是因为粗糙度很小的微面表面反射近似为镜面反射，根据反射定律得出在同一平面相同反射角处出现极大值，结果正确。但是，随着粗糙度的增大，漫反射分量增加，镜面反射削弱，可以看到在 σ=0.2 时，θi=30°附近依然出现较弱的极大值，但在σ=0.3 时，BRDF 没有极大值出现，而是随着入射角的增大而增大，说明镜面反射已经几乎不存在，微面表面主要以漫反射为主。

设置观测角θr=60°，方位角φ=180°，观察T-S模型在粗糙度 σ 分别为 0.1、0.2、0.3 时，BRDF 值随入射角θi的变化规律，模拟得到的曲线如图4所示。

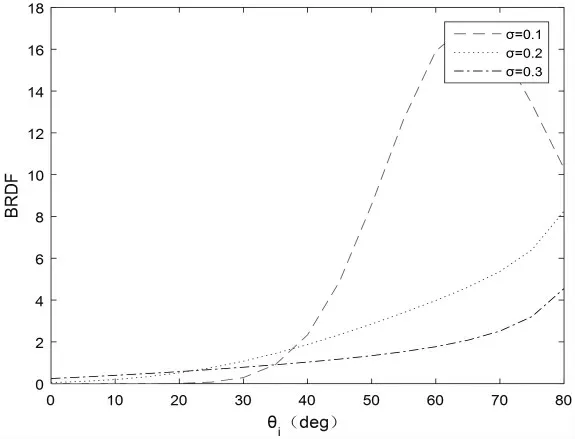
图4 BRDF模拟结果（θr=60°条件下）

从图4 可见，粗糙度较小即σ=0.1 时，在观测角60°附近BRDF 出现极大值，然而在σ=0.2 时，BRDF 却没有极大值出现，而是随着入射角的增大而增大。通过与图3 对比，可以发现观测角的增大会增加BRDF 中的漫反射分量，从而削弱镜面反射的作用。

4 结束语

对可见光波段描述目标表面散射特性的双向反射分布函数进行模拟，并重点分析了基于微面元理论的T-S BRDF 值随入射角、观测角和粗糙度的变化规律，从而得出BRDF 主要与目标的材料，观测位置，光源位置等因素有关。在此基础上，便可在后续的研究工作中使用已有的BRDF 模型与菲涅耳反射穆勒矩阵相互作用，得到偏振双向反射分布函数模型，以分析空间目标的偏振特性。