改进和声搜索的智能RGV动态调度策略研究*

于红斌，周康垒，李俊霖

（河南师范大学计算机与信息工程学院,河南新乡453007）

1 引 言

随着先进制造技术的发展，一个工厂的业绩与效率很大程度上取决于加工设备的智能化程度，智能加工系统已然成为现代化工厂的代名词。有轨制导车辆RGV（Rail Guided Vehicle）作为一种无人驾驶、能在固定轨道上自由运行的智能车，可以根据指令自动控制移动方向和距离完成上下料及清洗物料等作业任务。智能RGV 调度问题属于单处理机作业调度的多目标规划问题，目的是要制定一种优化作业调度策略，旨在使系统效率达到最优。分析智能RGV 调度问题的相关文献，大多数算法仅是单一指标优化问题[1-5]，在实际问题中，往往很难找到一种调度策略适用于所有的情况，因此在解决相关问题时，要结合问题制定适合的调度策略，且不能仅考虑其中一个因素而忽略其它因素，必须要全方位考虑才能使系统的作业效率达到最高。故此，从一个实际的生产实例出发，研究多指标RGV 调度问题，建立包含CNC 等待时间与RGV 调度运行时间的多目标函数，进而提出一种改进的和声搜索（Improved Harmony Search,IHS）算法来求解目标函数的最优可行解，以解决智能RGV 的调度问题。

2 基于IHS的调度模型

和声搜索算法(Harmony Search,HS)是一种新的群智能优化算法[6-7]，它通过调节每一维的变量来寻找近似最优解。但主要应用于连续优化区域，存在寻优精度低、早熟收敛和对离散问题求解效果不佳等缺点。

与传统的连续优化HS 不同，改进算法采用离散优化策略，结合RGV 问题，通过动态的参数选择微调RGV 调度策略，计算该RGV 调度策略相对应的各目标函数，动态替换和声记忆库（HarmonyMemory,HM）中最差的调度策略。其算法流程图如图1。

图1 改进的和声搜索算法流程图

3 基于IHS的智能RGV动态调度

3.1 智能RGV系统构成

以2018 中国工业与应用数学协会全国大学生数学建模竞赛B 题[8]所给出的数据为例，设定一种智能加工系统，由8 台计算机数控机床（CNC）、1 辆轨道式自动引导车（RGV）、1 条RGV 直线轨道、1条上料传送带、1 条下料传送带等附属设备组成，如图2所示。

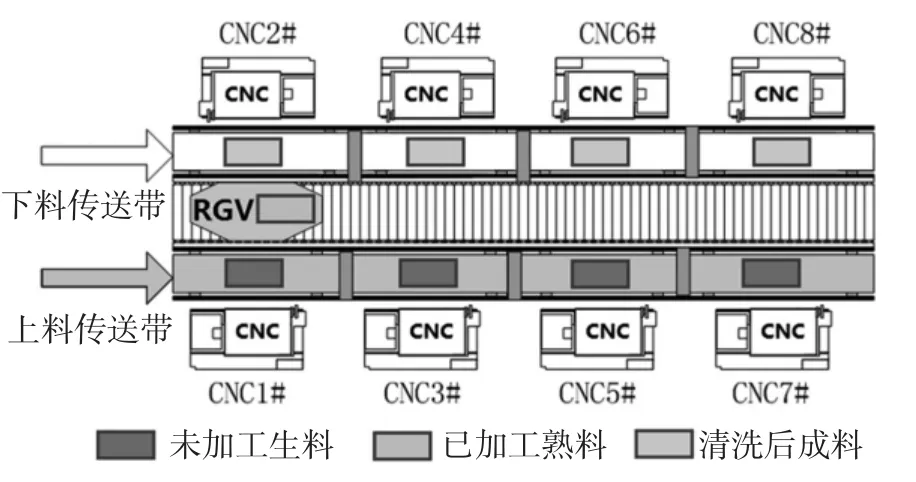
图2 智能加工系统

3.2 智能RGV系统模型

3.2.1 优化目标函数

对于不同工序的物料加工，要使系统的工作效率尽可能高，则需要考虑CNC 的等待时间和RGV的移动距离所用时间这两个主要因素。建立的数学模型如下:

目标函数式(1)的意义是：CNC 等待时间的标准差与RGV 移动距离所有时间之和的最小化。X=(x1,x2,...,xn)是一组可行解，表示CNC 加工物料的序列；ww11、ww22分别为 f1、f2的权重；f1表示可行解 X所对应的CNC 的等待时间标准差；f2表示RGV 移动距离所用的时间，有如下式：

其中，twait(xi)表示编号为 xi的CNC 从发出请求到受到响应所等待的时间；Taver表示CNC 发出请求到响应上下料的平均等待时间。

3.2.2 时间模型

为了增加模型的可靠性，CNC 等待时间采用递归算法计算、RGV 移动时间使用蒙特卡洛算法计算，如下式：

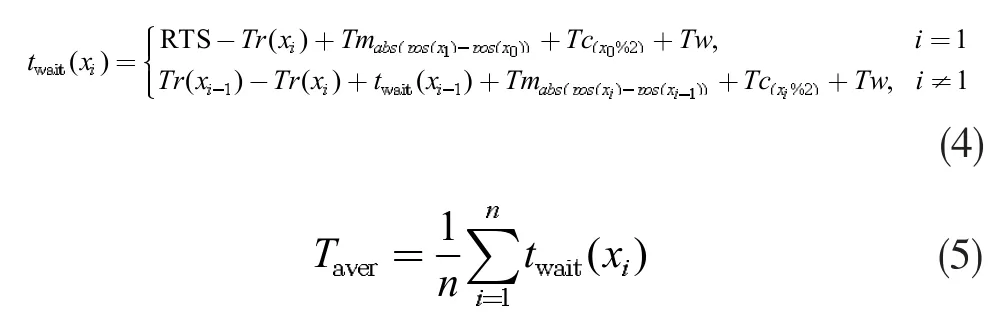
式（5）中，RTS 表示系统启动作业前所需要检测机器是否能正常工作的自检时间，在此设置系统开机自检时间以确保所有CNC 都能得到有效检测，从而降低系统发生故障的概率；pos(xi)表示编号为xi的CNC在RGV 直线轨道上的位置，pos(xo)表示系统初始化状态RGV所处的轨道位置（对于本改进智能加工系统，规定从RGV 轨道的左侧开始依次编号，分别为1、2、3、4）；Tm 表示 RGV 由前一次响应位置移动到下一次响应位置所需的时间，Tmi表示移动i 个单位距离所需要的时间；Tc 表示为奇数编号的CNC 上下料所用的时间；TTww 表示RGV 清洗物料所用的时间；Tr 表示CNC 请求的时刻（包括空闲请求和加工完成的请求）。

3.2.3 模型评价指标

定义系统效率为加工一个物料所需的最短时间与实际加工的平均加工时间之比，以此作为评价系统性能的重要指标，如下式：

其中，实际加工一个物料所需要的时间包括CNC 的平均等待时间、RGV 的平均移动时间、加工一个物料所需要的时间以及上下料、清洗所用的时间。由于在对不同的CNC 上下料所用的时间不同，因此取二者的平均值Tcaver作为系统效率的计算。

4 实验结果与分析

采用IHS 算法对上述初始化的模型优化求解设置适应一道工序加工情况下的模型参数：RTS=500s，ww11=ww22=0.5，在智能加工系统优化模型中，第i个物料加工的下料时刻等于编号为xi的CNC 的第i 次请求时刻Tr(xi)与一道工序物料加工所用的时间tfinish1之差，如下式所示：

在同一台CNC 上，前一物料的下料时间即为下一物料的上料时间，即为：

这里，i 和j 分别为在同一台CNC 上加工的相邻两个物料的编号。

将赛题所给第1 组测试数据数据作为系统参数，采用改进的和声搜索算法计算RGV 为CNC 上料、下料的具体时刻，如表1所示。

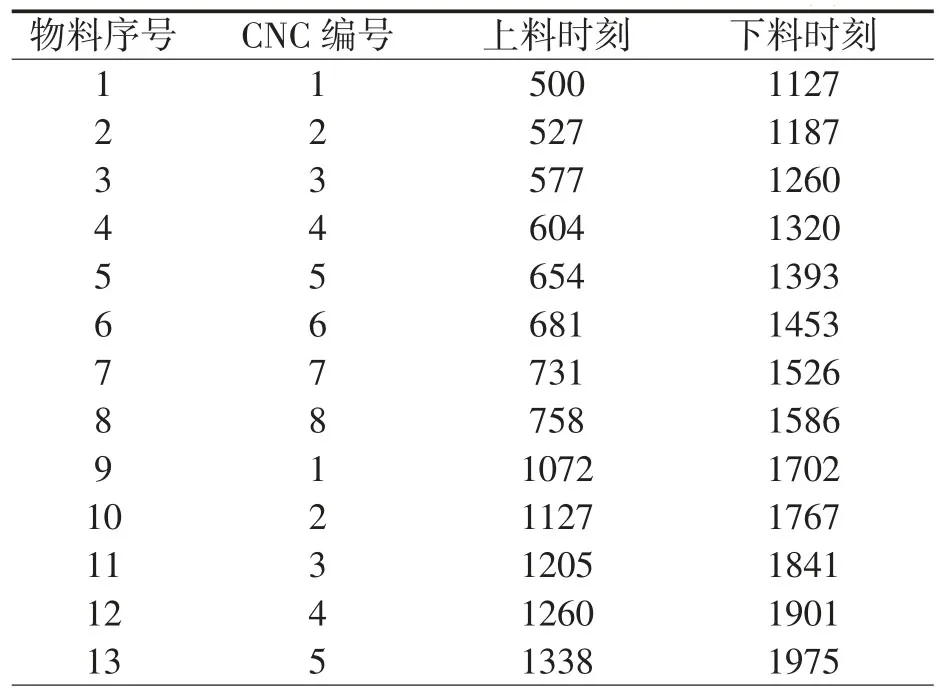
表1 3000 秒内系统作业具体分布（第1 组）单位：秒

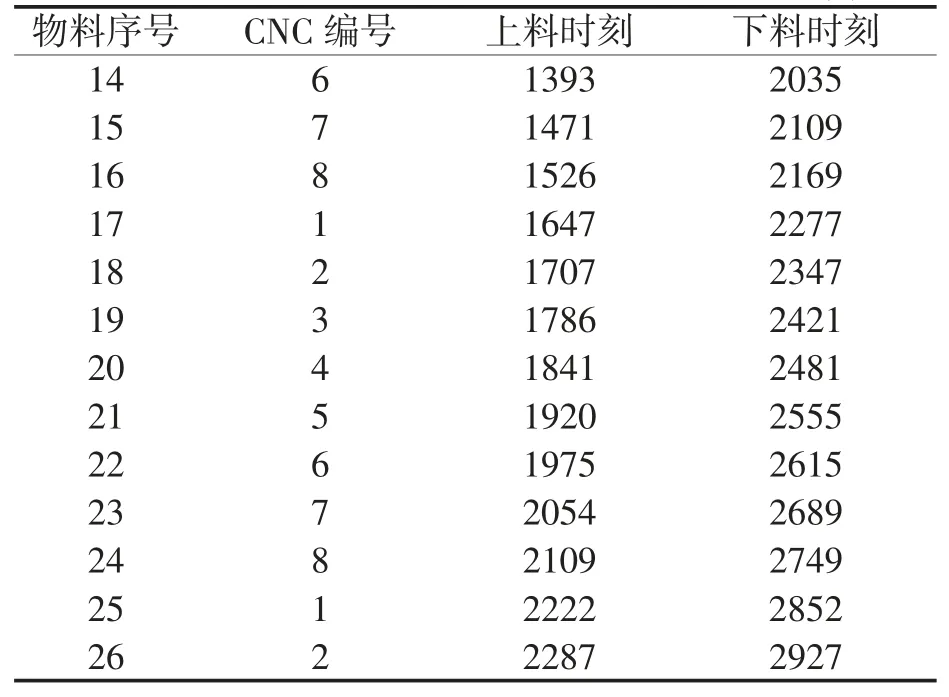
续表 单位：秒

其中，上料时刻和下料时刻分别为上料和下料的开始时间，以秒为单位。在一个作业班次内，系统开始启动的时刻即为0 时刻。

系统在一个作业班次内三组测试数据结果对比如表2所示。

表2 一道工序的物料加工相关参数

由表2 可知，随着参数的变动，系统作业效率均在95%左右且相差无几，因此说明使用改进的IHS算法对RGV 进行动态调度的效率高，算法性能稳定。该算法的复杂度为O(nlnn)，对于高速而言，该算法运行的时间可以忽略不计。

5 结束语

对和声搜索算法进行了改进，使之适用于离散优化模型。结合RGV 问题，提出多目标优化的离散策略，提高算法的局部搜索性能，实验结果表明相比于标准和声搜索算法，改进算法性能稳定。对于多道工序物料加工以及发生系统故障等情况，验证算法的性能是今后要进一步开展的工作。