基于全膛烧蚀磨损特征的火炮内弹道仿真研究

金文奇， 宁金贵， 王剑， 邓波

(63850部队， 吉林 白城 137000)

0 引言

烧蚀磨损是火炮弹道性能退化的根本原因，烧蚀内弹道仿真是获取火炮烧蚀磨损后的内弹道性能以及膛内特征点诸元的重要手段，可以为火炮身管寿命设计、身管寿命状态评判或预测提供重要支撑，因此高精度的火炮烧蚀内弹道仿真成为火炮业内研究的一个重点方向。目前，内弹道仿真研究主要立足于经典内弹道理论，在发射药燃烧规律、弹丸起动压力、火炮内膛结构等差异方面开展研究。张喜发等[1]建立了弹丸起动压力方程与火炮坡膛结构、弹带属性(结构、尺寸、材质等)和起始部膛线剩余高度的函数关系，取代了经典内弹道学的估算法，用以确定弹丸起动压力，提供一种烧蚀火炮内弹道仿真方法(简称张氏烧蚀内弹道方法)。米粮川等[2]以弹丸起动压力稳定性为研究对象，利用计算机技术和高塑性有限元理论对弹带挤进坡膛过程进行数值仿真研究，得出起动压力受坡膛角影响较大的结论。孙河洋等[3]研究了不同坡膛结构对弹带挤进过程受力影响，指出坡膛结构及弹带应力状态对火炮内弹道性能的影响。刘双杰等[4]利用某钝感发射药的燃烧规律建立了某型火炮的内弹道模型，得出钝感剂含量的微小增量就会引起膛压急剧升高的结论。刘林等[5]建立了基于混合装药经典内弹道的某榴弹炮内弹道Simulink仿真模型，并进行了内弹道参数符合计算，结果表明平均相对误差及各单项误差均可满足工程实际要求。王加刚等[6]建立了基于埋头弹两次点火及火药燃烧控制技术的内弹道理论模型，分析了主装药药量、弹丸质量、药室容积、火药力等参数变化对内弹道性能的影响。Lu等[7]进行了埋头弹火炮药室推进剂点火燃烧的实验研究与数值模拟。Liu等[8]建立了燃烧轻气炮内弹道双区准维燃烧模型，数值模拟了燃烧轻气炮氢- 氧预混气体低温高压装填条件下的内弹道过程。

综上所述可知，只有文献[1]研究了烧蚀炮膛对内弹道性能的影响，但未考虑烧蚀磨损引起的药室容积增大、变炮膛截面积、弹后容积增量等因素对火炮内弹道性能的影响。为提高烧蚀火炮内弹道诸元仿真精度，精确预测烧蚀火炮内弹道诸元和剩余身管寿命，指导火炮研制、使用和试验鉴定，本文提出一种基于全膛烧蚀磨损特征的火炮内弹道仿真方法。

1 基于全膛烧蚀磨损特征的内弹道仿真

1.1 烧蚀火炮内弹道结构特点

烧蚀火炮与新炮内弹道结构如图1所示。

设新炮弹后火药气体自由容积为W，W=Wψ+Sl，Wψ为药室火药气体自由容积，S为新炮膛截面积，S=πd2/4；烧蚀火炮弹后火药气体自由容积为W′，W′=Wψa+W(l)，Wψa为烧蚀药室火药气体自由容积，W(l)为弹丸行程l时增加的弹后容积，W(l)=Sl+ΔW(l)，ΔW(l)为弹后烧蚀容积增量；S′(l)为烧蚀炮膛任一截面积，S′(l)=π(d+Δd(l))2/4，Δd(l)为对应的烧蚀等效内径增量(后文简写为Δd)。由此可知，烧蚀火炮与新炮的内弹道性能参数存在以下变化：弹后火药气体自由容积由Wψ+Sl增大为Wψa+Sl+ΔW(l)、火药气体作用于弹底的有效面积由等截面积S增大为变截面积S′(l)、弹丸起动压力因烧蚀磨损变小。

烧蚀火炮炮膛截面积S′(l)和弹后烧蚀容积增量ΔW(l)可采用注液和测径两种方式测量。

1.1.1 注液式测量

注液式炮膛截面积测量方式如图2所示。

测量时，首先通过漏斗向药室密封的垂直炮管内注入体积为Δw0的测量液(Δw0应满足浮块下底面与弹丸运动起始位置齐平)，记录标尺初始读数l0；然后逐次向垂直炮管注入适量体积的测量液Δwi(i=1,2,…,n1，i为截面顺序数，n1为身管总截面数)，记录对应的标尺读数li；依据如下公式计算距密封塞上表面l(l=li-l0)处的炮膛截面积S′(l)和弹后烧蚀容积增量ΔW(l):

(1)

(2)

(3)

式中：j为弹丸行程l对应的圆台数。

1.1.2 测径式测量

采用传统测内径方法，按步长100 mm从膛线起始部至炮口测量烧蚀炮膛同一截面多个方向(至少水平和垂直两个方向)的内径，用均值作为炮膛等效圆截面直径。假定弹丸行程l处的等效圆截面直径为d+Δd，则炮膛截面积S′(l)=π(d+Δd)2/4，烧蚀等效直径增量Δd. 在计算ΔW(l)时，可将烧蚀炮膛看成由沿炮膛轴线从膛线起始部至炮口的n1-1个不同参数等效圆台组成，设任意圆台上底直径为di(di=d+Δdi)、下底直径为di-1(di-1=d+Δdi-1)、高为h，则弹丸行程l(对应第j个圆台的上底)时增加的弹后容积W(l)可用(4)式表示：

(4)

(5)

则弹后烧蚀容积增量ΔW(l)可表示为

(6)

1.2 内弹道模型

经典内弹道模型[9-12]由(7)式～(10)式组成。

几何燃烧定律：

ψ=χZ+χλZ2,

(7)

式中：ψ为火药已燃百分数；χ、λ为火药形状特征量；Z为火药已燃相对厚度。

燃速定律：

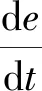
(8)

式中：e为药粒已燃厚度；u1为燃速系数；p为炮膛压力。

弹丸运动方程：

Spdt=φmdv,

(9)

式中：φ为次要功计算系数；m为弹丸质量；v为弹丸运动速度。

内弹道学基本方程：

(10)

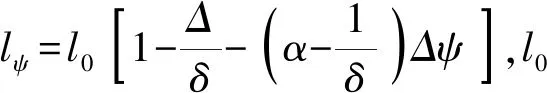
火炮烧蚀后，致使内弹道模型中的弹丸起动压力、弹丸运动方程和内弹道基本方程改变，下面分别叙述。

烧蚀火炮的弹丸起动压力[1]：

(11)

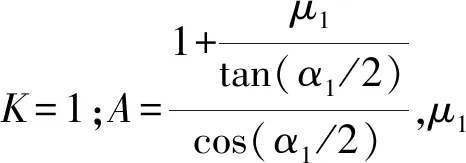
将S′(l)=π(d+Δd)2/4展开，并用S、d和Δd表示为

(12)

由于Δd较小，工程计算时可略去(12)式中的第3项，则烧蚀炮膛截面积可表示为

S′(l)≈S(1+2Δd/d).

(13)

将W′=Wψa+Sl+ΔW(l)变换为

W′=S(lψa+l+lΔd).

(14)

对于已燃火药ψ、弹丸行程l、炮膛截面积S′(l)、弹后空间增加体积为W(l)的火炮，此时弹丸运动动力变为pS′(l)，火药气体残存势能pW变为pW′，即由Sp(lψ+l)变换为Sp(lψa+l+lΔd)，则(9)式、(10)式变换为

(15)

(16)

对于(16)式中的lΔd可用β1=lΔd/l表示，则(16)式变换为

式中：β1为烧蚀磨损容积增量相对缩径长。

几何燃烧定律选取三项式的形状函数，燃速定律选取指数函数，建立基于全膛烧蚀磨损特征的烧蚀火炮内弹道模型如下：

(17)

式中：μ为火药形状特征量；e1为弧厚；Ik为火药燃烧结束瞬间的燃烧全冲量。

1.3 减面燃烧火药的分析解

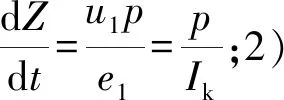
1.3.1 前期结束时

由于l=0、v=0、弹丸起动压力p0已由(11)式确定，根据定容状态方程，求得火药已燃百分数ψ0、火药相对表面积σ0和火药燃去的相对厚度Z0：

(18)

1.3.2 第一时期

借鉴经典内弹道学第一时期弹道诸元求解方法，将(17)式中的方程2和方程3联立，消去pdt,即得

(19)

对(19)式积分，从起始条件v=0、Z=Z0到任一瞬间v、Z，由于火药已燃相对厚度Z与初始火药已燃厚度Z0的差x=Z-Z0，则有

(20)

将Z=x+Z0代入(17)式中的(1)式，并令K1=χσ0，从而导出

ψ=ψ0+K1x+χλx2.

(21)

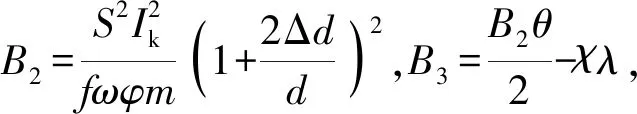
(22)

为了导出l的表达式，对(22)式两边积分：

(23)

(24)

将(20)式、(21)式代入(17)式中的方程5，并整理得，压力函数：

(25)

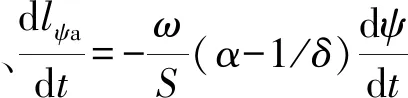
(26)

(27)

式中：σm、vm、β1m分别为最大膛压时对应的火药相对表面积、弹丸速度、烧蚀磨损容积增量相对缩径长，δ1=1/(α-1/δ)。(27)式即为最大膛压条件方程。

(28)

(28)式为最大膛压条件的另一种表达式，要确定xm必须预先已知pmax，而pmax又正是所求的值，此外pmax必然出现在xm～1-Z0之间。因此只能采用逐次逼近法。其原理如下：

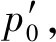
3) 对于情况①，迭代终止时的p(r)即为最大膛压pmax；对于情况②，最大膛压pmax必定出现在x(r-1)～x(r)之间，以x2=(x(r-1)+x(r))/2代替x，计算对应的v、ψ、l和p，若p-p(r-1)≤Δp或p-p(r)≤Δp，则取p作为pmax的近似值，否则进行下一轮迭代；

4) 令h1=(x(r)-x(r-1))/m1，按步骤2进行迭代，若出现y(r-1)>0、y(r)=0，则p(r)则为pmax；若出现y(r-1)>0、y(r)<0，则以x2=(x(r-1)+x(r))/2代替x，计算对应的v、ψ、l和p，取p作为pmax的近似值。

通常m1取300～500之间的整数，第一轮迭代就能获得满足精度要求的最大膛压。

1.3.3 燃烧结束时

将火药燃烧结束瞬间的条件：Z=1，x=xk=1-Z0(xk为火药燃烧结束时已燃相对厚度Z与初始火药已燃厚度Z0的差)、ψ=1代入(20)式、(24)式和(25)式，即得vk、lk和pk的表达式为

(29)

式中：下标k代表火药燃烧结束标志；l1a为火药燃烧完时的烧蚀药室自由容积缩径长。

1.3.4 第二时期

火药已燃烧完，内弹道模型变为

(30)

将(30)式中方程1、方程2联立并消去Sp，得到

(31)

(32)

对(32)式导出以l为函数的速度方程:

(33)

由(30)式方程2，得

(34)

将燃烧结束时压力表示为

(35)

(36)

将(33)式和(35)式中的l替换为弹丸全行程lg，则得炮口速度和膛压为

(37)

由第一时期和第二时期膛压p、弹丸速度v的解析解，可得到烧蚀火炮整个内弹道时期的p-l和v-l曲线。

1.3.5 各时期时间曲线的计算

式中：t′取0～l′之间速度的平均值，即t′=2l′/v′，v′为l′对应的速度。为减小误差，通常取尽可能小的l′值。

1.4 内弹道数值解

用多孔火药的形状函数和燃速定律替代方程组(17)式中的方程1和方程2，即得到多孔火药基于全膛烧蚀磨损特征的内弹道模型：

(38)

(39)

(39)式为1阶微分方程组，要求解内弹道性能，通常采用4阶龙格- 库塔法[9，14-15]。其方法如下：

对于1阶微分方程组

式中：q为因变量顺序数，q=1，2，…，Q，Q为因变量个数；yq为z的第q个因变量；yq0为z=z0时的初值。

上述微分方程组的解：

式中：k为自变量x的离散点个数；步长h2=zk+1-zk；

2 算例

采用1.4节建立的烧蚀内弹道无量纲微分方程组(39)式，用4阶龙格- 库塔法编程对某高射炮射击前后的内弹道进行仿真计算。

2.1 试验数据

某高射炮内弹道计算所需参数如表1所示。射击验证前初速为988.3 m/s，射弹1 145发后，初速为902.2 m/s，射击后烧蚀磨损量Δd如表2所示，烧蚀磨损容积增量缩径长lΔd如表3所示。

依据表2数据得到Δd的示意图，如图3所示。

磨损量Δd的拟合函数：

依据表3数据得到lΔd的示意图如图4所示。

表1 内弹道计算所需参数

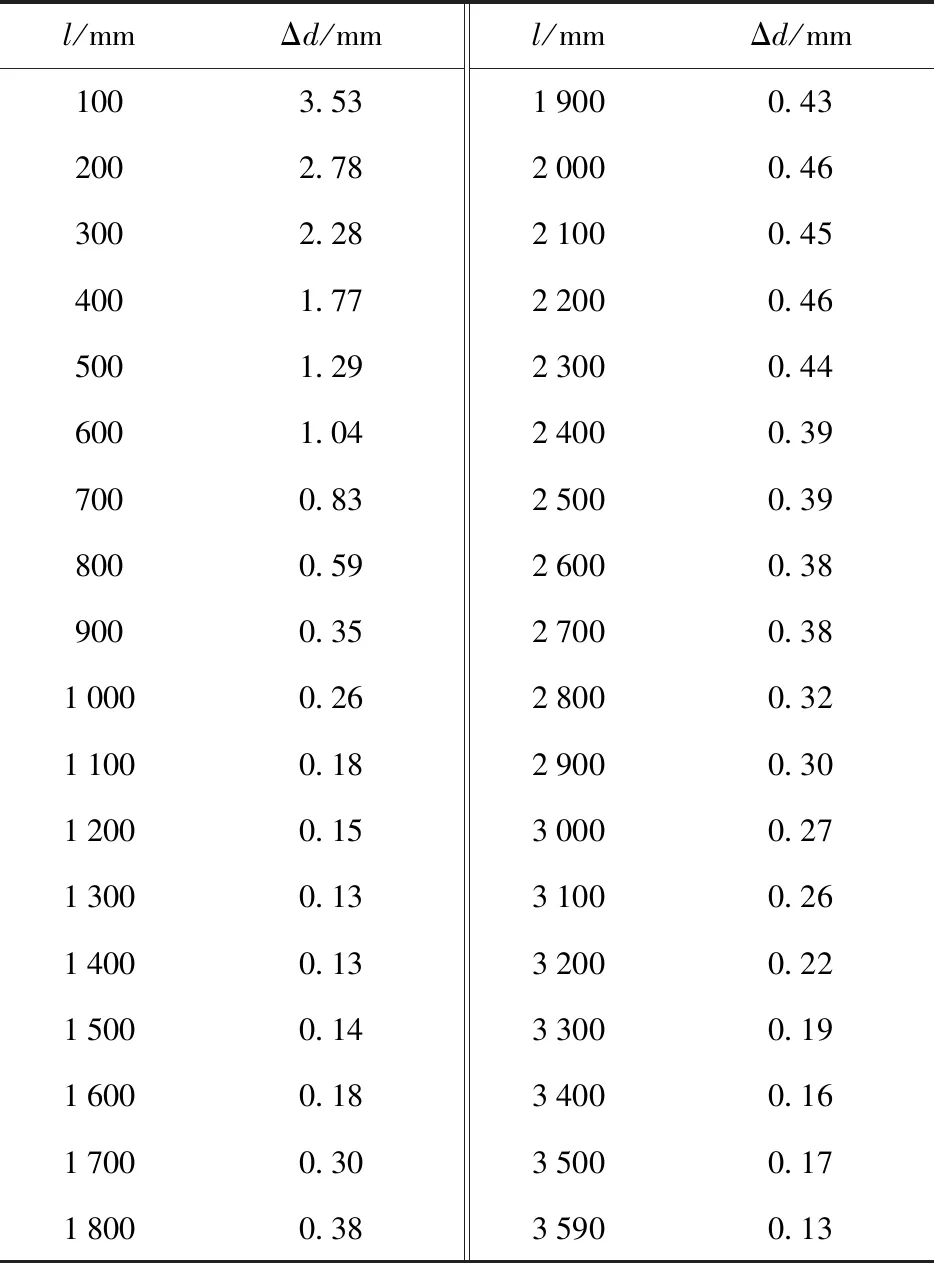
表2 射击后烧蚀磨损量

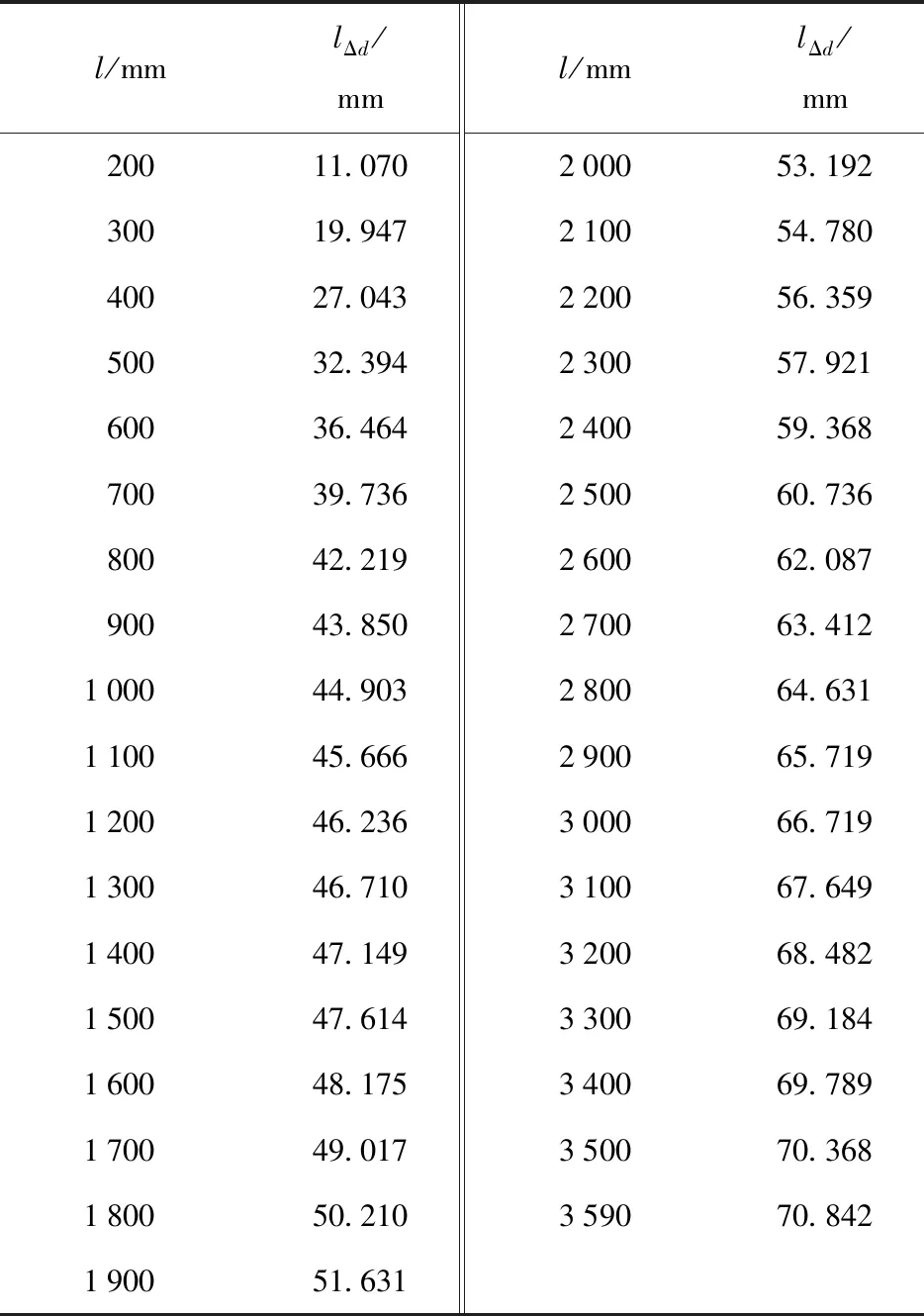
表3 烧蚀磨损容积增量缩径长

磨损缩径长lΔd拟合函数：

2.2 初始条件

lΔd=0.070 8 m，p0=12.4 MPa，ψ0=8.6×10-3，Z0=0.011 5，Ik=9.32×10-5,B=2.169,Δ=7.682×102，ρ=2.439×10-4，Zk=1.443.

2.3 仿真计算结果

将内弹道计算结果绘制成p-t、v-t、p-l、v-l曲线，如图5～图8所示。

从图5～图8可以看出：1)相同弹药条件下，射击验证前的最大膛压大于射击磨损后最大膛压，且最大值出现时机向炮口方向移动；2)相同弹药条件下，射击验证前的初速大于射击磨损后初速；3)射击磨损后，只考虑弹丸起动压力的最大膛压、初速大于考虑弹丸起动压力和全膛烧蚀磨损的最大膛压和初速。

射击验证前与磨损后实测值和仿真值结果如表4所示。

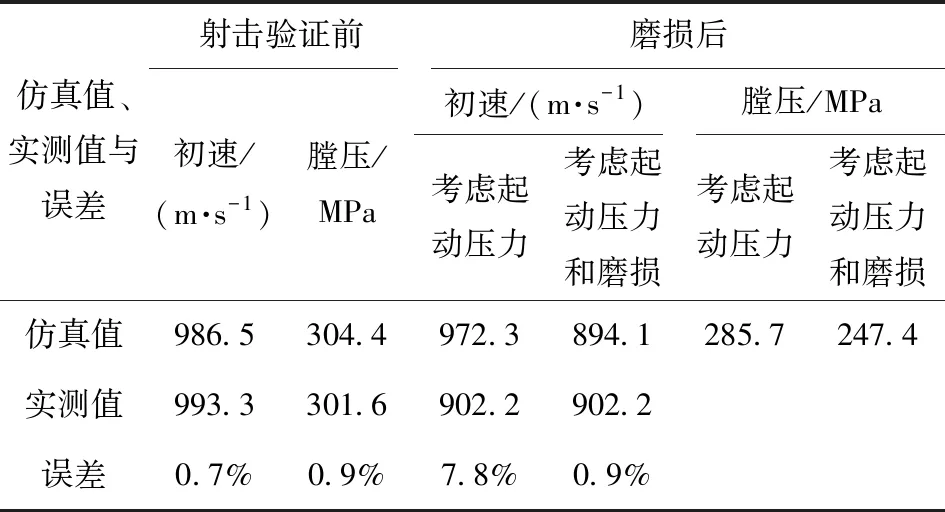
表4 射击验证前与磨损后实测值和仿真值

从图5～图8和表4可知：1)基于全膛烧蚀磨损的内弹道仿真值与试验值符合较好，初速误差为0.9%，能够满足火炮工程实践3%仿真误差要求；2)只考虑弹丸起动压力的内弹道仿真值比考虑全膛烧蚀磨损和弹丸起动压力的仿真值误差大。

3 结论

本文对火炮烧蚀磨损后内弹道性能变化规律进行了仿真研究。通过分析和计算建立了体现全膛烧蚀的弹丸运动方程和内弹道基本方程，从而建立基于全膛烧蚀的内弹道模型，并导出了相应的内弹道解算方法。以某火炮试验数据为例进行仿真计算，结果表明能够满足火炮工程实践的仿真误差要求。主要贡献及所得结论如下：

1) 引入了烧蚀磨损容积增量缩径长，建立了基于全膛烧蚀磨损特征的内弹道模型，拓展了烧蚀磨损内弹道理论。

2) 构建了基于全膛烧蚀磨损特征的内弹道模型的分析解法和数值解法。

3) 以某型火炮烧蚀磨损试验数据为例，利用数值解法进行了内弹道仿真计算，仿真结果与试验结果符合度较好。

4) 本文建立的方法可指导火炮身管寿命内弹道仿真试验。