基于软计算的轻武器装备体系贡献率评估方法

姚天乐， 胡起伟， 齐子元, 温亮， 陶凤和

(1.陆军工程大学石家庄校区 火炮工程系, 河北 石家庄 050003；2.陆军工程大学石家庄校区 装备指挥与管理系, 河北 石家庄 050003)

0 引言

信息化条件下武器装备体系的作战能力具有涌现性，仅靠技术指标的对比叠加难以反映武器装备的实际作战能力。基于此，体系贡献率作为一种全新的评估手段，通过定量计算装备融入装备体系后体系的变化情况，从投入产出的角度全面衡量装备的实际作战能力，是对装备体系作战能力评估的一种有效补充。近年来，研究人员对体系的作战能力进行了一系列探索。齐照辉等[1]提出了基于区间数的多属性决策方法，对导弹突防效能进行了分析评估。王美乂等[2]提出了一种基于模糊信息的熵权多属性方案评估方法，在没有专家权重的情况下得出了可信度较高的优选方案。刁联旺等[3]提出了利用综合命中概率对主战坦克火力能力进行综合分析的方法。陈晨等[4]提出了一种基于数据场站技术的效能评估决策方法，降低了评估数据间的依赖性。在贡献率研究方面，罗小明等[5]提出基于结构方程模型的方法，对武器装备体系贡献度进行了评估。陈小卫等[6]运用复杂系统理论，就新型装备对作战体系的贡献机理问题进行了研究。马亚辉等[7]以协同作战能力为评估标准，提出一种空中预警平台体系贡献率建模方法。陈小卫等[8]在总结现有体系贡献率基本概念基础上，分别给出了基于增量、比值、满意度和费效比的度量方法，指出了其发展方向。综上所述，学者们对体系贡献率评估问题已经做了一些工作，但其中大部分研究是主要针对贡献率概念及作用机理进行的。目前，对于庞大复杂的装备体系，仍然没有准确定量地计算体系贡献率的方法。

本文以步兵轻武器装备体系贡献率评估为背景，提出采用软计算求解体系贡献率的方法。根据武器装备体系具有高度非线性和不确定性、模糊性的特点，按照任务子能力- 体系子能力- 体系总能力的模糊映射链，构造模糊神经网络来求解体系贡献率。这种映射关系的质量通过智能系统的自适应调节实现，充分利用了系统的容错性和鲁棒性，可以适应数据资料的不完整性和专家认识的主观性，发挥软计算在不确定环境中的计算优势，提高贡献率评估的客观性和有效性。

1 基于软计算的体系贡献率评估流程

软计算是近年来出现的建立智能系统的一种新方法[9]，它结合了诸多技术和方法，以解决不确定情况下的实际问题。本文使用的软计算手段结合了遗传算法、模糊聚类和模糊神经网络[10]。首先按照不同的武器能力效用，利用以遗传算法(GA)优化的自组织迭代算法(ISODATA)[11]对轻武器体系中的各武器进行软分类。进而建立任务子能力- 体系子能力- 体系总能力的模糊映射链，并构造相应的模糊神经网络，求解各模糊映射中的贡献率。将两次模糊映射求解的贡献率进行合成，得到任务子能力对体系总能力的体系贡献率。武器体系贡献率评估流程如图1所示。

2 基于效用的轻武器软分类

由于面对任务需求时同种任务子能力在不同武器上发挥的效用不同，对体系子能力的贡献率也不相同，必须按照能力效用对武器体系中的各武器进行分类。软分类的目的是将样本数据划分为不同的类，使同类中的数据具有某种相似性。Bezdek[12]提出的模糊c-均值算法是应用最广泛的算法。由于该算法需要预先定义类别的数量c，但一般在分类前往往并不可能知道c，因此如何获得最佳的分类和相应的最佳聚类数是一个重要问题。本文采用GA-ISODATA，将ISODATA嵌入GA，利用ISODATA的迭代进行最优逼近以实现模糊c-划分，利用GA在整个空间中搜索最佳聚类数以实现武器种类的最佳划分。利用该方法，通过能力效用对轻武器体系中的18种武器进行软分类。

2.1 体系构建与指标选择

以某轻型步兵营步兵轻武器装备体系为研究对象，其结构体系如图2所示。

由于武器装备体系中各级指标之间的关系以及效用的合成关系，借用Cobb-Douglas函数中的投入产出关系，将底层指标看作体系的投入，将高层指标看作体系的输出，以此对各个指标实现聚合。由于Cobb-Douglas函数与时间相关，如果实际产出为Y、输入元素的数量为n，则生产函数的一般形式[13]为

Y=F(x1,x2,…,xn;t)，

(1)

式中：x1，x2，…，xn表示影响产出的n个指标的数值；t表示n个指标导致实际产出Y的时间。(1)式表示输出元素与输入元素之间的某种依赖关系。

为了实现体系中18种武器的软分类，对Cobb-Douglas函数进行如下扩展[14]：

(2)

式中：Y为每种武器的火力支援能力；α、β和γ为常数，α+β+γ=1；A表示每种武器的三元效用，表示每种武器能提供C1、C2和C3共3种能力的百分比，C1、C2和C3分别表示100 m、400 m和1 000 m内的有效毁伤能力。根据(2)式可得

(3)

(3)式表示每种武器的能力效用与该武器的火力支援能力、100 m内有效毁伤能力、400 m内有效毁伤能力和1 000 m内有效毁伤能力具有一定的依存关系。基于这种依存关系，可对步兵营步兵轻武器装备体系中的18种轻武器进行软分类。

2.2 模糊聚类分析

于简氏年刊上查找各轻武器的指标数据，利用效用转化和合成[15]，将各个指标数据转化为各种武器任务子能力的效用值。利用GA-ISODATA对各武器任务子能力的效用值进行模糊聚类，可以得到最佳聚类数c=3. 轻武器软分类隶属度值如表1所示。

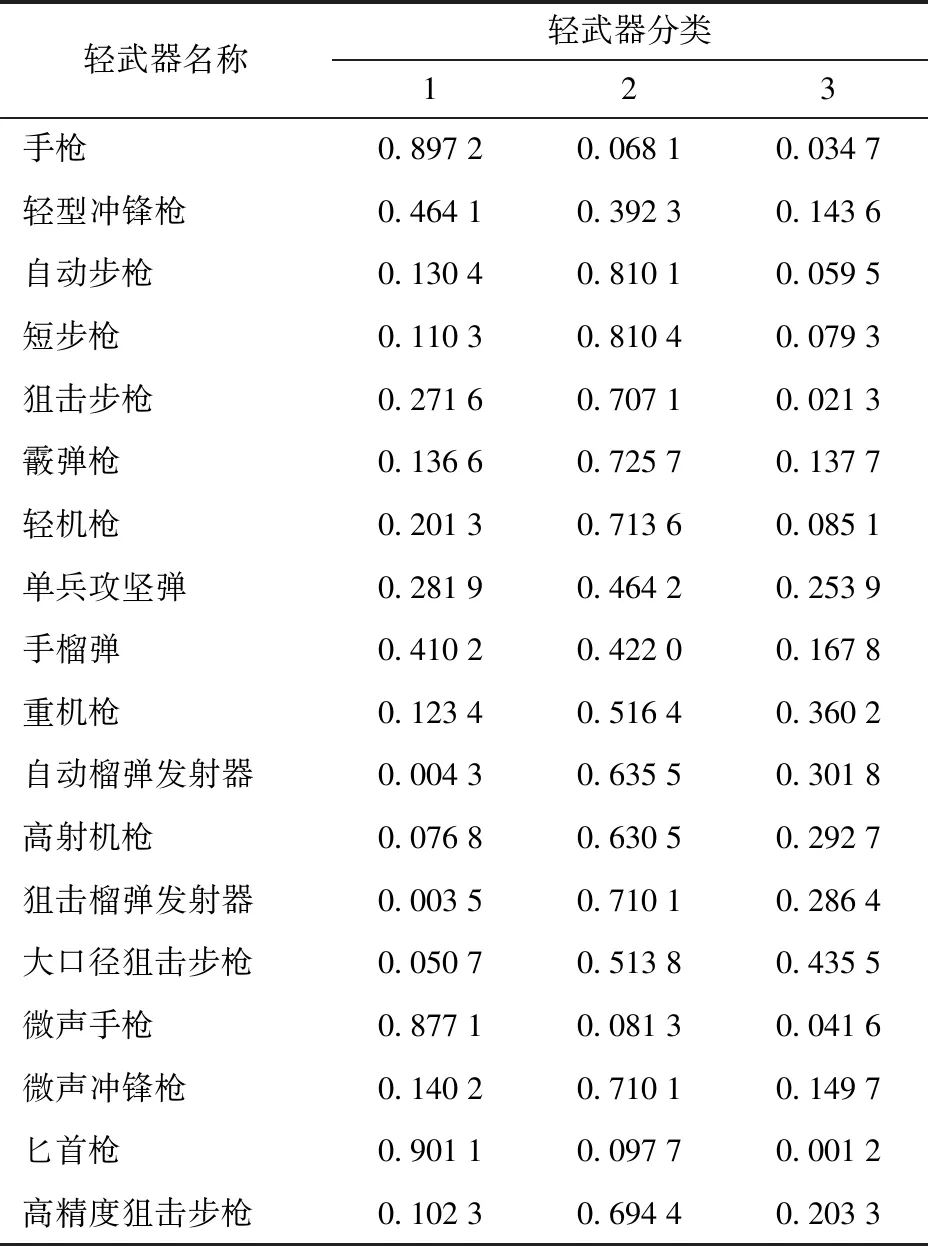
表1 轻武器软分类隶属度表

算法的适应度函数如图3所示，适应度函数的最大点，即分类目标的最小点正好对应于最佳分类数c=3.

根据最大隶属度原则，最佳轻武器软分类结果如表2所示。其中：第1类轻武器表示单兵自卫武器，体积小、射程近、易于携带；第2类轻武器表示单兵战斗武器，射程较远、易于单兵携带；第3类轻武器表示班组支援武器，体积大、射程远、适合班组战斗使用。该分类结果完全符合步兵营轻武器的体系型谱分类特征。

表2 最佳轻武器软分类

3 贡献率评估模糊映射链及映射求解

模糊逻辑利用语言和概念表达大脑的宏观能力，模糊神经网络(FNN)将模糊逻辑嵌入神经网络中，用于处理各种基于隶属函数和一系列规则的模糊信息，具有许多模糊逻辑和神经网络的优点。本文利用3条规则和线性结论构造了体系总能力与体系子能力之间的FNN1映射，以及体系子能力和任务子能力之间的FNN2映射，最终可求解得到体系子能力对体系总能力的贡献率α1以及任务子能力对体系子能力的贡献率α2.

3.1 构建FNN1

如图4所示，步兵轻武器装备体系能力由单兵作战能力、火力支援能力、精确打击能力和特种打击能力组成。

邀请来自论证部门的多位专家对各体系子能力的权重值进行评估，并计算得到各体系子能力的能力值。利用效用转化和合成公式，可以得到体系总能力的效用值。毛义华等[15]提出一种综合各因素的效用转化和效用合成方法，给出效用空间中任意点的总体效用U(u)为

(4)

式中：u为利用效用函数将能力客观值转化而来的效用；wr为由专家主观判断得出的第r个指标的权重；m表示参与聚合的底层指标数；ur表示m个指标中第r个指标能力的效用。在利用(4)式进行效用合成时，两种参数相互作用，既体现了专家在评估时对指标的主观态度，也发挥了指标本身数据的客观作用，因此充分结合了两种方法的优势。将相关数据代入(4)式进行计算，可以得到如表3所示的体系能力效用数值。

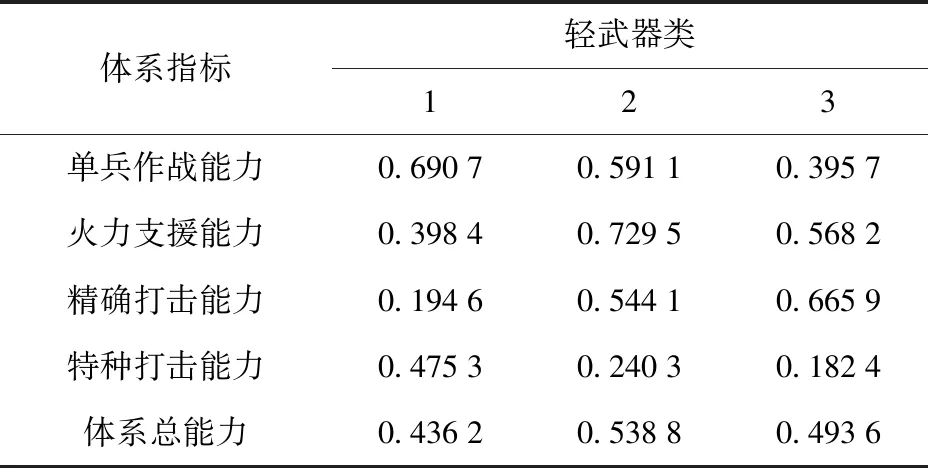
表3 体系能力效用数值表

以火力支援能力对体系总能力的贡献率求解为例，构建FNN1如图5所示。图5中的输入变量x1、x2、x3、x4分别表示4种体系子能力，输出Y表示步兵轻武器装备体系总能力，节点中∑表示求和，∏表示求乘积，f表示求隶属函数，连线处1表示节点间传递、不进行运算。

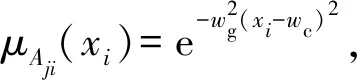
ifx1isAj1andx2isAj2andx3isAj3andx4isAj4,

thenYj=wj0+wj1x1+wj2x2+wj3x3+wj4x4.

本文所构造的FNN1采用反向传播(BP)算法，图5中各层和节点的功能描述如下：

1) δ层：4个节点的输入层，4个节点分别表示输入的4种要素。

2) A层：输入层，共有8个节点，方框中的-1表示固定输入，方框到B层节点的权重为wc，圆圈到B层节点的权重都是1.

3) B层：偏移层，共有12个节点，在节点内作xj-wc的运算；B层和C层之间的权重是wgq，q=1～12.

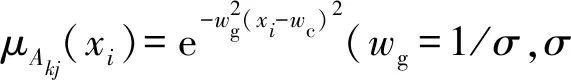
5) D层：合成层，共有12个节点，12个节点的输出为隶属度μAji(xi)；在本层即完成模糊化，D层、E层的权重都是1.

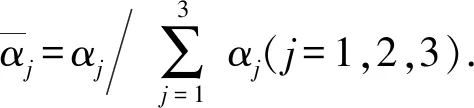
7) F、G、H、I和J层：F层、G层的功能是实现线性函数fk(x1,x2,x3,x4)=wj0+wj1x1+wj2x2+wj3x3+wj4x4. F层中有4个节点，将F层、G层的连接权归一化为ws=1/(x1+x2+x3+x4)。G层有5个节点，G层、H层的连接权重都是1；H层有15个节点；H层、I层的权重是wji，wji同时也表示规则的后件参数；I层有15个节点，I层、J层的权重都是1.

8) K层：K层有3个节点，执行计算：

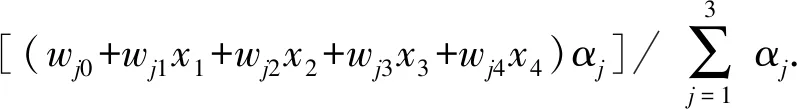
9) L层：解模糊层，仅有1个节点，执行计算

3.2 构建FNN2

体系子能力由各任务子能力组成，包括100 m内毁伤能力、400 m内毁伤能力以及1 000 m内毁伤能力。以400 m内毁伤能力对火力支援能力的贡献率求解为例，可以与构建FNN1同样构建FNN2，从而得到400 m内毁伤能力对火力支援能力的贡献率α2.

按照构造FNN1相似的思路，FNN2中输出与输入间可以写成(5)式结构的函数：

H=f(e,h,s)+ε，

(5)

式中：H表示火力支援能力；e表示100 m内毁伤能力；h表示400 m内毁伤能力；s表示1 000 m内毁伤能力；ε表示随机变量。FNN2的结构和学习算法与FNN1相同。FNN2的输入是100 m内毁伤能力、400 m内毁伤能力以及1 000 m内毁伤能力，输出是火力支援能力。

4 实例分析

为了验证第3节提出的方法，对某山地步兵营轻武器体系400 m内有效毁伤能力对体系总能力的体系贡献率进行评估，作为数值示例。

4.1 FNN1映射结果分析

FNN1的输入是各类武器集群平均单兵作战能力、平均火力支援能力、平均精确打击能力以及平均特种打击能力，输出是平均体系总能力。利用BP算法对FNN1进行训练，可以得到表4所示的3条模糊规则以及各体系子能力的贡献率。表4中S表示后件参数之和。

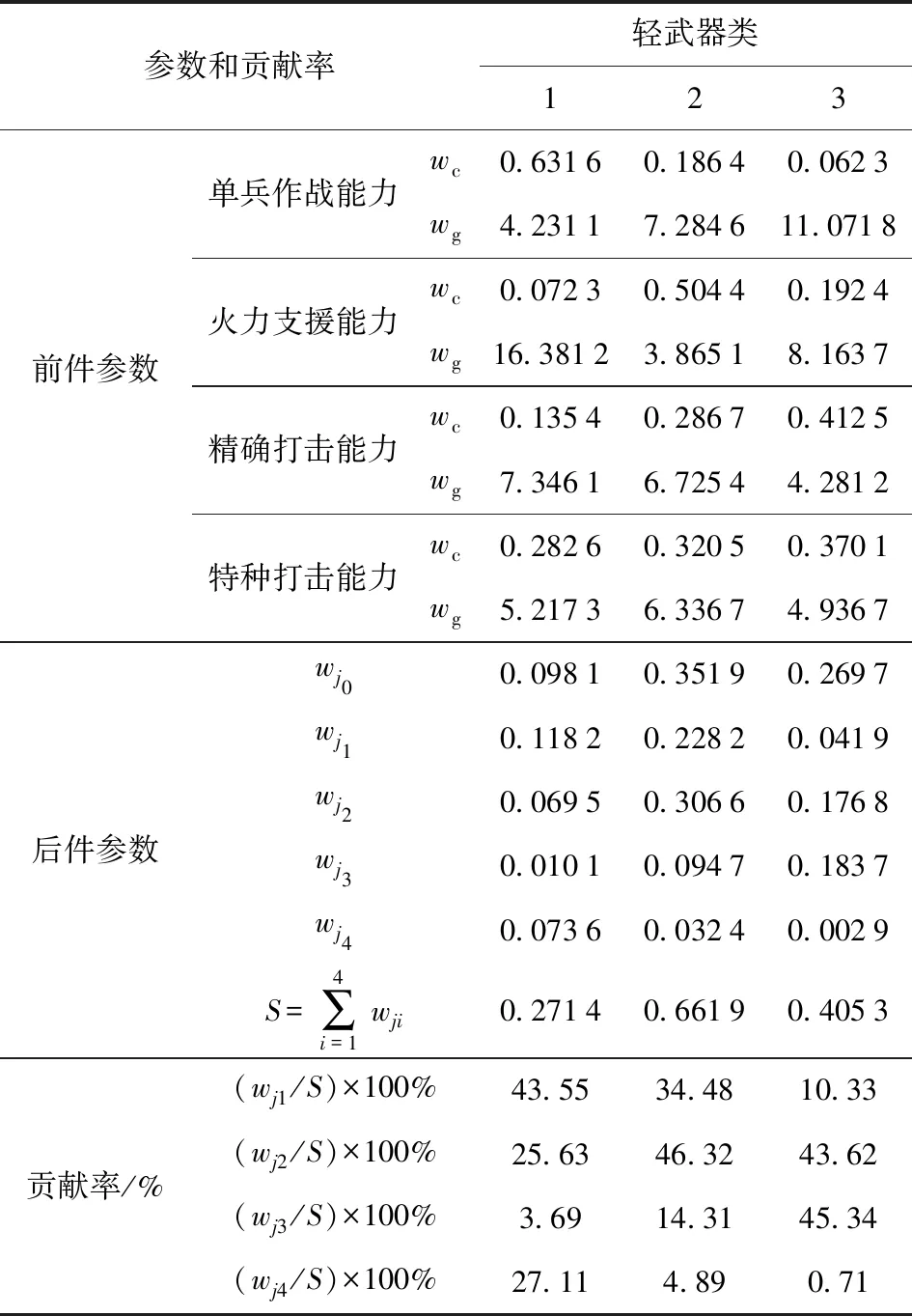
表4 体系子能力的模糊规则及贡献率

通过观察表4中的数据可以看出，在模糊规则前提下，各体系子能力均包含在模糊集中，模糊规则的结果参数由各类轻武器的平均能力组成。在整体平均能力上，显然第2类轻武器优于第3类轻武器，因为w20>w30. 第3类轻武器优于第1类轻武器，因为w30>w10. 第1类轻武器中，单兵作战能力、火力支援能力、精确打击能力以及特种打击能力的体系贡献率分别为43.55%、25.63%、3.69%、27.11%；第2类轻武器中各体系子能力的体系贡献率分别为34.48%、46.32%、14.31%、4.89%；第3类轻武器中各体系子能力的体系贡献率分别为10.33%、43.62%、45.34%、0.71%. 通过比较表4中的数据可知，单兵作战能力与火力支援能力对体系总能力的体系贡献率均比较高；火力支援能力在第2类轻武器中的体系贡献率最高，在第1类轻武器中最低。

4.2 FNN2映射结果分析

利用BP算法对FNN2进行训练，得到表5所示任务子能力的模糊规则及贡献率。

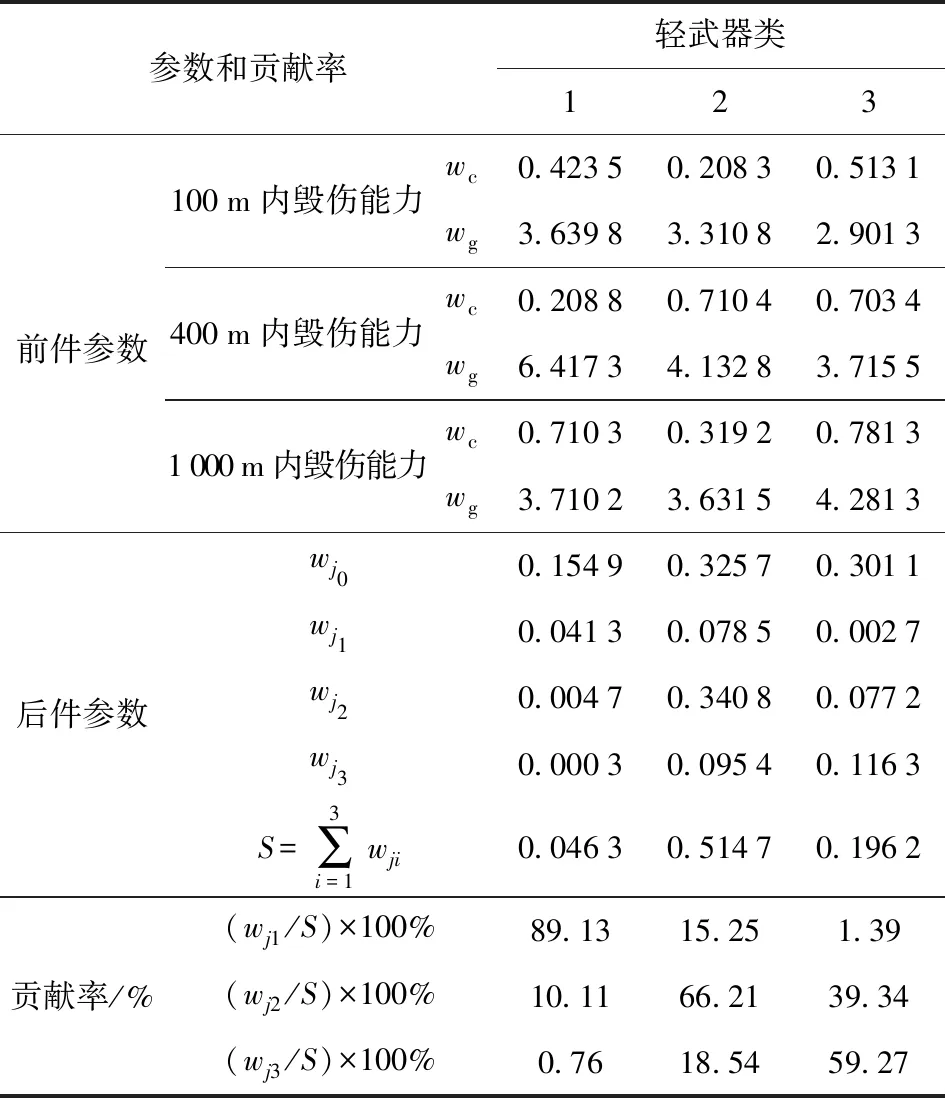
表5 任务子能力的模糊规则及贡献率

观察表5可知，第1类轻武器中100 m内毁伤能力、400 m内毁伤能力、1 000 m内毁伤能力的体系贡献率分别为89.13%、10.11%、0.76%；第2类轻武器中各任务子能力的体系贡献率分别为15.25%、66.21%、18.54%；第3类轻武器中各任务子能力的体系贡献率分别为1.39%、39.34%、59.27%.

4.3 体系贡献率结果分析

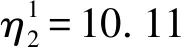
第1类轻武器：

第2类轻武器：

第3类轻武器：

进而可得整个轻武器装备体系中，武器400 m内有效射击能力的平均体系贡献率为η=(η1+η2+η3)/3=16.87%.

各轻武器类及轻武器体系400 m内有效毁伤能力的体系贡献率如表6所示。

表6 各类轻武器400 m内有效毁伤能力体系贡献率

由表6可以看出，不同种类轻武器对轻武器体系总能力的体系贡献率不同。结合表4和表5可以看出，不同种类轻武器具备4种体系子能力的特征并不相同。具体分析如下：

第1类轻武器是单兵自卫武器，射程近、易于携带，主要用于单兵自卫，因此能够提供较大的单兵战斗能力，兼具有火力支援能力。由于第1类轻武器中有微声手枪以及匕首枪等特种作战装备，还具备有特种打击能力。由于单兵自卫武器射程近，基本不具备精确打击能力。第2类轻武器是单兵战斗武器，种类最多、射程较远、较易携带，因此能够提供较大的火力支援能力。大部分第2类轻武器的射程能高于400 m，因此第2类轻武器400 m内有效射击能力对火力支援能力的贡献最高。由于第2类轻武器的单兵战斗能力对体系总能力的贡献可以达到30.67%，第2类轻武器也能提供较强的单兵战斗能力。第3类轻武器是班组支援武器，武器体型较大、射程远，能够提供大量的精确打击能力。第3类轻武器对体系的贡献主要作用于攻击远距离目标，同时对近距离目标也有杀伤作用。分析表4和表5可以看出，第2类轻武器与第3类轻武器均可以提供较大的火力支援能力，但是二者作用目标不同，远距离火力支援能力主要由第3类轻武器提供，400 m内火力支援能力则由第2类轻武器提供。第2类轻武器的精确打击能力相对火力支援能力偏低，如果能有效提高第2类轻武器的射程及精度，则能够有效提高整体的体系总能力。

5 结论

本文针对轻武器装备体系具有高度非线性、不确定性和模糊性等特点，提出了基于模糊数学和神经网络的软计算来量化体系贡献率的方法。采用模糊聚类方法对轻武器体系中的武器进行软分类，利用模糊映射链求解了各模糊映射中的贡献率。本文贡献及主要结论如下：

1) 构造的模糊映射链较好地契合了轻武器装备体系递阶层次结构，使能力指标体系最底层元素对顶层元素的贡献率也能实现精确求解。在本文基础上，面对更复杂的装备体系可以建立更长的模糊映射链来求解体系贡献率，为其他种类武器装备体系贡献率评估提供了一种新思路。

2) 模糊神经网络有效地适应了数据资料的不完整性和专家认识的主观性，发挥了软计算在不确定环境中的计算优势，提高了贡献率评估的客观性和有效性。

3) 通过对各类轻武器底层能力对上层能力的贡献率计算，能够更清楚地了解各类轻武器的优势与弱势，为轻武器装备体系结构优化提供依据，为计算轻武器装备融入体系后体系的变化情况提供了一定的参考。